球面与简单多面体表面交线问题探究

魏东升

(福建省厦门双十中学漳州校区 363107)

在最近笔者所在学校年级组织的一次高三月考中，一道立体几何的问题引起了笔者关注．因为其得分情况几乎可以用“惨不忍睹”来形容，即便是笔者所在的层次较好的班，其情况也不容乐观．经过对试题进行深入探究发现，这个问题是立体几何中的一种经典问题，其解法亦具有普遍性．

1 真题再现

本题选自2020年新高考山东卷的第16题．从考查知识方面来说，主要考查了立体几何点线面位置关系，简单几何体的构造，轨迹问题和扇形的弧长公式等；从考查知识方面来说，主要考查了数形结合思想，转化与化归思想和整体与局部思想等；从考查能力方面来说，本题主要考查了学生的直观想象能力，数学抽象能力和数学运算能力等，很好地体现了《考试说明》中强调的“以能力立意，强化对数学学科核心素养的考查”.作为填空压轴题，有很好的区分度，具有较好的选拔功能．

2 本质呈现

这类问题其实是几何中的截弧问题，属于球“切截接”(球内切问题，球截面问题和球外接问题)中截面问题的一种，其上次出现还是在2007年全国高中数学联赛中.所谓截弧，是指平面中的圆(或圆弧)被直线或线段所截，或者是空间中的球被多面体(或平面图形)所截，所得截线是一个圆或是一段圆弧，但常常是圆弧居多，实际上其和麻将这类益智类游戏中的“截和”有异曲同工之妙.

解决这类问题的关键是需要具备解题的整体思想，能够直观想象到多面体截得的弧是圆的一部分，同时结合已知条件通过数学运算获得该圆的圆心和半径，进而得到圆弧所在扇形的圆心角.

如果球面与几何体的某个表面有交线，则球的半径应该大于球心到该面的距离，且小于球心到该面内点的最大距离.在实际问题中，不管是准确作出交线的轨迹还是计算轨迹的长度，都绕不开弧心(即轨迹所在圆的圆心)的确定，由图1可知，弧心其实就是球心O在截面上的投影A.弧心的确定可以分为三类：弧心即球心；弧心在边界及弧心在面内.以下结合实例分析这三种类型的解题策略.

图1

3 类型展现

3.1 弧心即球心

如果球面与球心所在面相交，则其交线所在圆即为大圆，该截弧的弧心即为球心.

例1 已知正三棱台ABC-A1B1C1的上下底边长分别为2和5，侧棱长为3.以下底边顶点A为球心，2为半径的球面与正三棱台的表面的交线长为____.

图2

解析如图2，因为球A的半径为2，所以其只与正三棱台的表面A1B1BA，A1C1CA及ABC等三个面相交.假设其与这三个面的交线的交点分别为点D，E，F.因为球心A刚好在这三个面内，所以球心A也就是对应截面圆的圆心，其与正三棱台的交线也就是以A为弧心的三段弧长．

评析本题解题的关键是确定球和多面体的几个表面有交线．由于球的半径小于球心到面A1B1C1和面B1C1CB的距离，所以其只与球心A所在的三个面有交线，而点A也就成了这三段截弧的弧心.

3.2 弧心在边界

如果球心所在面与截面垂直，则该截弧的弧心必在两个平面的交线上．

图3

评析注意到点A1所在的两个平面A1B1BA及A1B1C1D1同时和平面BB1C1C垂直，所以点A1在平面BB1C1C的投影即为这三个平面的公共点B1.所以点B1就成了平面BB1C1C所在截弧的弧心.

3.3 弧心在面内

如果球心所在面与截面不垂直，则该截弧的弧心必在截面的面内．

例3 已知正四面体ABCD的棱长为2．以BC的中点E为球心，1为半径的球面与该正四面体的右侧面ACD的交线长为____．

图4

解析如图4，因为球心A1不在面ACD内，所以需要找到其在这个面的投影，也就是截面圆的圆心．

取AD的中点M，连接BM和CM，易证得平面ACD⊥平面BCM，所以球心E在面ACD的投影G刚好落在平面ACD和平面BCM的交线CM上．

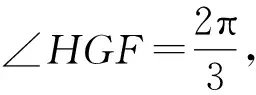
评析事实上，很多时候会碰到截弧的弧心出现在所截面的面内的情况，这个时候需要找到一个垂面，即过球心且和截面垂直的平面，此时可知弧心会出现在这两个平面的交线上．

有了以上知识储备，我们再来看看这道真题的解析．

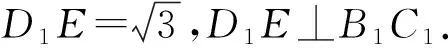
图5

设P为侧面B1C1CB与球面的交线上的点，

则D1E⊥EP.

需要指出的是，在解题时上述类型的运用往往并不一定是孤立的，可能会是多种情况同时出现，这一点可以通过改变多面体的类型，变换球心的位置或者球的半径得到，而这也是数学命题中一题多变的思想源泉．