三种求解含参数方程的常规思路

马雪峰

(山西省临汾市洪洞县第一中学校 041600)

1 直线参数方程几何意义求解

在题干部分明确AB距离的情况下，可以反推直线方程的表达式.

分析求解参数方程有关问题，即可直接利用直线参数方程的几何性质进行解答：首先分别求出直线l和圆C的极坐标方程，在极坐标方程中有关弦长可以利用|ρ1-ρ2|进行求解，即可得到有关直线l的斜率tanα的方程，最后解方程便可求得直线斜率.

解析根据题意可得C的极坐标方程为ρ2+12ρcosα+11=0，直线l的极坐标方程为θ=α.

设A,B两点对应的极径分别为ρ1,ρ2，

将直线的极坐标方程θ=α

代入C的极坐标方程ρ2+12ρcosα+11=0中，

则有ρ1+ρ2=-12cosα，ρ1·ρ2=11.

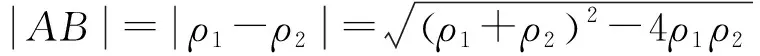
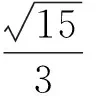
2 数形结合法求解

数形结合求解参数方程，具体是把参数方程表示的直线或曲线图象描绘在直角坐标系中，然后通过图象位置关系的变化找到满足题意要求的参数所需条件，根据这个特殊位置的关系，进而得出参数的取值范围.

分析解答该问题，直接求解的解题思路和过程较为复杂冗长，不妨考虑利用数形结合方法求解，把曲线N与曲线M的极坐标方程化为直角坐标方程，然后画出相对应的图象，通过移动图象求t的取值范围.

图1

①当曲线N在直线l1的位置时，与曲线M只有1个公共点；

②曲线N从直线l2位置平移到直线l3的过程中，也与曲线M只有1个公共点，

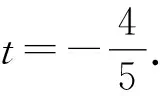
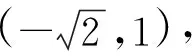
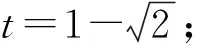
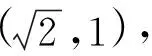
3 联立直线与圆锥曲线方程求解

已知含参数直线方程解析式l，曲线方程表达式C，求直线l与曲线相交AB距离问题时，可以通过将圆锥曲线一般方程变换为参数方程，再通过将直线l方程的代入求出相关参数关系.

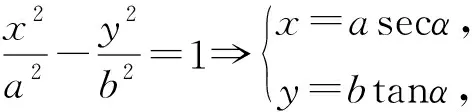
通过联立含参数方程求出t1+t2，t1t2的数值，进而转化成求AB距离.

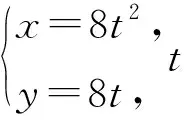
解析由题意，得l:2x+y-4=0，C：y2=8x.

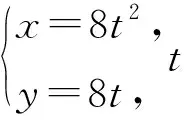
将C代入l,得4t2+2t-1=0.

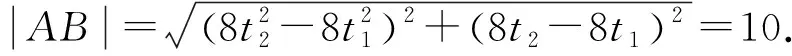
总之，这些方法都是同学们必须掌握的有效解答参数问题的方法，也是同学们应该思考和总结其中解题关键和有关思想的解题方法.只有熟练掌握这些常见的解法，才能帮助同学们更快速高效地解答参数方程问题.