基于ANSYS Workbench的机械臂模态分析及振动控制
李飞伟
(国网嘉善县供电有限公司, 浙江, 嘉善 314100)
0 引言
三坐标定位机械臂被广泛应用于振动环境下低压电器的可靠性检测。由于车辆行驶过程中不平整度以及动力设备运行引起的载荷,导致机械臂一直处于振动环境中,在这种复杂的环境下容易产生振动疲劳破坏,导致结构失稳[1-3]。因此,对三坐标定位机械臂进行振动分析对于开展低压电器可靠性检测具有实际工程意义。近些年来,NASTRAN、ANSYS以及ADAMS等有限元软件为机械结构在动力学分析、结构尺寸参数灵敏度以及优化设计方面提供了更方便快捷的计算方式[4-5]。通过功能强大的分析软件对机械臂开展振动特性、运动特性分析,获得机械臂接近实际情况的受力特点[6],对存在的设计问题进行针对性的优化设计,同时避免由于动载荷作用下产生振动效应造成的机械臂结构疲劳破坏[7]。基于此,本文在相关研究的基础上,采用ANSYS WORKBENCH分析软件进行机械臂的动态特性分析,获得机械盘振动特性的固有频率和相应振型,基于获得的模态分析结果,给出机械臂在典型工况下的谐振特性。
1 带电检测机械臂模态分析
1.1 模型建立
本文低电压检测机械臂主要用来对电压电气进行定位,通过机械臂上装设的抓取机构抓低压电气触头,进行可靠性参数检测。该机械臂主要包括驱动电机、涡轮蜗杆减速器、丝杠导轨、水平工作台以及固定支架组成。其中丝杠导轨主要实现X、Y、Z3个坐标向的定位和移动,并由相应的电机提供驱动动力,固定支撑主要是便于机械臂对电压电气定位和安装机械臂,蜗轮蜗杆减速器主要增加转矩,将电机转速降低到驱动转速,图1为整个检测机械臂的正视图。
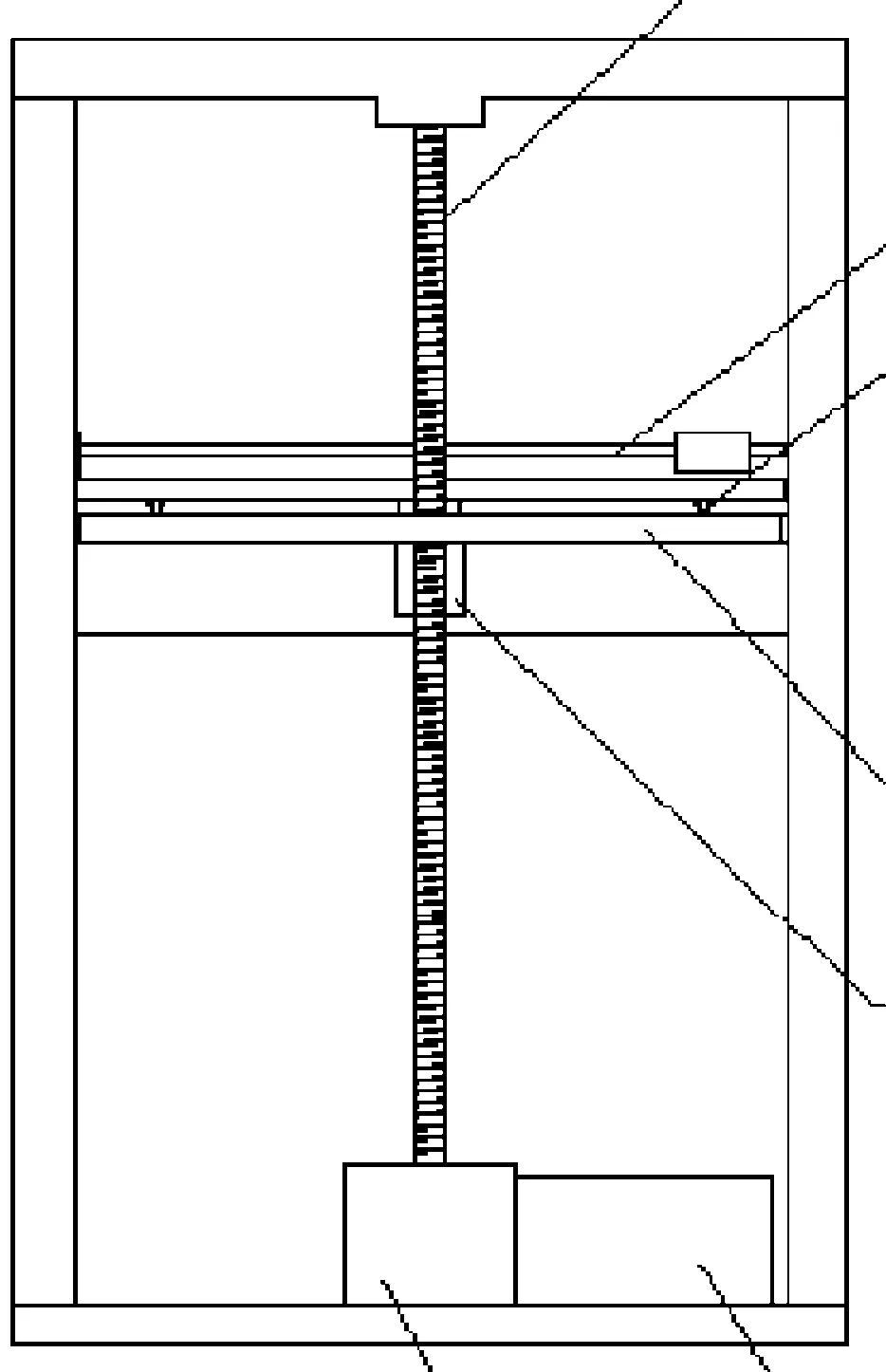
图1 电压电器检测机械臂结构图
1.2 机械臂的有限元建模
采用ANSYS Workbench分析软件对机械臂的模态特性进行分析,首先在CAD软件中建立实体模型,在建立CAD的机械臂模型时,根据实际情况对机械臂进行了部分简化:删除尺寸较小的倒角、圆角和螺栓,对模型中的小锥度、小曲率曲面进行平面化处理,对涡轮涡杠减速器和驱动电机简化为实际相符的长方体,图2为通过CAD软件建立的简化模型图。

图2 简化的机械臂结构图
将建立的模型导入到ANSYS Workbench分析软件中,对模型进行网格划分。考虑到计算内存大小以及计算速度和准确度,本文采用多种网格划分方式,对涡轮涡杠减速器与丝杠连接处、与电机连接处以及螺纹与光杆分割边线,采用映射面网格划分方式,进行适当加密。对机械臂导轨、电机、外部框架等,进行网格控制,设定网格单元尺寸大小为5 mm,其余结构部件进行自由网格划分,如图3为机构网格划分效果,整个机械臂共划分为350 993个节点,108 353个单元数。

图3 三坐标定位机械臂的有限元模型
2 机械臂的振动特性分析
2.1 机械臂的静力分析
本节首先对机械臂在典型工况下的应力值和位移值进行静力学分析,判断机械臂在正常工况下是否满足强度要求。机械臂在工作中,受到的载荷主要为X向丝杆导轨上抓取机构拉动触头的抓取力,由于实际工作中最大不超过200 N,因此,在X向抓取机构位置施加200 N的静载荷,并对机械臂底部施加固定约束,为便于分析,将典型工况进行数字简化,表1中为机械臂各部件工况和代号。

表1 机械臂各部件和工况代号
根据表1中不同的工作平台和工作位置,确定12种典型工况,通过有限元模型对12种工况进行静力分析,获得各工况下的最大位移和应力水平如表2所示。
由表1中可以看出,在工况11时获得的等效位移和应力最大,即工作台位于框架中部,X向丝杠滑块位于丝杠中部,X向丝杠位于y向丝杠中部。因此确定工况11时机械臂的不稳定工况,获得相应的位于云图和应力云图如图4所示,可以看出,机械臂最大位移量达到了0.41 mm,最大应力值为52.78 MPa,远低于材料屈服极限250 MPa,因此,极限工况下不会对机械臂的强度造成影响,整个检测机械臂强度满足要求。
2.2 机械臂模态分析
机械臂模态分析可以确定结构的固有动力学特性,通过模态分析,获得模态振型下结构各部位在某阶固有频率的相对位移量,了解系统薄弱环节,并有针对性性提升结构的抗振能力。根据上节机械臂各工况下的静力学分析结果获得的最不稳定工况,开展对该工况下的模态分析。由于固有频率只与材料弹性模量、泊松比和边界条件有关,外部载荷影响相对较小,因此在建立模态分析模型时,只需要在建立的静态模型下将框架底面固定,不需要加载外部荷载,仅施加一个Fixed support 即可。
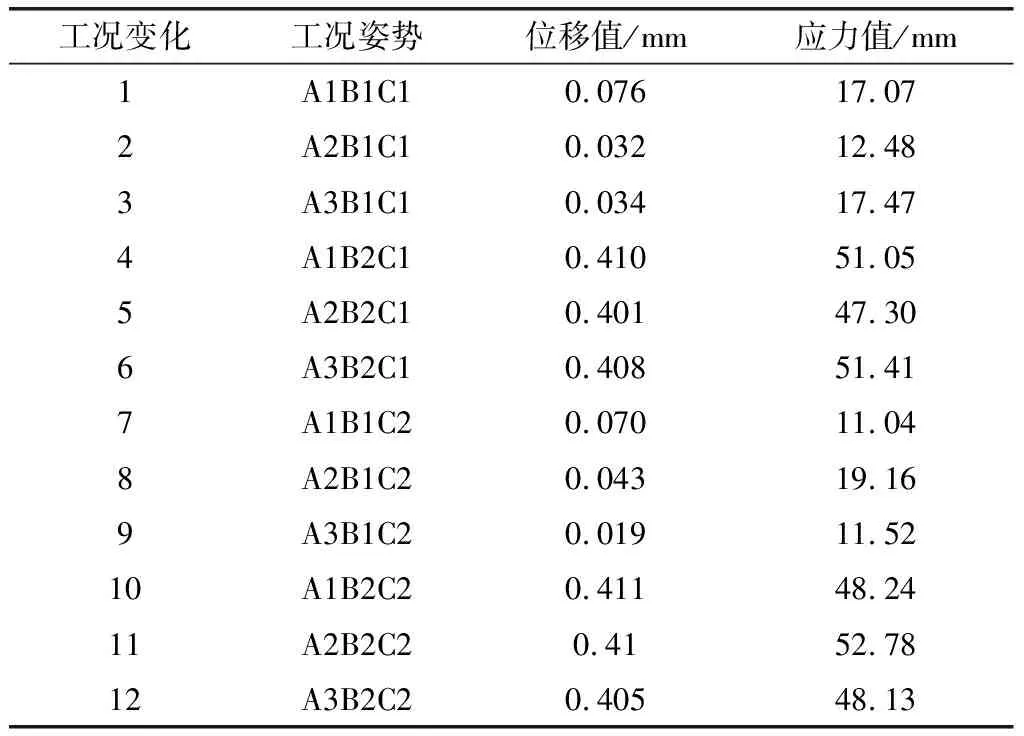
表2 机械臂典型工况下的位移和应力值

(a) 应力云图 (b) 位移云图
实际应用中,尽管机械臂有无限自由度,相应的模态存在无限阶。但低阶模态频率和刚度相对较低,在相同激励下的前几阶模态相应占比最大。因此,本文主要对机械臂前10阶模型进行分析,图5为获得的前10阶固有频率和振型云图。

图5 机械臂前十阶振型云图
由图5可知,机械臂的前六阶主要为框架的振动变形,且在前三阶以y、Z向的框架扭转变形为主,对应的固有频率分别为49.69 Hz、54.29 Hz、65.88 Hz,第4—6阶以框架弯曲振型为主,其中第4阶振型以框架立柱与z轴丝杠沿y向弯曲,第5阶以框架立柱与轴丝杠在x向弯曲,第六阶以立柱在x、y向弯曲,相邻立柱弯曲相反。第4—6阶的固有频率分别为144.33 Hz、163.93 Hz、210.48 Hz。第7阶振型以立柱在水平工作台上方向不同向弯曲为主,第8阶振型为x轴向2根横梁、z轴丝杠向y轴弯曲,第9阶时未连接z轴丝杠的衡量向z向弯曲且相连立柱向x向弯曲,第7—9阶的固有频率分别为237.66 Hz、342.18 Hz、360.37 Hz。第10阶整个机械臂形成局部振动,水平工作台和x轴向丝杠向z向摆动,固有频率为405.26 Hz。
通过比较模态分析可以看出,机械臂前3阶模拟振型结果与实际观察振型相同。由于前6阶振型主要是框架结构沿x、y向的弯曲振动和摆动,表明该框架结构在x、y向存在刚度不足的问题,比较第4阶、第5阶振型主要以x向丝杠和导轨的弯曲变形为主,表明丝杠和导轨在y、z向存在刚度不足的问题,因此,可以对框架进行优化。
2.3 机械臂的谐响应分析
通过模态分析获得机械臂固有频率和相应振型,但模态分析更多的是表示机械臂各部位相对振动情况,而实际工作环境中,机械臂在外界激振力作用下的频率范围和实际振型是不相同的,因此对机械臂外界激振力下的实际动态响应,有利于减少可能存在的失效。
本节在机械臂安装抓取机构位置添加x、y、z向幅值为200 N的简谐力,设定频率范围为10—410 Hz,求解步长为100,相位角0,图6为机械臂在施加简谐力作用下抓取机构位移相应曲线。

图6 机械臂谐振响应结果
由图6中可以看出,在机械臂安装抓取机构施加简谐力时,在52 Hz、142 Hz、406 Hz的固有频率下的机构位移达到最大值,比较x、y、z3个方向下机械臂在简谐力的位移相应可知,安装抓取机构在x轴向简谐力作用下的位移达到做大,最大位移量为0.475,在y轴向简谐力作用下的位移为0.432 mm,而z轴向简谐力下的位移最大值为0.386 mm。比较模态分析下的机械臂固有频率,对应最大位移量下的固有频率分别为第2阶固有频率54.29 Hz,第4阶固有频率143.33 Hz,第10阶固有频率405.26 Hz接近,表明在外界机理作用下,机械臂在第2、4、10模态更易于被激发,且在第2阶达到位移最大响应值。综合比较谐分析和模态分析结果可以看出,第2阶振型为框架在z向的刚度较低,导致框架结构发生摆动,在第4阶振型框架向x向弯曲,由于第10阶固有频率已经远远超过机械臂工作频率范围,因此忽略其影响。
3 总结
本文在有限元法、模态分析和谐响应分析基础上,利用ANSYS Workbench软件建立了低压电气检测机械臂的三维有限元模型,对机械臂在典型工况下的静力学和振动特性响应特性进行分析,确定机械臂结构在谐振型的结构稳定性,研究获得的主要结论如下。
(1) 当工作台位于框架中部,X向丝杠滑块位于丝杠中部,X向丝杠位于y向丝杠中部时,机械臂处于不稳定工况状态,机械臂最大位移量达到了0.41 mm,最大应力值为52.78 MPa,低于材料屈服极限250 MPa,检测机械臂强度满足要求。
(2) 模态分析下的机械臂前3阶模拟振型结果与实际观察振型相同。谐响应条件下,机械臂在第2、4、10模态更易于被激发,且在第2阶达到位移最大响应值,安装抓取机构在x轴向最大响应位移量为0.475 mm。

