基于博弈论和云模型的通用机场选址方案评价

杨昌其， 郝铭佟， 付熙文

(中国民用航空飞行学院， 空中交通管理学院， 四川， 广汉 618307)

0 引言

近几年，我国通用机场的建设规模呈逐步扩大的趋势，通用机场的建设对区域发展至关重要，我国在通用机场选址方面的政策也越来越严格，因此，机场的场址位置如何选择便是一个关键问题。我国机场的选址过程一般分为初选、预选和比选3个阶段，最终形成优选方案。许多专家在选址方案的决策问题上先后进行了深入的研究。刘光辉[1]对充电站的选址问题进行了研究，提出了基于云模型和PROMETHEE评价法的评价模型；邓波尔等[2]构建了客运站的选址评价体系，利用集对分析法，同时考虑了选址过程中指标的差异性和重要性，并选取实例进行了验证；陈俊峰[3]以TOPSIS法为核心建立了一种水上机场选址的评价模型，并将模型应用到实际过程中进行了选址决策; Lee YG等[4]建立了一种基于用户均衡的位置模型来进行选择决策；Juan CM等[5]以费用最小为目标建立了一种博弈模型来分析枢纽机场的位置与邻近机场的竞争关系。

为了解决通用机场选址决策过程中的问题，首先需要建立一套适用于通用机场选址方案评价的指标体系，然后确定各指标的权重值，根据专家对各方案、各指标的打分情况求得对应的云模型参数，再与标准云模型形成对比，分析得出最终的最优化方案，本文的整体流程如图1所示。

1 评价指标体系的构建

基于通用机场选址要求，综合考虑通用机场使用特点，按照多方案评价指标体系设置原则，以机场选址方案最优化为评价目标，经比较和总结，寻求专家意见选取了多个比较重要的评估指标，将建设条件、运行条件、综合交通条件、外部保障资源条件、可承受经济条件、敏感条件设置为一级指标，并根据对通用机场选址方案评价指标体系的研究分析，在一级指标下下设22个二级指标，整体指标体系如图2所示。

图1 整体流程图

图1中准则层为U,一级指标为B={B1,B2,…,B6}，二级指标为C={C11,C12,…,C63}，方案集为D={D1,D2,…,Dn}。

2 权重集化模型的构建

2.1 基于G1法确定指标的主观权重

G1法[6]是在层次分析法(Analytic Hierarchy Process，AHP)方法的基础上改进的一种主观权重的赋值方法，AHP法的核心是构造判断矩阵,而判断矩阵存在一致性问题，G1法较好的解决了这一问题，在确定各指标权重过程中不需要构造矩阵，计算过程更为简便。

G1法步骤如下。

① 确定评价指标的序,对指标集x1,x2，…，xn>中的元素进行比较得到关系式(1)：

图2 通用机场选址方案评价指标体系

x1>x2>，…，>xn

(1)

就是在评价指标x1,x2，…，xn>之间确立了按“>”排序的序关系。

② 邀请专家对评价指标xk-1与xk相对于准则层的重要程度进行比较，得出重要程度之比式(2)：

Wk-1/Wk=rk(k=n,n-1，…，3,2)

(2)

即WK-1的权重是Wk的rk倍，其中rk的参考值见表1。

表1 rk赋值参考表

③ 计算得出权重系数。基于以上2步，即可求出指标的主观权重:

(3)

Wk-1=rkWk(k=n,n-1，…，3,2)

(4)

2.2 基于熵权法确定指标的客观权重

熵权法[7]以指标的变异性来确定指标的权重，用来衡量某一指标对目标值的影响。指标所对应的熵值决定着指标内在的信息量，同时也决定着指标的权重大小，熵值与信息量之间呈负相关关系，而信息量与权重之间呈正相关关系。

熵权法计算权重的步骤如下。

① 设m个评价对象和n个评价指标中的第i个对象的第j个指标取值为xij，构造原始评价指标数据矩阵式(5)：

X=(xij)m×n

(5)

② 对矩阵X进行数据归一化处理。

对越大越优的指标有式(6)：

(6)

对越小越优的指标有式(7)：

(7)

③ 求各指标的信息熵。一组数据的信息熵式(8)：

(8)

式中

(9)

如果Pij=0，则定义lnPij=0。

④ 确定各指标权重。通过信息熵计算各指标的权重式(10)：

(10)

2.3 基于博弈论原理的组合赋权法

为了增加模型的客观性，使评价结果更符合客观事实，引入博弈论的综合赋权法，在主观权重的基础上，融合客观权重，该方法实现了多方法赋权过程中的纳什均衡。其核心思想是尽可能的减少由于不同的赋权法所导致的指标权重的不统一，从而提高所得权重的准确性，减少主、客观权重之间的冲突。

为使所得出的最终权重(即基本指标权重)与各方法下所求得的权重偏差最小，达到多种权重下的纳什均衡，需要形成指标权重集，构建博弈论集化模型。

由多种赋权方法分别求得的彼此独立的指标权重向量被称为基本指标权重，由多个基本指标权重任意的进行线性组合之后所得到的集合被称为指标权重集，由n个基本指标权重向量的任意线性组合可记为式(11)：

(11)

为使w与各个wi的离差极小化，得到更优的指标权重向量w*，对式(11)中的系数αi进行优化，决策模型如式(12)：

(12)

由式(12)可知，为了得到最优的综合权重值，我们将多目标函数进行最优化处理后对上式进行求解，然后通过对矩阵的微分性质进行分析，得到该决策模型的最优化一阶导数条件为式(13)：

(13)

其对应于下面的线性方程组式(14)：

(14)

3 云模型的构建

云模型是李德毅教授提出的一种不确定性定量与定性互换模型[8]。该模型可以考虑到评价过程中的随机性和不确定性，同时评价指标既能含有定性指标，也可以含有定量指标，一定程度上减小了主观因素对评价结果的影响，使评价结果更科学有效。

云是用期望Ex、熵En、超熵He来描述的，Ex是指期望，En是指定性部分的可度量粒度，He是熵的熵，由熵的随机性和模糊性决定[8]。

3.1 云模型的表示

指标的初始值由分值或某一具体数值确定，评分值由专家们按同一标准进行打分得出，然后利用逆向云发生器求出各指标对应的云模型数字特征(Ex，En，He)。

二级评价指标基本上互相独立、相互不影响，因此通过二级评价指标云模型参数进行一级评价指标的综合云的计算运用如下计算公式：

(15)

式(15)中，n为评价指标的总个数(i=1，2，…，n)，Wi为第i个二级指标的权重，Exi为第i个二级指标的期望，Eni为第i个二级指标的熵，Hei为第i个二级指标的超熵。

一级指标与二级指标相比，指标之间的关联性更强，因此对最高层指标进行评价时，需要进行虚拟云中的综合云运算，其计算方法如式(16)：

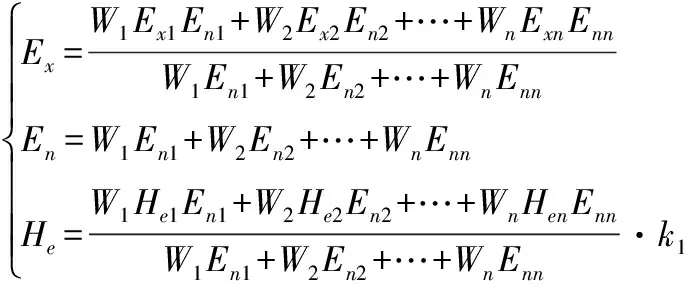
(16)

式中，n是评价指标个数(i=1，2，…，n)，Wi为第i个一级指标的权重，Exi为第i个一级指标的期望，Eni为第i个一级指标的熵，Hei为第i个一级指标的超熵，k1取常数，可以根据几个云模型图的可区分程度进行调整，取值在0-1之间。

3.2 指标体系评语集

确定各级指标的评语，形成评价集。其中I级和X级属于单边约束[Cmin，Cmax]，其余属于双边约束。对于双边约束的评语，可通过式(17)求出云模型的数字特征：

(17)

式中，k2取常数，由变量的不确定性决定，取值在0-1之间。

该算法中的具体指标的评分等级和其对应的云模型如表2所示，为了便于理解和计算，专家评价的分值范围为0到100；为了得到一张云滴离散程度不太大，又不至于太过集中符合实际情况的标准云模型图，经过对比测试，决定将k2取值为0.5。结合云模型计算步骤和表2，由MATLAB运行得到图3。

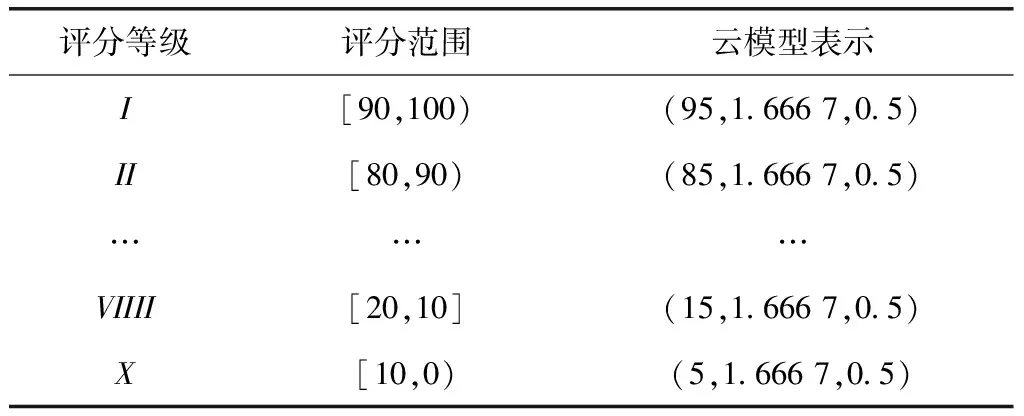
表2 评分等级及其云模型表示

图3 标准云模型图

4 实例分析

现以国内某一已建通用机场为例进行验证分析，基于机场选址方案的实际评估指标(见图2)，采用G1法、熵权法，综合考虑指标权重的主客观性，尽可能克服定性指标评价的主观性和随机性的缺点，对云模型进行调整后再做评价，流程图如图1所示。

4.1 确定指标权重

应用2.1中提到的算法，代入式(3)和式(4)进行计算后，得到一级指标和二级指标的权重系数如表3和表4所示。

表3 一级指标G1法权重

表4 二级指标G1法权重

应用2.2中提到的算法，代入式(5)到式(10)进行计算后，得到一级指标和二级指标的权重系数如表5和表6所示。

将表2-表5中的基本权重向量wi分别代入式(13)，得权向量的集化模型式(17)：

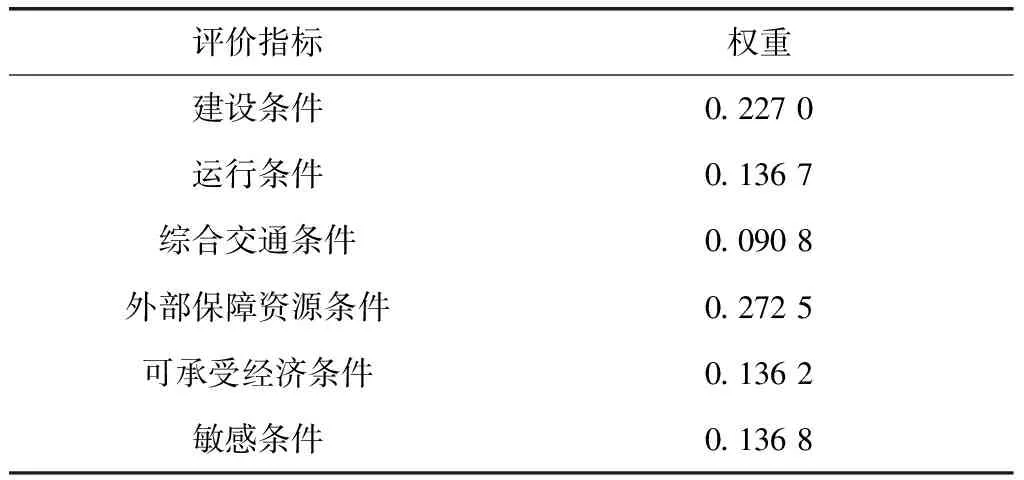
表5 一级指标熵权法权重

表6 二级指标熵权法权重

(18)

利用计算机求解式(18)得：α1=0.986 5，α2=0.042 6

则最满意权重向量w*的系数：α*=(0.986 5，0.042 6)。

由式(11)可求得最优权重解为：

4.2 云模型验证

根据式(15)和式(16)计算得出通用机场选址方案综合评价结果的云参数依次为(77.173 4，3.826 1，0.626 2))，(78.931 6，7.670 6，1.332 0)，(78.772 0，4.497 8，0.976 8)，(81.062 5，9.080 1，1.401 8)，(85.299 6，3.676 3，0.655 8)。

为了与评价等级标准云图相比较，各方案云的厚度，即超熵He要适中，云滴的离散程度既不能太大也不能太小，才具有区分度，因此，取云滴数500个，k1值均取为0.5，生成结果云图，如图4-图8所示，可以分析得出下述结论。

以国内某一通用机场选址过程中的5个初选场址评价结果分析为例。由最大隶属度原则可判断，方案1的场址等级属于III级，偏向于II级；方案2的场址等级属于III级，偏向于II级；方案3的场址等级属于III级，偏向于II级；方案4的场址等级属于II级，偏向于III级；方案5的场址等级属于II级。

从云滴分布情况分析(图4—图8)，方案2和方案4的熵值En较大，所以分布较为分散，方案3的云滴聚合程度与方案1和方案5相比较差，方案5与方案1图形的整体情况较好，但方案5的均值Ex略优于方案1，因此,选取方案5为优先方案。

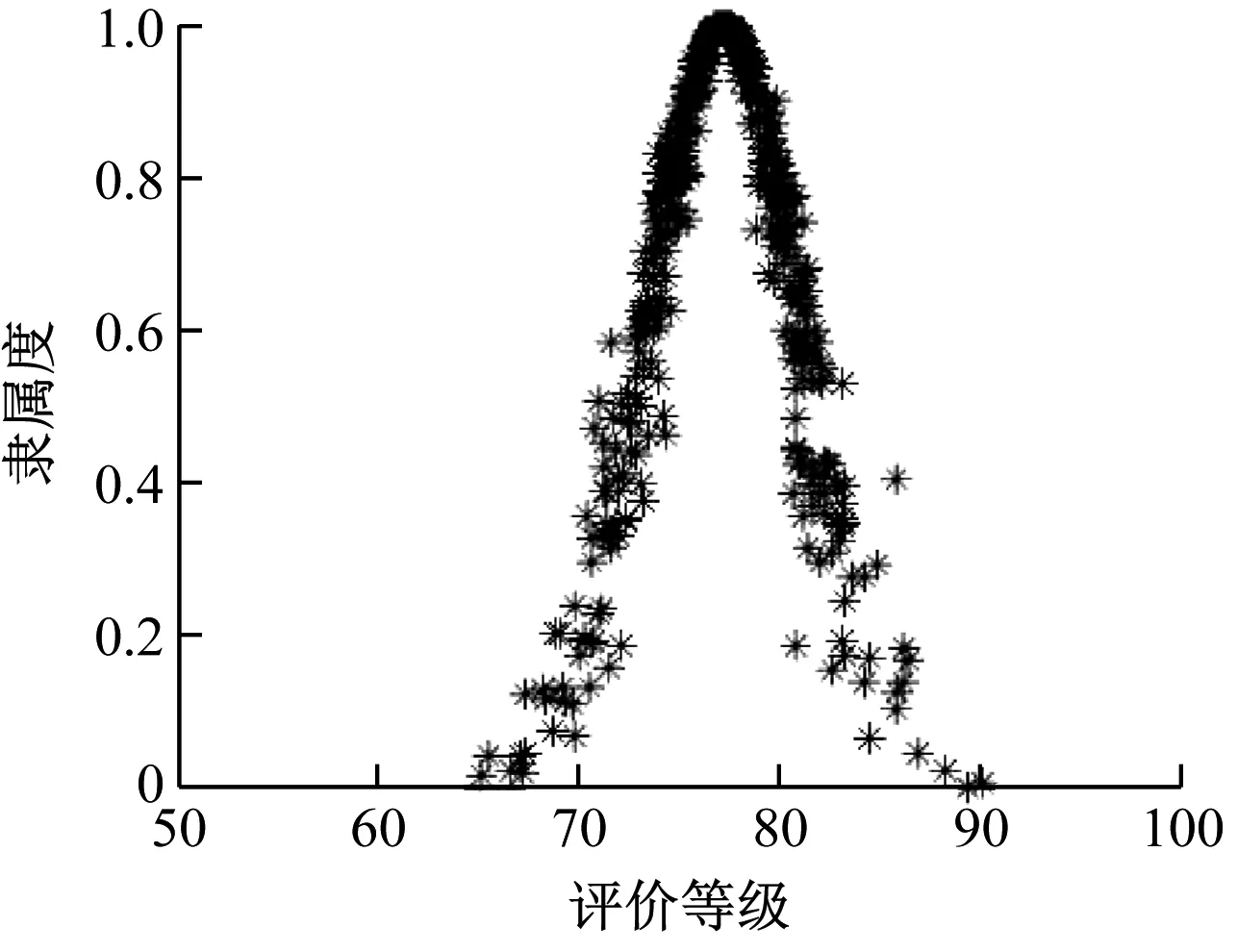
图4 方案1云模型图

图5 方案2云模型图

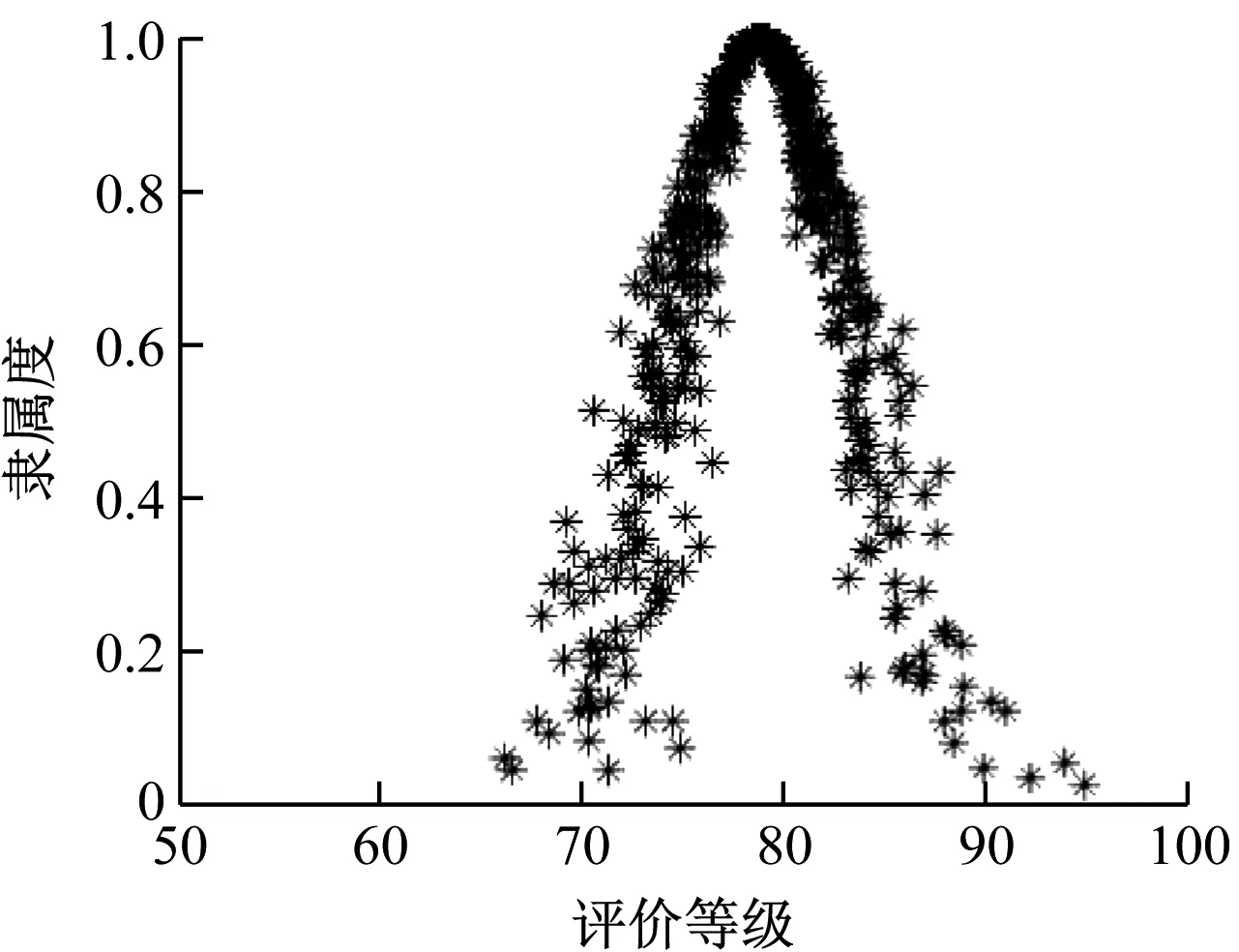
图6 方案3云模型图

图7 方案4云模型图

对上述5个通用机场的初选方案进行评价后，可以分析得出方案5为最优方案。另外，在实际选址过程中决策者们通过分析得出的最优方案也是方案5。这一相同的结论也证明通过本文所述方法建立的通用机场选址方案评价模型在实际应用中是可行的。

图8 方案5云模型图

5 总结

针对通用机场选址方案的评价问题，本文首先构建了更加符合实际的通用机场选址方案评价指标体系；其次选取G1法确定主观权重，选取熵权法确定客观权重，利用博弈论组合赋权法对各级指标进行了赋权，达到了主、客观权重下的纳什均衡，并构建了符合通用机场选址的云模型，充分考虑了评价过程中的模糊性和随意性；最后，通过实例分析验证了本文所构建的通用机场选址模型的有效性，同时验证了该方法在通用机场选址时进行决策辅助更加简便、快捷，评价结果具有客观性、直观性和科学性。