用柯西不等式及其一个推论解题

甘志国

(北京丰台二中 100071)

≥(a1b1+a2b2+…+anbn)2，

当且仅当bi=0(i=1,2,…,n)或存在一个常数k使得ai=kbi(i=1,2,…,n)时等号成立.

推论(权方和不等式)若x1,x2,…,xn∈R,y1,y2,…,yn∈R+,n≥2，则

1 求最值

解法1 设x=a+5(x>5),y=b+3(y>3)，

可得a=x-5,b=y-3,x+y=11.

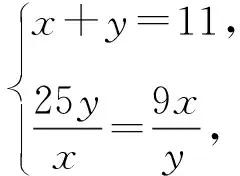
解法2 由题设及推论，可得

题2 (2017年全国高中数学联赛广西赛区预赛试卷第8题)过半径为5的球面上一点P作三条两两互相垂直的弦PA,PB,PC使得PA=2PB，则PA+PB+PC的最大值为____.

解析可得以PA,PB,PC为共顶点的三条棱的长方体内接于球，且该长方体的体对角线长为球的直径，所以PA2+PB2+PC2=(2×5)2,5PB2+PC2=100.

再由推论，可得

题3已知实数a,b,c,d满足a+b+c+d=3,a2+2b2+3c2+6d2=5，求a的最大值和最小值.

解析由题设及柯西不等式，可得

≥(b+c+d)2，

当且仅当2b=3c=6d时取等号.

即5-a2≥(3-a)2，解得1≤a≤2.

进而可得，

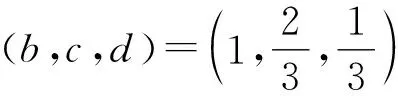
所以a的最大值和最小值分别是2，1.

解析由柯西不等式，可得

=40,

解析由柯西不等式，可得

当且仅当x-6=31-x，

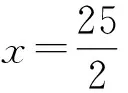
解析由推论，可得

进而可得，当且仅当a1=a2=…=a2017=1时，

2 求值

解析由推论及均值不等式，可得

即x=y=2，进而可得x+y=4.

解析由推论，可得

3 证明不等式

证明可得a2+b2≥2ab,a2+c2≥2ac,a2+d2≥2ad,b2+c2≥2bc,b2+d2≥2bd,c2+d2≥2cd.

把它们相加后，可得

3(a2+b2+c2+d2)

≥2(ab+ac+ad+bc+bd+cd).

故3(a+b+c+d)2

≥8(ab+ac+ad+bc+bd+cd).

0<4(ab+ac+ad+bc+bd+cd)

再由推论，可得

≥(a+b+c+d)2/[a(b+2c+3d)+b(c+2d+3a)+c(d+2a+3b)+d(a+2b+3c)]

证明由推论，可得

证明由推论，可得

=x1+x2+…+xn.

题12 (第24届(1983年)IMO试题第6题)设a,b,c是某个三角形的三边长，求证：a2b(a-b)+b2c(b-c)+c2a(c-a)≥0，并给出等号成立的条件.

图1

证明如图1所示，作△ABC的内切圆，可得从点A出发的两切线长均相等，设为x；点B出发的两切线长均相等，设为y；点C出发的两切线长均相等，设为z，则

a=y+z,b=z+x,c=x+y.

所以要证不等式等价于

(y+z)2(z+x)(y-x)+(z+x)2(x+y)(z-y)+(x+y)2(y+z)(x-z)≥0.

即xy3+yz3+zx3≥xyz(x+y+z).

再由(1)的解答可得该不等式成立，且(2)中的不等式取等号的充要条件是a=b=c.

证明由推论，可得

题14求证：

(1)若a1,a2,…,an是正的实常数，a0,p,q是实常数，x0,x1,…,xn是实变数，且满足

则x0的取值范围是

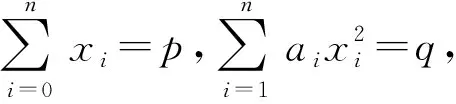
(3)(Laguerre不等式)若

证明(1)由题设及柯西不等式，可得

当且仅当a1x1=a2x2=…=anxn时取等号.

进而可得欲证结论成立.

(2)由(1)可得.

=n(p2-2q)-2q,

所以p2≤(p2-2q)(n+1)，再由(1)的结论可得欲证结论成立.