巧用反比例函数k的几何意义模型解题

黄秋燕

(福建省晋江市第五中学 362200)

教师在解题教学时应当注重发展学生的数感、符号意识、几何直观、推理能力和模型思想，通过让学生体会模型的发现，探讨模型的解题思路，把数形结合思想及参数意识贯穿于解题过程，以此教会学生运用数学思维方式进行思考，促进其应用能力的提升，从而培养学生的数学素养和综合能力.下面主要谈谈反比例函数k的几何意义的各类模型及其它们的简单应用.

1 反比例函数面积不变形模型(k的几何意义)

结论1：S矩形ABEO=S矩形DOFC=|k|;

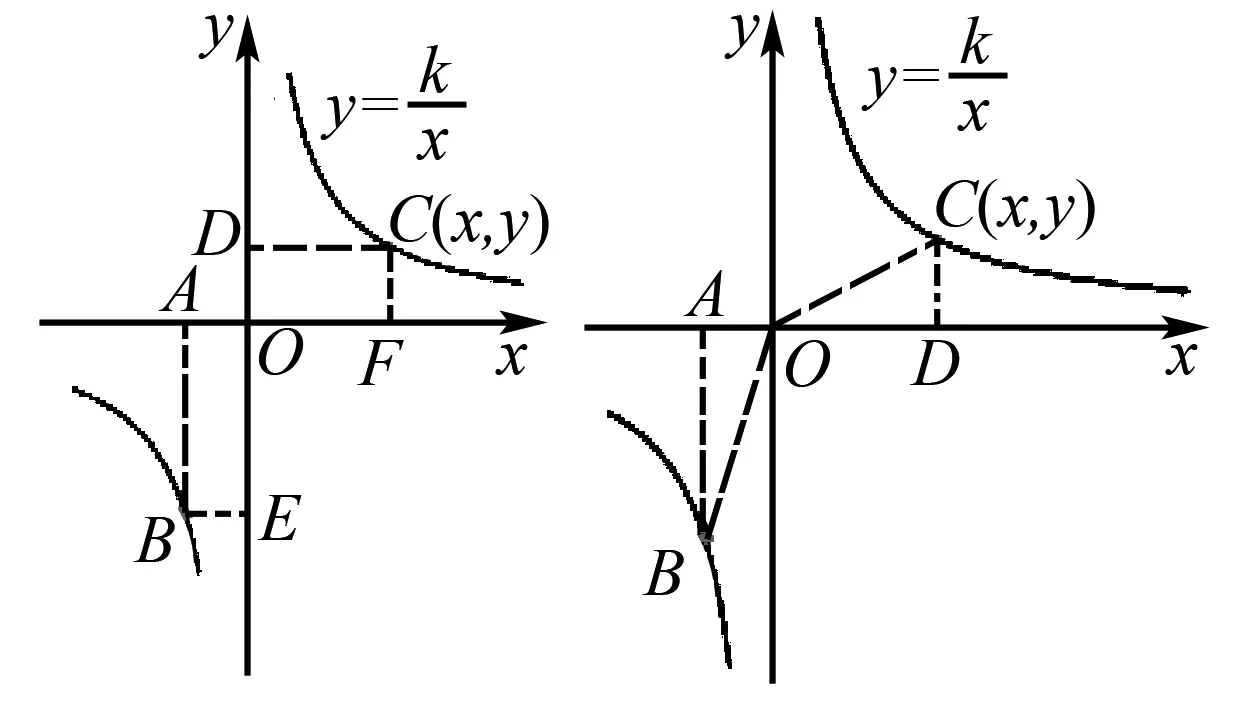
图1

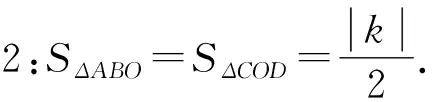
2 反比例函数的面积公式模型

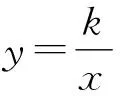
结论3：SΔABO=S梯形AMNB(如图2)

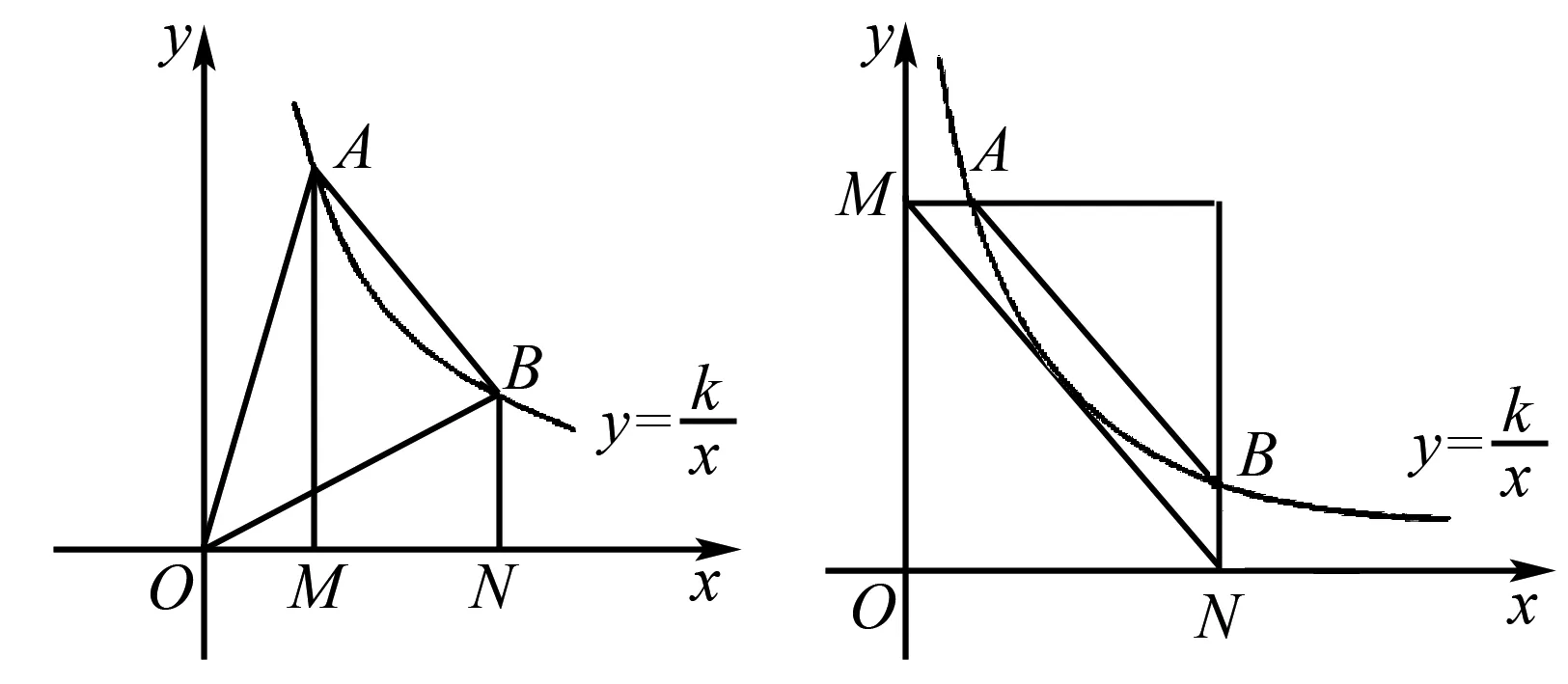
图2 图3

3 反比例函数的平行性质模型

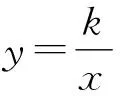
结论4：过点A、B分别作x轴、y轴的垂线，则AB//MN.(如图3)

4 反比例函数等线段性质模型

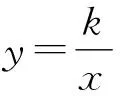
结论5：过点A、B作直线与坐标轴分别交于M、N两点，则AM=BN.(如图4,5)

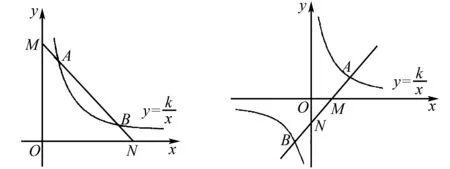
图4 图5

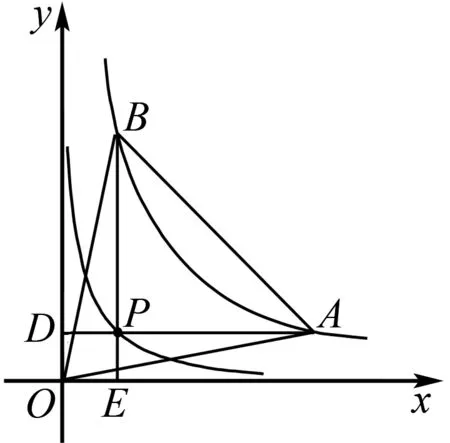
图6

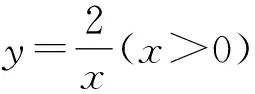
(1)求k的值；

(2)连接OA，OB.若点P的横坐标为2，求△AOB的面积；

(3)若直线AB分别与x轴，y轴交于点M，N，求证：AM=BN.

(2)过点A作AF⊥x轴于点F，过点B作BE⊥x轴于点E.

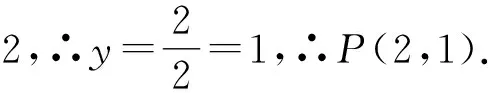
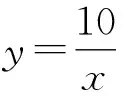
∴SΔAOF=SΔBOE=5.(此步运用反比例函数的面积不变形模型的结论2可得)

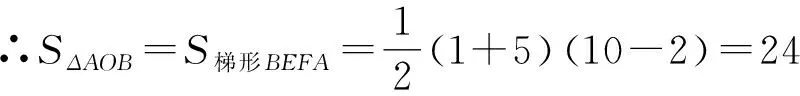
(3)此题是一般方法，过点B作BG⊥y轴于点G.

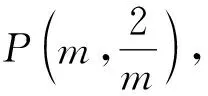
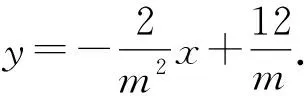
FM=OM-OF=6m-5m=m，

∵∠NGB=∠AFM=90°，

∴△NGB≌△AFM，∴AM=BN.

解法二：先求得SΔNOB=SΔAOM，再利用等高得到AM=BN；

解法三：在RtΔNGB和RtΔAFM中，利用勾股定理求得AM=BN.

【解后反思】本题考查反比例函数的模型应用，考查学生的数形结合、几何直观、推理能力、模型思想等，体现初中数学课程标准中，“用数学符号建立方程和函数的数量关系和变化规律”.

5 反比例函数之同侧双曲模型

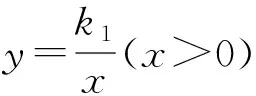
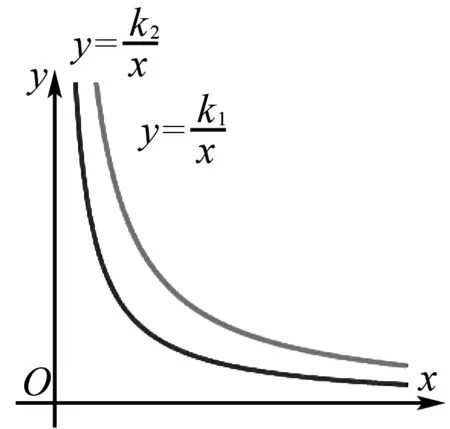
图7

结论6:S矩形ABNP=|k1-k2|(如图8，9).

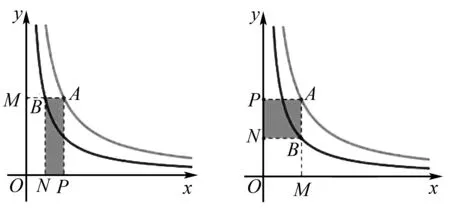
图8 图9

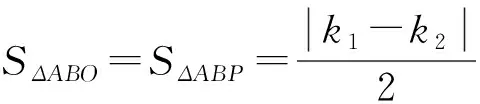
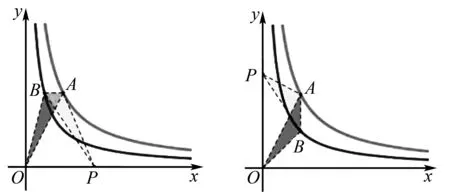
图10 图11

6 反比例函数之异侧双曲模型

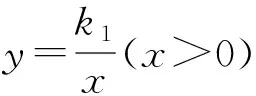
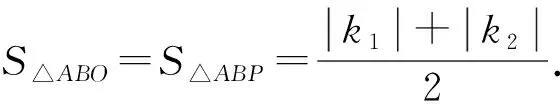
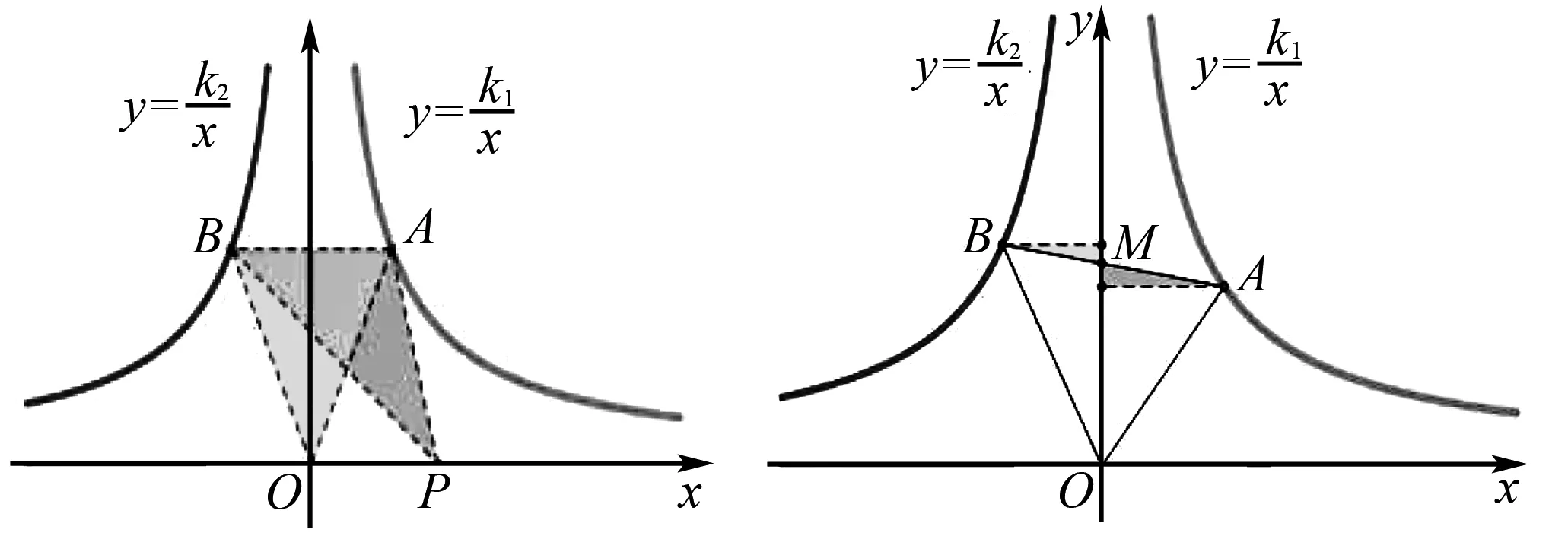
图12 图13

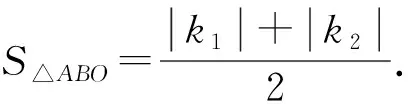
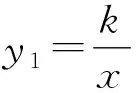
A.2 B.4 C.6 D.8

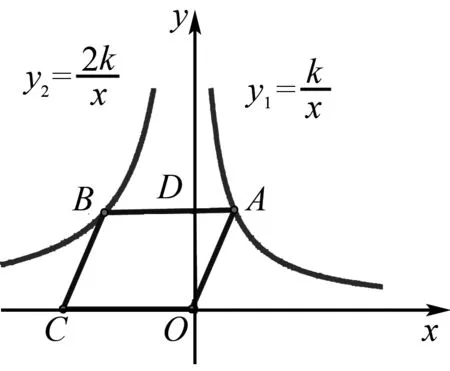
图14

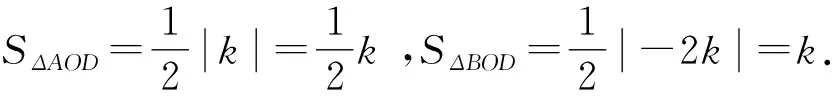
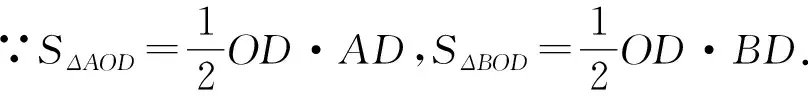
可得BD=2AD,

又∵四边形ABCD是菱形，∴AB=OA.

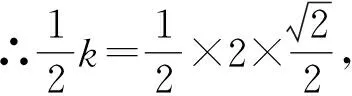
总之，基于以上六类模型的总结和类型例题的讲解，学生可以通过对模型的熟悉和掌握，得出解题的技巧，从而帮助学生解决此类问题做到得心应手.我们在教学中应该重视这些模型的掌握和应用.