一类分数阶捕食-食饵模型的Hopf分岔分析

江 位，周 文

(1.安徽师范大学 数学与统计学院,安徽 芜湖 241000;2.安徽大学 大数据与统计学院，安徽 芜湖 230000)

分数阶微分方程模型非常重要,受到诸多学者的青睐,已经取得了一系列研究成果[1]。宋萍等[2]探索和讨论了一类具有捕获的分数阶种群捕食模型,并明确地指出分数阶导数阶数不但直接影响到该系统收敛到平衡点的速度,而且还影响系统的稳定性。黄承代[3]研究了一类分数阶神经网络模型,并且以分数阶阶数α和系统参数A作为分岔参数,分别考察了分数阶网络的稳定性和Hopf分岔的影响机制,并且给出了相应的发生分岔的条件。田晶磊[4]通过深入细致地研究4个分数阶群捕食者-食饵模型,给出了两类系统的平衡点稳定性和分岔性质的一系列结论。其他学者[5-11]也深入地探讨了各种分数阶系统模型,并得出了一系列具有重要意义的结论。

在真实的生态种群系统中,时滞效应常常影响种群的密度分布,如妊娠。而具有时滞效应的分数阶微分系统稳定性的理论分析和数值模拟的研究较少。因此,本文将讨论一类分数阶捕食-食饵模型的正平衡点的局部渐近稳定的条件,以及发生Hopf分岔时的条件,最后通过数值模拟来验证讨论的结果。

1 模型的建立和Hopf分岔分析

本文研究以下具有时滞的分数阶捕食系统:

(1)

式中，u(t)、v(t)分别表示在t时刻食饵和捕食者的密度。s、β、h、ρ、α、γ、m均为正常数；s为捕食者对食饵的捕食率；β为捕食者对食饵的最大摄入比率；h为对食饵的非线性捕获系数；ρ为半饱和系数；α为捕食者的增长率；γ为在浮游生物死亡的背景下,由于自我保护而导致的光衰减系数；m为对捕食者的捕获系数。初始条件u(s)=μ(s)>0,s∈[-τ,0],v(0)=v0>0,且μ(s)是光滑函数,q1、q2是分数导数的阶数。

定义1[12]函数f(t)的q阶Caputo分数阶导数定义为

(2)

式中，m=[q]是一个整数,Γ(·)是Gamma函数。

引理1[12]考虑以下n维分数阶系统:

(3)

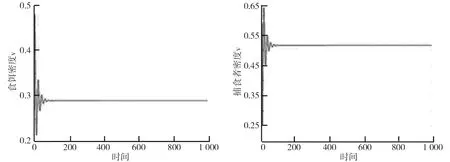
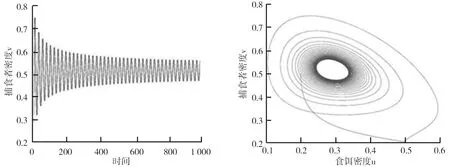
式中，0

在生态意义上,我们只考虑系统的正平衡点E(u*,v*),下面我们对正平衡点的存在性进行讨论，首先假定ρ>h，

令Dq1u(t)=0,Dq2v(t)=0,可得：

(4)

(5)

su*(αu*-mβ-mu*)·(ρ+u*)=0。

整理后可以得出u*是四次方程f(u)=A0·u4+A1·u3+A2·u2+A3·u+A4=0(*)的根(舍去u*=0)，其中,系数A0、A1、A2、A3、A4如下所示：

A0=-mγ,

A1=(1-ρ)mγ-(α+2m)βγ,

A2=(α+2m)(1-ρ)βγ+(ρ-h)mγ-(α+m)β2γ+(m-α)s,

A3=(α+m)(1-ρ)β2γ+(α+2m)βργ+(ρ+β)sm-(2m+αh)βγ-αsρ,

A4=smρβ+(α+m)(ρ-h)β2γ。

又因为当ρ>h时,f(0)=smρβ+(α+m)(ρ-h)β2γ>0。则由介值定理便可得,至少存在一点u*∈(0,+∞)使得f(u*)=0。

下面给出正平衡点的存在性定理,我们提出假设：

(H1)αu*-mβ-mu*>0,ρ>h。

定理1若(H1)成立,系统至少有一个正平衡点E(u*,v*)。

综上,至少有一个正平衡点E(u*,v*)存在。

在正平衡点E(u*,v*)处式(1)相对应的线性化系统定义为

Dq1u(t)=a11u(t)+a12v(t)

Dq2v(t)=a21u(t)+a22v(t)+b21u(t-τ)，

(6)

为了讨论式(1)局部稳定性的情况,对式(6)的两端进行拉普拉斯变换：

(7)

这里,U(s)、V(s)是u(t)、v(t)在经过U(s)=L(u(t)),V(s)=L(v(t))后的拉普拉斯变换。因此,式(7)的特征矩阵为

(8)

令|Δ(s)|=0,可得式(1)的特征方程为

p1(s)+p2(s)e-sτ=0,

(9)

其中p2(s),p1(s)如下所示:

p2(s)=-a12b21,p1(s)=sq1+q2-a22sq1-a11sq2+a11a22。

(iw)q1+q2-a22(iw)q1-a11(iw)q2+a11a22-a12b21e-iwτ=0

分离实部和虚部得:

(10)

式中，参数F1、E1、F2、E2如下所示:

F1=0,E1=-a12b21,

由式(10)我们可以得到:

(11)

显然有sin2wτ+cos2wτ=1,因此可以得到:

(12)

再根据coswτ=f1(w)求得:

(13)

为了分析当τ=0时式(1)的稳定性,提出假设：

(H2)a11≤0。

定理2当τ=0时,若(H2)成立,则式(1)的正平衡点E(u*,v*)是渐近稳定的。

证明当时滞τ=0时,可以得到式(1)的特征方程为

λ2-(a11+a22)λ+a11a22-a12b21=0,

(14)

假设式(12)至少具有一个正实根w0,定义分岔点为τ0=min{τ(k)},k=0,1,2,…。同时为了得到本文的重要结论,提出如下的假设：

其中，

证明为了验证Hopf分岔横截性条件,对特征式(9)的两端关于时滞τ进行求导可得：

化简得：

再由前面假设的

可以得到:

因此,(H3)表明横截性条件是满足的。

定理4若(H1)～(H3)成立,则对于式(1),可以得出如下结论:

①正平衡点E(u*,v*)在τ∈[0,τ0)时渐近稳定;②当τ=τ0时,式(1)在正平衡点E(u*,v*)处会发生Hopf分岔。

2 数值模拟

使用Matlab对系统进行数值模拟,验证时滞对正平衡点E(u*,v*)的影响。选取参数值如下:

β=0.45,ρ=1,γ=1.05,s=0.85,h=0.15,α=1.25,m=0.05,q1=0.9,q2=0.76。

计算得正平衡点E(u*,v*)=(0.289 9,0.516 9),τ=4.084 8。我们分别取τ=2.5<τ0和τ=4.1>τ0进行数值模拟。

系统在τ=2.5<τ0时,食饵u(t)、捕食者v(t)的密度随时间变化的演变图分别如图1、2所示。从图1、2中可以看出,u(t)和v(t)最终趋于正平衡点。τ=2.5<τ0时的稳定相图如图3所示。从图3可以看出,正平衡点E(u*,v*)是局部渐近稳定的。

系统在τ=4.1>τ0时,食饵u(t)、捕食者v(t)的密度随时间变化的演变图如图4、5所示。由图4、5可以看出，随着时间的演化其密度是振荡的,因此正平衡点E(u*,v*)不是稳定点。对应的相图如图6所示。从图6也可以看出，正平衡点是不稳定的，在其外部存在一个极限环。

图1 食饵密度随时间变化的演变图 图2 捕食者密度随时间变化的演变图

图3 τ=2.5<τ0时稳定相图 图4 食饵密度随时间变化的演变图

图5 捕食者密度随时间变化的演变图 图6 τ=4.1>τ0时不稳定相图

3 结论

本文研究了一类分数阶捕食-食饵模型。首先给出了系统的正平衡点的局部渐近稳定的条件,然后讨论了发生Hopf分岔的条件,通过数值模拟验证了理论结果。研究结果表明，时滞的加入会影响到正平衡点的稳定性。