品味物理概念

安 宇

(清华大学 物理系,北京 100084)

物理学中经常有一些说法，语义比较清楚，但其中含义并不是容易理解的.这类说法有很多，比如有人会说：在超导体中，因为规范对称性被破坏，所以光子的静止质量不为零.其含义不容易理解，是因为前提和结论之间的联系并不是很直接.要真正理解这句话，需要仔细剖析细节，建立明显的因果联系.还有一些说法在教材中很少解释，比如布朗运动中爱因斯坦扩散系数.爱因斯坦研究布朗运动取得了重要成果，这是广为人知的，但这里与布朗运动有关的系数为什么加上了扩散两字，有关它的解释是通常教科书中不太常见的.因为教学中这类概念不多见，很多学生也不太关心，所以很多教师也并不太在意.但是少数有志于物理研究的优秀学生有可能在学习过程中触及到这些概念，有机会就相关问题与任课教师讨论，因此有责任感的物理教师有必要深入理解这些概念，挖掘其含义，以备不时之需.

本文梳理出了几个有趣的话题做仔细分析，由此更深入理解相关的物理概念.

1 爱因斯坦扩散系数

布朗运动的研究结果对物理学的发展产生了深刻影响.有很多方法研究布朗运动，比较直观的方法是郎之万模型[1]，他假设质量为m的布朗粒子受到随机力F的作用，在阻力系数为γ的黏性流体中运动.为了简单我们考虑一维情形(三维情形没有本质区别)：

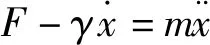
(1)

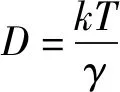
爱因斯坦研究布朗运动是利用无规行走模型. 一维无规行走，要么前行，要么后退，概率都是50%，相当于扔硬币，正面朝上向前迈步，背面朝上向后退步. 假设平均步长为l， 平均迈一步需要时长τ，则迈了N步后，向前n步，向后N-n步的概率为

(2)

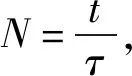
进一步来讲，爱因斯坦认为扩散实际是粒子无规行走的结果，等同于布朗运动. 考虑在原点初始时有n0个粒子，这些粒子在一维液体中扩散,则t时刻在x位置发现粒子的数目等于布朗粒子此刻无规行走到此处的概率乘以粒子数，即n0PN(n). 当N很大时，利用式(2)近似得到

利用D、x、t替换N、m，得到

(3)

实际上，扩散问题可通过扩散方程直接求解：

(4)

其中ρ是扩散粒子数密度，D*是扩散系数. 对于原点初始有n0个粒子的扩散问题，有解析解[2]为

(5)

与式(3)比较，立刻得知D=D*，这就是为什么把它叫做爱因斯坦扩散系数的原因.

2 电磁波纵波分量与光子静止质量

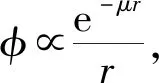
∇2φ=μ2φ

(6)

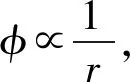
(7)

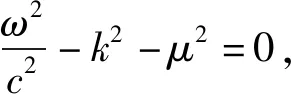
汤川理论还可以用来讨论类似问题. 有一种说法是，假如电磁波有纵波分量，则光子静止质量不为零. 我们知道在通常情况下，电磁波是横波，因此我们假设某个电磁波除了横波振幅，还有小的纵波振幅. 我们考察沿z方向传播的电磁波，电场横波沿x方向，还有一个很小的纵波振幅：

E=Exex+ξez

(8)

为了简单，磁场只有横波振幅：

B=Byey

(9)

它要满足真空中电磁场方程组：

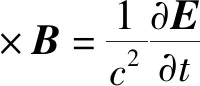
(10)

不失一般性，有

B=By(x,z-ut)；

Ex=Ex(x,z-ut)；

ξ=ξ(x,z-ut)

(11)

此时电磁波方程为

(12)

分离变量By=η(x)eik(z-ut)，其中k是波矢，u是此时波速. 将其代入式(12)，得

(13)

如果电磁波有静止质量，则其群速度一定小于真空中光速c，因此其相速度u>c，因为容易证明，此时uug=c2.式(13)容易解得η=B0ei(kxx+φ)，因此有

By=B0ei(kxx+φ)eik(z-ut)

(14)

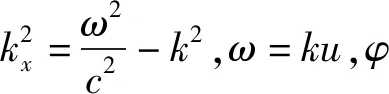
Ex=E0ei(kxx+φ)eik(z-ut)

(15)

ξ=-δei(kxx+φ)eik(z-ut)

(16)

(17)

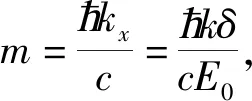
类似地，也可以把超导体内不能有磁场与光子静止质量不为零联系起来. 在超导体内的电磁现象非常丰富，但这里我们只是利用伦敦的唯象理论. 假设超导体内超导载流子带电荷量为es，质量为ms，数密度为N，则根据伦敦方程，超导电流js和矢势A之间有关系[4]：

(18)

这显然就破坏了规范对称性. 对于通常材料，电子与晶格的碰撞时间τ与 可见光波频率ω的乘积远远小于1，这可以理解为即使有变化的电流，超导电流远远大于通常的欧姆电流，所以我们在超导体内可以只考虑超导电流. 此时超导体内电磁方程为

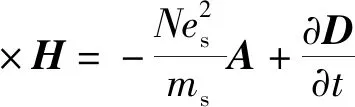
(19)

其中B≈μ0H,D≈ε0E. 对式(19)取旋度，然后化简就可以得到

(20)

3 状态空间最小体积

经典粒子的状态是由位置和速度确定的，我们也可以说对给定粒子位置和动量确定了状态. 位置和动量构成相空间，在相空间里的位置决定了粒子的状态. 但是对于微观粒子，由于不确定性导致在相空间里不能有确定的位置，不过可以有邻域范围. 处于某个小区域，就对应某个状态. 假设在相空间内，状态的最小体积为δ，根据不确定性原理，它大致与普朗克常量h3的量级接近. 而我们现在都知道δ=h3，怎么会刚好就是这个大小呢？这实际是数出来的[1].

考察一个装有微观自由粒子的边长为L的立方体盒子. 在界面上微观粒子波函数为零，相当于是驻波波节，因此有

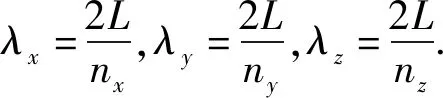
(21)

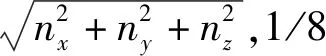
(22)

但从另一方面来看，若相空间内一个状态所占最小体积为δ，则小于能量E的状态数为

(23)

在实际教学中，我们只需在一维讨论就可以了. 一维盒子实际就是在无限深势阱内，容易得到粒子能量：

(24)

小于能量E的状态数为

(25)

另一方面，此时相空间是2维平面，如图1所示. 此时有

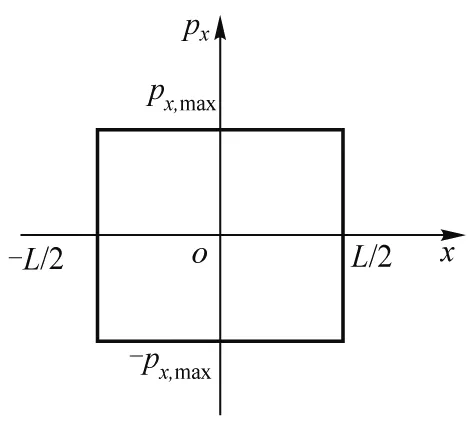
图1 在2维动量-位置相平面中对应一维盒子内粒子能量小于E的区域

与式(25)比较，得到δ=h.

也可以通过1维谐振子讨论. 对于一维谐振子，能量为

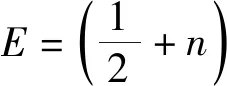
(26)

因n>>1，小于能量E的状态数为

(27)

另一方面，能量又是动能和势能之和：

(28)

对于给定能量，粒子限制在相空间内椭圆轨道上，小于该能量区域就在椭圆内，如图2所示. 此时，有

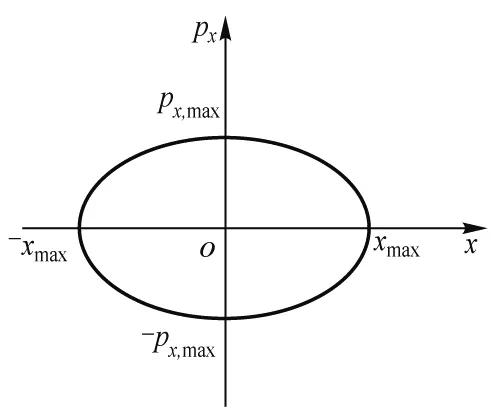
图2 一维谐振子在2维动量-位置相空间中能量小于E的区域

与式(27)比较，也得到δ=h.

4 结论

通过了解爱因斯坦早期对布朗运动的研究，了解到爱因斯坦扩散系数.汤川秀树有关介子质量的理论对于深入理解质量概念有非常重要的启发意义，我们由此理解了光子静止质量与库仑平方率、电磁波纵波分量以及规范对称性之间的联系.通过简单实例，我们了解到为什么在相空间中状态的最小体积恰好是h3(一维h).