高雷诺数下的圆柱绕流问题
——以蜡烛燃烧为例
罗 芸,王晓宁,赵旭阳,孟德忠,郝会颖
(1. 中国地质大学(北京) 地球物理与信息技术学院,北京 100083;2. 中国地质大学(北京) 数理学院,北京 100083;3.中国地质大学(北京)郑州研究院,河南 郑州 450006)
圆柱绕流是一个经典的流体力学问题,对该现象的基础理论研究对于解决具体的工程问题具有重要的指导意义. 例如,水流对桥梁、海上运输管线的作用,风力对高空电缆、高塔设备的作用等问题中,圆柱绕流问题都有着重要的工程应用背景. 因此,对圆柱绕流问题进行深入研究,不仅具有重要的理论意义,还具有明显的社会经济价值. 关于圆柱形障碍物后气流如何流动的问题,前人已经进行了深入的研究. Gabbai等总结了圆柱涡激振动的数值和实验模拟结论[1];Williamson等不仅总结了二维圆柱绕流涡动力学领域的研究,并且利用PIV技术对静止和振动圆柱绕流进行了实验研究,分析了尾涡的形成机理[2,3];Alam等在相同直径并列双圆柱的实验研究中得到了双柱在不同间距时升力及流动结构的变化趋势[4];姚熊亮等在相同直径串列双圆柱的模拟中研究了高雷诺数下双柱在不同间距比时的压力分布、阻力、升力及St数随雷诺数的变化趋势[5];Jester等对串、并列双圆柱的绕流都进行了模拟,研究了两圆柱在不同间距时的受力和尾涡状态,并分析了两个圆柱相对位置的改变对彼此流动的影响[6];Zhao等通过研究两个不同直径圆柱的绕流情况得到了小圆柱与主圆柱之间间隙比、小圆柱角度和小圆柱直径发生改变时的力系数、压强分布以及漩涡脱落结构的变化情况[7,8]. 何颖等人研究了不同雷诺数条件下旋转效应对旋涡脱落和尾部湍流产生的影响[9]. 以上的研究内容重点分析了不同复杂条件下气流绕流的形成机制问题,但关于绕流气流对障碍物后可燃物燃烧情况影响规律的研究却鲜有报道.
本文在前人研究结果的基础上进一步探究了绕流气流对障碍物后物质燃烧情况的影响规律. 针对灭火过程中有障碍物阻挡的问题,建立圆柱绕流模型,以蜡烛为火源探究了不同条件下圆柱绕流现象对障碍物后物质燃烧情况的影响. 针对此问题的研究结果可为有障碍物情况下的灭火场景提供理论支撑并运用于实际.
1 理论分析
针对绕流气流对障碍物后物质燃烧的分析可以采用如图1所示的物理模型,当气流、圆柱形瓶子、燃烧的蜡烛在同一轴线位置时,为什么在瓶子后燃烧的蜡烛会被瓶子前的气流吹灭,仿佛瓶子根本就不存在呢?这涉及到两个方面的问题,一是气流如何绕过瓶子,二是蜡烛如何被气流吹灭.
1.1 圆柱绕流
对于黏性流体,在直角坐标系下,其运动规律可用N-S方程来描述,而该连续性方程如式(1)所示,该动量方程如式(2)所示[10,11].
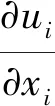
(1)
(2)
其中ui为速度分量,P为压力,ρ为流体的密度,ν为流体的动力黏度.
对于定常流的不可压缩的无黏流体,将N-S方程进行化简得伯努利方程为
(3)
其中P1、v1、h1分别为点D1处的压强、流速和高度,P2、v2、h2分别为点D2处的压强、流速和高度,ρ为流体密度,g为重力加速度.
根据伯努利方程可以推导出在同一条流线上流速大的地方压力小.当流体与它流过的物体表面之间存在表面摩擦时(也可以说是流体黏性),只要曲率不大,流体就会顺着该物体表面流动.根据牛顿第三定律,物体施与流体一个偏转的力,则流体也必定要施与物体一个反向偏转的力.这种力在轻质物体上体现得非常明显,称为康达效应,即流体(水流或气流)有偏离原本流动方向,改为随着凸出的物体表面流动的倾向[12],而流体绕过障碍物后的运动状况则需根据具体情况求解.
对于二维圆柱低速定常绕流现象,流型只与雷诺数有关,其具体的变化情况如表1所示.

表1 不同雷诺(Re)数范围内的单柱绕流尾流形态[13-15]
对于理想流体,其压强分布呈对称性,所以圆柱不受升力及阻力.而对于实际流体,存在黏性,则有边界层分离,形成圆柱的阻力,阻力大小与分离点有关.
根据流体的圆柱绕流模型,本文建立了圆形瓶子障碍下蜡烛熄灭模型,如图1所示.其中影响蜡烛熄灭的参数如下:① 蜡烛的发热量Q;② 环境风速Uw;③ 障碍物的特征长度 ;④ 蜡烛与障碍物之间的间距S.通过量纲分析可得到方程式(4):

图1 圆柱绕流的简化模型
(4)
其中ρ∞为空气密度,取1.21 kg/m3,Cp取1.005 J/(kg·K),T∞为环境温度,取300 K,g为重力加速度,取9.8 m/s2,d为蜡烛直径,H为出风口高度.
1.2 蜡烛熄灭原因

2 实验
2.1 实验装置设计
本文选择玻璃材质的圆柱体作为障碍物,选择蜡烛作为火源,分别设置蜡烛火源功率、气流流速、障碍物直径、蜡烛与障碍物之间间距为自变量,选择蜡烛火焰被风吹灭的时间作为因变量,进行进一步探究.
本文选定A、B、C三种蜡烛,蜡烛燃烧速率分别为0.001 84 g/s、0.00 175 g/s、0.00 178 g/s,测量能将蜡烛火焰吹灭的最小流速及其他因素对蜡烛火焰熄灭时间的影响,以得到更普适性的结论. 本文利用剪辑软件以更精确地确定蜡烛火源熄灭时间,利用风速仪测量流速. 所有实验均在干燥环境中进行,周围温度均为室温.
2.2 探究火焰熄灭时的气流最小流速
本文进行了实验研究,以验证导致蜡烛熄灭的主要原因,并对蜡烛火焰熄灭时的最小气流流速进行探究.
让蜡烛火焰熄灭的气流最小流速应为单位时间内气流吸热恰好等于蜡烛产热时的临界流速,对于不同种类的蜡烛,存在不同的临界流速. 而在到达蜡烛处的气流流速小于该临界流速时,实验结果无意义. 为探究该临界流速,我们选择A、B、C三种蜡烛,不断改变气源流速以改变到达蜡烛处的气流流速,利用风速仪测量到达蜡烛处气流流速.
通过多次测量发现,能让蜡烛A火焰熄灭的平均气流最小流速小于0.3 m/s,能让蜡烛B火焰熄灭的平均气流最小流速小于0.2 m/s,能让蜡烛C火焰熄灭的平均气流最小流速小于0.2 m/s. 由于风速仪精度的限制,该临界流速无法进一步确定. 但由于给出了临界流速的上界,因而对于后续的实验研究仍具有一定意义. 让蜡烛火焰熄灭的气流最小流速受到蜡烛燃烧速率的直接影响,同时,该气流最小流速还会因蜡烛燃烧时火焰周围固态蜡形状的改变而改变.
2.3 不同变量对火焰熄灭时间的影响
2.3.1 到达障碍物处气流流速对火焰熄灭时间的影响
在实验中,为探究到达障碍物处气流流速对蜡烛火焰熄灭时间的影响,提供到达障碍物处气流流速分别为2.0 m/s、2.5 m/s、3.0 m/s、3.5 m/s、4.0 m/s、4.5 m/s,固定蜡烛与障碍物之间距离为50 mm,选择障碍物直径分别为18 mm、25 mm、 60 mm、82 mm,以分别探究不同障碍物直径下到达障碍物处流速对火焰熄灭时间的影响. 通过图2可知,对于直径越大的障碍物,到达障碍物处流速改变对火焰熄灭时间影响越明显,且总体而言火焰熄灭时间与到达障碍物处流速成反比关系.

图2 障碍物不同直径时到达障碍物处流速对火焰熄灭时间的影响
2.3.2 障碍物直径对火焰熄灭时间的影响
障碍物直径的大小很大程度上影响了气流的方向及分布,因此本文进行了相关实验,以探究障碍物直径对火焰熄灭时间的影响.
在实验中,为探究障碍物直径对火焰熄灭时间的影响,提供障碍物直径分别为18 mm、25 mm、60 mm、82 mm, 固定蜡烛与障碍物之间距离为50 mm,选择流速分别为2.0 m/s、2.5 m/s、3.5 m/s、4.0 m/s、4.5 m/s, 以分别探究不同流速下障碍物直径对火焰熄灭时间的影响. 通过图3可知对于到达障碍物处流速越小的情况,障碍物直径改变对火焰熄灭时间影响越明显,且火焰熄灭时间与障碍物直径成正比关系. 但是当流速 ≥ 2.5 m/s,障碍物直径 ≥ 60 mm时,障碍物直径改变对火焰熄灭时间几乎无影响,这可能是因为在此条件下,绕过障碍物后的气流速度达到了熄灭蜡烛火焰的阈值.

图3 不同流速下障碍物直径对火焰熄灭时间的影响
2.3.3 障碍物与蜡烛之间距离对火焰熄灭时间的影响
障碍物与蜡烛之间的距离是影响蜡烛火焰熄灭的另外一个原因,本文进行了相关实验,以探究障碍物与蜡烛之间距离对火焰熄灭时间的影响.
在实验中,为探究蜡烛与障碍物之间距离对火焰熄灭时间的影响,提供蜡烛与障碍物之间距离为50 mm、100 mm、150 mm、200 mm,固定障碍物直径为60 mm, 选择流速分别为2.0 m/s、3.0 m/s、4.0 m/s、4.5 m/s,以分别探究不同流速下蜡烛与障碍物之间距离对蜡烛火焰熄灭时间的影响. 通过图4可知对于到达障碍物处流速越小的情况,蜡烛与障碍物之间距离改变对蜡烛熄灭时间影响越明显,且总体而言火焰熄灭时间和蜡烛与障碍物之间距离成正比关系.

图4 不同流速下蜡烛与障碍物之间距离对火焰熄灭时间的影响
2.3.4 蜡烛燃烧速率对火焰熄灭时间的影响
为了进一步研究蜡烛本身燃烧速率的影响,本文进行了相关实验,以探究蜡烛燃烧速率对火焰熄灭时间的影响.
蜡烛燃烧速率直接影响蜡烛燃烧单位时间内产生的热量,进而影响火焰熄灭时间. 在实验中,为探究蜡烛燃烧速率对火焰熄灭时间的影响,提供A、B、C 3种蜡烛,固定到达障碍物处流速为2 m/s, 障碍物直径为60 mm,蜡烛与障碍物之间距离为50 mm, 其火焰熄灭时间对应为0.80±0.04 s、0.65±0.04 s、0.72±0.05 s. 通过图5发现,蜡烛燃烧速率和火焰熄灭时间成正比关系.
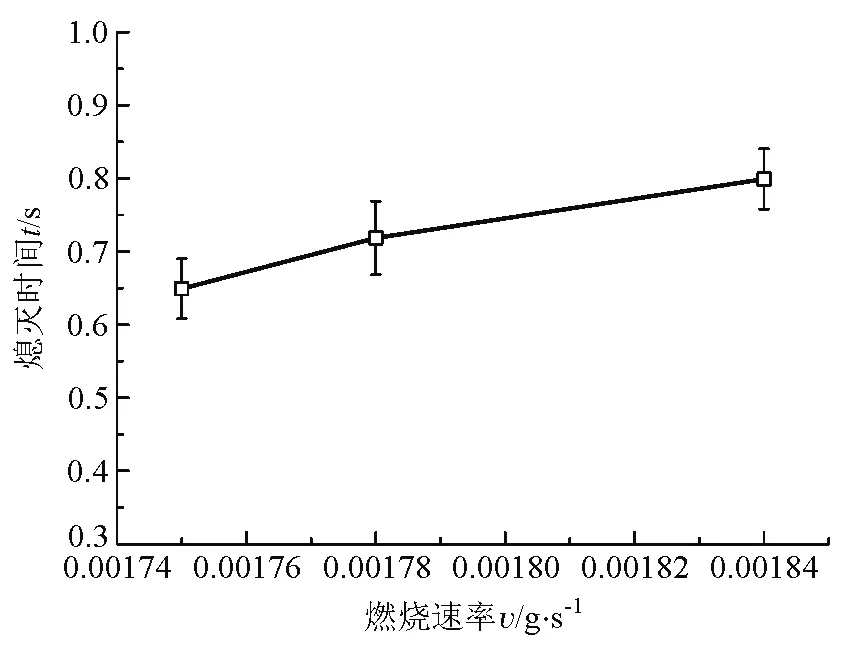
图5 蜡烛燃烧速率对火焰熄灭时间的影响
2.4 临界值探究
2.4.1 蜡烛火焰不会熄灭时的临界障碍物直径
探究让蜡烛火焰不熄灭的临界障碍物直径能更好研究不同流速下的圆柱绕流问题,为探究该临界值,提供到达障碍物处流速为1.2 m/s、1.5 m/s、2.0 m/s、2.5 m/s、3.0 m/s、3.5 m/s、4.0 m/s、4.5 m/s、5.0 m/s、5.5 m/s、6.0 m/s、6.5 m/s、7.0 m/s,固定蜡烛C到障碍物之间距离为200 mm,此时临界障碍物直径分别为325 mm、340 mm、400 mm、465 mm、450 mm、400 mm、415 mm、370 mm、343 mm、325 mm、317 mm、265 mm、215 mm. 通过图6分析可得临界障碍物直径先随流速增加而增加,后随流速增加而减少.
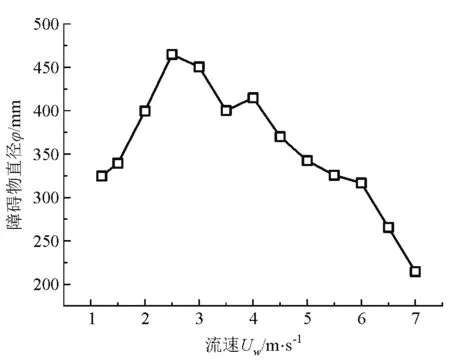
图6 不同流速下火焰不会熄灭时的障碍物临界直径
2.4.2 让蜡烛火焰不会熄灭的临界流速
为避免某些情况下障碍物后可燃物火焰不能被扑灭,需对火焰不会熄灭时的临界条件进行分析,以探究某些特定情况下蜡烛火焰不会熄灭时到达障碍物处的临界流速. 实验中,为探究该临界值,提供障碍物直径分别为150 mm、200 mm、250 mm、300 mm、350 mm、400 mm、450 mm、500 mm,提供障碍物与蜡烛之间距离分别为100 mm、200 mm、300 mm进行探究,得到的实验结果如表2所示

表2 不同情况下的临界流速
3 结论
为探究气流对圆柱形障碍物后可燃物燃烧情况的影响,本文选择蜡烛为火源进行了相关实验.通过研究发现,蜡烛熄灭时间的主要影响因素包括到达障碍物处流速、蜡烛与障碍物之间距离、障碍物直径、蜡烛种类. 对其进行进一步探究,可以得出:1) 火焰熄灭时间与到达障碍物处流速成反比关系;2) 火焰熄灭时间与障碍物直径成正比关系;3) 火焰熄灭时间与蜡烛和障碍物之间距离成正比关系;4) 火焰熄灭时间和蜡烛燃烧速率成正比关系.
由此可类比出气流对圆柱形障碍物后其他可燃物燃烧情况的影响的结论. 此外,文章对两种临界情况进行了探究,即探究蜡烛火焰不熄灭时的临界流速和临界障碍物尺寸,并发现了临界障碍物直径先随流速增加而增加,后随流速增加而减少;临界流速先随障碍物直径增加而增加,后随障碍物直径增加而减少的关系.
本文所探究的问题可在有障碍物时的灭火过程中得到实际应用,此外,也可以在流体力学课程中作为康达效应与圆柱绕流问题的简单实验演示,激发大学生对物理的研究兴趣.

