直线法修形摆线针轮副的回程误差

李玉龙，李天兴，李晋凡，张瑞瑶，周静远

(河南科技大学 机电工程学院，河南 洛阳 471003)

0 引言

在机器人精密减速器中，摆线轮修形的目的在于保证非工作区域合理的间隙，便于安装和润滑，保证工作区域齿廓与摆线轮理论齿廓尽可能地接近，保证良好的轮齿啮合特性[1-4]。随着摆线轮成形磨削技术的不断发展，摆线轮的修形方法也不再局限于传统的移距、等距等修形方式，修形齿廓形状也呈现多样化[5-8]。然而，多样化齿廓形状的传动精度的求解并没有形成统一的求解模型，对准确评价摆线轮修形齿廓的啮合性能产生了一定的影响。机器人精密减速器经常需要做往复运动，修形后的摆线轮由于啮合间隙以及回程误差的存在[9-12]，使整个系统的重复定位精度受到严重影响。因此，不同修形齿廓的摆线轮回程误差的获取和分析已成为该领域研究的重要内容。

目前，学者对机器人精密减速器摆线轮齿廓的修形、摆线针轮啮合特性和传动精度等方面已经进行了深入的研究。文献[13]综合考虑制造误差对摆线针轮啮合传动的不良影响，提出了一种新型的正等距与负移距组合的修形方式，增加了共同啮合齿数，提高了承载能力，缩小了回程误差。文献[14]对摆线轮传统修形方法所产生的回程误差做了详细研究，计算出回转角的变化范围。文献[15]研究了摆线轮单齿无侧隙失配修形，并推导出摆线轮修形后的齿廓方程。文献[16]通过建立摆线针轮齿廓修形的回程误差精度分析模型，可求解常见修形方法引起的几何回差误差，并推导出摆线轮齿廓修形回差误差的影响公式。文献[17]基于传统修形模式，通过建立齿面接触分析(tooth contact analysis,TCA)方程，提出一种适用于各种修形模式的啮合间隙计算方法。文献[18]在抛物线修形方法的基础上，综合考虑齿廓误差和传动误差影响，获得更加符合工程实际的摆线轮齿廓。

尽管国内外学者已经在摆线轮齿廓修形和回程误差分析方面取得了较大成果，但是传统的回程误差的获取相对复杂。随着摆线轮修形齿廓形状的多样化，需要建立一种通用的修形齿廓回程误差的求解模型，有助于形成统一的回程误差评价体系。因此，本文基于直线法修形齿廓，通过建立摆线针轮接触模型，求解回程误差，获取理论修形齿廓回程误差曲线，研究机器人精密减速器的回程误差性能，可为改善系统的重复定位精度提供新思路。

1 直线法修形齿廓及其方程

直线法修形是一种简单有效的齿廓设计方法，它综合考虑了压力角与修形量的影响关系，能够获得具有良好传力性能的齿廓形状。

1.1 直线法修形

直线法修形是使修形量ΔL与压力角α满足线性关系，建立修形量与压力角的函数关系[19]：

ΔL=kα+b1。

(1)

将已知参考点坐标(α0,ΔL0)、齿顶坐标(αtip,ΔLtip)代入式(1)，可求解出未知参数k、b1，即可得到从参考点到齿顶的修形量表达式，同理，将参考点和齿根坐标代入方程(1)，整理得出参考点到齿根的修形量表达式。

直线法修形量的分段函数表达式[19]：

(2)

其中：αroot为齿根处压力角；ΔLroot为齿根处修形量。

1.2 修形齿廓方程

将式(2)求得的修形量沿理论齿廓各个点的法线方向依次进行叠加，直线法修形原理如图1所示。

图1 直线法修形原理图

图1中，实线为摆线轮理论齿廓曲线，虚线为修形齿廓曲线，虚线与实线之间是法线。

修形后摆线轮齿廓方程为：

(3)

2 摆线针轮的啮合接触分析模型

根据摆线针轮副啮合传动关系建立坐标系，摆线轮啮合关系如图2所示。图2中，坐标系Sp(XpOpYp)与Sc(XcOcYc)固接到相对于固定坐标系Sf(XfOfYf)进行转动的针轮和摆线轮上，Op为针轮自转坐标系中心，Oc为摆线轮自转坐标系中心，K为啮合点，M为针齿圆心，P为节点，PM为公法线。针齿的齿廓方程为：

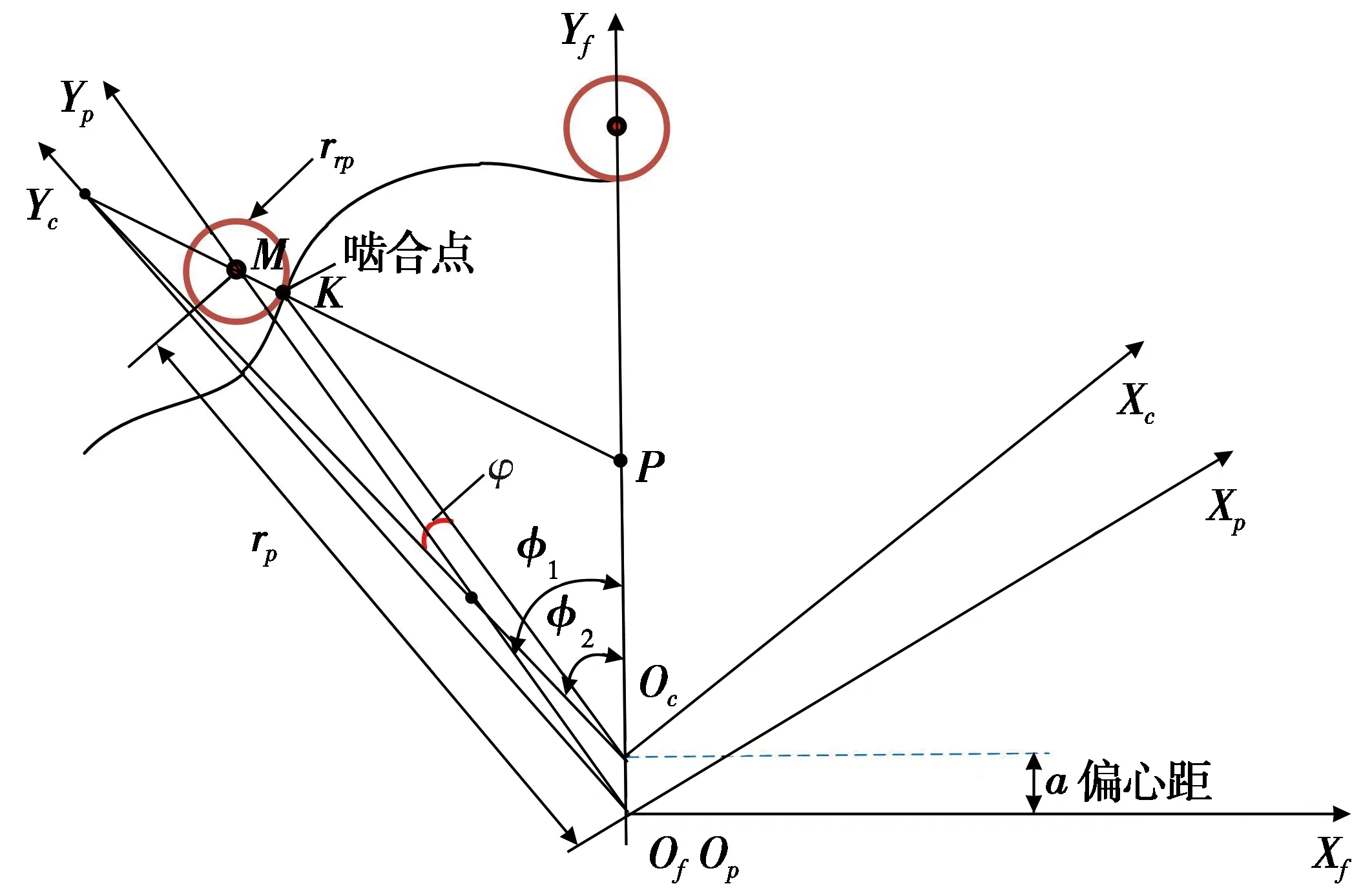
图2 摆线轮啮合关系

(4)

其中：p为针齿参量角。

在摆线针轮啮合传动过程中，在啮合接触位置，摆线轮与针齿的位置矢量和法线矢量应相等[20]，通过空间坐标转换，将摆线轮和针轮的位置矢量和法线矢量转化到固定坐标系Sf中，由此建立摆线针轮副的啮合接触分析数学模型：

(5)

其中：φ1为针轮转角；φ2为摆线轮转角；β为针齿参量角；Mfp和Mfc均为变换矩阵。

(6)

方程组(6)是非线性的，有3个方程和4个未知数[22]，给定φ，即可求解出对应的φ1、φ2和β值。

3 回程误差的获取

修形后的摆线轮与针轮之间会产生一定的间隙，当摆线轮往复运动时，需要克服齿侧间隙才能进入反向啮合传动。以11齿摆线轮为例，摆线针轮啮合的瞬时状态如图3所示。

由式(6)可以得到摆线轮啮合范围，以及摆线针轮啮合传动时摆线轮和针轮的转角。如图3所示，当前0号齿处于啮合状态，针轮反向转动，齿侧间隙最小的齿对会最先进入啮合，针轮的最小回转角即回程误差[21]。在获得摆线针轮接触分析结果的基础上，根据求解过程，可以得到回程误差。回程误差具体求解过程如图4所示。

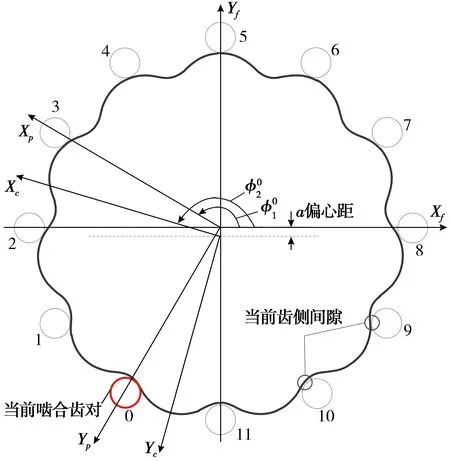
图3 摆线针轮啮合的瞬时状态

图4 回程误差具体求解过程

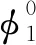
(Ⅴ)绘制回程误差曲线。以针轮转角作为横坐标，消除回程间隙所转过的角度为纵坐标。

4 验证分析

摆线针轮副基本参数：摆线轮齿数ZC=39，针轮齿数ZP=40，针轮分布圆半径rp=82 mm，针轮半径rrp=3.5 mm，偏心距a=1.5 mm。

直线法修形参数为：ΔL0=0.005、ΔLtip=0.02，对应的压力角大小为：α0=42°、αtip=90°。将以上数据代入式(1)，可求得k=3.125×10-4，b=-8.125×10-3，则直线法修形量方程为：

ΔL=3.125×10-4α-8.125×10-3。

(7)

通过式(7)，可求得任意压力角处的ΔL。

根据直线法修形原理，将修形量ΔL依次沿着法线方向垂直叠加，可得到摆线轮直线法修形齿廓。将式(7)代入式(3)，可以得到理论的摆线轮直线法修形齿廓。然后将式(4)和式(3)代入轮齿接触分析方程式(5)。

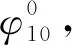
采用上述摆线针轮副基本参数，通过上述方法将得到每一啮合齿对的回程转角，就能够得出直线法修形后的回程误差曲线，如图5所示。

图5 回程误差曲线

由图5可知：直线法修形后的摆线齿廓最小回程误差值是0.604′。为了验证理论回程误差计算值的准确性，加工摆线轮样品，测量摆线轮加工后的回程误差。

采用摆线轮成形磨齿机加工摆线轮，如图6所示。在测量仪上完成摆线轮齿廓合理性检测，排除其他因素的影响。

(a) 摆线轮加工

最后，将加工的摆线轮样品在旋转矢量(rotary vector,RV)减速器综合性能测量仪上进行测量，获取样品摆线轮的回程误差曲线，如图7所示。

图7 样品摆线轮回程误差曲线

由图7可以看出：直线法修形后的摆线轮的实际回程误差平均值为0.830′。因为摆线轮在实际加工的过程中，存在安装、制造等误差因素，因此，实际加工的摆线轮回程误差会大于理论设计齿廓的回程误差。通过对比图5和图7的数据可知：理论计算的回程误差是实际减速器测量回程误差的73%，在实际生产中可以用来评价回程误差，进而评价修形质量，有一定的实际工程意义。

5 结论

本文通过结合直线法修形，以直线法修形齿廓为基础，建立并求解轮齿接触分析方程，获取回程误差曲线，验证对比实际测量摆线轮的回程误差曲线，理论计算的回程误差是实际减速器测量回程误差的73%，能够满足实际工程要求。因此，通过轮齿接触分析获取回程误差的方法是合理、可行的，能够高效计算出摆线针轮副的回程误差，可作为评定齿廓修形质量的方法。