基于区分对的混合型弱标记数据增量约简算法

金 莎， 郑颖春

(西安科技大学 理学院，陕西 西安 710600)

0 引言

粗糙集理论是由波兰学者Pawlak提出的[1]，属性约简[2]是其重点研究内容，用于降低原始数据集维数, 剔除数据集的冗余和不相关属性。目前，基于信息系统[3-9]和决策系统[10-16]中的属性约简算法研究较多。

已有的属性约简算法只能解决有标记数据或无标记数据的约简问题，现实中因数据采集需要消耗大量成本或受技术限制，导致得到的数据大多是缺失、无标记的。文献[17]定义不完备弱标记数据的半监督差别矩阵，利用基于协同学习的思想将无标记的数据中信度较大的数据转换为有标记数据。文献[18]提出了一种半监督特征选择算法，该算法通过组合半监督散点，有效利用大量未标记的视频数据中的信息来区分目标类别。文献[19]针对弱标记的符号型数据，利用半监督学习框架，构造相对应的启发式半监督属性约简算法，然而该算法是非增量的，运行效率较低。文献[20]采用邻域粗糙集对部分标记数据进行属性约简，结合两种不同的度量方法得到综合重要性并设计启发式算法进行约简计算。文献[21]在粒计算的背景下提出不完备弱标记决策系统中的区分对定义，基于半监督学习给出决策系统中样本增加或减少的增量属性约简算法，然而并没有给出样本变化时的增量机制。

上述算法在处理动态变化的弱标记数据属性约简问题时，需要不断重复大量计算，没有相应的增量机制，计算复杂度高，分类性能低，且大多只能处理符号型数据。故针对混合不完备、且数据存在缺失的动态变化数据集，本文给出区分关系的更新定理，建立属性动态变化的增量机制,并提出相应的增量属性约简算法。最后，通过实验分析了本文增量属性约简算法与文献[19]、文献[20]中属性约简算法的计算效率和分类性能。

1 预备知识

文献[21]中指出，弱标记数据是既含有有标记的数据也包含无标记数据的集合。若混合型决策系统的决策属性值d存在缺失(即类别无标注)，则称这是一个混合型弱标记决策系统。

定义1 给定混合型弱标记决策系统TS=〈U=L∪N,C∪D,V,f〉， 其中，U是包含所有样本的非空有限集合，L是包含所有有标记样本的集合，N是包含所有无标记样本的集合，这里C=Cd∪Cr，Cd为离散型属性集，Cr为连续型属性集，D为决策属性集，对于∀a∈C，定义属性a的区分关系DISC(a,U2)为：

DISC(a,L2)={(xi,xj)|(a∈Cd,f(a,xi)≠f(a,xj))∨(a∈Cr,f(a,xi)-f(a,xj)|<δ)∧

(1)

DISC(a,N2)={(xi,xj):(a∈Cd,f(a,xi)≠f(a,xj))∨(a∈Cr,f(a,xi)-f(a,xj)|<δ)∧

f(a,xi)≠*∧f(a,xj)≠*,xi,xj∈N}；

(2)

DISC(a,U2)=DISC(a,L2)∪DISC(a,N2)，

(3)

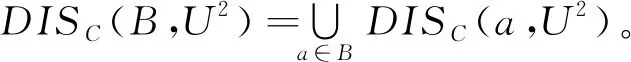
性质1 对于混合型弱标记决策系统TS=〈U,Cd∪Cr∪D〉，设属性集B⊆C，则属性集的区分关系一定满足：

DISC(B,U2)⊆DISC(C,U2)。

(4)

证明根据区分关系定义1可知，对于∀B⊆C，总是存在a∈C-B，DISC(a,L2)≠φ或DISC(a,N2)≠φ，所以有DISC(a,U2)=DISC(a,L2)∪DISC(a,N2)≠φ，满足|DISC(a,U2)|≥0， 因此DISC(B,U2)⊆DISC(C,U2)成立。性质1证毕。

定义2[21]给定混合型弱标记决策系统TS=〈U,Cd∪Cr∪D〉，对∀B⊆C，若B的区分关系满足以下两个条件，则称B为混合型弱标记决策系统的约简，记为redC：

(Ⅰ)DISC(C，U2)=DISC(B,U2)；

(Ⅱ)对∀a∈B，有DISC(B，U2)≠DISC(B-{a}，U2)。

2 混合型弱标记数据的非增量约简算法

根据区分关系定义，DISC(C,U2)表示属性集C所区分的论域U×U中所有样本对的集合，根据定义2，若DISC(C,U2)=DISC(B,U2)成立，B就是属性约简集，由性质1得DISC(B,U2)⊆DISC(C,U2)总是成立的，因此计算属性约简时，为减少要识别的样本对，可以将原本要区分的样本对U×U改为DISC(C,U2)，若属性集B能辨别属性集C所区分的所有样本对，它就是这个决策系统的属性约简。基于上述思想，本文构造了一种面对混合型弱标记不完备决策系统的属性相对区分度计算公式。它能与反向删除思想结合，不断去掉当前已能区分的区分对，逐步减少所要识别的区分对数量。

定义3 给定混合型弱标记决策系统TS=〈U,Cd∪Cr∪D〉，对∀a∈C，定义属性相对区分度为：

(5)

表示属性a相对于属性集C能区分的样本对个数所占比例。

性质2 对于混合型弱标记决策系统TS=〈U,Cd∪Cr∪D〉，若属性集B⊆C，则有DISC(C-B,U2)≠DISC(C,U2)-DISC(B,U2)。

证明假设属性集B是属性集C的约简，且B是包含于C的，根据定义2，它们的区分关系满足DISC(C,U2)=DISC(B,U2)，则DISC(C,U2)-DISC(B,U2)=0。对a∈C-B，一定存在a使得DISC(a,U2)≠0成立，得DISC(C-B,U2)≠0，所以DISC(C-B,U2)≠DISC(C,U2)-DISC(B,U2)。性质2证毕。

由定义3和性质2可得B⊆C，a∈C-B，属性a相对区分度为：

定义4 给定混合型弱标记决策系统TS=〈U,Cd∪Cr∪D〉，对∀B⊆C，∀b∈B，定义SIGI(b,B,C)=|DISC(B,U2)-DISC(B-b,U2)|为属性b相对属性集B的重要度，称为相对重要度。

基于以上混合型弱标记决策系统的区分关系和区分度定义，给出相应的属性约简算法。

算法1 混合型弱标记决策系统的非增量属性约简算法。

输入：混合型弱标记决策系统TS=〈U,Cd∪Cr∪D〉。

输出：属性约简集合B。

步骤1 根据定义，计算属性集a的区分关系DISC(a,U2)，令pair0=DISC(C,U2)。

步骤2 将|DISC(a,U2)|的值最大的属性加入约简集B，令pairj=DISC(B,U2)。

步骤3 计算pairj+1=pair0-pairj，其中j=1,2,…,n，当pairj+1=0，转到步骤5；否则，转到步骤4。

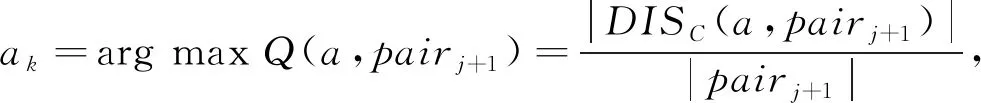
步骤5DISC(B,U2)=DISC(C,U2)，对属性约简集合B进行逆向剔除，对任意b∈B，计算属性b相对B内部重要度，若存在SIGI(b,B,pair0)=0，则B=B-b。

步骤6 输出属性约简集B。

3 混合型弱标记数据的增量约简算法

数据库总是呈现动态变化趋势，非增量算法1在解决属性动态变化的数据时，需重复计算所有属性的区分关系，时间复杂度高，甚至无法实现。接下来，给出属性动态增加时区分关系的增量式更新原理。提出混合型弱标记决策系统属性增加的增量属性约简算法。

3.1 属性增加时区分关系的增量式学习

定理1 给定混合型弱标记决策系统TS=〈U,Cd∪Cr∪D〉，增加属性p，若有标记的决策子系统的不一致容差类数量发生变化，或无标记的信息子系统的容差类数量发生变化，则新加入的属性p对于混合型弱标记决策系统的属性约简更新是有必要的，否则是不必要的。

证明在文献[11]中证明了有标记的决策子系统中不一致容差类的数量发生改变，则p是必要的。

无标记子系统中，若∃xi,xj∈N,xj∈TC(xi)，当属性p增加后xj∉TC∪p(xi)，则有:

⟹DISC(C∪p,N2)=DISC(C,N2)∪{(xi,xj)|xj∈TC(xi)∧xj∉TC∪p(xi)}，∴DISC(C∪p,N2)≠DISC(C,N2)，⟹DISC(C,U2)≠DISC(C∪p,U2)，⟹DISC(redC,U2)≠DISC(C∪p,U2)。

故redC不是〈U,C∪p∪D〉的属性约简，即属性p能区分原来条件属性C不能区分的样本对，p是必要的。定理1证毕。

定理2 给定混合型弱标记决策系统TS=〈U,Cd∪Cr∪D〉，若新加入属性p是必要的，则属性区分关系可用下式更新：

DISC∪p(a,L2)=DISC(a,L2)∪{(xi,xj):f(a,xi)≠f(a,xj)∧f(a,xi)≠*∧f(a,xj)≠

(6)

DISC∪p(a,N2)=DISC(a,N2)；

(7)

DISC∪p(a,U2)=DISC∪p(a,L2)∪DISC∪p(a,N2)，

(8)

其中：ω(p)={x∈L:|d(TC(x))|>1∧|d(TC∪p(x))|=1}，其中|d(TC(x))|表示x在条件属性集C下容差类的决策值基数，若|d(TC(x))|的值等于1则表示一致容差类，|d(TC(x))|的值大于1则表示不一致容差类。

证明式(5)的证明，根据区分关系的定义，有标记子系统中加入属性p后，属性a的区分关系为

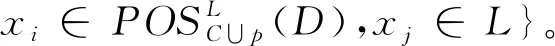
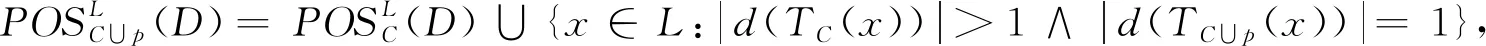
{(xi,xj):f(a,xi)≠f(a,xj)∧f(a,xi)≠*∧f(a,xj)≠*∧d(xi)≠d(xj),xi∈

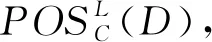
*∧d(xi)≠d(xj),xi∈ω(p)，xj∈|d([x]C∪p)|>1}∪{(xi,xj):f(a,xi)≠

f(a,xj)∧f(a,xi)≠*∧f(a,xj)≠*∧d(xi)≠d(xj),xi,xj∈ω(p)}。

第一部分子集就是属性a在加入属性p前的区分关系，再并上原本不一致的样本在加入属性p后变成一致样本的集合与负域中元素的区分对。

DISC(a,L2)∪{(xi,xj):f(a,xi)≠f(a,xj)∧f(a,xi)≠*∧f(a,xj)≠

定理2证毕。同理，可证式(6)成立。

定理3 给定混合型弱标记决策系统TS=〈U,Cd∪Cr∪D〉，已知其约简集为redC，当增加必要属性p，则需更新区分关系DISC(C,U2)，记新增加的样本对集为Δpairp，若Δpairp⊆DISC∪p(redC∪p,U2)，则redC∪p就是混合型弱标记决策系统TS′=〈U,C∪p∪D〉的属性约简集，否则需要利用属性相对区分度定义更新属性约简集。

3.2 增量属性约简算法

基于以上增量学习定理，结合反向删除法，构造混合型弱标记决策系统中基于属性相对区分度的启发式增量属性约简算法。

算法2 属性增加的混合型弱标记决策系统基于区分对的增量属性约简算法。

输入：混合型弱标记决策系统TS=〈U,Cd∪Cr∪D〉，区分关系DISC(a,U2)，令样本对集pair0=DISC(C,U2)，属性约简集redC；新增属性集合C′。

输出：混合型弱标记决策系统TS′=〈U,C∪C′∪D〉的属性约简集。

步骤1 增加属性集C′,筛选出必要属性集C″，若C″=φ，则转到步骤5；否则转到步骤2。

步骤2C″≠φ，重复以下步骤：

步骤2.1 若∃p∈C″，满足ω(p)={x∈L:|d(TC(x))|>1∧|d(TC∪p(x))|=1}≠φ，更新DISC∪C′(a,(L∪L″)2)；否则转到步骤2.2。

步骤2.2 若∃p∈C″，满足φ(p)={x∈N:|TC(x)|>1∧|TC∪p(x)|=1}≠φ，更新DISC∪C′(a,(N∪N″)2)，直到遍历C″中所有属性，转到步骤3。

步骤3 若Δpair0⊆DISC∪C′(redC∪C″,(U∪U′)2)(其中Δpair0=DISC∪C′(C∪C′,(U∪U′)2)-DISC∪C′(C,U2))，则约简为redC∪C′=redC∪C″，转到步骤6；否则转到步骤4。

步骤4 计算redC∪C′的区分关系，令pairj=DISC∪C′(redC∪C′,U∪U′)；设pairj+1=pair0∪Δpair0-pairj，其中j=0,1,…,n。若pairj+1=0则转到步骤6；否则转到步骤5。

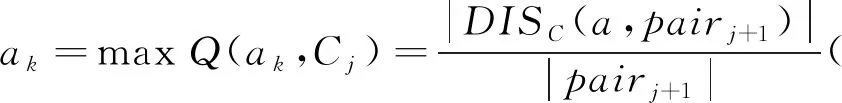
步骤6 对∀b∈redC∪C′，计算属性相对重要度，若存在bk使得SIGIDISC∪C′(bk,redC∪C′，pair2)=0 (其中pair=pair0∪Δpair0)，则属性约简为redC∪C′=redC∪C′-bk；转到步骤7，否则转到步骤5。

步骤7 输出属性约简redC∪C′。

4 算法实例分析

为进一步验证本文算法的有效性，在美国加州大学欧文分校提出的数据库(University of California Irvine，UCI)中选取了6个混合型数据集，如表1所示。实验的运行环境为：CPU Intel(R)Core(TM)i5-10500(3.20 Hz),内存8.0 GB，操作系统为Windows 10，所运用的软件平台为MATLAB2020a。

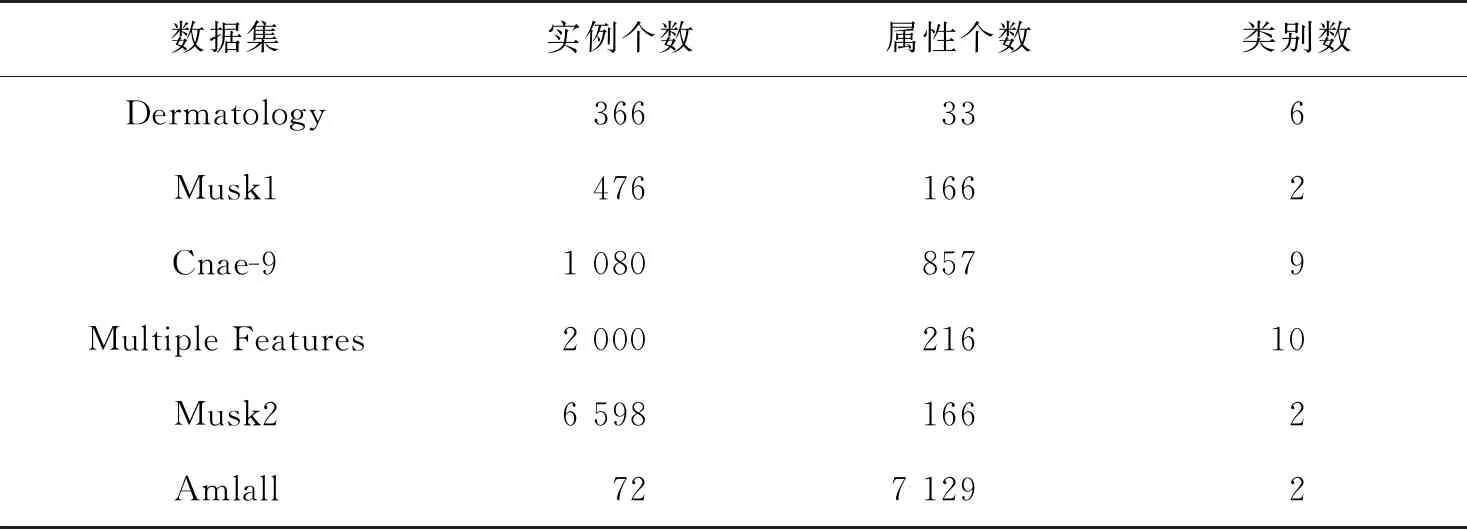
表1 实验数据集

4.1 数据说明及实验设计

为模拟现实中数据标记缺失的情形，将6个数据集的标记进行随机缺失处理，通过文献[21]可知，随机标记缺失比例为50%的弱标记数据环境中算法分类性能更好。本部分将讨论增量算法2的属性约简运行效率和分类性能。以50%条件属性作为基础数据，剩余数据作为增量数据集，按照增量数据集大小的10%为梯度递增时，分别对弱标记的数据采用本文非增量算法1、增量算法2、弱标记数据的半监督属性约简算法[19](semi-supervised attribute reduction algorithm for weakly labeled data, Semi-D)和综合重要性属性约简(compute IMP-reduction,CIMR)算法[20]进行属性约简，并对4种算法进行简单的比较分析。

4.2 属性约简效率比较

图1为本文非增量算法1、增量算法2、CIMR算法和Semi-D算法分别在6个数据集中属性增加时的属性约简计算时间比较。由于本文模拟了数据集中按增量数据的10%依次动态增加，因此图l中每幅图的横坐标为属性与样本的动态增加比例，刻度值为10%至100%，纵坐标表示每次增加动态数据时属性约简所消耗的计算时间。

由图1可知：随着混合型弱标记决策系统动态数据集的逐渐增加，本文算法1计算时间增长的速率较快，而增量算法2的增长速率较为缓慢，且CIMR算法和Semi-D算法的属性约简计算时间均大幅度高于增量算法2的计算用时。由图1a～图1c可知：由于本文算法2引入相对区分度作为属性重要度的度量标准，在每次迭代中不断地减少搜索空间，在处理数据规模较小的数据集和本文非增量算法1时，计算效率相近；在小数据集中，如Musk1数据集上本文算法2最终运行时间为187.428 s，而CIMR算法和Semi-D算法运行时间分别为650.365 s和972.315 s，相比CIMR算法节约71.18%，相比Semi-D算法能节约80.72%的时间。随着数据规模的增大，在图1d～图1f中，算法1在动态数据中更新属性约简结果需要进行大量的重复计算，采用增量算法2，利用已有的增量机制对属性约简集进行增量式更新，能够减少重复的计算，在Amlall数据集中，当数据集增加100%时，增量算法2的运行时间为1 171.456 s，非增量算法1的运行时间为6 351.258 s，CIMR算法和Semi-D算法的运行时间分别为10 129.458 s和11 078.74 s，相比非增量算法1的计算效率提高了81.5%，相比CIMR算法和Semi-D算法的计算效率分别提高了88.3%和89.42%。

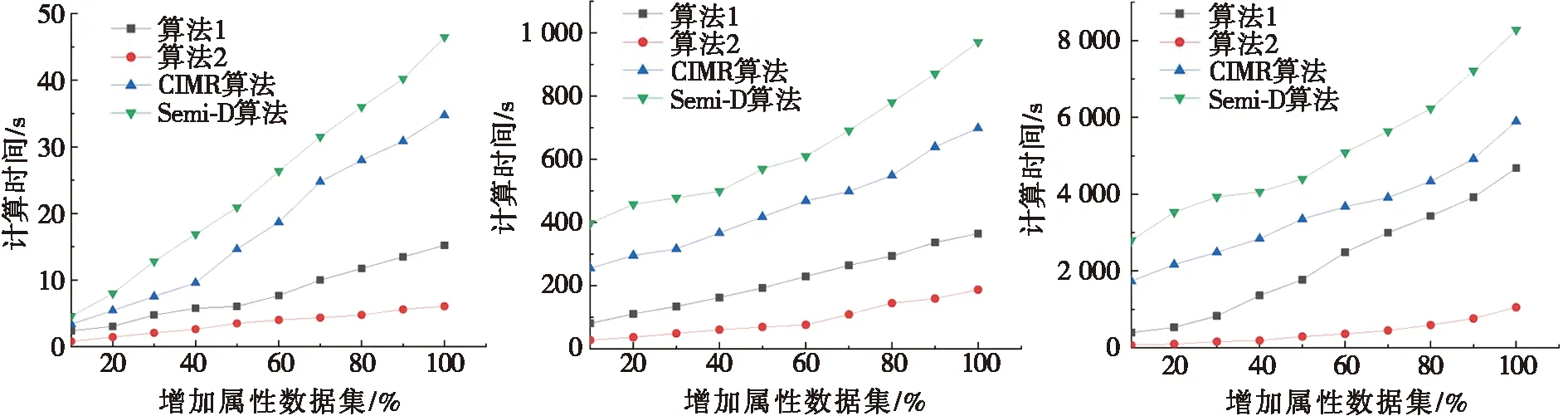
(a) Dermatology (b) Musk1 (c) Cnae-9

4.3 属性约简结果及分类性能比较

为了对非增量式与增量式属性约简的结果进行比较分析，在实验的过程中选取了当增加的数据集为100%时的属性约简结果输出来。非增量算法1和增量算法2的属性约简结果对比见表2，属性Ci简写为i。表2是数据随机缺失50%后，弱标记数据集的属性约简结果在支持向量机(support vector machines,SVM)和分类决策树(decision trees,C4.5)两种分类器下的分类精度。

由表2可知：在不同分类器中同一属性约简结果的分类精度有一定差异，但仅利用有标记的数据获取的属性约简结果会丢失部分有效的分类信息，故分类精度显著偏低，分类器较难准确学习到其内在规则或模式。因此，仅利用有标记的数据获取属性约简结果的分类性能显著偏弱。而利用本文弱标记属性约简算法1和算法2处理6个数据集标记缺失50%的弱标记数据，能够获取一个分类性能相对较优的属性约简结果。在实验过程中发现，在不同分类器中属性约简结果的分类性能也存在一定差异，本文算法2在规模较小的数据集上对比非增量算法1，由于对小数据集的标记进行随机缺失，对分类效果产生了一定影响，导致分类性能效果偏弱，但是相比仅用有标记数据处理数据的分类精度高，例如在Dermatology、Musk1和Cnae-9数据集中SVM分类器下，算法1的分类精度均值是80.68，算法2的分类精度均值是80.09，仅用有标记数据约简结果得到的分类精度均值是61.14。但随着数据规模的增大，增量算法2的性能表现趋于稳定，例如在Dermatology、Musk1和Cnae-9数据集中SVM分类器下，算法1的分类精度均值是91.18，算法2的分类精度均值是91.11，仅用有标记数据约简结果得到的分类精度均值是81.23。在 C4.5分类器下，3种算法的分类精度情况类似于SVM分类器，存在0.8以内的偏差。

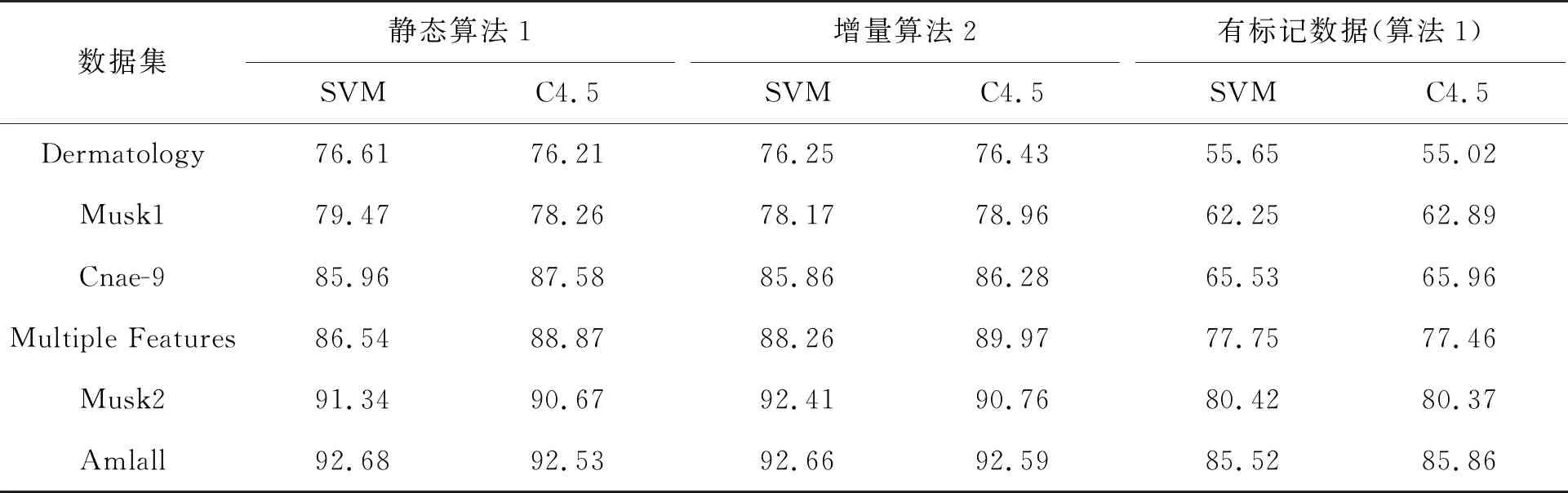
表2 属性约简分类精度比较 %

综上可得，本文提出的增量算法2能够有效节约大量计算时间，获取分类性能较优的属性约简结果，同时能够有效利用无标记的数据，增强属性约简结果的分类性能，显著提升了算法的鲁棒性。为大规模复杂数据的属性约简问题，提供了一个可行的增量式属性约简方法。

5 结束语

已有的粗糙集属性约简算法往往只能应用于信息系统或单一的决策系统，导致约简分类性能较低。本文提出的混合型弱标记决策系统中增量属性约简算法，能充分利用无标记与有标记数据得到精度较高的约简结果。给出了明确的增量机制，在处理实际应用中大规模复杂数据集时，相对传统非增量算法的约简效率更高。