基于M-FIPM的无网格DOA估计算法

陈 涛, 史 林, 申梦雨

(哈尔滨工程大学信息与通信工程学院, 黑龙江 哈尔滨 150001)

0 引 言

波达方向(direction of arrival, DOA)估计是阵列信号处理的一个重要分支,在雷达以及通信等领域有着广泛的应用[1-2]。传统的子空间类DOA估计算法,无法直接处理相关信源,并且对信噪比以及快拍数的鲁棒性较差[3-4]。而由于压缩感知理论的完善与快速发展,以l1-svd算法[5]为代表的稀疏类DOA估计算法,近年来逐渐受到国内外众多学者的广泛关注与研究[6-8]。

稀疏类DOA估计算法依据空间角度域的离散化处理,将入射信源DOA参数的估计问题转变为一个稀疏信号重构问题,并利用凸优化等数学手段获得最终的参数估计结果,在低信噪比以及少快拍的情况下依然可以保持良好的估计性能,并且能够直接处理相干信源,相比于子空间类算法具有显著的优势。但是,稀疏类DOA估计算法内在的网格失配问题会引起不可忽视的算法模型误差,严重影响稀疏DOA估计算法的性能[9-10]。

离网稀疏贝叶斯学习(off-grid sparse Bayestan learning, OGSBL)算法[11-14]以及网格细化[8]技术,分别利用网格点处一阶泰勒级数展开与局部细密网格,来解决网格失配问题。虽然上述两类算法能够在一定程度上提高网格失配情况下稀疏类DOA估计算法的性能,但依然没有摆脱空间角度域离散化处理,不能从根本上解决网格失配问题。

直到原子范数概念[15-17]的提出,才为彻底解决网格失配问题提供了一条行之有效的道路,进而形成了一类基于原子范数最小化[18-21](atomic norm minimization, ANM)的无网格DOA估计算法,简记为ANM-DOA算法。

ANM-DOA算法首先在连续的角度空间上建立以导向矢量为原子的无限维原子集合,然后以天线阵列接收单快拍数据向量的原子范数来表征该向量的稀疏性,最后建立一个以原子范数与拟合误差的加权和为目标函数的凸优化问题[22-24]。依据原子范数与半正定规划(semi-definite programming, SDP)问题的等价性,ANM-DOA算法成功地将入射信源DOA参数的估计问题转化为一个SDP问题,并最终利用Toeplitz矩阵的Vandermonde分解,获得DOA参数的估计结果。

由此看见,ANM-DOA算法不再依赖于空间角度域的离散化处理,进而从根本上解决了网格失配问题。同时,ANM-DOA算法的核心便在于SDP问题的求解,这同时也是该算法中复杂度最高的运算。现有的ANM-DOA算法利用内点法[25](interior point method, IPM)或交替方向乘子算法[26-27](alternating direction multiplier method, ADMM)来求解SDP问题。内点法每次迭代过程的复杂度为O(M6),而ADMM算法每次迭代过程的复杂度仅为O(M3)。不过,ADMM算法的收敛速度慢,达到收敛时所需要的迭代次数要远高于内点法。

所以,基于上述两种算法的SDP问题求解过程均不理想,如何能够快速求解SDP问题已然成为当前ANM-DOA算法领域的一种重要研究方向。而快速内点法[28](fast IPM, FIPM)的提出,将SDP问题的维度由O(M2)将低为O(M),从而每次迭代过程的复杂度变为O(M3)。这样,FIPM不仅保留了内点法收敛速度快的特点,同时又综合了ADMM算法每次迭代过程算法复杂度低的优势,所以在相同的SDP问题维度,即阵元数目相同时,FIPM算法的求解速度最快。但是,目前的FIPM仅仅适用于单快拍情况下ANM-DOA算法中的SDP问题。

针对FIPM无法处理多快拍数据的问题,本文提出了一种基于多快拍FIPM(multiple snapshots FIPM, M-FIPM)的ANM-DOA算法。该算法首先对天线阵列接收多快拍数据的协方差矩阵进行特征值分解,然后依据以特征值为系数的特征向量加权和建立满足FIPM算法模型的SDP问题,最终再利用FIPM算法与Toeplitz矩阵的Vandermonde分解[29-30]获得DOA参数的估计结果。

在估计精度方面,所提出的基于M-FIPM的ANM-DOA算法,不受网格失配问题的制约,所以与稀疏类DOA估计算法相比,估计精度有显著的提升。另外,在运行时间方面,基于M-FIPM的ANM-DOA算法每次迭代过程的复杂度为O(M3),达到收敛时所需的迭代次数也要远小于ADMM算法,所以具有较高的运算效率。

1 信号模型

考虑空间中K个远场窄带信号,入射到具有M阵元的均匀线阵上,阵元间距为λ/2。信源角度θk∈[-π/2,π/2],k=1,2,…,K。

阵列天线接收信号的多快拍数据为

Y=AS+N

(1)

式中：S=[s1,s2,…,sK]T∈CK×T,为信号矩阵,T为快拍数,sk=[sk(1),sk(2),…,sk(T)]表示第k个信号。N=[n1,n2,…nm,nm+1,…,nM]T∈CM×T为加性零均值高斯白噪声矩阵,nm∈CT为第m个阵元的噪声数据,m=1,2,…,M。

A=[a(θ1),a(θ2),…,a(θk),a(θk+1),…,a(θK)]∈CM×K为信号的导向矢量矩阵,具体地,a(θk)∈CM可以被表示为

a(θk)=[1,e-jπsin θk,…,e-jπ(M-1)sin θk]T

(2)

式中： j为虚数单位。

因此,当入射信源之间独立时,天线阵列接收多快拍数据的协方差矩阵RY∈CM×M为

RY=E[YYH]=AE[SSH]AH+σ2IM=ARSAH+σ2IM

(3)

式中：E表示求数学期望;RS∈CK×K表示信号协方差矩阵;σ2为噪声方差;IM是M维的单位矩阵。

在实际应用当中,由于快拍数T有限,所以实际协方差的计算常采用下面的公式进行计算:

(4)

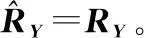
2 多快拍数据的降维处理

首先,对式(3)中的阵列协方差矩阵进行特征值分解,可以得到:

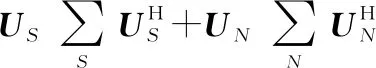
(5)

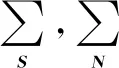
在式(5)左右两端分别右乘US,得到:

(6)

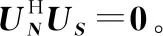
对式(3)两端也同时右乘US,则有:

RYUS=ARSAHUS+σ2IMUS

(7)

综合式(6)和式(7)可以得到:

(8)

将式(8)的左边记为

(9)

式中：amk表示导向矢量a(θk)中的第k个元素;vki是矩阵V=RSAHUS中第k行第i列的数据。

类似地,式(8)右边也可以被表示为

(10)

式中：eMi为矩阵US中第M行第i列的元素,即ei=[e1i,e2i,…,eMi]T为协方差矩阵RY的特征值λi所对应的特征向量,i=1,2,…,K。

由式(9)和式(10)可以得到:

(11)

然后,令:

(12)

因此,有如下的等式关系成立:

(13)

所以有以下的等式成立:

(14)

式中：q∈LM即为新构建的观测向量。

从式(14)可以得出,新的观测向量与单快拍下基于ANM的DOA估计算法模型具有相同的形式,所以可以利用FIPM算法进行最优解的求解。

3 M-FIPM算法

将式(14)中的pk记为pk=|pk|ejφk,其中φk表示pk的相位,|pk|表示pk的模,则新观测向量q的具体形式可以被表示为

(15)

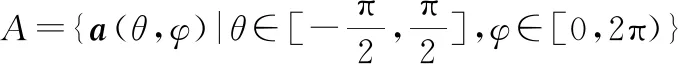
(16)

形如式(16)所示的原子范数可以等价为如下SDP问题的最优解:

(17)

传统的求解SDP问题的算法那包括IPM与ADMM。其中,IPM中每次迭代过程的复杂度为O(M6),而ADMM每次迭代过程的复杂度仅为O(M3)。不过,与IPM相比,ADMM的收敛速度慢,达到收敛时所需要的迭代次数要远大于IPM。因此,IPM和ADMM的运算量均不理想。而本文利用FIPM求解式(17)中的SDP问题,提出基于多快拍快速内点法的ANM-DOA估计算法,记为M-FIPM。该算法每次迭代过程的复杂度也为O(M3),而收敛速度也与IPM算法相当,是目前运算效率最高的SDP问题求解算法。

形如式(17)所示的半定规划过程又可以表示为如下的形式:

(18)

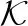
(19)

(20)

根据上述对偶锥的定义,可以将式(18)的Lagrangian函数写为如下形式:

(21)

则可以得到式(18)的增广KKT条件为

(22)

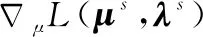
lg(t-qHToep-1(u)q)

(23)

式中：Toep-1(u)为Toep(u)的逆。

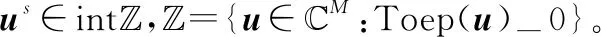
M-FIPM算法的具体流程如下所示。

初始值阈值ε≥0,迭代次数i=1,初始的障碍因子s1>0,初始参数u0∈intZ。

输出入射信号的角度值θk;

步骤 1利用式(5)对接收信号协方差矩阵进行特征值分解,得到特征值和对应的特征向量;

步骤 2利用式(14)构建新的观测向量q;

步骤 3利用M-FIPM算法求解式(17)对应的SDP问题的最优解u*;

步骤 4根据u*构建Toeplitz矩阵,并对该矩阵进行Vandermonde分解,得到入射信号角度参数θk的估计结果。

4 算法仿真实验

本节对算法的有效性进行仿真验。采用的阵列是8阵元的均匀线阵,对空间中4个独立的远场窄带信源进行DOA估计。

在M-FIPM算法以及ANM算法中,正则化参数选取τ=0.5,对偶偏差设置为10-7,缩放因子β=10。而对于l1-svd算法,正则化参数取值不变,空间角度离散网格的间距为0.5°。同样,MUSIC算法的空间谱峰搜索步长也为0.5°。

首先,对多重信号分类(multiple signal classification, MUSIC),l1-svd,ANM以及M-FIPM 4种算法在不同信噪比(signal to noise ratio, SNR)以及不同快拍数下的估计精度进行仿真对比。

通过均方根误差(root mean square error, RMSE)来衡量DOA估计算法的估计精度,其计算方法如下:

(24)

式中：L∈R+是Monte-Carlo的实验次数;θl是第l次实验中信源DOA参数的估计结果;θ为真实的入射角度。

实验 1令SNR在0～20 dB之间均匀变化,步长为5 dB,快拍数固定为200。信源的角度在[-60°,60°]之间随机选取,最小角度间隔为10°。在每个SNR下做200次Monte-Carlo实验,上述4种算法的RMSE统计结果如图1所示。

实验 2令快拍数分别取10,20,50,100与200,保持SNR固定为10 dB,其他仿真条件保持不变。在每个快拍数下做200次Monte-Carlo实验,上述4种算法的RMSE统计结果如图2所示。

从图1与图2中所示的仿真结果中可以看出,上述4种DOA估计算法随SNR和快拍数的增大,估计精度都有所提升。不过,MUSIC算法的估计精度受SNR与快拍数的影响最大,在SNR较低以及快拍数较小时,MUSIC算法的估计精度最低。而随着快拍数和SNR的增大,由于网格失配问题的存在,导致MUSIC算法的估计精度要优于l1-svd算法。

ANM算法以及本文所提出的M-FIPM算法,对SNR以及快拍数的鲁棒性更好,同时能够解决网格失配问题,所以在相同的仿真条件下,估计精度要高于MUSIC算法以及l1-svd算法。而M-FIPM算法在降维过程中由于舍弃了协方差矩阵中的小特征值分量,对噪声进行了抑制,所以在估计精度方面还要优于ANM算法。

然后,通过仿真实验来验证IPM、ADMM以及M-FIPM 3种SDP问题求解算法的求解效率。而算法的求解效率主要由收敛速度以及每次迭代的算法复杂度所共同决定。

在算法复杂度方面,IPM算法每次迭代的复杂度为O(M6),而ADMM算法以及M-FIPM算法每次迭代的复杂度均为O(M3)。因此,本文所提出的M-FIPM算法在复杂度方面具有显著优势。

在算法收敛速度方面,SDP问题求解算法的收敛速度主要体现在算法达到收敛时所需要的迭代次数。因此,本文通过对比在不同的SDP问题维度下,上述3种求解算法达到收敛时的迭代次数来验证所提出M-FIPM算法在收敛速度方面的性能。

实验 3固定SNR为10 dB,快拍数为200,阵元数由10均匀变化至50,步长为10。其他仿真条件与前文的仿真实验相同,在每个阵元数下做200次Monte-Carlo实验,收敛时上述3种算法平均迭代次数的统计结果如图3所示。

从图3中所示的仿真结果中可以看出,ADMM算法达到收敛时所需要的迭代次数远高于IPM算法以及M-FIPM算法。而M-FIPM算法达到收敛时所需要的迭代次数虽然要略高于IPM算法,但根据前文所分析的结果,M-FIPM算法每一次迭代过程的算法复杂度要远低于IPM算法,所以M-FIPM算法的求解效率依然要优于IPM算法。

在图4中,给出了在不同阵元数下,上述3种SDP问题求解算法的平均运行时间。而该实验结果也验证了本文之前的结论,即M-FIPM算法具有最高的求解效率,在SDP问题的维度相同时,所需的运算时间最短。

最后,对比MUSIC、l1-svd、ANM以及M-FIPM共4种DOA估计算法的平均运行时间。在不同阵元数下,做200次Monte-Carlo实验,统计上述4种算法的平均运行时间,统计结果如图5所示。从图5的仿真结果中可以看出,在相同的仿真条件下,MUSIC算法的运算速度最快,l1-svd算法的运算速度最慢,而本文所提出的M-FIPM算法,在平均运行时间方面,要优于ANM算法。

5 结 论

针对现有快速内点法仅适用于单快拍模型的缺陷,本文提出了一种多快拍快速内点法。该算法利用天线阵列接收多快拍数据协方差矩阵的特征向量加权和来构造适用于原子范数最小化理论的观测模型,然后将DOA估计问题转化为SDP问题,并最终通过Toeplitz矩阵的Vandermonde分解获得最终的DOA估计结果。仿真实验验证了该算法在估计精度与运行时间方面的优势。