无人机集群牵制控制系统特征值分析

刘锦涛, 何 明, 罗 玲, 柳 强, 禹明刚

(陆军工程大学指挥控制工程学院, 江苏 南京 210007)

0 引 言

无人机集群是由一定数量的无人机共同组成,以交感网络为基础,整体具有能力涌现特点的空中移动多智能体系统。相比于追求将所有功能集成于一身的传统飞行器,无人机集群具有多智能体系统的诸多优点,如感知与执行的分布式与并行性、冗余性、容错性、单个成本的低廉性及整体功能的涌现性。尤其是近年来随着计算机技术、无线移动网络技术、控制技术、多智能系统理论、复杂网络科学的迅猛发展,以协同飞行控制为核心的无人机集群已成为飞行器发展的新趋势。当前,各军事强国普遍认为无人机集群作战将是未来颠覆性的作战样式,也是通信、网络、控制和机器人等学科重要的研究方向。

传统的无人机指挥控制多采用集中控制模式,指挥控制站收集一个或多个无人机数据,运行相应算法并将命令发送回执行器。虽然集中控制在理论上可以达到最优的系统性能,但考虑到射频无线电通信易受干扰以及通信隐蔽性等限制,这种策略在军用无人机集群中是难以满足的,另外计算资源、通信带宽、控制延迟等限制,也是制约集中控制模式的因素。所以无人机之间只能使用局部信息(可通过视觉系统、近距离紫外光通信获得周围无人机的信息)。因此,分布式控制策略是更实际的解决方案。相对于集中控制模式,它基于局部信息以及本地控制器的计算可实现次优性能,优点是具有更高的鲁棒性和可行性。此时,地面指挥控制站只需要选择无人机群的一小部分甚至其中一架作为领导者,对其实施直接控制,而其他无人机则通过无人机之间的协同规则实现间接控制。

蜂群中只需要少量的个体(5%)就能引导整个群体飞到新的巢穴中,受此启发,有学者提出了牵制控制的集群控制方法。牵制控制方法对于无人机集群、无人车集群等工程系统具有非常好的应用价值,通过向集群部分节点发布控制指令并采用牵制控制方法,可引导集群朝着预定的目标运行。早在2006年,Olfati-Saber构建了比较完整的蜂拥控制算法框架,设计了有领导者、无领导者和障碍环境中的蜂拥控制算法。不足之处是Olfati-Saber方法假设所有成员都能获取虚拟领导者的位置和速度信息,这其实需要全局通信,在实际过程中是难以实现的。在随后的研究表明,当只有一小部分节点被告知虚拟领导者的状态时,蜂拥控制也是可以实现的,即可以通过牵制控制实现集群的蜂拥控制。通过这种方式,不知情的成员可以由知情的成员驱动,因此集群只需要更少的通信成本。但是文献[8]没有提供牵制节点选择算法,也没有给出应该通知哪些节点的明确规则。在牵制控制节点选取方面,最少节点集合的选取是一个NP-hard问题,目前尚无最少控制节点集的直接求解方案。分布式控制系统的性能不仅取决于本地控制参数,还取决于牵制节点的选择以及控制网络的结构。当无人机集群处于某一个确定的拓扑结构时,为了找到一个数量最少的输入控制节点集合实施控制,使整个系统是结构可控的,是近年来研究的一个热点问题。

本文通过分析蕴含图的结构特性的Laplace矩阵的谱,尤其是,其大小直接反映了图连通性、鲁棒性甚至是集群分布协同控制的收敛性。通过施加牵制控制,进一步将Laplace矩阵变为增广Laplace矩阵。通过估计的特征值的大致范围以及牵制控制造成特征值的变化趋势,可以初步得到牵制控制对系统的收敛性影响。

1 基于矩阵谱的分析方法

Laplace矩阵的谱包含有关图的结构特性的信息,包括它的连接性(用不等式表示)和生成树的个数(用恒等式表示),当增加或删除边时,Laplace矩阵的谱同样会随着图形的结构变化而变化。尤其是的大小直接反映了图连通的鲁棒性,甚至是集群分布协同控制的收敛性。

相关研究有,文献[16]提出了一种基于邻接矩阵谱的子图中心性度量方法。文献[17]提出了一种基于谱的中心性度量方法,对节点在牵制控制中的重要性进行评价并排序。文献[18]提出扰动策略的节点删除方法,通过一定顺序删除节点以增大图的谱间隙(即第1个Laplace矩阵的最小特征值)以增强网络的一致性和收敛性能。在文献[19]引入了一种新的度量方法,根据节点从网络中移除时对网络同步性产生的影响对节点进行排序。

文献[20]定义同步指数为

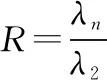
(1)

式中:是Laplace矩阵的特征值比,即最大特征值除以第二小特征值。特征值比越小,网络的同步性能越好。另外,该方法只需要求解Laplace矩阵的两个特征值,计算简单。

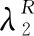
定义Laplace矩阵最大特征值和第二小特征值的变化为

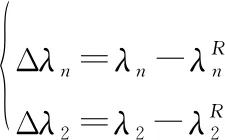
(2)

进一步地将节点的移除所引起的变化表示为

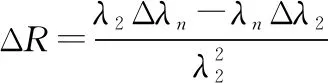
(3)

值得注意的是,由于远比大,因此Δ受Δ的影响要远大于Δ。因此,当删除一个节点,如果对Δ的影响最大,通常对Δ的影响也将是最大的。

从复杂网络中删除一个节点可以建模为删除Laplace矩阵的相关行和列,以及减少对角项中代表其他节点与此节点相连接的数目。对于大规模网络,单个节点的移除,这种扰动几乎可以忽略不计。因此,通过去除Laplace矩阵的第行和第列来近似去除节点的效果。如果去掉该节点而引起的Δ值很小,认为该节点对网络的同步性不太重要。Laplace矩阵的同步指数,是表征网络同步性的一个重要指标,同步指数越小,网络的同步性能越好。同步指数越小表明Laplace矩阵最大特征值和次小特征值 的比值很接近于1,进而表明Laplace矩阵的所有特征值几乎都相等。

2 系统模型

2.1 无人机集群动力学模型

图论和矩阵论是对复杂网络进行定量分析的数学基础,为了进一步从数量的角度描述无人机集群行为,基于图论框架进行建模分析,是当前最为简洁有效的分析方式,再进一步将图模型转换为矩阵方程,可以建立起复杂网络与控制理论诸多联系。

本文主要考察通信拓扑对无人机集群控制的影响,如图1所示,假设无人机集群包含,,…,,架无人机,它们具有有限范围的感知区域。(通常无人机之间通过无线通信进行信息交流,也可以通过机载雷达、视觉等传感器获取周围无人机状态信息,如文献[22]在无线电静默条件下,通过使用视觉传感器实现了蜂拥飞行。)将单个无人机抽象为一个节点,无人机之间的交互抽象为节点之间的连线,如图1中实线所示。另假设黑色方块为地面指挥控制站,且仅与部分无人机联络通信,如图1中虚线所示。所有无人机节点组成一个顶点集={,,…,},假定无人机通信链路是双向的,将它们之间的联系抽象为边。定义边集合,如果{,}存在连接关系则{,}∈⊂[]。最终,无人机集群可抽象为一个无向无环简单图={,,}。指挥控制站向集群发布控制指令为虚拟领导者的位置与速度,引导无人机集群飞往预定目标。

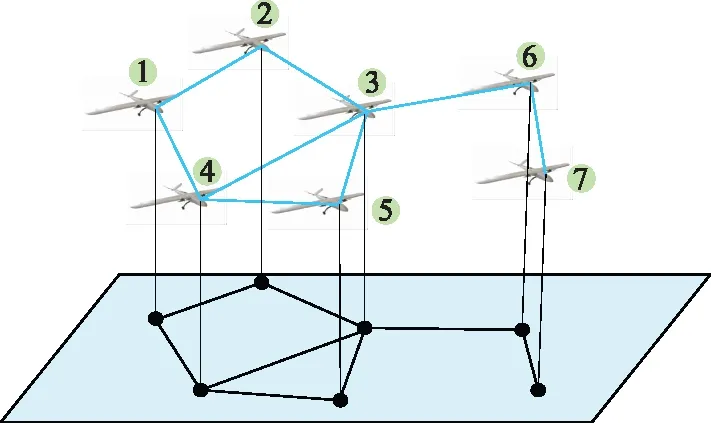
图1 无人机集群的图映射Fig.1 Graph mapping of unmanned aerial vehicle swarm

不失一般性,忽略无人机自身动力学特性,将无人机抽象为三维运动的质点。

考虑个无人机工作在维欧几里得空间上,其质点运动学方程为

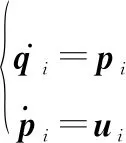
(4)

式中:,,∈分别为无人机的位置向量、速度向量和加速度向量,=1,2，…,。

时刻无人机集群构成的无向图()由节点和边组成,其中节点集合用={1,2，…,}表示,边的集合用()={(,)∈×,∈()}表示。设是无人机集群的感知半径,期望距离为,则无人机邻域定义为

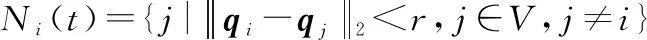
(5)

无人机集群网络可以使用Laplace矩阵表示。Laplace矩阵定义为

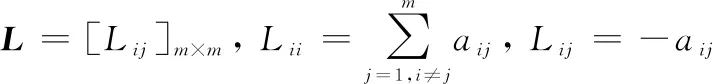
(6)

式(6)中,仅当∈,=1,否则=0。

满足下列平方和性质:

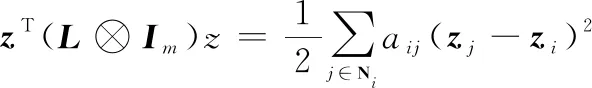
(7)

为避免个体间发生碰撞,规定无人机集群系统的期望演化目标为

‖-‖=, (,)∈;<

(8)

并将式(8)命名为-lattices系统。但由于个体之间的吸引力和排斥力的相互作用,会导致难以达到理想的-lattices,最终演变为

-+≤‖-‖≤+, (,)∈

(9)

式(9)被称为类-lattices系统。

2.2 控制器设计

设时刻控制输入为

(10)

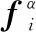
(11)

式中:=sign(-)为期望间距控制项。当期望距离=0时,式(11)由蜂拥问题退化为二阶一致性问题。将sign函数按照坐标进行分解。

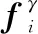
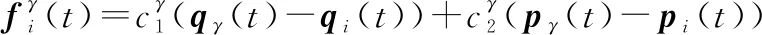
(12)

式中：∈为时刻虚拟领导者的速度向量;()是与牵制节点的选择和时间相关的参数,时刻()的数学表示为

=diag(,,…,)

定义增广Laplace矩阵

=+k

(13)

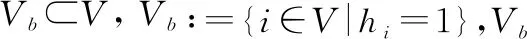
无向图初始状态(0)是连通的。若初始状态不是连通的,分为个子网,则每个子网至少有一个牵制点,可得到相同的结论。

初始状态无碰撞。

虚拟领导者速度固定。

考虑一个无人机集群运动方程如式(1)所示,控制输入如式(6)所示,则任取一个或多个节点作为牵制节点,均有:

(1) 所有无人机相对位置最终会趋向lattices;

(2) 所有无人机速度会趋向虚拟领航者速度()(对文献[25]速度一致性证明的改进);

(3) 无人机之间不会发生碰撞;

(4) 牵制节点位置会趋向虚拟领航者位置()(对文献[26]位置结论的拓展)。

3 牵制点对系统特征值的影响

通过分析蕴含图的结构特性的Laplace矩阵的特征值,尤其是,其大小直接反映了图连通性、鲁棒性甚至集群分布协同控制的收敛性。通过施加牵制控制,进一步地将Laplace矩阵变为增广Laplace矩阵,如式(13)所示。通过估计的特征值的大致范围以及牵制控制造成特征值的变化趋势,可以初步得到牵制控制对系统的收敛性影响。

3.1 特征值分析

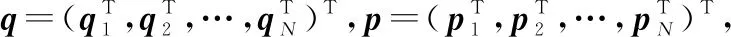
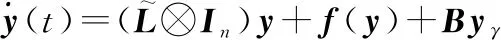
(14)

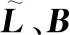
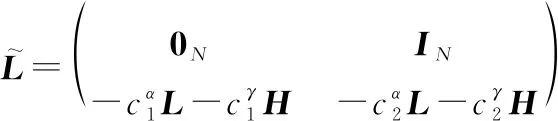
(15)

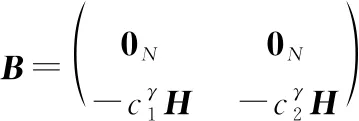
(16)

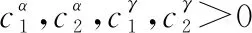
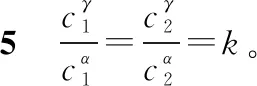
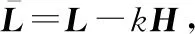
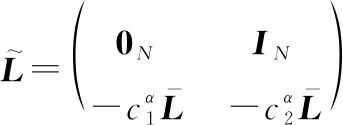
(17)

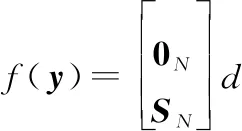
(18)

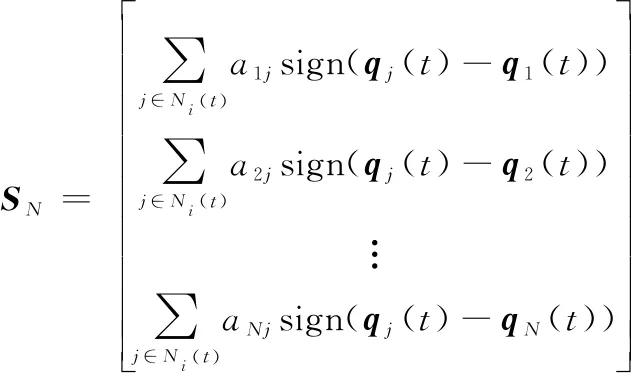
(19)

由于≠,即无人机之间不重叠时,有

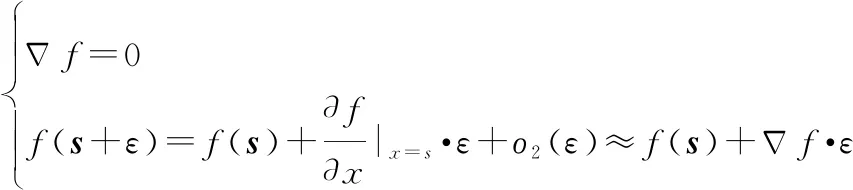
(20)

故可将()视为常值小扰动。

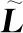
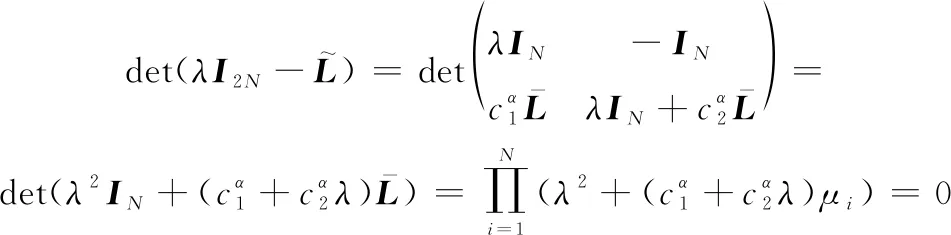
可得

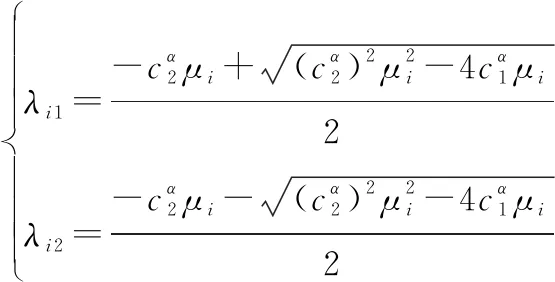
(21)

式中:=1,2, …,。

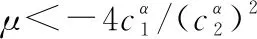
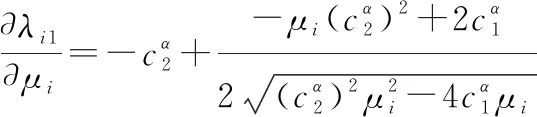
(22)

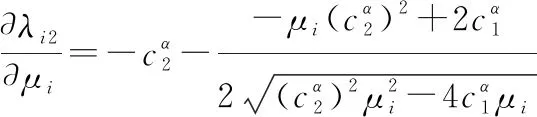
(23)

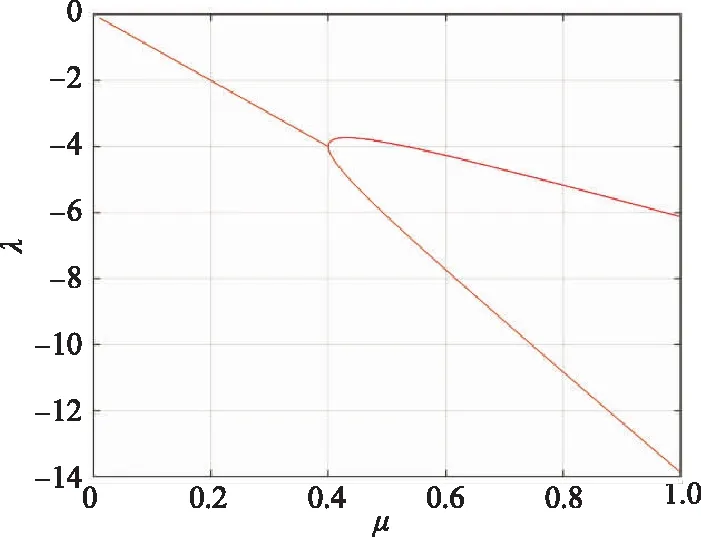
图2 μ对根轨迹实部的影响Fig.2 Effect of μ on the real part of the root locus

使用Matlab Symbolic Math Toolbox计算得:

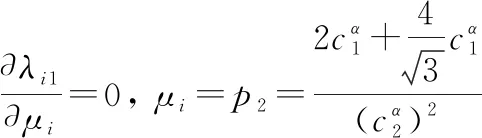
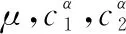
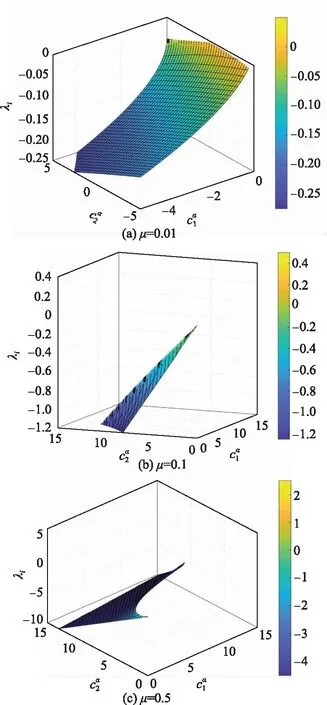
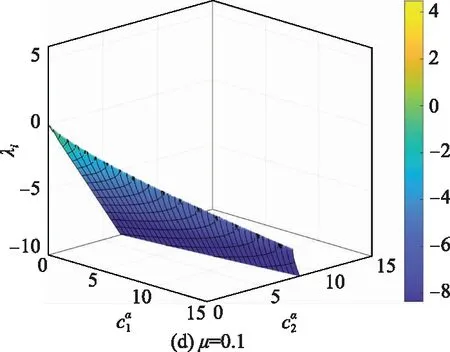
图3 λi与μ,,之间的关系Fig.3 Relationship between λi and μ,,

对于强连通网络,每增加一个牵制控制节点或提高控制增益都可以提升系统的可控性。

在文献[27]中提出一种基于左Perron向量的控制策略,但需要反复迭代计算+k的特征值和特征向量,由于特征值求解计算量大,实际工程中比较困难。可使用特征值摄动的方法对最优牵制点进行近似求解。

对于一阶一致性问题,当不施加牵制控制时,由于Laplace的最小特征值为0,导致无人机集群最终收敛的平衡态不一定为0,取决于无人机集群初始状态的平均值,其第二小的特征值决定一致性收敛速度。当施加牵制控制后,由于系统最小特征值小于零,平衡态最终收敛至牵制点的状态。

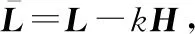
3.2 最小特征值范围估计

分析最小特征值的范围有助于直观了解系统的可控性以及动态性能,接下来用矩阵最小特征值相关结论对的最小特征值进行估计。

首先介绍以下矩阵定义。

()为的最小特征值。

矩阵：非对角元素均为非正数的实数方阵。={=()∈×:≤0 if≠,(,=1,…,)}。

矩阵:如果非奇异矩阵∈,且的所有特征值均为正,则矩阵称为矩阵。

由引理1得,为正定阵,则为矩阵,∈。

估计矩阵的最小特征值的范围是矩阵理论中一个重要的课题,目前已有了许多取值范围日趋精确的研究成果。另外,在实际应用中除了估计精度外,还需要考虑计算的可行性和便捷性,根据文献[34],()在以下范围:

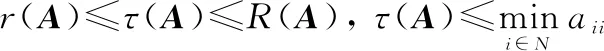
(24)

式中:

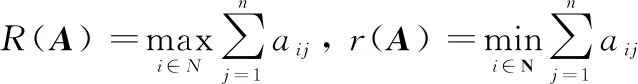
(25)

由于为Laplace矩阵,则有()=0,()=max()。

0<()≤min(max(),min())

令=()∈,=(),可得

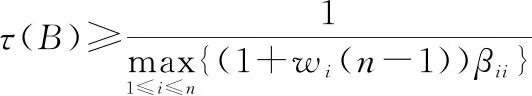
(26)

4 仿 真

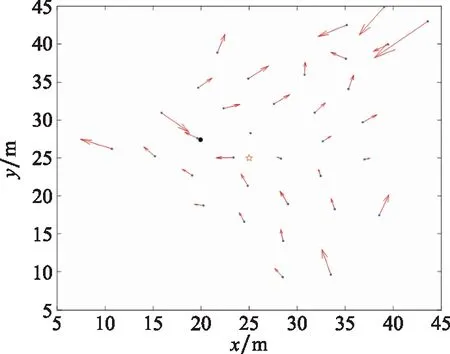
图4 无人机集群初始状态Fig.4 Initial state of unmanned aerial vehicle swarm

将整个无人机集群系统视为一个整体进行分析,定义集群中心(center of mass, CoM)的位置与速度为所有无人机的位置和速度的平均值:

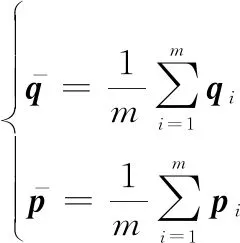
(27)

定义CoM与虚拟领导者的跟踪误差为

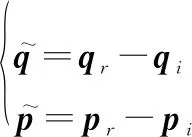
(28)

定义多智能整体速度跟踪误差为

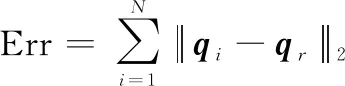
(29)

定义归一化的平均速度为

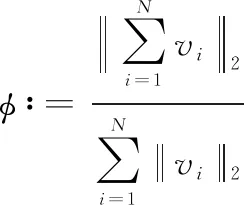
(30)

无人机集群运动轨迹如图5所示,不同时刻无人机集群状态如图6所示,无人机集群跟踪速度误差、分量收敛情况分别如图7、图8所示。无人机集群系统归一化的平均速度误差收敛如图9所示。

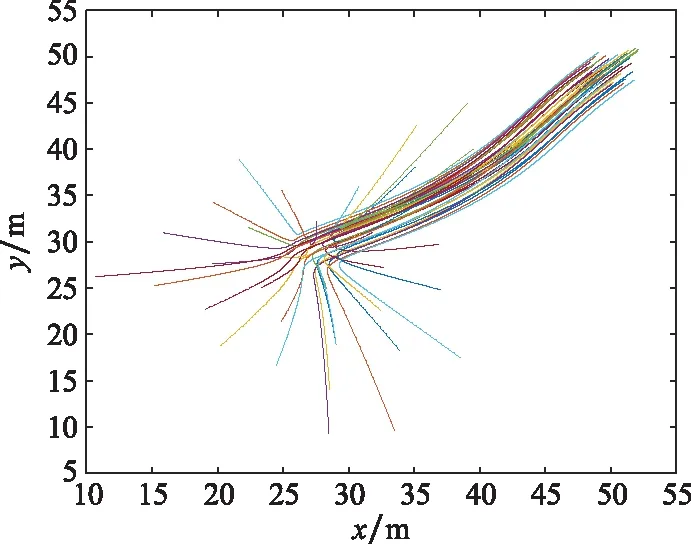
图5 无人机集群运动轨迹Fig.5 Trajectory of unmanned aerial vehicle swarm

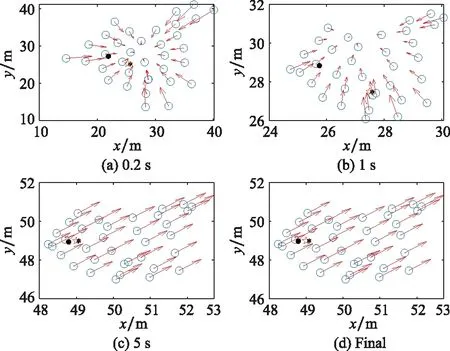
图6 不同时刻无人机集群状态Fig.6 Unmanned aerial vehicle swarm status at different times

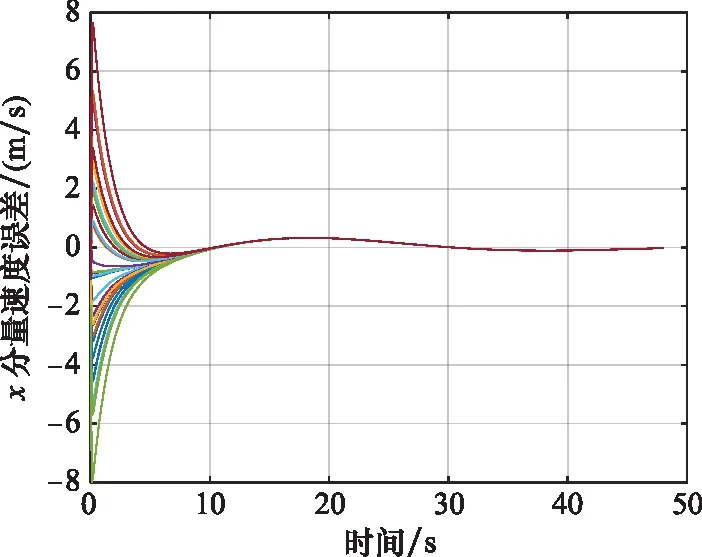
图7 无人机集群跟踪速度误差x分量收敛情况Fig.7 Convergence of x-component of unmanned aerial vehicle swarm tracking speed error

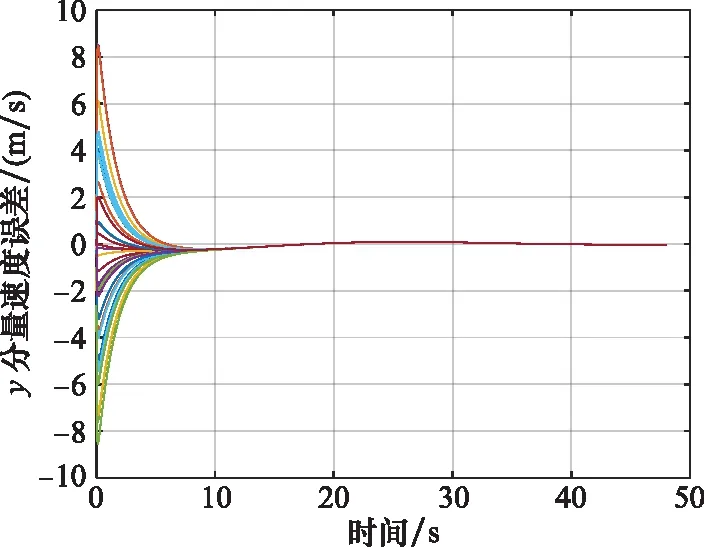
图8 无人机集群跟踪速度误差y分量收敛情况Fig.8 Convergence of y-component of unmanned aerial vehicle swarm tracking speed error

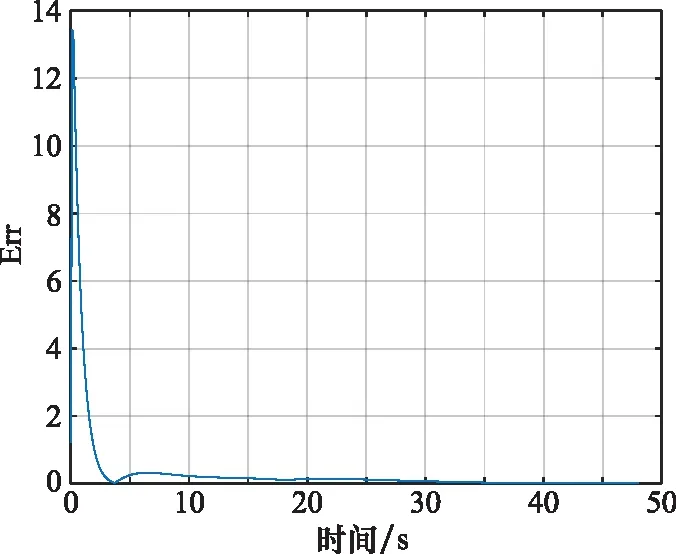
图9 无人机集群系统总体速度误差收敛情况Fig.9 Convergence of general velocity error of unmanned aerial vehicle swarm system

从仿真来看,文中所给出的算法能够实现有效的蜂拥控制。所有的无人机速度很快实现基本一致,并逐渐趋近于虚拟领导者的速度,无人机之间的距离随着时间的变化逐渐接近于理想距离,并且一直大于0,验证了定理1的正确性。当实现了蜂拥运动后,无人机与虚拟领导者的速度跟踪误差将与牵制点的选择没有直接关系。

5 结 论

使用牵制控制对集群蜂拥形成速度的影响是显著的,本文初步从Laplace特征值的角度分析了牵制控制对系统的收敛性影响,构建了增广Laplace矩阵,并估计了系统特征值的范围。在未来需要进一步定量分析在某一节点增加牵制控制对系统特征值以及一致性收敛的影响。结合任务需求、无人机具体的动态特性以及飞控系统做进一步应用研究。