精创模型建构策略 强化模型意识培养

浙江衢州市柯城区白沙小学（324000）蒋小芬

小学生的数学学习要着重关注模型意识，而经历模型建构的过程才能强化模型意识的培养。

模型建构可以从学生熟悉的生活和已有的经验出发，引导他们将实际问题初步抽象成数学模型并加以解释与运用。经历模型建构过程，学生将感悟数学与现实世界的密切联系，学会用数学的眼光观察世界；针对或参照某种事物系统的特征或数量依存关系，进行分析、抽象、简化，提炼数学本质特征，学会用数学的思维思考世界；学会用数学的语言，以及采用多种形式的数学语言描述世界。

一、模型建构的现状

目前，学生对模型建构存在习得性问题。笔者在实际教学中收集了学生在应用模型时出现的问题，并从四个知识领域进行分析归类（如表1）。

表1 学生模型建构的三类习得性问题

续表

二、数学模型建构的有效策略

如何结合学生学习的难点与困惑，让学生有效地体验模型建构、增强模型意识？如何促进学生对数学模型的深度理解？笔者从以下方面进行了有效的尝试与实践。

1.精选问题，挖掘建模素材

（1）生活化+冲突化，唤醒建模意识

生活背景是数学建模的基础，用数学的眼光观察生活情境并发现和提出问题是数学建模的起点。因此，教师可以从学生熟悉的生活背景中甄选素材作为基本内容，让学生激活并提取数学模型的逻辑雏形，在真实情境中揭示数学本质。选择思维冲突化的问题情境，更能激发学生的思考欲望，使学生主动求变、求通，充分激发学生的主观能动性，以此唤醒学生的模型意识。

【案例】减法的性质

学生学习减法的性质a-（b+c）=a-b-c和a-（bc）=a-b+c时会产生这样的认知冲突：为什么去掉括号后加减运算就变了呢？教师可借用以下生活实例唤醒学生的模型意识（如表2）。

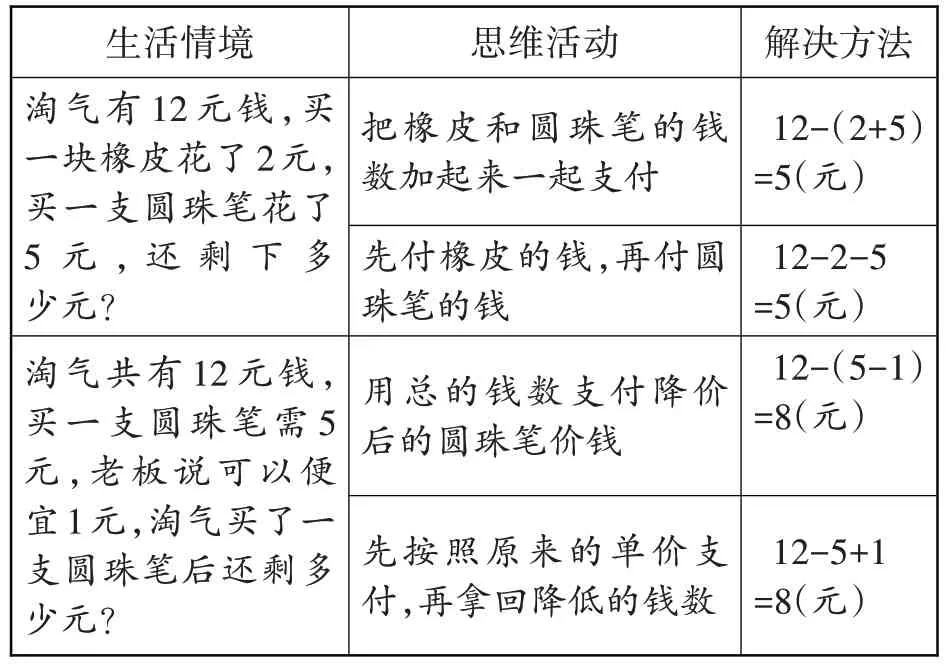
表2 减法性质的学习素材

通过具体实例唤醒学生的建模意识，并使学生在认知冲突中比较两个模型，学生原先的认知失衡便会转变为认知平衡。

（2）直观性+类比性，助推建模体验

数学模型的建构需要数学活动作为载体，所以教师要给学生提供直观性、结构性、类比性、全方位的材料，助推建模活动，增强学生的建模体验。

【案例】相交与平行

笔者收集学生绘制的两条直线的关系图，有五种情况（如图1）。

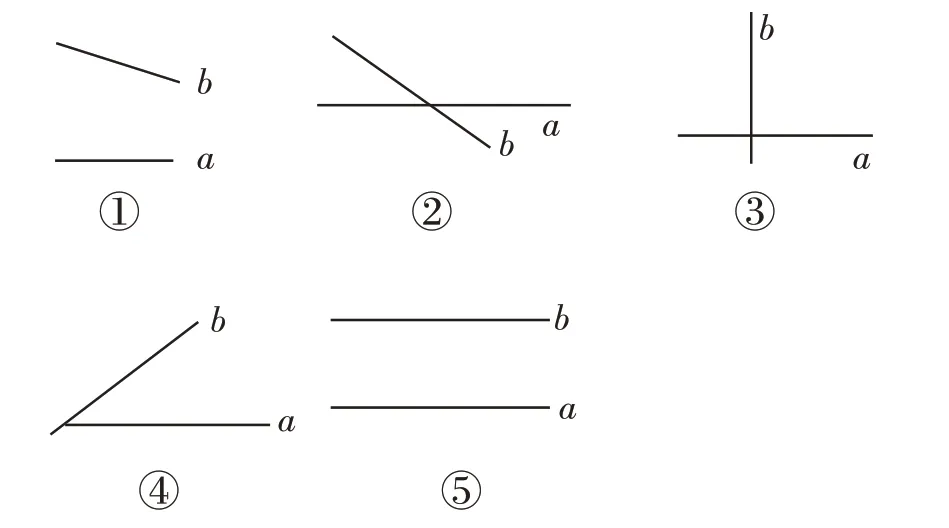
图1

学生先分小组讨论直线的位置关系，再记录分类理由，最后全班聚焦到一个问题上：①号作品中的两条直线究竟有没有相交？学生纷纷阐述观点“不相交，因为没有‘交’。”“会相交，因为直线是可以无限延长的，当延长到一定程度后这两条直线就会相交。”学生动手展示延长直线的过程，证明①号作品中的两条直线最后会相交。

①号作品利用看似没有交点的两条直线引发学生的讨论，使学生经历“推测—讨论—动手验证”的过程，并由此进入深度学习的状态，增强了模型建构的体验。

2.紧扣思维，推进建模进程

（1）聚类中抽象，模型螺旋成形

数学模型并非针对单个数学现象或者数学特征，其本质上具有典型的“类”的特征。因此，教师要为学生呈现丰富的表象，将概念简单化、整体化，促进模型的建构。

【案例】正比例

笔者汇聚“差不变”“乘积不变”“比值不变”三类变量实例，通过抽象、概括、辨析来引领学生认识正比例的概念，将建构正比例概念模型分成了三个层次。（如图2）

图2

第一个层次的认识是“变量”，即能在以上三类变量的具体情境中，体会两个变量存在联系。第二个层次是认识正比例中两个变量的变化方向：一个量增大另一个量也随之增大。第三个层次是最终认知节点：两个变量变化方向一致的同时，扩大或缩小的倍数也一样，即两个变量的比值不变，从而抽象出正比例的概念。

通过三类不同的变量类型，学生经历了“相关联—变化方向—比值一定”的抽象过程，最终顺理成章地建构正比例的概念。这也为后续反比例概念的教学奠定抽象、比较、符号化等建模基础。

（2）思辨中提炼，完善模型建构

课堂教学只有考虑学生的立场和整体视角，以及学生的学习难点、困惑点，才能更有效地帮助学生在思辨异同的过程中提炼本质特征，提高建模意识，逐渐完善模型的建构。

【案例】“平行”的概念教学

教师出示以上三个正方体，并提出以下问题。

①正方体a，同一个平面上的直线：

问题：任选一个面，你能找到两条互相平行的直线吗？

②正方体b，异面的直线：

问题：观察l1，l2，这两条直线，它们互相平行吗？为什么？

如果一元二次方程ax2+bx+c=0(a≠0)有两个实数根x1和x2，那么这就是著名的韦达定理.现行义务教育初中数学教材中的证法是利用一元二次方程ax2+bx+c=0的求根公式先求出它的两个根，然后分别计算这两根之和与两根之积.笔者在文[1]中不借助于一元二次方程的求根公式给出了韦达定理的三种代数证法,本文再给出韦达定理的三种几何证法,供大家参考.

③正方体c，看似异面实则共面的直线：

问题：l3，l4，这两条直线互相平行吗？这两条直线所在的面隐藏在哪里？

最后展示平移直线，动态生成第三个平面：

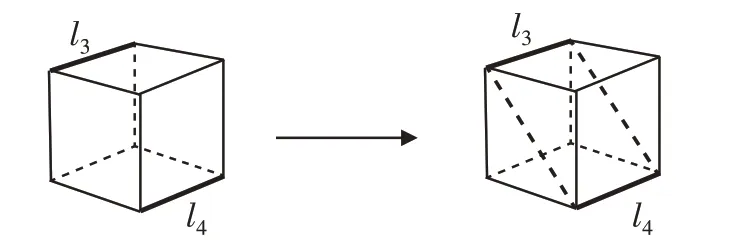
图3

此案例中，学生充分经历同一个平面、异面的两条直线位置关系的辨析过程。在同一个平面上，不相交的两条直线互相平行；在异面上，不相交的两条直线有时平行，有时不平行，如果直线l3经过平移可以与直线l4完全重合，那么平移l3所扫过的区域就是这两条直线共属的平面。在对看似异面实则共面的直线的辨析过程中，学生实现了深度思考，逐渐完善“在同一个平面内，两条永不相交的直线互相平行”的数学模型。

3.与“实”俱进，延伸模型实践

（1）结合实践经验，引导建模应用

学生建立数学模型后，最终要在生活实际中验证数学模型的可行性，并应用数学模型去解决实际问题。

【案例】圆柱的表面积

问题：有一种圆柱形的茶叶罐，要对其进行包装，为了尽可能地避免浪费，应该选择怎样的包装方式？

问题：给一根底面周长为3.14平方分米、高为3.8米的柱子刷油漆，每平方米要刷0.7千克油漆，共需要多少油漆？

问题：制作100个烟囱需要多少平方米的铁皮？

学习了圆柱的表面积后，学生已经建立了丰富的表象，并初步建立了模型。为了实现更深刻的认知，教师可引入生活实际问题，强化学生的应用意识，帮助学生积累数学应用的经验，使学生加深对数学模型的理解，体会数学模型的价值。

（2）积累数学化经验，养成建模习惯

建构数学模型需要学生将问题数学化，用文字、图形或者符号表达数量关系和一般性特征，形成建模的习惯。比如，在解答图2中的“乐乐和爸爸的年龄”等问题时，学生能主动地用简单的符号来表达不同的关系（如表3）。

表3 不同变量关系的数学语言表达

学生运用数学语言表达数量关系，不但能养成用数学眼光看待问题的习惯，而且能在知识的梳理、反思学习中领会模型思想，不仅有效地解决了问题，还为后续学习打下了坚实的基础，形成了良好的数学核心素养。

（3）渗透模型意识，延伸数学思维

学生在经历建构模型的过程中不仅要掌握建模方法，还要主动追溯问题的核心和本质，从形式上、方法上、思想上去延伸数学思维。

针对圆柱的表面积问题，教师可出示延伸数学思维的问题串，以引发学生对数学知识本质的思考：回顾一下，我们已经掌握了哪些图形的表面积计算方法？你能画出这些图形的侧面展开图吗？能用公式表示这些图形的侧面积的计算方法吗？它们之间是否存在相同点？

将学生思维局限于课堂并不能真正起到培养学生模型意识的作用，所以教师可以将学生思维延伸到课外，引导学生提炼数学问题，组建项目化学习小组，关注自主学习过程，如此才能达到持续探究的目的。

值得注意的是，模型意识的培养也应做到以生为本。教师长期坚持强化学生数学模型意识的培养，使学生逐渐学会用数学的眼光去看待问题、分析问题，感受现实生活中蕴含着的大量数学知识，并能运用数学知识将生活问题抽象、建构成数学模型，从而能从解决一个数学问题到解决一类数学问题，再到解决一般现实问题，形成模型观念。