基于遗传算法的临水加筋土挡墙拟静力内部稳定分析

侯超群，檀 奕，阮晓波，陈 欢

(合肥工业大学 汽车与交通工程学院，安徽 合肥 230009)

0 引言

加筋土挡墙由于具有经济、安全以及施工方便等优点，在水利、交通、城建等领域得到了广泛的工程应用。在地震荷载的作用下，相比传统的挡土结构，加筋土挡墙能表现出良好的抗震性能[1]。临水边坡由于受到水位的影响，土体强度存在较大的变异性，在地震作用比一般边坡更易发生失稳，因此在地震频发地区采用加筋土挡墙作为临水护岸结构，可以利用其抗震性能，达到工程应用的安全性。

地震作用下加筋土挡墙的内部稳定分析是其工程设计中的必要环节。地震作用下加筋土挡墙的计算方法有：拟静力法、拟动力法以及数值分析法等[2-5]。拟静力法是将地震惯性力视为自重与地震加速度系数的乘积，并将其施于墙后不稳定体上进行极限平衡分析[6]。拟动力法考虑地震频率等因素，基于弹性波理论来求解土体中的剪切波和压缩波的波速，从而得到水平和垂直

加速度沿墙高的分布方程，并通过建立平衡方程得到地震力[7]。数值模拟法用计算机模拟地震作用下土体本身强度变化和破坏过程，具有易于建模以及能够反复操作的优点[8]。当前的设计规范一般简化滑裂面形式，基于极限平衡原理采用拟静力法进行加筋土挡墙的抗震设计。Choudhury和Ahmad[9]、黄睿等[10]基于拟静力法和水平层分析法假定滑裂面为直线型和折线型对临水加筋土挡墙进行内部稳定分析。Terzaghi[11-12]研究表明，假设滑动面为直线和折线型，所计算得到的筋材拉力系数会偏大，计算误差有时可达到2～3倍，甚至更大。通常，挡墙计算中简化破裂面为直线型和折线型等形式，但采用对数螺旋线破坏机制更加符合实际。

在已知破裂面形式的基础上，建立平衡方程，求得结构破坏的最危险滑裂面，也就意味着获得了安全系数(对于边坡稳定分析)、土压力(对于挡土墙设计)或者所需筋材拉力(对于加筋土挡墙内部稳定分析)的极值。采用智能搜索方法是确定最危险滑裂面的一种重要途径。人工智能算法搜索效率高、不易陷入局部极值，并且易与其他算法相结合。目前在临界滑动面搜索中的人工智能方法有遗传算法、模拟退火算法和仿生算法等[13]。其中，遗传算法通用性强、全局搜索能力强，且不需要梯度信息、不要求函数连续，适合于并行处理和大型复杂优化问题的求解。

本研究假定破裂面是对数螺旋线，基于极限平衡原理和拟静力方法，建立地震荷载作用下临水加筋土挡墙内部稳定分析的力矩平衡方程；进而采用遗传算法确定临水加筋土挡墙的最危险滑裂面，获得其内部稳定设计的所需筋材拉力；最后分析地震荷载作用下超静孔压、水位高度、填土内摩擦角等因素对临水加筋土挡墙筋材拉力的影响。

1 基本力学模型

1.1 基本假定

(1)墙后填土为各向同性的均质无黏性土。

(2)假设破裂面是对数螺旋线状。

(3)假设破裂面通过墙趾。

(4)已知沿着挡墙高度的筋材拉力的分布函数。

(5)墙后填土具有较高的渗透性，水可以在土体中稳定渗流，在发生地震时填土侧产生动水压力。

图1 临水加筋土挡墙力学模型Fig.1 Mechanical model of waterfront reinforced retaining wall

1.2 受力分析

临水加筋土挡墙的力学模型如图1所示。墙后填土处于浸水状态，滑动土楔体受到的力有：水平地震惯性力Qh，竖直地震惯性力Qv，土体自身重力W，以及地震引起的动水压力Pd1，Pd2。

1.2.1 地震惯性力

本研究运用Mononobe-Okabe法[14]计算地震惯性力，用土体的自重和地震加速度系数的乘积表示滑动土楔体受到的地震惯性力。地震惯性力Qh，Qv包括水位线以上的干土受到的地震惯性力Qhd，Qvd和水位线以下的湿土受到的地震惯性力Qhs，Qvs。

(1)

式中，kh，kv分别是水平、竖直地震惯性力系数；Wd为干土质量。

根据Matsuzawa.et al[15]的研究，在土的渗透性较强时，水平地震惯性力只考虑作用于填土颗粒上的部分。因此，湿土部分的水平地震惯性力为Qhs=khWd；竖向地震惯性力为Qvs=kvW*，其中W*为用于计算浸水部分竖向地震惯性力的填土重度[2]。

W*=(γsat-γw)(1-ru)Ar，

(2)

式中，γsat为填土的饱和重度；γw为水重度；Ar为滑动土楔体浸水部分的面积；ru为地震超静孔压与竖向有效应力的比值。

1.2.2 水压力

浸水部分的填土受到的水压力有：静水压力和动水压力。由于本研究假设填土两侧水位高度相同，故静水压力相互抵消，不加以考虑。

根据Westergaard法[16]，作用于滑动土楔体临水侧与填土侧的动水压力为：

(3)

式中hw为水位高度。

1.3 力矩平衡方程

Leshchinsky和San在前人的基础上，通过变分极限平衡法研究了土质边坡拟静力条件下的对数螺旋线破坏机制及稳定性设计[17]。本研究采用该破坏机制建立临水加筋土挡墙内部稳定受力计算模型，如图1所示，其中对数螺旋线半径为：

R=Ae-ψmβ，

(4)

通过几何关系，可以确定滑裂面在直角坐标系中的方程，如下：

(5)

式中，A=H/(e-ψm β1cosβ1-e-ψm β2cosβ2)，是对数螺旋线常数；β1，β2分别为滑裂面上E，F点对应的极角；ψm=tanφ/FS，FS=1.0，为安全系数；φ为墙后填土内摩擦角；β为对应计算点的极角；(xC,yC)是对数螺旋线极点C点所对应的直角坐标。

(6)

滑动土楔体在极限平衡状态下，外力绕极点C产生的力矩平衡，即：

M∑Ti=MG+Mkh-Mkv+MPd1+MPd2，

(7)

式中，MG，Mkh，Mkv，MPd1及MPd2分别为滑动土楔体受到的重力、水平地震惯性力、竖直地震惯性力、临水侧动水压力及填土侧动水压力绕C点的力矩。

(1)重力力矩：滑动土楔体重力绕(xC,yC)点的力矩分为干土和湿土两部分进行积分；力臂为Ae-ψmβsinβ。求得滑动土楔体重力力矩MG见附录。

(2)地震惯性力力矩：水平和竖直地震惯性力绕(xC,yC)点的力臂分别为：

(8)

滑动土楔体水平、竖直地震惯性力力矩Mkh，Mkv见附录。

(3)动水压力力矩

(9)

临水侧动水压力绕(xC,yC)点力矩MPd1如上式所示，动水压力合力作用在0.4hw处[18]。

填土侧动水压力绕(xC,yC)点力矩MPd2由填土侧动水压力水平分力和竖直分力积分求得，

MPd2=MPdx+MPdy，

(10)

式中，MPdx，MPdy分别为填土侧动水压力的水平分力和竖直分力绕(xC,yC)点的力矩。MPdx,MPdy的表达式见附录。即可求得筋材拉力合力：

(11)

式中，D为筋材拉力合力作用点的高度，当筋材线性分布时：D=H/3,筋材均匀分布时：D=H/2。其中H为挡墙高度。

1.4 筋材拉力系数

采用无量纲化方式定义临水加筋土挡墙的拉力合力系数为：

KT=∑Ti/(Wd+W*)。

(12)

2 内部稳定的遗传算法分析

传算法(Genetic Algorithm，GA)是一种通过模拟自然进化过程搜索最优解的方法，采用概率化的寻优方法自动获取和指导优化的搜索空间，自适应地调整搜索方向，通过对当前群体施加选择、交叉及变异等操作产生新一代群体，并逐步使群体进化到最优解状态。

2.1 遗传算法的计算过程

应用遗传算法解决实际问题时，首先要建立适应度函数，然后根据遗传算法的基本步骤求解问题的最优解。

(1)目标函数的确定。以(11)式为目标函数，即Rt=∑Ti。Rt的值越大，表示其适应性能越好。

(2)初始化种群。采用二进制编码，随机产生一定数量的染色体，第j条染色体代表向量[β1j,β2j]，并且β1j，β2j满足约束条件：

(13)

(3)适应度函数。适应度函数反映每一代个体对环境的适应能力，即适应度值越高的个体被遗传到下一代的可能性越大。本研究求解挡墙筋材拉力的最大值，即设适应度函数为：

F=Rt=f(β1j,β2j)，

(14)

(4)选择操作。轮盘赌选择是一种回放式随机采样方法，是遗传算法中最常用的一种选择方法，指某一个体被遗传到下一代的概率等于它的适应度值与整个种群中个体适应度值之和的比值。[β1j,β2j]被选中作为父代的概率为：fj=Fj/ΣFj。

(5)交叉操作。按交叉概率pc从群体中随机选择两个个体进行某个或某些位的基因交换，从而产生新个体。交叉概率决定了遗传算法的全局搜索能力，其值越大，收敛速度越快，但当取值过大时，会破坏优良个体，因此将交叉概率pc取0.7～0.9。常用的有单点交叉、多点交叉及均匀交叉等。本研究采用的单点交叉如图2所示，随机地在个体编码串中设置一个交叉点，然后两个配对的个体在该点相互交换部分染色体信息以产生新的个体。

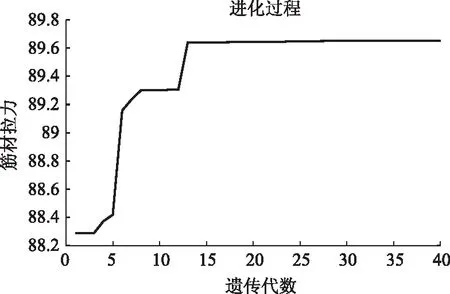
(6)变异操作。变异操作是产生新个体的辅助方法，但也是必不可少的一个运算步骤，它决定了遗传算法的局部搜索能力。将交叉后的子代进行变异操作，以变异概率pm对每个子代重复如下过程：在[0,1]内取随机数r，如果r

图2 交叉操作Fig.2 Crossover operation

2.2 遗传算法的计算结果

运用遗传算法的基本原理和算法程序对地震作用下临水加筋土挡墙筋材拉力的决策变量进行编码，将式(11)作为目标函数，取案例计算中基本参数，设置初始种群数为30，迭代次数为30代，交叉概率pc=0.9，变异概率pm=0.01，对线性布筋的垂直挡墙筋材拉力进行智能寻优。从图3可知，第1代初始种群的最大筋材拉力已达到88.45，与全局最优解89.62已经很接近，在第13代后进化曲线趋于平滑。说明遗传算法具有很好的收敛性。

图3 寻优性能的跟踪Fig.3 Trace of finding best solution

3 案例计算

基本参数：挡墙墙高H=5 m，填土饱和重度γsat=19 kN/m3，填土干土重度γd=16 kN/m3，填土内摩擦角φ=30°，挡墙垂直(α=90°)，kv=kh/2。力学模型如图1所示。

文献[9]假设填土具有较高的渗透性，假定直线型和折线型两种滑裂面，只考虑临水侧静水压力，对浸水部分土体受到的地震惯性力进行折减，计算墙背垂直的临水加筋土挡墙筋材拉力系数。文献[10]根据土的渗透性高低分为水土分算、水土合算两种情况，考虑直线型和折线型两种滑裂面计算墙背垂直的临水加筋土挡墙筋材拉力系数。本研究取相同的参数分别与文献[9]、文献[10]的计算结果进行对比，如表1所示。

表1 本研究方法计算得出的筋材拉力系数KT与其他方法的比较Tab.1 Comparison of tensile coefficient KT calculated by proposed method with those obtained by other methods

从表1可知，在kh=0.1，0.2及0.3时，在挡墙线性布筋时本研究方法分别比文献[9]的筋材拉力计算结果大33.42%，33.62%及38.93%；均匀布筋下分别比文献[9]计算结果大41.24%，37.00%及39.82%。本研究同时考虑临水侧静水压力和填土侧静水压力，文献[9]仅考虑临水侧静水压力，而忽略了填土侧静水压力；由于假设墙后填土具有较高的渗透性，滑动土楔体的浸水部分所受到的水平地震惯性力应仅作用于填土颗粒上[15]，而文献[9]以填土干土重度与平均重度的比值对水平地震惯性系数进行折减后与饱和重度相乘表示浸水部分受到的水平地震惯性力。因此文献[9]的计算结果较小，本研究的计算结果更加合理。

在kh=0.05，0.1，0.15及0.2时，在挡墙线性布筋时本研究方法分别比文献[10]的筋材拉力系数计算结果大2.0%，0.2%，-2.4%及-4.4%；均匀布筋下分别比文献[10]计算结果大9.9%，5.8%，1.8%及-0.9%。可以看出本研究方法计算所得结果与文献[10]非常接近，验证了本研究方法的可行性。

4 参数分析

取上文中的基本参数，考虑墙背垂直(α=90°)、墙背倾斜(α=70°)，筋材线性分布(D=H/3)、筋材均匀分布(D=H/2)，水位高度为hw/H=0.25，hw/H=0.75，填土内摩擦角为φ=30°，φ=40°，超静孔压与填土竖向有效应力的比值为ru=0.3，ru=0.7，水平地震加速度系数kh=0.05～0.2。

4.1 水位高度与墙高的比值

在实际情况中，水位高度是随时发生变化的，但为了简化模型，本研究假设挡墙两侧水位高度相同。取hw/H=0.25，0.75，水位高度对筋材拉力系数的影响如图4所示。在相同墙背倾角、相同的布筋模式和相同地震力作用下，水位高度对筋材拉力系数有增大作用，且对墙背倾斜的挡墙(α=70°)的筋材拉力系数的增大作用较墙背垂直的挡墙更加明显；对均匀布筋的临水加筋土挡墙的筋材拉力系数的增大作用较线性分布更加明显。如在kh=0.1时，从hw/H=0.25到hw/H=0.75，线性布筋和均匀布筋下相对应的墙背倾斜的挡墙(α=70°)的筋材拉力系数KT分别增长66.88%，69.27%；垂直挡墙KT分别增长63.73%，64.58%。此外，hw/H=0.25时，从kh=0.05到kh=0.2，在线性布筋和均匀布筋下相对应的墙背倾斜的挡墙(α=70°)的筋材拉力系数KT分别增长44.71%，34.13%，垂直挡墙的筋材拉力系数KT分别增长26.13%，19.01%；hw/H=0.75时，从kh=0.05到kh=0.2，在线性布筋和均匀布筋下相对应的墙背倾斜的挡墙(α=70°)的筋材拉力系数KT分别增长54.16%，44.38%，垂直挡墙的筋材拉力系数KT分别增长33.48%，25.63%。在其他条件相同的情况下，水位较高时，地震惯性力对筋材拉力的影响更加显著；地震惯性力对墙背倾斜(α=70°)的临水加筋土挡墙的筋材拉力系数的影响较墙背垂直的挡墙更加显著；地震惯性力对线性布筋的临水加筋土挡墙的筋材拉力的影响较均匀分布更加显著。

图4 水位高度对KT的影响Fig.4 Influence of water level on KT

4.2 超静孔压与竖向有效应力的比值

超静孔压与地震作用时的循环震动有关，是临水加筋土挡墙地震稳定性的重要影响因素。取ru=0.3，0.7，超静孔压对筋材拉力的影响如图5所示。在相同墙背倾角、相同布筋模式和相同地震力作用下，超静孔压对筋材拉力有增大作用。如在kh=0.1时,从ru=0.3到ru=0.7，墙背倾斜的挡墙(α=70°)在线性布筋和均匀布筋下相对应的筋材拉力系数KT分别增长24.92%，24.83%；垂直挡墙KT增长24.81%，24.63%。此外，ru=0.3时，从kh=0.05到kh=0.2，在线性布筋和均匀布筋下相对应的墙背倾斜的挡墙(α=70°)的筋材拉力系数KT分别增长53.19%，44.38%，垂直挡墙的筋材拉力系数KT分别增长52.92%，43.49%；ru=0.7时，从kh=0.05到kh=0.2，在线性布筋和均匀布筋下相对应的墙背倾斜的挡墙(α=70°)的筋材拉力系数KT分别增长33.49%，25.63%，垂直挡墙的筋材拉力系数KT分别增长32.77%，24.46%。在其他条件相同的情况下,超静孔压较小时，地震惯性力对筋材拉力的影响更加显著；地震惯性力对线性布筋的临水加筋土挡墙的筋材拉力的影响较均匀分布更加显著。

图5 超静孔压对KT的影响Fig.5 Influence of excess pore pressure on KT

4.3 填土内摩擦角

图6 填土内摩擦角对的影响Fig.6 Influence of internal friction angle of filler on KT

墙土内摩擦角反映了填土抗剪破坏的极限能力，φ值是由于土粒之间的滑动摩擦以及凹凸面间的镶嵌作用产生的摩阻力的摩擦角，墙土内摩擦角是工程设计中需要考虑到的重要参数。取φ=30°，40°，填土内摩擦角对筋材拉力的影响如图6所示。在相同墙背倾角、相同布筋模式和相同地震力作用下，填土内摩擦角对筋材拉力有减小作用。如在kh=0.1时，从φ=30°到φ=40°，墙背倾斜的挡墙在线性布筋和均匀布筋下相对应的筋材拉力系数KT约减小38.15%，39.82%；垂直挡墙KT约减小29.48%，30.73%。此外，在kh=0.05时，线性布筋模式下墙背倾斜的挡墙(α=70°)的筋材拉力在φ=30°，40°时分别比均匀布筋大15.74%，12.23%；线性布筋模式下垂直挡墙的筋材拉力在φ=30°，40°时分别比均匀布筋大7.18%，5.04%。在kh=0.2时，线性布筋模式下墙背倾斜的挡墙(α=70°)的筋材拉力在φ=30°，40°时分别比均匀布筋大8.34%，8.46%；线性布筋模式下垂直挡墙的筋材拉力在φ=30°，40°时分别比均匀布筋大0.91%，1.83%。在地震惯性力系数较大时，线性布筋模式下的挡墙筋材拉力系数与均匀布筋相近，且墙背垂直的挡墙较墙背倾斜的挡墙(α=70°)更加明显。

5 结论

本研究假定滑裂面的型式为对数螺旋线，基于拟静力方法建立极限平衡方程，通过合理地选择遗传算法控制参数和设置搜索范围，有效地计算得出地震作用下临水加筋土挡墙内部稳定设计所需的筋材拉力系数。根据结果对比和参数分析得出以下结论：

(1)通过计算对比分析验证了本研究方法的可行性，表明了填土侧静水压力对临水加筋土挡墙筋材拉力系数计算的重要性。

(2)水位高度、超静孔压的增大对筋材拉力有增大作用，填土内摩擦角的增大对筋材拉力有减小作用，且这些参数对墙背倾斜的挡墙(α=70°)的影响较墙背垂直的挡墙(α=90°)更加明显；筋材拉力系数随着地震惯性力的增大而增大，且在水位高度较大、超静孔压较小时其增大幅度更加显著。

(3)在水位高度、墙背倾斜角度、填土性质、超静孔压、地震荷载等条件相同时，临水加筋土挡墙在线性布筋模式下的筋材拉力系数比均匀布筋模式小，即在相同的工况下，均匀布筋模式的临水加筋土挡墙较线性布筋而言存在一定的设计冗余。该结论对工程应用中的布筋方式有一定的参考价值。

(4)在水位高度、布筋模式、填土性质、超静孔压、地震荷载等条件相同时，墙背倾斜的临水加筋土挡墙的筋材拉力系数比墙背垂直的临水加筋土挡墙小。在工程应用中，在场地许可条件下，合理地将临水加筋土挡墙墙背设计为倾斜状可提升设计的经济性。