自适应粒子群算法在成桥索力优化中的应用
蔡 儆,张宇航,王林柯,杨雅勋,高宏伟
(1.陕西科技大学,陕西 西安 710021;2.长安大学 公路学院,陕西 西安 710064;3.西安市轨道交通集团有限公司,陕西 西安 710016)
0 引言
随着中国公路建设的发展,系杆拱桥以其较大的整体刚度、较好的力学性能、便捷的施工方法、较低的造价等特点被国内外广泛应用。系杆拱桥是一种基于拱肋、吊杆、系杆的三元结构,其外部静定内部超静定,系杆拱桥的设计过程是以合理成桥状态为目标,即在恒载作用下系杆、拱肋受力合理、主桥线形平顺。在拱桥结构已经确定的情况下,通过改变吊杆的索力可以显著影响结构受力。因此为了使结构达到目标状态就需要吊杆具有合适的成桥索力,系杆拱桥的优化问题便转化成吊杆索力的优化问题。
戴杰[1]等人对当下斜拉桥索力求解方法进行了综述,主要方法有:指定结构状态的优化方法、数学优化法、分布优化法等。而目前系杆拱桥吊杆的索力求解方法主要是沿用了一些斜拉桥的索力求解方法,Leonhardt率先提出了刚性支撑连续梁法并最早应用于美国P-K桥的分析中;肖汝城[2-3]结合影响矩阵推导了弯矩最小能量法的公式;梁鹏[4]提出通过调整结构刚度来近似的求解最小弯曲能量法。传统的调索方法因受限于各自的局限性而不具有普遍适用性,如刚性支撑连续梁法不能考虑多条件的约束问题,因而用其计算的索力值往往不合理;弯曲最小能量法在结合影响矩阵情况下,想要精确求解计算会十分繁琐,而采用近似求解方法也需要不断调节结构的刚度才能使其达到预期结果。
为了避免传统调索方法的缺点,且能够快速有效的求解出索力,出现了将计算机智能优化算法与数学方法相结合的调索方法,Ha[5]等人提出微遗传算法并对斜拉桥成桥索力进行了优化,陈志军[6]、吴霄[7]等人分别采用传统的粒子群和遗传算法对斜拉桥索力进行了优化,但传统的智能优化算法因其自身的局限性导致结果往往不够理想。为了使结果更加准确,本研究以实际工程项目为依托,通过对粒子群优化算法加以改进并与影响矩阵相结合,在同时兼顾计算效率和多目标约束的条件下求解吊杆索力,并与其他多种方法进行分析比较,从而验证该方法的可行性。
1 基于改进粒子群算法的索力优化
1.1 粒子群算法原理
粒子群算法最早是由Kennedy和Eberhart[8]提出的一种基于群鸟觅食的仿生智能算法。其原理是群鸟在觅食的过程中,每只鸟的初始位置和飞行方向都处于随机的状态,而且不知道最佳的觅食点在何处。鸟群间通过相互学习、信息共享,并在每次觅食过程中结合自身经验和种群之间的信息传递不断调整速度和位置,最终步步逼近食物,示意图如图1所示。
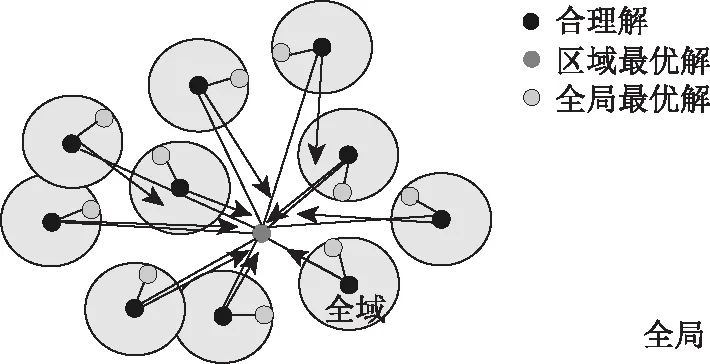
图1 粒子寻优示意图Fig.1 Schematic diagram of particle optimization
如果将该方法运用到实际应用中,则是把鸟群抽象为m个没有质量和体积的粒子,再将其延伸至N维空间,粒子在N维空间中的位置表示为Xi=(xi1,xi2,…,xij),速度表示为Vi=(vi1,vi2,…,vij),且其位置和速度需限制在[Xmin,Xmax]和[Vmin,Vmax]范围内。每个粒子都有一个由目标函数决定的适应度值fitness,并且知道自己迄今为止发现的最好位置pb=(pi1,pi2,…,pij)和群体发现的最好位置gb=(g1,g2,…,gj)。粒子通过追踪pb和gb来更新自己的速度和位置,且速度和位置更新公式为:
(1)
(2)
式中,i为粒子的个数,i=1,2,…,m;j为例子的维度,j=1,2,…,N;k为迭代步数;w是惯性因子;c1,c2为学习因子;r1,r2为[0,1]范围内的均匀随机数;vmax为用户自定义常数,一般取vmax=aXmax,vmin=aXmin,通常a为0.1~0.2。
1.2 调索目标函数
目标函数下每一个粒子都有一个适应度值,它作为每次迭代的临时储存变量,并不具有记忆性,优化算法可通过粒子每次迭代的适应度值来评价结果的好坏,进而不断地寻优最终靠近目标。实践证明[9-10],通过限制拱桥结构的弯曲能量所求解的吊杆索力能使桥梁结构处于一个较好的受力状态,然而拱桥在受弯的同时也受压,因此本研究以系杆拱桥的系梁弯曲应变能和拱肋压缩应变能之和为目标,并将结构离散化,离散后的应变能公式为:
(3)
式中,U为结构的应变能之和;m为离散单元的数量;Li,Ai,Ei,Ii,Mi,Ni分别为单元的长度、面积、材料的弹性模量、截面惯性矩、弯矩和轴力。
为了能够建立起设计变量(拱桥的吊杆索力)与优化目标间的函数关系,可采用影响矩阵原理作为连接二者的桥梁,进而达到索力优化的目的。影响矩阵公式具体表示为:
AY=D,
(4)
式中,Y为施调向量,在本研究中是指吊杆索力组成的列向量;D为受调向量,是指结构中关心截面上若干独立元素所组成的列向量。这些元素一般是指关心截面的内力、位移,通过将这些元素调整到期望状态来求解施调向量Y。A为影响矩阵,是指当施调向量的某一向量发生单位变化时,引起受调向量D的变化量。
从式(3)可以看出,当结构确定时,其单元及材料的具体特性已经确定,因而只能通过改变截面弯矩和轴力来调整应变能的大小。因此不妨令受调向量为截面的弯矩和轴力,且调索前弯矩向量为M0、轴力向量为N0,施调向量X=[S1,S2,…Sn]T,其中S为吊杆索力,则调索后的弯矩M和轴力N为:
(5)
将式(5)代入式(3)可得结构的目标函数为:
U=M0TBM0+M0TBC1X+
XTC1TBM0+XTC1TBC1X+
N0TQN0+N0TQC2X+XT
C2TQN0+XTC2TQC2X,
(6)
式中,矩阵B和Q均为系数矩阵,是对角阵,分别表示单元柔度对单元弯矩和轴力的加权矩阵,bii=li/2EiIi、qii=li/2EiAi,C1、C2分别表示单位索力引起弯矩和轴力变化的影响矩阵。
1.3 索力约束条件
对于系杆拱桥,其系梁主要承受弯矩,拱肋受轴力作用,因此就必需对其弯矩、轴力加以约束以使其落在允许的范围内。弯矩的约束条件可表示为Mmin≤M≤Mmax,轴力的约束条件可表示为Nmin≤N≤Nmax。根据影响矩阵理论,在对弯矩、轴力进行限制的同时也相当于对索力进行了约束,从而使调索后的最优解具有了合理性。即当Mmin≤M≤Mmax、Nmin≤N≤Nmax时,可得索力约束条件为:
式中,Si为第i根吊杆的索力;Mjmax,Mjmin分别为系梁上第j个单元所允许的最大、最小弯矩;M0j为系梁第j个单元初始弯矩;Njmax,Njmin分别为拱肋上第j个单元所允许的最大、最小轴力;N0j为拱肋第j个单元初始轴力。同时为了满足索力均匀原则,需将相邻索力的差值限定在可控范围内,另对索力做以下约束:
(9)
式中Δ为索力均匀度的评价阈值。
1.4 粒子群算法改进
由于传统粒子群算法的程序实现过程十分简洁,且需要调整的参数较少,因此在随机优化算法中具有强劲的优势,并被广泛应用于工程领域。但同时它也存在收敛速度慢、局部搜索能力差等缺点。为了提高算法的适应范围,使其结果更加准确可靠,为此我们需要对传统的算法进行改进[11-13]。研究结果表明[14-18],当w较大时,算法的全局搜素能力较强,w较小时算法的局部搜索能力较强,因此算法的优化问题便可转化成一个w值的选取问题,即当粒子目标值趋于局部最优时,需要增大惯性因子;当粒子目标值比较分散时,则需减小惯性因子。
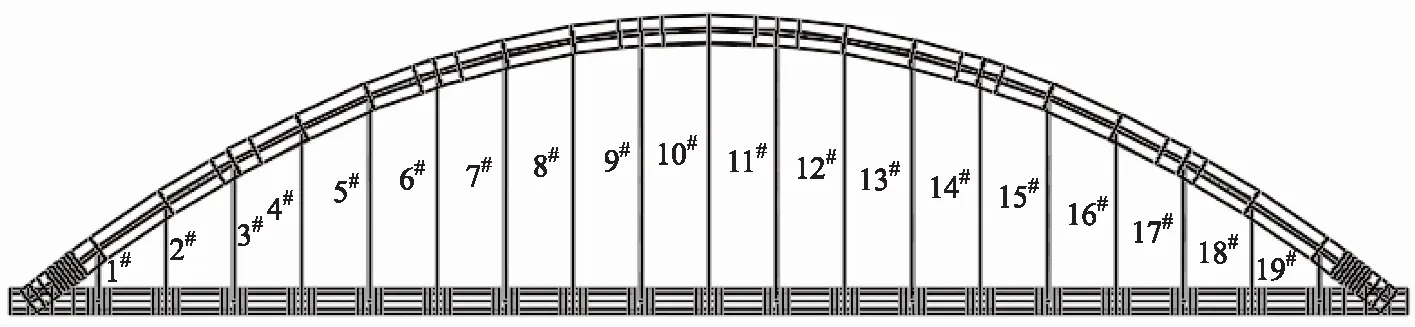
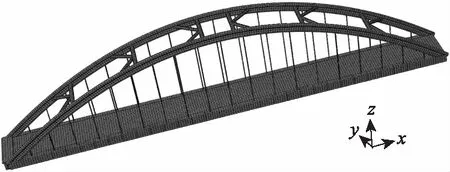
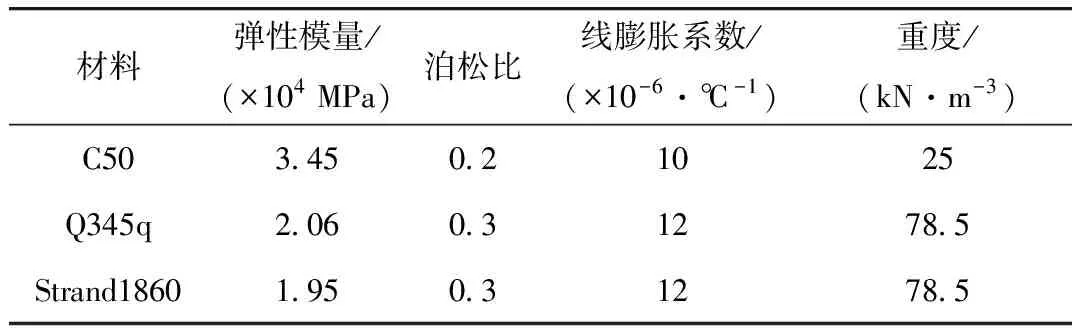
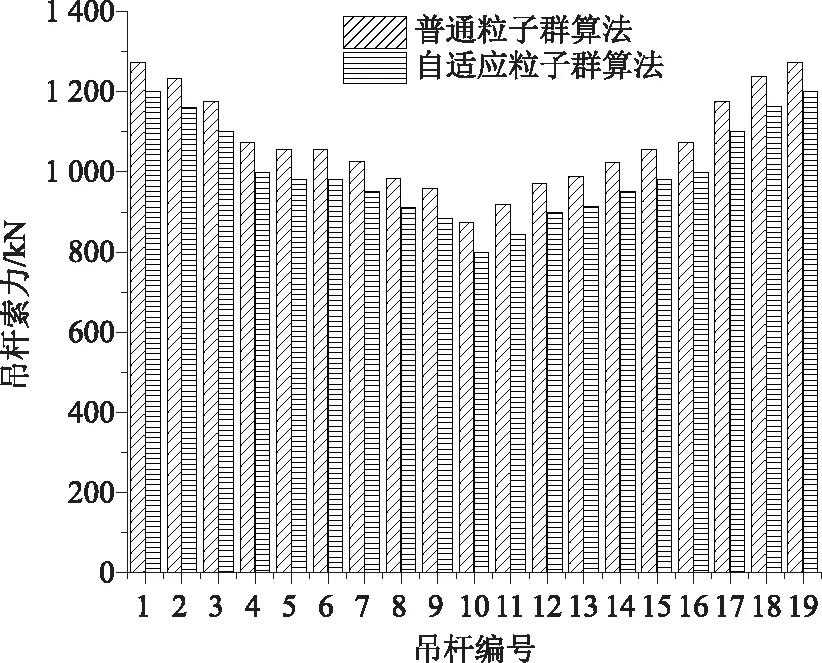
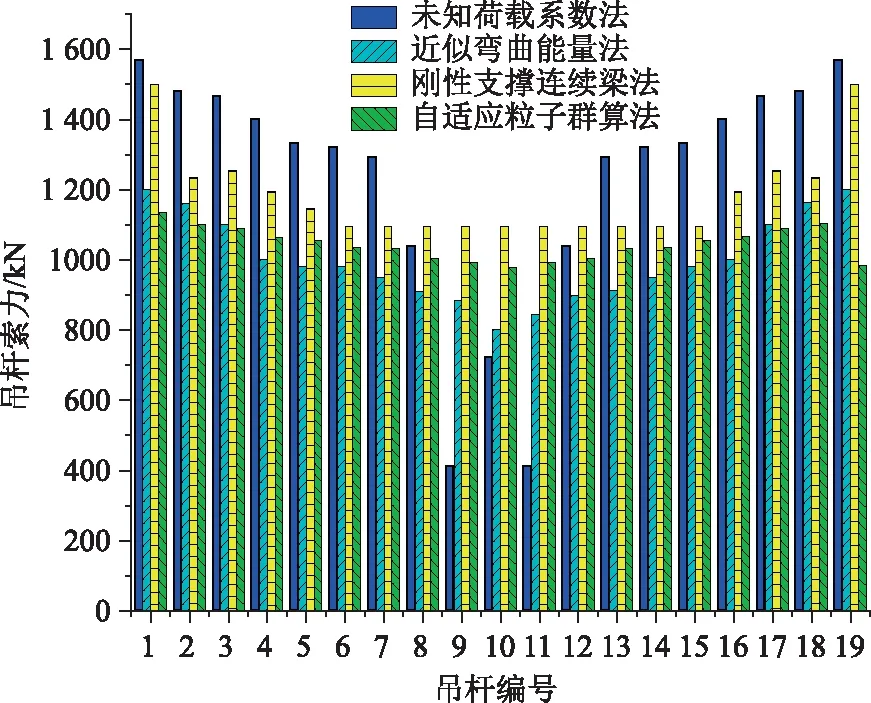
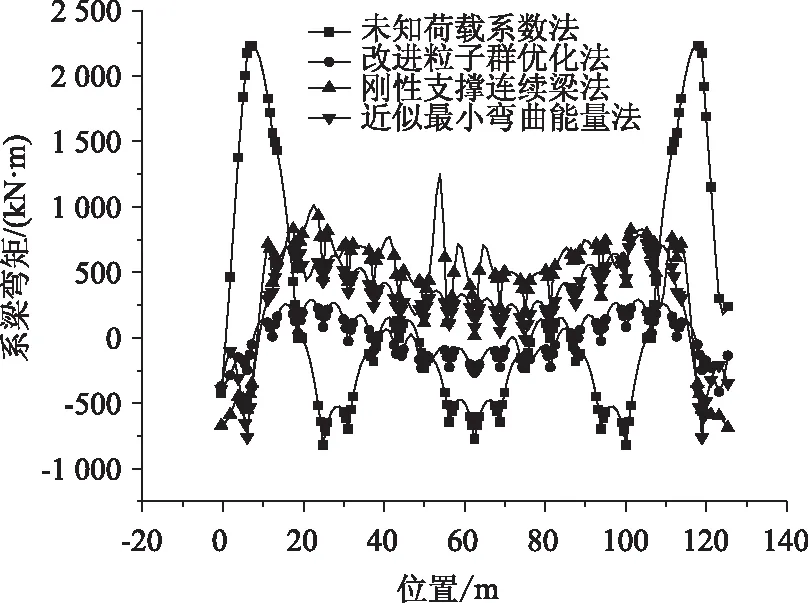
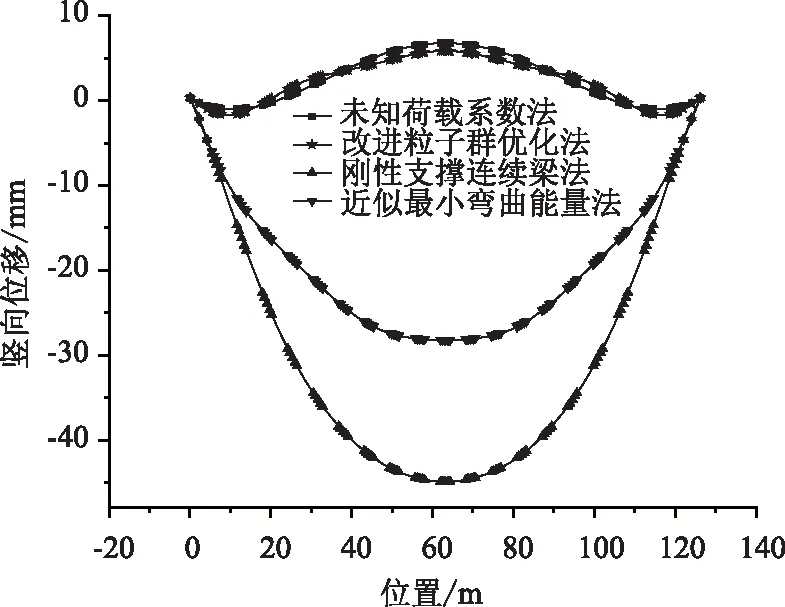
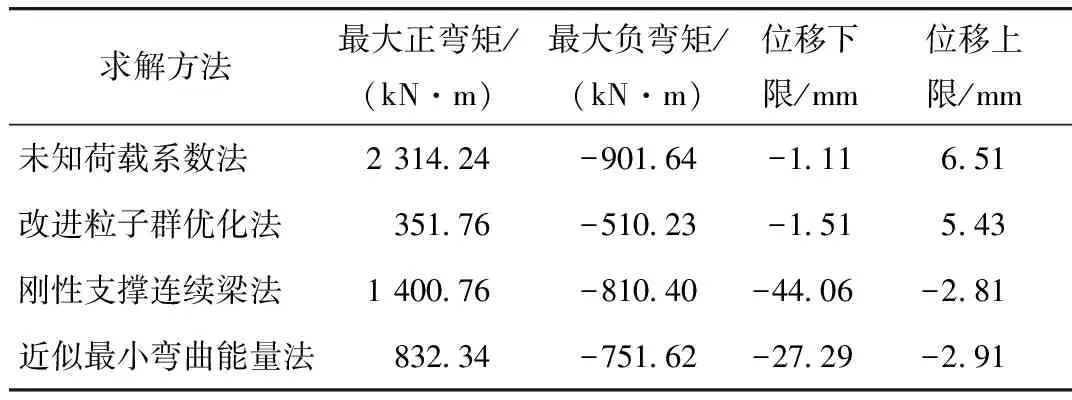
为了合理选取w,本研究将权重进行自适应调整,通过判断粒子当前的目标函数值U的好坏来自动调整w,即当U>Uavg,此时粒子的目标函数值要比平均目标值差,为了使其向较好的搜索区靠拢,对应的惯性因子要较大;当U′avg (10) 式中,wmax,wmin分别为w的最大和最小值;Umin,Uavg分别表示当前所有粒子的最小适应值和平均适应值。由于本研究是以弯曲能量的最小值为目标,因此U′avg是将所有小于Uavg的适应值取平均所得。 本研究将索力调整和计算机智能优化算法结合,并考虑了惯性权重的实时变化,使索力调整过程自动化,从而实现索力的高效寻优。其具体步骤如下: (1)利用有限元软件建立拱桥模型,并提取相关结构数据及影响矩阵作为基础数据库。 (2)建立目标函数,利用Matlab软件编程粒子群算法并搜索在约束范围内的最优解,如果满足停止条件,则输出当前解,否则更新权重继续搜索。 (3)将搜索值回代有限元模型,校核结果的有效性。 本研究优化后的调索路线具体计算流程如图2所示。 图2 计算流程图Fig.2 Flowchart of calculation 本研究以某刚性系杆刚性拱桥位工程实例,主桥总长160 m,计算跨径156.28 m,桥梁总宽13.9 m,拱轴线为二次抛物线,矢跨比为1/5。拱肋采用哑铃型钢管混凝土,采用Q345q钢材,内充C50微膨胀混凝土。系梁采用箱形断面,系梁和横梁为预应力混凝土结构,桥面2%横坡通过横梁高度的变化进行调整,吊杆间距为7.8 m,每片拱肋设吊杆19根,吊杆编号由小里程到大里程依次为1#~19#,如图3所示。 图3 吊杆编号示意图Fig.3 Schematic diagram of suspender numbering 本研究系杆拱桥采用有限元软件Abaqus建模,如图4所示。除吊杆采用桁架单元外,其余均采用梁单元。恒载作用下主梁的初始弯矩值M0和拱肋轴力值N0通过软件的数据提取功能来提取。通过分别改变每根吊杆的初拉力,使其发生单位1的变化,得到关键节点的弯矩和轴力变化值从而组成影响矩阵。模型的主要材料特性见表1。 图4 系杆拱有限元模型Fig.4 Finite element model of tied arch 表1 材料特性Tab.1 Material properties 利用Matlab工具编写改进前和改进后的粒子群算法程序并进行迭代求解,改进前后除惯性权重外,其他系数取值相同。目前w较典型的取值范围是0.4~0.9,算法在此范围内取值能获得较好的局部和全局收敛性能。由1.4可知,为使算法能在初期计算时找到较好的解,需要取较大的惯性权重值,因此本研究对改进前的惯性权重w恒取0.9,改进后惯性权重系数按式(9)计算,学习因子取c1、c2取Bergh F[19]的推荐值并精确至小数点后两位,种群规模m取50,索力范围取[500,1 500],速度范围取索力范围的15%,具体数据见表2。由图5、图6可以看出,在迭代次数都为300次的条件下,改进后的算法收敛速度得到明显提高,在收敛精度方面也有一定的改善。 表2 改进后粒子群算法参数Tab.2 Improved PSO parameters 图5 算法改进前后效果对比Fig.5 Comparison of effects before and after algorithm improvement 图6 算法改进前后索力对比Fig.6 Comparison of cable forces before and after algorithm improvement 图7 索力对比Fig.7 Comparison of cable forces 如何控制拱桥的内力和线形使其在安全的范围内是施工监控过程中的重要环节。为了能够清楚地展示粒子群优化算法在实际工程中的效果,本节除使用研究中提出的改进粒子群算法外,另使用近似的弯曲能量法、刚性支撑连续梁法及未知荷载系数法对索力进行求解,4种方法求得的索力见图7。从图7中可以看出,利用改进后的粒子群优化算法求得的索力值较其他3种方法更加均匀适中。 将4种方法求得的索力再分别代入有限元模型中,得到各索力下系梁弯矩和竖向位移,如图8、图9所示。从图8可以看出,用不同方法约束的系梁弯矩在数值和均匀度上都有较大的差异,其中未知荷载系数法约束的弯矩上下峰值差距较大,刚性支撑连续梁法约束的弯矩出现骤增现象,这与该方法在吊杆数量有限情况下,可能会导致结构其余部位出现状态异常有关,而本研究的改进粒子群优化法和近似最小能量法优化后的系梁弯矩都比较均匀,但本研究方法得到的结果比近似最小弯曲能量法得到的结果在数值上更小。从图9可以看出,刚性支撑连续梁法和近似最小弯曲能量法优化后的竖向位移较大,本研究的改进粒子群优化法和未知荷载系数法优化后的竖向位移相近,但本研究的改进粒子群优化法较未知荷载系数法优化后的竖向位移更加均匀。4种方法对结构具体影响见表3。 图8 系梁弯矩图Fig.8 Bending moments of tie beam 图9 竖向位移Fig.9 Vertical displacements 表3 四种优化方法对结构的影响Tab.3 Influence of 4 optimization methods on structure 本研究在粒子群优化算法的基础上对其惯性权重进行改进,同时考虑了系杆拱桥在索力优化过程中的主要约束条件,提出了一种新的系杆拱桥索力优化的方法,并以某系杆拱桥为工程背景进行应用,主要结论如下: (1)基于粒子群算法的调索方法可以借助有限元软件和数值分析软件实现索力的自动化、智能化求解。在改进后算法的寻优能力得到提高,从而避免了繁琐的试算过程,进而可以高效、准确地求解出索力,极大提高了调索效率。 (2)粒子群算法改进后较改进前在收敛速度和精度上有一定的改善。 (3)4种索力优化方法的结果表明,改进后的粒子群算法较其他3种方法能更加全面地考虑影响因素的作用,进而规避不利因素对优化结果的影响,以达到更好的优化效果。 (4)本研究提出的方法可进一步推广于各施工阶段过程中吊杆初拉力的确定问题。1.5 调索路线优化
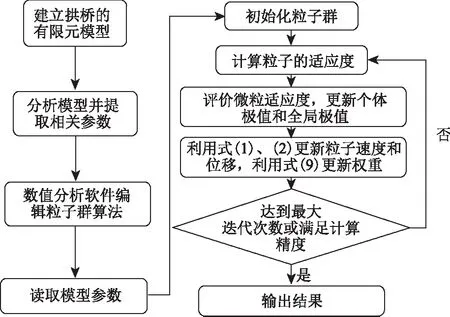
2 工程应用
2.1 工程实例
2.2 参数设置

2.3 优化结果分析
3 结论

