基于改进的AHP-SPA的边坡稳定性评价及工程应用
李志强,徐 斌,王 升,文 桃
(1. 潍坊学院 建筑工程学院, 山东 潍坊 261061; 2. 山东高速集团有限公司潍坊分公司, 山东 潍坊 261100;3. 长江师范学院 土木建筑工程学院, 重庆 408100; 4. 山东大学 岩土与结构工程研究中心, 山东 济南 250061)
0 引言
我国是世界上自然灾害最严重的国家之一,如滑坡、泥石流等。在降雨极为丰沛的西南山区,滑坡灾害频繁发生,严重威胁着公路、铁路、航运等交通安全及附近居民的生命财产安全。因此,边坡的稳定性分析一直是岩土工程领域的研究热点,也是难点。
针对边坡的稳定性问题,国内外学者开展了大量的研究。Kirschbaum[1]通过耦合区域滑坡敏感地质图与卫星降雨估计值,来进行滑坡灾害的态势感知,并成功应用于中美洲和加勒比群岛地区。Teoman[2]和Ahmad[3]等人分别采用极限平衡法、赤平投影法研究了公路边坡的稳定性分析。我国早期研究主要集中在基于土力学极限平衡分析法,但这些方法未能充分考虑边坡的水文地质条件。为此,考虑多影响因素的边坡稳定性评价方法逐渐成为研究热点,如模糊理论[4,6]、神经网络[7]、TOPSIS法[8]、属性模型[9-10]、可拓理论[11-13]、遗传算法[14]等。但是,滑坡灾害是一个受多因素影响且具有时空变异性的复杂动力现象,具有随机性和模糊性。针对上述问题,本研究引入集对分析法解决这一确定和非确定共存的边坡稳定性问题。在充分考虑水文地质因素与外部诱发因素的基础上,建立了边坡AHP-ISPA稳定性评价模型,为预测滑坡灾害风险提供了一种有效的方法。
1 公路边坡稳定性评价方法
1.1 评价指标体系
边坡工程稳定性评价对象是坡体,赋存介质是具有非连续性、各向异性的岩土体,同时又受到外部的自然因素和工程因素影响。高陡边坡作为一个开放的多场耦合系统,影响其稳定性的因素是极其复杂多样的[8,15]。然而,选取科学、合理的评价指标体系是进行边坡稳定性综合评价的关键,指标太多不仅会削弱主控因素还会造成计算量过大,指标过少会影响评价结果的可靠性[14-15]。为此,本研究统计分析了汶川地震诱发的巨型滑坡——大光包滑坡、黑方台滑坡、秭归千将坪滑坡、万州吉安滑坡等近百余例典型滑坡的诱发因素,并借鉴国内外学者的研究成果及相关规范[9,16],从坡体形态、岩土体特征、水文状况、自然诱因4个方面选取了13个二级指标,建立了高边坡稳定性评价多层次评价指标体系[17],如图1所示。

图1 边坡稳定性多层次评价指标体系Fig.1 Slope stability multi-hierarchy evaluation indicator system
1.2 评价等级及分级标准
根据边坡的稳定程度,结合滑坡灾变演化全过程,将其划分为稳定(Ⅰ)、较稳定(Ⅱ)、不稳定(Ⅲ)、极不稳定(Ⅳ),描述见表1。然后确定各评价指标的分级标准与临界阈值,见表2。

表1 边坡稳定性分级标准Tab.1 Classification criterion of slope stability
1.3 集对分析理论与方法
集对分析理论(SPA)是由赵克勤教授提出的一种用于处理确定不确定问题的系统分析方法,其核心思想是将多维复杂的目标问题视为一个确定-不确定系统,用“同一”和“对立”描述确定性,用“差异”描述不确定性,从同、反、异3方面分析研究系统中各元素间相互联系、相互制约,却又相互转化的复杂关系[17-19]。
1.3.1 传统集对分析理论
在给定集合A、B,两个集合形成集对H(A,B),则集对H(A,B)的联系度可表示为:
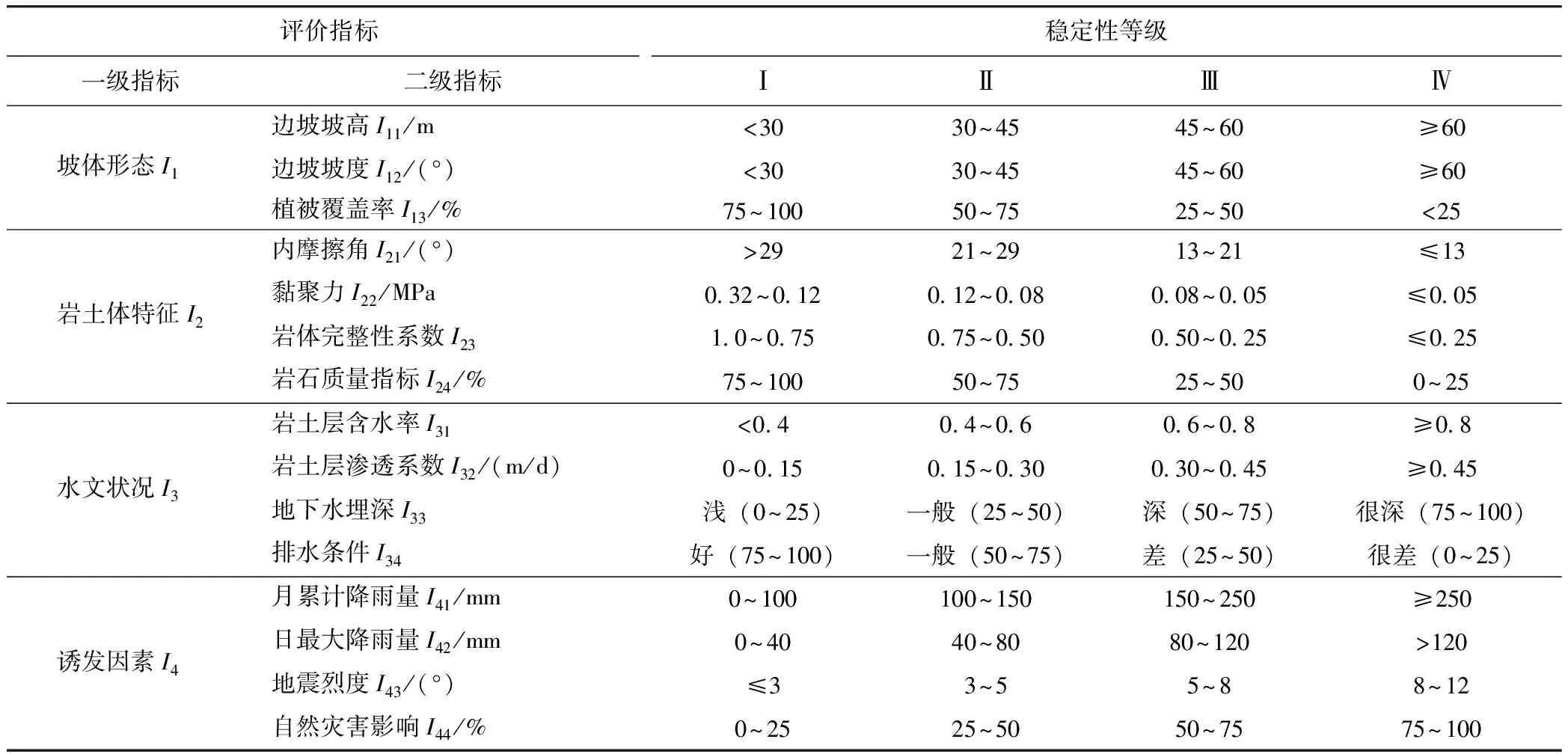
表2 评价指标等级划分标准Tab.2 Classification criterion of evaluation indicator grades
(1)
式中,μA-B为联系度;N为集对H(A,B)的所有元素数量;S为集合A、B所共同的元素数量;P为集合A、B相互对立的元素数量;F=N-S-P,是集合A、B既不相互对立、也不相互具有的元素数量;S/N=a,代表同一度;F/N=b,代表差异度;P/N=c,代表对立度,满足a+b+c=1;i为差异度系数,i∈[-1,1];j为对立度系数,j=-1;i和j也可仅作为标记作用。
1.3.2 改进集对分析理论(ISPA)
通过对传统集对分析理论进行研究,发现其存在以下缺陷:
(1) 传统集对分析理论只是将系统分为同一、对立、差异3个类型,而边坡工程是一个具有多维度不确定性的复杂动力系统,简单的同反异关联关系无法全面、准确地描述影响因素与风险等级之间的相互作用规律。
(2) 根据公式(1)可知,传统理论中同一度a、差异度b、对立度c的准确量化方法对样本数据要求较高,量多、准确且具有代表性。
针对上述问题,对集对分析理论进行了改进。首先,将同异反细化为同一、优异、劣异、优反、劣反5个类型,如图2所示。

图2 集合A、B的同异反联系示意图Fig.2 Schematic diagram of relation of identity, opposition and difference of set A and set B
假设X为评价对象集,X={X1,X2,…,XL};评价对象Xl(l=1, 2,…,L)有n个评价指标,评价指标集记为I={I1,I2,…,In}。每个评价指标Ii(i=1, 2,…,n)对应K个危险等级,评语集C={C1,C2,…,CK}。在集合I与集合C形成的集对H=(I,C)中,当ti∈Ck时,分析评价指标Ii与危险等级Ck(k=1, 2,…,K)的关系:
① 认为与等级Ck同一,令同一度a=1;
② 对于风险相对较低的相邻等级Ck-1,认为优异,差异度记为b1;
③ 对于风险相对较高的相邻等级Ck+1,认为劣异,差异度记为b2;
④ 对于风险较低的相隔等级Ck-2,则认为是优反,对立度记为c1;
⑤ 对于风险较高的相隔等级Ck+2,则认为是劣反,对立度记为c2。
同时,将式(1)改写为:
μ=a+(b1+b2)i+(c1+c2)j=a+b1i++b2i-+
c1j++c2j-,
(2)
式中,a+b1+b2+c1+c2=1。
引入模糊数学理论确定参数a,b1,b2,c1,c2,则待评指标对应4个风险等级的联系度函数如下:
(3)
(4)
(5)
(6)
将评价指标的实际测量值代入式(3)~(6),可得到评价指标集与风险等级集的联系度矩阵U,记U=[μij]n×K。在此基础上考虑各评价指标权重来计算综合联系度矩阵D:
(7)
式中,W为权重向量;wi为评价指标Ii的权重。
1.4 基于FAHP的权重确定方法
对于边坡稳定性问题,不同因素对滑坡灾害的影响程度是不一样的,引入权重来表征评价指标对滑坡风险的重要程度。当某一指标较重要时,其权重值越大;反之,权重值越小。因此,所确定权重的合理性直接影响着评价结果。为准确刻画评价指标的权重值,本研究提出了基于三角模糊数理论(TFN)与层次分析法(AHP)相结合的赋权方法。
(1)TFN-AHP
层次分析法是美国学者提出的,采用1~9标度法(见表3)构造一个n阶判断矩阵M=(mij)n×n;其中,n为评价指标数量,mij表示评价指标Ii和Ij之间的相对重要程度。然而,滑坡灾变是多因素共同作用下的复杂过程,因素之间的相关关系具有模糊性。仅凭某一确定的标度值来衡量因素间的相对重要程度,容易造成有效信息的丢失。为此,引入三角模糊数理论对层次分析法进行改进。

表3 Saaty等建议的1~9标度法Tab.3 1-9 scale method recommended by Saaty, et al
(2)具体步骤

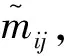
(8)
对于三角模糊数
(9)
(10)
B=(b1,b2,…,bn),
(11)
式中,B为对应判断矩阵的评价指标特征向量,bi(i=1, 2, …,n)为评价指标Ii的特征值。
③ 根据公式(12)~(13),对判断矩阵进行一致性检验。
(12)
(13)
式中,λmax为特征向量的最大特征值。CI为一致性指标;RI为平均随机一致性指标,具体取值参考文献[20]。当CI与CR均小于0.1时,判断矩阵满足一致性检验。

(14)
引入模糊直觉理论中的得分函数[21],见式(15),计算各指标的初始权重向量W′=(w′1,w′2,…,w′n):
(15)
⑤根据公式(16)进行归一化处理,最终得到权重向量W=(w1,w2,…,wn)。
(16)
式中,i,j=1, 2,…,n。
2 工程应用
自三峡蓄水以来,三峡库区滑坡灾害频繁发生,国内外学者开展了大量研究,但依然是屡禁不止。究其原因是库区水位升降,降水丰富,地势起伏多变,地质条件复杂,且地质构造活跃等。本研究以位于三峡库区的重庆市巫山县大宁河江东寺岸坡为例,验证改进AHP-SPA模型的实用性与合理性,同时为三峡库区滑坡灾害的超前预警提供依据。
巫山县是长江中上游“黄金水道”的重要水路交通枢纽,大宁河江东寺岸坡属于中-浅褶皱侵蚀、剥蚀低山地貌,地势总体呈北东高南西低,坡度30°~40°,坡高130~350 m。大宁河在岸坡西南侧从北向南汇入长江,当前水位高程为143.31 m,区内与水平面的最大高差为346.79 m。岸坡区内地层从上到下依次为人工填土、残坡积土层、灰岩,如表4所示。位于巫山向斜南翼的一个次级背斜近核部,岩层产状为320°~347°∠27°~40°,结构面较平整,裂隙呈张开状,宽度为1~8 mm。此外,区域降雨丰沛,具有明显的季节性,主要集中在5~9月份。根据地质勘察资料和试验数据[9,21],得到评价指标实测值,见表5。
2.1 权重确定
采用Saaty等建议的1~9标度法,构造各二级评价指标的判断互补矩阵,根据公式(4)~(8)计算二级评价指标的权重,详见表6。然后构造一级评价指标的判断互补矩阵,计算一级评价指标的权重。

表4 江东寺岸坡岩土层特征Tab.4 Lithologic features of Jiangdongsi bank slope

表5 评价指标实测值Tab.5 Measured values of evaluation indicators

表6 评价指标权重判断矩阵Tab.6 Judgement matrix of evaluation indicator weights
(17)
2.2 计算同异反联系度
将表4中的评价指标实测值,代入表2中的联系度函数,计算二级评价指标的联系度,见表7。首先将其与二级指标权重耦合,计算一级评价指标联系度矩阵,再与一级指标权重进行相乘,最终得到综合联系度矩阵,见式(9)。
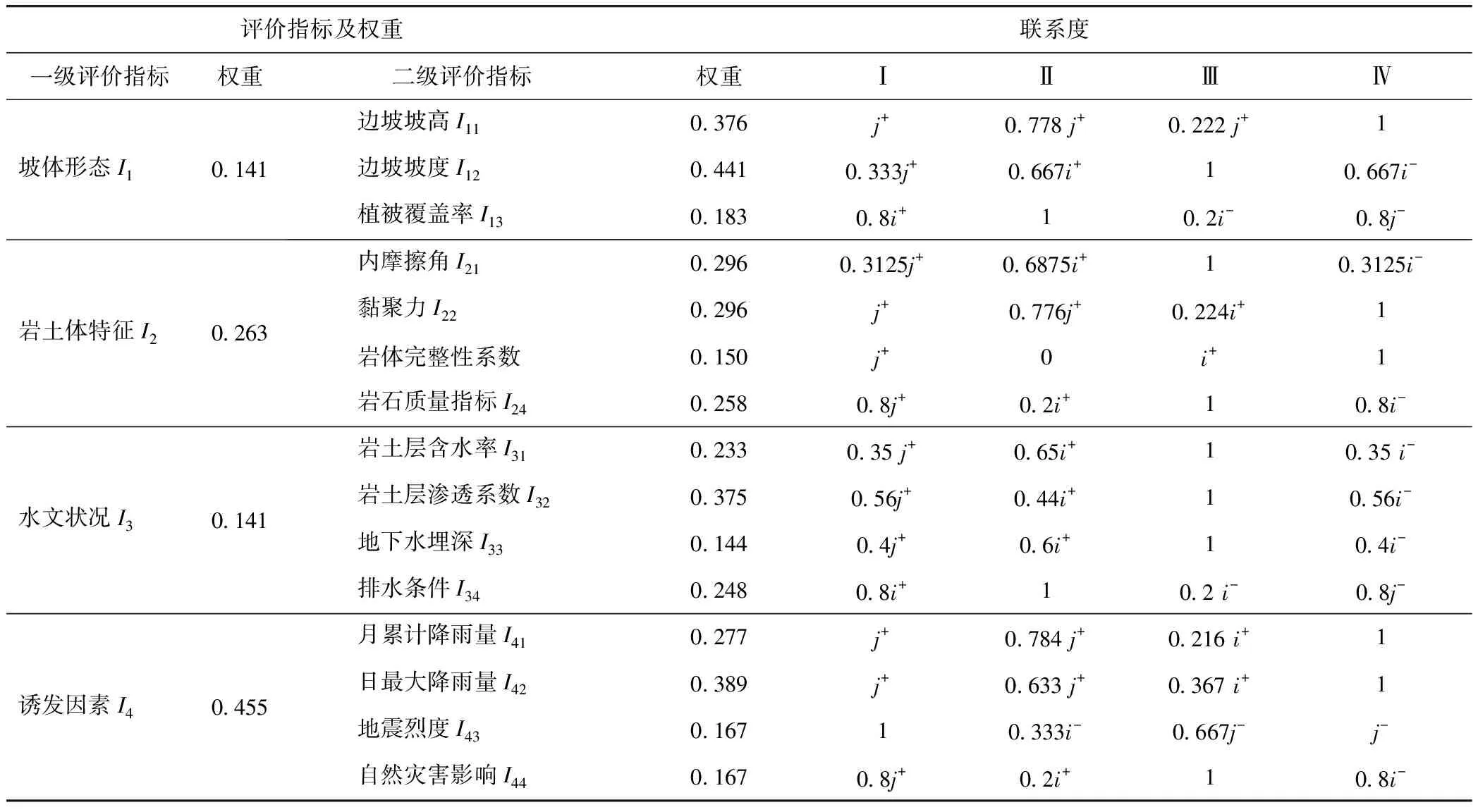
表7 基于本方法所计算的联系度Tab.7 Connection degrees calculated by proposed method
D=(0.156, 0.343, 0.261, 0.239)·
(0.04+0.074i++0.634j+, 0.093+0.238i++0.013i-+0.157j+, 0.395+0.123i++0.019i-+0.013j++0.027j-
0.471+0.286i-+0.114j-)。
(18)
2.3 灾情验证
由于i+,j+,i-,j-∈(0,1),且满足i+>i->0,j- (1)通过对百余例典型滑坡灾害影响因素的调查与分析,从坡体形态、岩土体特征、水文状况、诱发因素4个方面选取了坡高、坡度、岩体完整性、黏聚力、内摩擦角、岩土层含水率、日最大降雨量等15个评价指标,建立了科学的边坡多层次稳定性评价指标体系,同时提出了评价指标的风险等级划分标准。 (2)边坡作为一个多场耦合作用的复杂动力系统,其失稳具有随机性与模糊性。为此,将集对分析理论引入边坡稳定性评价。针对传统的集对分析将系统简单地划分了同、异、反3个类型,本研究进一步细化为同一、优异、劣异、优反、劣反5个类型,并提出了评价指标与危险等级之间的关联度函数;基于三角模糊数与层次分析法建立了评价指标的赋权方法。 (3)本研究以重庆市巫山县大宁河江东寺岸坡为背景,通过现场勘察量化了各评价指标的实际值,基于改进的AHP-SPA评价模型确定了江东寺岸坡危险等级为Ⅳ(极不稳定),评价结果与实际情况相一致,验证本方法的科学性与实用性。3 结论

