局部静荷载作用下加筋对土拱效应的影响

李格烨，徐 超，沈盼盼，张兴亚，罗敏敏，梁 程

（1.同济大学土木工程学院，上海 200092；2.中国长江三峡集团有限公司上海勘测设计研究院有限公司，上海 200434；3.新城商业管理集团有限公司上海分公司，上海 200000；4.浙江大学建筑设计研究院有限公司，浙江杭州 310027；5.中国长江三峡集团有限公司科学技术研究院，北京 100038）

土拱效应的本质是活动土体与其相邻的稳定土体间由于相对位移而产生的应力传递［1］，是岩土工程中常见的现象。例如，由于地裂缝、岩溶等地质灾害的存在，土体中易出现局部空洞，引发了空洞上覆土体的土拱效应。土拱的稳定性对上覆土体的稳定性影响巨大，决定了相关工程的安全性。此外，在垃圾填埋场复合衬垫系统下卧土体中可能发生局部沉陷或空洞，导致衬垫系统破坏，引发不必要的环境污染，甚至整体失稳［2］。因此，研究局部空洞引起的土拱效应对于实际相关工程的设计有着重要的现实意义。

针对空洞引起的土拱效应，关于填料自重和均布超载作用下的研究众多［1，3-5］，并形成了相应的计算理论。然而，土拱在局部荷载作用下可能会发生退化甚至破坏。针对该问题，Al-Naddaf等［6］通过平面应变的活动门试验研究了局部荷载作用下的土拱退化机制。Xu等［7］研究了局部静动荷载下的土拱变形和力学特性。结果表明，荷载幅值越大、频率越高、作用面积越小，其对土拱的削弱作用越明显。Zhang等［8-9］利用透明土技术开展平面应变的活动门试验，结果表明，多拱相互作用、填料高度较低和较高频率的动荷载均会加速土拱的退化甚至破坏，并引起较大的表面位移。

近年来，筋材在防止土拱退化方面的作用逐步被认识。如：Al-Naddaf等［6］的研究表明筋材的存在有助于增强土拱的稳定性。Aqoub等［10］开展了桩承式加筋路堤的模型试验，发现筋材提高了荷载传递效率，并减小了路堤的表面沉降。但是，针对局部荷载作用下筋材性质（如筋材极限拉伸强度和拉伸刚度）对土拱效应影响，目前的研究较少；此外，目前的研究多集中于一层加筋；而在实际工程中，两层甚至多层筋材的使用较为普遍。因此，有必要进一步研究局部荷载作用下加筋对土拱的影响。

本文通过平面应变活动门试验装置，设置了4种筋材布置方式，开展了填料自重和局部静荷载作用下的活动门试验，分析了局部荷载作用下筋材受力和土拱率的变化规律，并提出了预测活动门或筋材挠曲段上局部静荷载引起的竖向附加应力的理论计算方法。

1 活动门试验简介

1.1 试验装置

平面应变活动门试验装置如图1所示［7，11］，试验箱底部设有7个活动门装置（B1～B7）。如图2所示，活动门装置（B1～B7）由木块、力传感器、升降电机和位移传感器组成。中间的活动门宽度B为128 mm，该活动门装置可通过控制电机实现木块单独升降，位移传感器记录木块的位移，力传感器记录木块的受力。为了避免填料与试验箱前后的摩擦，试验箱的厚度设计为51 mm，略大于木块的厚度d（50 mm）。试验箱前表面由透明的钢化玻璃组成，方便高速相机拍摄照片，可通过粒子图像测速法（particle image velocimetry，PIV）［12］获得填料及筋材变形。试验箱上部有伺服加载装置，加载板长度L=3B=384 mm。

图2 试验箱照片Fig.2 Photo of the trapdoor box

1.2 填料

相似土可消除颗粒与试验箱侧壁的摩阻力，被广泛应用于平面应变条件的试验中。因此，本研究采用2D相似土作为填料代替砂土，相似土由三种不同直径（3、4、5 mm）、长度50 mm的铝棒、按质量比1：1：1混合而成，其重度γ为22.4 kN·m-3，经双轴试验测得内摩擦角φ为25°，粘聚力c为0。此外，本研究采用的2D相似土在保证力学性质相似的前提下，粒径较砂颗粒更大，有利于PIV处理，使填料及筋材的变形测量更为精确；并且铺设过程更加方便、快捷且可重复性较好。为了确保力均匀地传递到活动门装置下方的力传感器上，在填料底部设计了由5层直径5 mm的铝棒组成的垫层，如图1、2所示。该垫层的厚度T为22.4 mm。垫层厚度T与活动门宽度B的比值是0.175。填料的高度H为256 mm，是活动门宽度B的两倍（H=2B）。

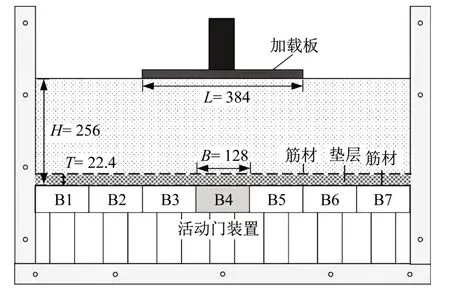
图1 活动门试验装置图（单位：mm）Fig.1 Schematic of the trapdoor test(unit:mm)

1.3 筋材

本研究中选用两种规格的牛皮纸（筋材1和筋材2）作为加筋材料。牛皮纸的刚度由拉伸试验测定，其结果如表1所示。其中，筋材1的极限抗拉强度分别为21.5 kN·m-1，2%应变所对应的筋材刚度约为1 131 kN·m-1，0.1%应变所对应的筋材刚度约为876 kN·m-1；筋材2的极限抗拉强度约为46.5 kN·m-1，2%应变所对应的筋材刚度约为2 236 kN·m-1，0.1%应变所对应的筋材刚度约为1 562 kN·m-1。因此，筋材2的刚度约为筋材1的2倍。

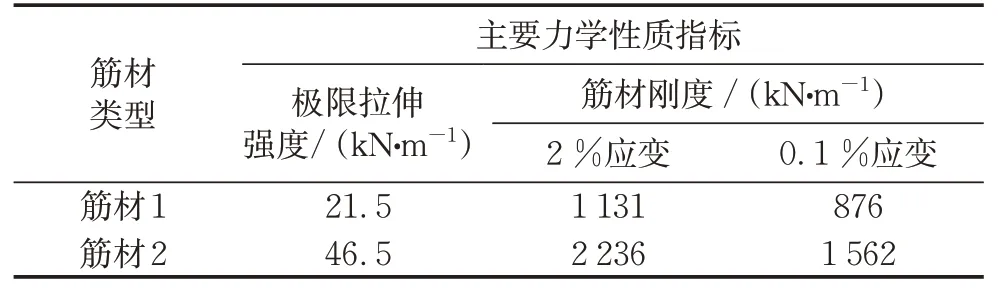
表1 筋材的主要力学性质Tab.1 Mechanic characteristics of reinforcement

1.4 试验方案及过程

如图1所示，选取中间的活动门装置B4作为下拉活动门，即：在试验中下移B4，产生土拱。如表2所示，活动门试验方案共分为两个部分：基准试验（BT1，BT2，BT3和BT4）和局部静荷载试验（ST1，ST2，ST3和ST4）。基准试验是在填料自重作用下进行的，未在填料表面施加荷载。

表2 活动门试验方案Tab.2 Plan of trapdoor test

基准试验中采用的4种布筋方式包括：①无筋材，②垫层下表面铺设一层筋材1，③垫层下表面铺设一层筋材2，④垫层上、下表面各铺设一层筋材1。如表1所示，筋材2的刚度是筋材1的两倍，因此，BT4中两层筋材1的总刚度与BT3中一层筋材2的刚度相等。局部静荷载试验的筋材布置与基准试验相同，局部静荷载试验综合考虑了荷载幅值和筋材布置对土拱的影响。此外，参考试验列于表2的括号内，参考试验中活动门（B4）固定没有下移，无土拱产生。参考试验的目的是测量无土拱产生时作用于活动门上的平均压力，该平均压力将用于计算土拱率（详见1.5节）。

本文活动门试验的具体过程为：在开始填料和铺设筋材前，需将7个活动门装置（B1～B7）的木块调整至同一高度，确保无初始土拱产生。随后，按照试验方案铺设筋材和垫层。将混合好的铝棒相似土分层铺设，每层约20 mm，直至达到填料高度H=256 mm。在基准试验BT1中（无筋情况），活动门（B4）每次下移0.2 mm，直至位移达到8 mm；接着每次下移1.2 mm，直至位移达到30 mm。在其他基准试验BT2，BT3和BT4中（有筋情况），活动门（B4）每次下移0.2 mm，直至位移达到8 mm即可。基准试验中，活动门每下移一次，高速相机拍照一次。局部静荷载试验中，活动门（B4）每次下移0.2 mm直至位移达到8 mm，即局部静荷载p=0阶段。待活动门（B4）下移完成后，通过加载板在填料表面施加静荷载，其加载曲线如图3所示。对填料施加8 kPa荷载维持50 s，拍照一次，卸载50 s，再拍照。然后进入下一阶段。

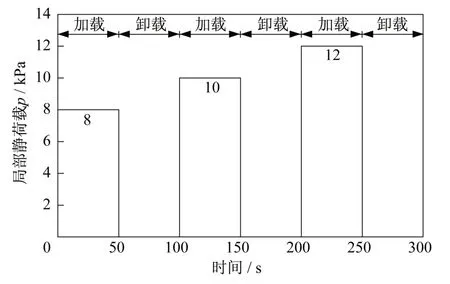
图3 局部静荷载试验加载曲线Fig.3 Loading curve of localized static trapdoor tests

1.5 土拱率的计算

如图4所示，作用在活动门上的平均压力（σ0）可通过式（1）计算：

图4 筋材挠曲段受力分析Fig.4 Force diagram of deflected reinforcement section

式中：B为活动门的宽度，m；d为木块的厚度，m；Ft为布设在活动门下方的力传感器监测所得的力，kN。

作用在筋材挠曲段上方的平均压力（σ1）可通过式（2）计算：

式中：σ1为位于垫层下表面的筋材挠曲段上作用的应力，kPa；T1和T2为位于垫层下表面的筋材挠曲段两端作用的拉力，kN；T1和T2等于PIV技术得到的筋材应变与筋材刚度的乘积。θ1和θ2为位于垫层下表面的筋材挠曲段两端与竖直方向的夹角，（°）。θ1和θ2是根据试验期间拍摄的照片手动测量的。在理想条件下，θ1应等于θ2。然而，在测试中，它们并不总是相等的。

为了定量评价土拱效应，McNulty［3］提出了土拱率ρ，见式（3）：

式中：σv为填料底部作用的平均竖向应力，kPa；γ为填料的容重，kN·m-3；H为填料的高度，m；q为土体表面作用的均布超载，kPa。

本文研究的是局部静荷载作用下土拱效应，故将式（3）修正为式（4）：

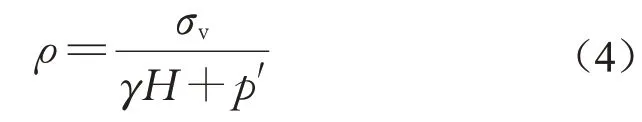
式中：p′为填料表面局部静荷载p传递至填料底部的平均竖向应力，kPa。γH+p′可由表2中参考试验得出。在无筋材的活动门试验中，σv等于作用在活动门上的平均压力σ0。在有筋材的活动门试验中，σv等于铺设在垫层下表面的筋材挠曲段上作用的应力σ1。

2 试验结果与分析

2.1 基准试验结果

基准试验中土拱率ρ随归一化活动门位移（活动门位移与活动门宽度B的比值）的变化曲线如图5所示。如图5a所示，在BT1中，随着归一化活动门位移的增大，土拱率ρ的变化呈现出4个阶段，分别为：初始拱、最大拱、应力恢复及极限状态。这与Chevalier等［4］的研究成果相吻合。图中的竖直虚线分别表示最大拱和极限状态初始点对应的归一化活动门位移，其值分别为1.25%和10.55%。

对于加筋试验，在活动门位移达到8 mm之前，筋材均与活动门脱离。由图5b和5c可见，BT2和BT3中筋材发生脱离所对应的归一化活动门位移分别为2.50%和2.03%。当活动门继续下移时，筋材拉伸变形已稳定，铺设在垫层下表面的筋材挠曲段上作用的应力σ1并未改变，因此土拱率保持不变。在BT2和BT3中，土拱率ρ均随着归一化活动门位移的增加而减小到最小值，随后小幅增大，最后保持稳定。与BT1相比，有筋情况下土拱几乎不存在应力恢复阶段，表明了筋材限制了土拱的退化。对比图5b和5c可以发现，BT2中土拱率的稳定值与BT3的大致相等，意味着在填料自重的情况下，筋材刚度对土拱率的影响并不显著。图5b和5c中归一化筋材最大挠度Δ是指筋材的最大挠度与活动门宽度B的比值。可以看出，BT3中归一化筋材挠度均小于BT2，表明筋材刚度越大，其变形越小。如图5d所示，当归一化活动门位移达到2.19%时，下层筋（垫层下表面筋材1）与活动门脱离。对比图5c和d可以发现，BT4的土拱率ρ变化规律与BT3的相同。并且，BT4中下层筋材1的归一化挠度最大，BT3中筋材2的次之，BT4中上层筋材1最小。BT4中上、下两层筋材1的平均归一化挠度与BT3中筋材2的相同。总而言之，在填料自重条件下，BT3和BT4的土拱率及筋材变形没有显著区别。换言之，在填料自重荷载下，当筋材总刚度相等时，不同的筋材布置方式对土拱率及筋材变形的影响不大。

自重作用下BT1的填料位移云图如图6所示，填料内部以及表面均存在一定位移，即不存在等沉面。因此，在利用Terzaghi［1］模型求解土拱率时，采用无等沉面作为边界条件。图5中的水平实线表示水平土压力系数K取值不同时使用Terzaghi［1］计算公式求得的土拱率ρ。其中，陈若曦等［13］建议采用Kchen=（1+Kp·tan2θ）/（tan2θ+Kp）=1.43（Kp为朗肯被动土压力系数，θ=45°+φ/2）；Terzaghi［1］建议 采 用K=1；Ladanyi和Hoyaux［14］建 议 采 用Krynine= cos2φ/（1+sin2φ）= 0.70；Marston和Anderson［15］建议采用朗肯主动土压力系数Ka=（1-sinφ）/（1+sinφ）=0.41。如图5a所示，对于BT1来说，采用Krynine和Ka计算求得的土拱率明显大于极限状态下土拱率的试验值，K=1求得的土拱率与极限状态下土拱率的试验值吻合较好，Kchen则小于土拱率试验值。对于加筋试样来说，其极限状态对应的土拱率试验值均小于Kchen计算得到的土拱率，即Kchen计算值可用于保守估计土拱率。

图5 土拱率、归一化筋材最大挠度与归一化活动门位移的关系Fig.5 Soil arching ratio and maximum normalized reinforcement deflections versus normalized trapdoor displacements

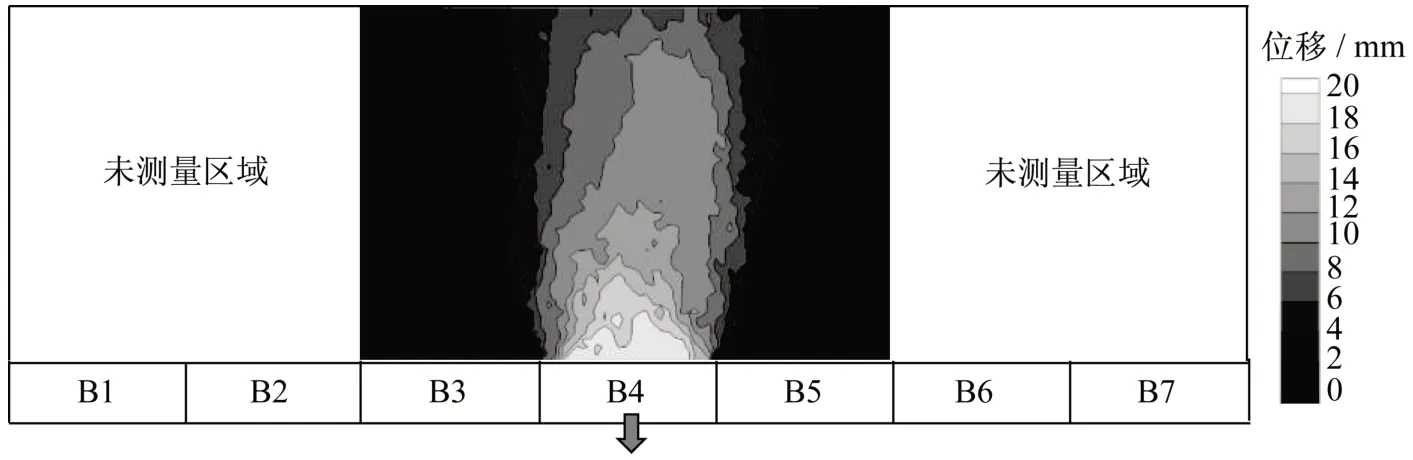
图6 填料自重作用下BT1填料位移云图Fig.6 Displacement contour of the backfill in BT1 under self-weight

2.2 局部静荷载试验结果

2.2.1筋材拉力

由于PIV测量得到的筋材应变均小于0.1%，故选用表2中0.1%应变对应的筋材刚度计算得出筋材拉力。与图3的局部静荷载试验加载曲线相对应，图7中“加载”是指填料表面施加局部荷载，“卸载”是指填料表面移除局部荷载。局部静荷载p=0对应活动门（B4）下移完成、施加局部荷载前。

从图7可以看出，局部静荷载的施加导致了筋材拉力的增大。随着荷载的增大，筋材拉力逐步增大，且加载阶段筋材拉力的增大速度远大于卸载阶段。从图7a和7b可以看出，在加载阶段，ST3中筋材2的拉力略大于ST2筋材1的拉力，在卸载阶段，两者的拉力基本保持相等。因此，在加载阶段，刚度较大的筋材会导致较大的拉力。对比图7c和7d可知，ST4中上层筋材1的拉力明显小于下层筋材1。图7e是ST4中垫层上、下表面两层筋材1拉力的合力。比较图7b和7e，ST4中上、下两层筋材1的总拉力大于ST3中筋材2的拉力，意味着当ST3和ST4中筋材总刚度相等时，ST4中两层筋材1的布置方式使筋材拉力得到了更大的发挥。

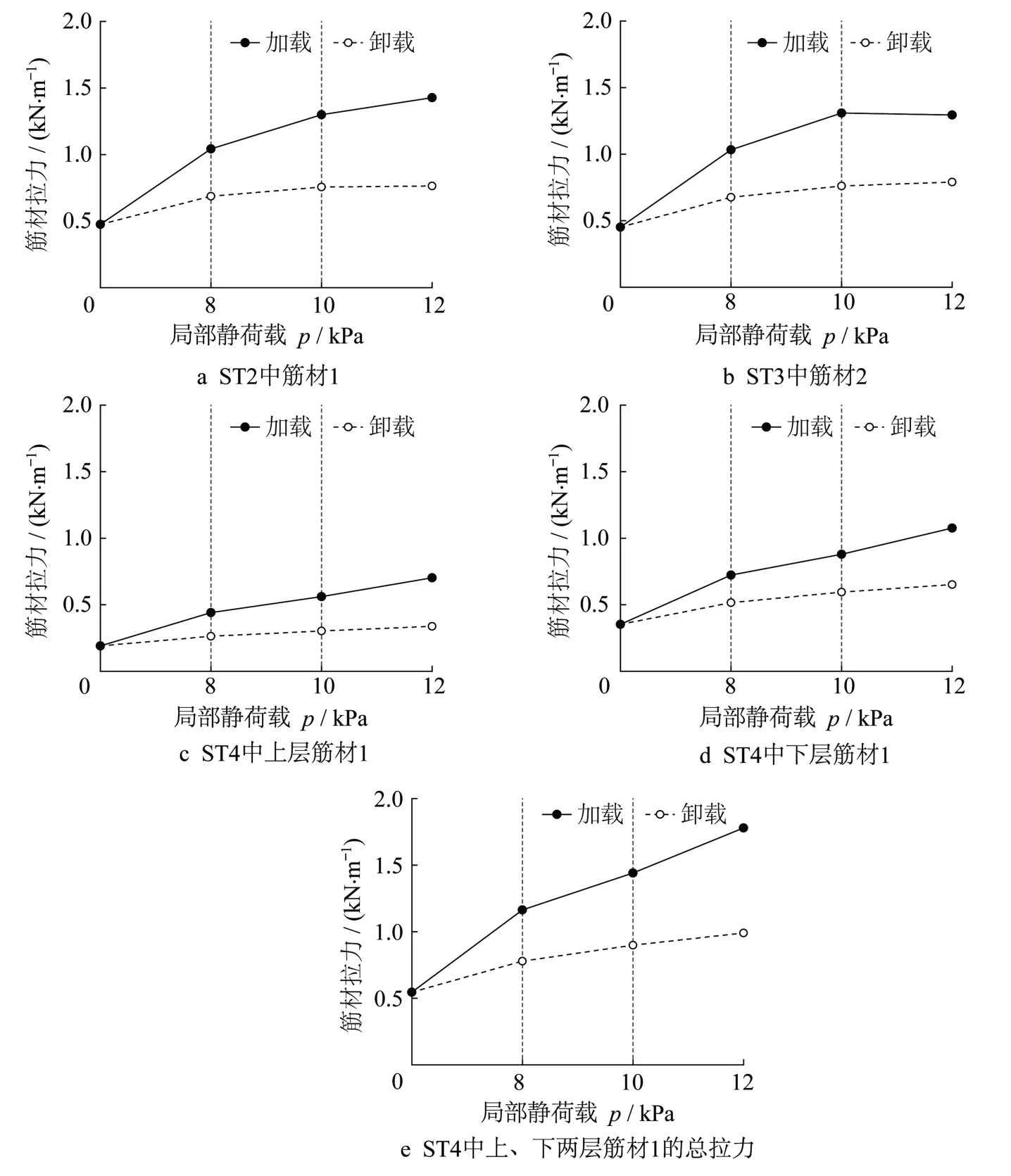
图7 不同阶段对应的筋材拉力Fig.7 Variations of tensile forces of reinforcement in different stages

2.2.2土拱率的变化

图8展示了局部静荷载作用下活动门试验各个阶段的土拱率ρ，分别为：局部静荷载p=0阶段（ρ0），加载阶段（ρj）和卸载阶段（ρx）。如图8a所示，在ST1中（无筋材情况），加载和卸载阶段的土拱率（ρj、ρx）明显大于8 mm位移阶段的土拱率（ρ0），表明局部静荷载对土拱效应有削弱作用。并且，土拱率（ρj、ρx）随着荷载的增大而增大，意味着荷载越大，对土拱的削弱作用越明显。更重要的是，ST1中加载阶段的土拱率均大于卸载阶段（ρj＞ρx），说明土拱效应在卸载阶段有一定的恢复。

加筋试验的土拱率变化如图8b、8c和8d所示，加载和卸载阶段的土拱率均随着荷载的增加而增加。与不加筋试验（ST1）相比，加筋试验中加载和卸载阶段的土拱率（ρj、ρx）均小于不加筋试验。这说明，筋材可有效地抑制由局部静荷载引起的土拱效应的退化；换言之，筋材增强了土拱抵抗荷载的能力。另外，加筋试验中，加载的土拱率小于卸载阶段的土拱率（ρj＜ρx），该现象与不加筋试验完全不同。土拱效应本质上是由于填料中活动门上方的活动区和稳定区的相对位移引起的；在卸载阶段，活动门与稳定区上方的填料与筋材都发生回弹。由于筋材铺设在垫层底部，则填料的回弹受限于筋材的回弹。根据PIV结果，筋材的回弹大于填料的回弹；因此，活动门与稳定区之间填料相对位移减小，导致原来由筋材传递到稳定区填料的应力转移至活动门上方填料，从而在卸载阶段削弱土拱效应，具体表现为ρj＜ρx。

比较图8b和8c可以发现，ST2中加载阶段的土拱率（ρj）略大于ST3，同样地，ST2中卸载阶段的土拱率（ρx）明显大于ST3。该结果说明，筋材刚度增大可有效提高土拱抵抗静荷载的能力。如图8c和8d所示，ST4中加载和卸载阶段的土拱率（ρj、ρx）均小于ST3。在ST4中，上层筋材1发挥张力膜效应，导致作用在下层筋材1上的竖向应力减小。因此，在ST3和ST4两者筋材总刚度相等的情况下，ST4中两层筋材1的使用更多地促进了上层筋材1的张力膜效应的发挥，从而减小了土拱效应的退化。

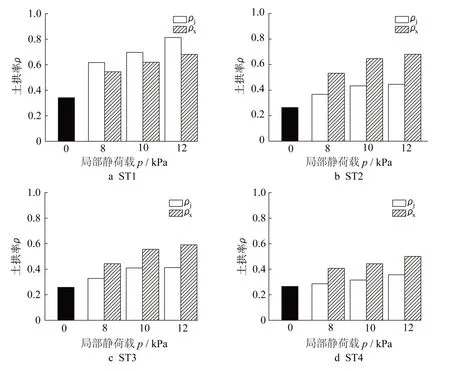
图8 局部静荷载作用下土拱率的变化Fig.8 Variations of soil arching ratios in trapdoor tests under static loading

3 理论计算

图9a为局部静荷载p=8 kPa作用下ST1填料的竖向位移云图。局部静荷载p=10和12 kPa时，PIV分析所得填料内部位移云图与图9a相似，基于篇幅原因略。从图9a中可以看出，填料内部出现了一系列倾斜的滑裂面，与Terzaghi假设的填料自重作用下的垂直滑裂面不同［1］，其主要原因是加载板的长度L远大于活动门宽度B（L=3B）。因此，本文假设局部静荷载作用下填料内部存在两条倾斜的滑裂面，定义滑裂面与水平方向的夹角为αp。如图6所示，在填料自重作用下，滑裂面与水平方向夹角αp接近90°；如图9a所示，在局部静荷载p=8 kPa作用下，该滑裂面从活动门（B4）两端出发一直延伸到加载板的两端。根据加载板长度L与填料高度H的几何关系可得，αp=arc tan（2）=63.4°。在局部静荷载p=10和12 kPa时，PIV分析所得滑裂面与水平方向夹角αp未发生明显变化。由此可以推断，当局部静荷载p由0缓慢增长至8 kPa时，αp随之发生变化；当局部静荷载p大于8 kPa后，αp保持不变。

局部静荷载作用下滑裂面内高度为h的填料单元受力图如图9b所示，同时假设：①活动门上方或筋材挠曲段上方的竖向应力是均匀分布的；②侧向土压力系数K是常数；③假定滑裂面与水平方向的夹角αp随局部静荷载p的关系如式（5）所示：在局部静荷载p小于8 kPa时，夹角αp（°）与局部静荷载p（kPa）呈线性关系；在局部静荷载p大于等于8 kPa时，夹角αp保持不变。

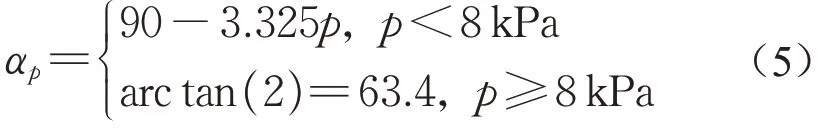
通过倾斜滑裂面内高度为h的填料单元的竖向受力平衡可得：

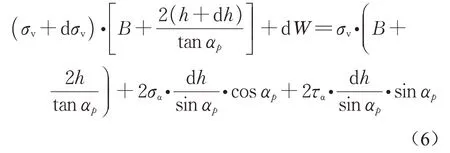
其中，填料单元的自重dW计算如下：

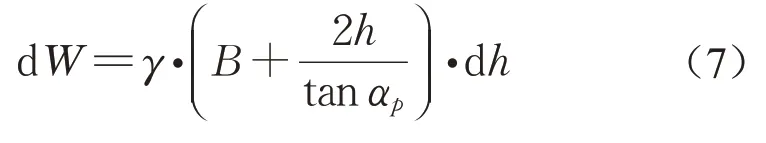
依据主应力轴旋转，倾斜滑裂面上的法向应力与切向应力如下式（8）和（9）所示：

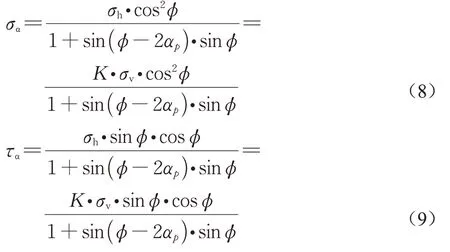
将式（7）、（8）和（9）代入式（6），略去高阶微分量，化简可得：

代入边界条件式（11），求解式（10）得：

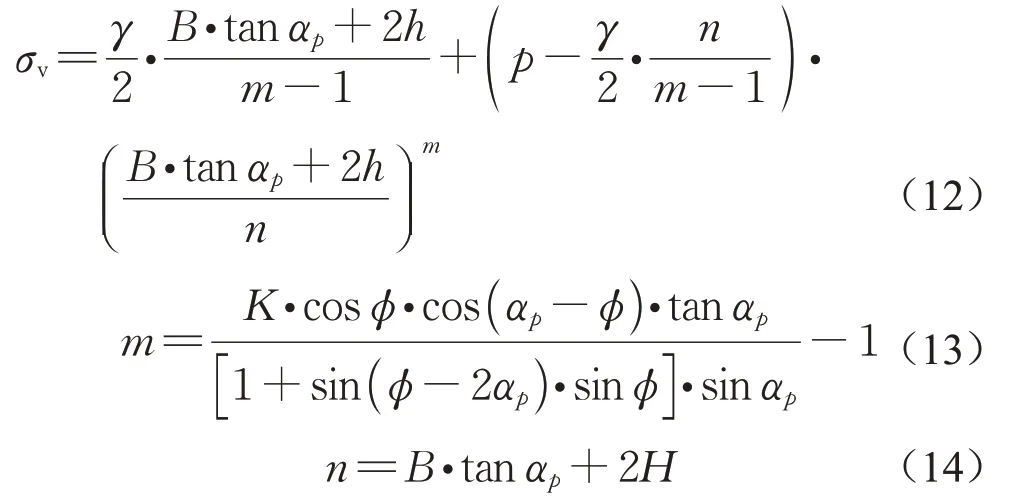
式（12）—（14）中：σv为填料活动区单元体的竖向压力，kPa；B为活动门宽度，B=128 mm；γ为填料容重，γ=22.4 kN·m-3；φ为填料内摩擦角，φ=25°；K为侧向土压力系数；h为距离活动门的高度，m；H为填料高度，H=2B=256 mm；p是填料表面局部静荷载，kPa，如图3所示，p=8，10，12 kPa；αp是滑裂面与水平方向的夹角，（°）。

因此，当h=0时，活动门（B4）上方（不加筋情况）或筋材挠曲段上方（加筋情况）由局部静荷载导致的竖向附加压力Δσv可根据式（15）计算：

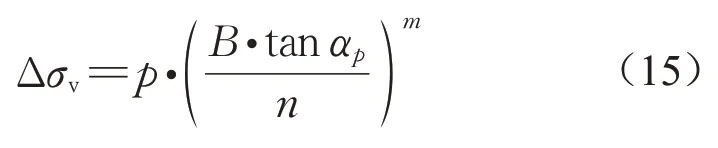
值得注意的是，Δσv仅仅由局部荷载引起，并不包含填料自重作用下的竖向压力。

将2.1节提及的4个不同的侧向土压力系数K代入式（15）可得图10中4条曲线，并与相应的试验数据进行对比。从图10中可以看出，对于无筋试验（ST1），当K=Ka时，式（15）可较好地预测ST1中活动门（B4）上由局部静荷载导致的竖向附加压力（Δσ0）；其他三个侧向土压力系数（K=Krynine，K=1，K=Kchen）都严重低估了该附加压力（Δσ0）。对于有筋试验（ST2，ST3和ST4），当K=Ka时，式（15）计算的Δσv明显大于试验中筋材挠曲段上由局部静荷载导致的竖向附加压力（Δσ1）。当K=1，K=Kchen时，式（15）均低估了Δσ1。当K=Krynine时，式（15）略微高估了Δσ1。因此，K=Krynine可较合理地预测筋材挠曲段上由局部静荷载导致的竖向附加压力（Δσ1）。

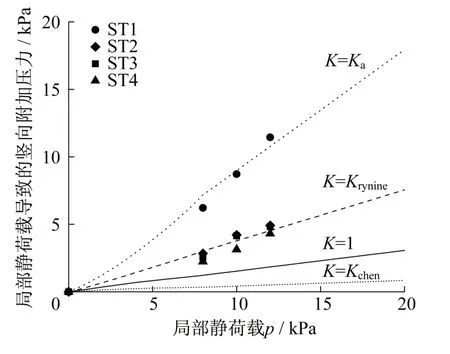
图10 活动门（B4）上方或筋材挠曲段上方由局部静荷载导致的竖向附加压力：试验和理论计算对比Fig.10 Comparison of predicted additional vertical stresses induced by localized surface loading with the additional average pressures on the central trapdoor or on the deflected reinforcement section

4 局限性

本试验采用铝棒相似土作为填料，铝棒相似土与土压力计的线接触形式导致土压力计读数不可靠，因此无法实现通过在填料内布置土压力计进而获得活动门上方或筋材挠曲段上方的竖向应力的分布特征。在本文的活动门试验装置中，通过在活动门木块下方设置单个力传感器，采用式（1）及式（2），反算出活动门的平均压力（σ0）和作用在筋材挠曲段的平均压力（σ1）。因此在理论计算中，采用“活动门上方或筋材挠曲段上方的竖向应力均匀分布”这一假定，进而可与试验数据进行对比以验证本文提出的理论计算方法是否合理。此外，由于本研究的局部静荷载第一级加载幅值为p=8 kPa，缺少p=0～8 kPa这一范围内滑裂面与水平方向夹角αp的变化规律，因此在理论计算中，依据现有试验结果，采用式（5）描述滑裂面与水平方向的夹角αp随局部静荷载p的变化关系。这些局限性拟在后续研究中改进。

5 结语

本文通过平面应变活动门试验研究了填料自重和局部静荷载作用下筋材对土拱效应的影响；填料选用铝棒相似土；采用了4种不同的筋材布置方式：①无筋材；②垫层下表面铺设一层筋材1；③垫层下表面铺设一层筋材2；④垫层上、下表面各铺设一层筋材1；垫层厚度与活动门宽度比值为0.175。筋材2的刚度约是筋材1的两倍，因此，筋材铺设方式③和④的总刚度相等。本文得到以下结论：

（1）在填料自重作用下，由于筋材的存在，土拱几乎不存在应力恢复阶段。无论是否加筋，局部静荷载导致了土拱有明显的退化现象。在加载阶段，与无筋试验相比，筋材的使用限制了土拱的退化；在卸载阶段，与无筋试验不同，由于筋材的回弹大于填料的回弹，土拱效应将持续退化。

（2）在填料自重作用下，筋材刚度对土拱效应的影响并不明显。然而，在局部静荷载作用下，刚度大的筋材可明显减小卸载阶段土拱效应的退化。

（3）在填料自重作用下，筋材总刚度一致时，不同的筋材布置方式对土拱效应的影响不大。在局部静荷载作用下，比起使用单层高刚度筋材，双层低刚度筋材的使用，促使筋材拉力得到更大的发挥，增强了上层筋材的张力膜效应，因此减弱了局部静荷载对土拱效应的削弱作用。

（4）填料自重作用下，采用水平土压力系数K取值为1的Terzaghi［1］计算公式可以较好地预测无筋情况下的土拱率，采用K取值为Kchen的Terzaghi［1］计算公式可保守估计有筋情况下的土拱率。

（5）本文提出了预测活动门上方（不加筋情况）或筋材挠曲段上方（加筋情况）由局部静荷载引起的竖向附加应力的理论计算方法。由于本试验中施加局部静荷载p的加载板长度远大于活动门宽度，本文提出的理论方法对滑裂面与水平方向的夹角αp随局部静荷载p的变化关系进行了假定。结果表明，采用Ka和Krynine可以分别合理地预测活动门上方（不加筋情况）和筋材挠曲段上方（加筋情况）由局部静荷载引起的竖向附加应力。

作者贡献声明：

李格烨：数据处理，论文撰写、修改、意见回复。

徐超：提出研究方向，学术指导，论文审阅。

沈盼盼：学术指导，论文修改、意见回复。

张兴亚：试验指导。

罗敏敏：学术指导。

梁程：学术指导。