长三角G15氢能高速公路加氢站布点建模

吕 洪，郑乾辉，周 伟，张存满

（1.同济大学汽车学院，上海 201804；2.同济大学新能源汽车工程中心，上海 201804）

氢能作为一种清洁、高效、安全的新能源，被视为21世纪最具发展潜力的清洁能源之一，氢燃料电池汽车作为氢能应用的最主要途径，相比于传统燃油车，具有污染小，零排放的优点。加氢基础设施是氢燃料电池汽车的能源补给站，对燃料电池汽车的发展和推广过程至关重要。截止2020年底，中国已建成加氢站118座，根据《节能与新能源汽车发展技术路线图2.0》中的规划，到2025年，我国计划建成1 000座加氢站。

加氢站建设成本高，对周边环境有安全间距的要求，因此，加氢站的布点具有一定的局限性。在燃料电池汽车发展的导入期，针对我国燃料电池汽车发展和示范的特点，结合未来市场化运营，建立加氢站布点理论模型，进行科学合理的加氢站布点，具有较好的创新性和实际应用价值。

在国外，已经有了不少学者对加氢站布点模型进行了研究。在加氢站实地布点模型方面，主要分为基于点和基于流动的模型两类［1］，在Itaoka等［2］和Kuby等［3］的研究中，根据调查的结果，分别对基于点和基于流动的模型中司机的加氢行为理论进行了总结——基于点的模型更加符合传统燃油车车主的加油习惯；而对天然气车主的调查显示，在面对稀疏的站点时，他们加气会更加谨慎且愿意绕道，这更符合基于流动的模型。在基于点的模型中，氢气需求位于网络中的节点上，最常用的是p-median模型［4］，其最著名的应用是美国Advanced Power and Energy Program中加州大学所研发的STREET模型［5］，它以基于点的模型为基础，结合GIS软件实现可视化的输出，最后应用于美国加州的加氢站布点。在基于流动的模型中，氢气需求位于网络中的路径上，这类模型最早由Hodgson等［6］提出，Kuby等［7］引入续航里程因素并应用于加氢站布点，提出FRLM模型，此后，一些学者在这基础上又引入站点加注能力［8］、路径偏离［9］等因素，提出CDFRLM模型［10］。对于这两类模型，Honma等［11］也进行了比较，给出了各自的特点。

此外，在模型中，常常要对氢气的成本进行优化，这也会牵涉到氢气生产、运输、加注等各个环节，由此诞生了氢供应链网络模型，该模型由Almansoori等［12］于2006年首先提出，此后，在这类模型中，引入了多周期阶段性布点［13］、氢气需求不确定性［14］、可再生能源制氢［15］等因素的考虑，目标函数也从引入了碳排放［16］、环境污染［17］、安全风险［18］等考量。Li等对这类模型做了一个系统的综述［19］，并在法国利用该模型进行了全面的案例分析［20］。

在国内，关于加氢站布点方面的研究还比较少。Lin等［21］采用人口、收入、教育水平等多数据源估算北京市各区的氢气需求，并采用p-median模型进行布点。孙浩然［22］用全生命周期的方式，考虑多氢源供氢的方式，对氢气从氢源到加注的成本建立了模型，用粒子群算法优化氢气运输与高速公路加氢站位置。但在其的研究内容中，各个加氢站的加注能力作为外源性输入，并未考虑燃料电池汽车车辆特性和加氢站加注技术特性，对于加氢站本身成本的建模也较为简单，只是粗略地将成本分为建设成本和运营成本，各取了一个固定值，未进行细化。故本文以高速公路上的加氢站布点建模作为研究内容，在孙浩然［22］的研究基础上，进一步优化了加氢站建设运营经济性模型，并将站点加注能力和加氢站位置都作为优化对象，通过综合考虑加氢站加注能力、加氢站建设成本和燃料电池汽车运行特性，应用线性规划求解进行最优匹配，开展高速公路的加氢站布点建模研究，并对长三角G15上海到盐城段高速公路开展实例布点。

1 快速路一维道路加氢站布点模型建立

1.1 模型边界条件

本文主要对高速公路上加氢站的布点进行建模分析。以最小化加氢站的亏转盈年限为目标函数，约束条件主要包括相邻加氢站的距离限制、加氢站的加注能力限制、数量限制、氢源的氢气产量限制等。模型的输入包括上述约束条件的边界值、加氢站的成本参数、不同地域的用地价格、氢源的位置及氢气价格、油氢合建站、高速公路上热点城市的位置及城市间氢气需求量及其随机性、加氢站候选点等，模型的输出包括加氢站的位置、加注能力及氢气购入方案和相应的目标函数值等。

根据对随机性处理的不同，模型给出两类方案，用户可根据需要选择其中的一类，①鲁棒性方案，即在加氢站的建设能够满足极端情况下用户的氢气需求的前提下，优化经济性；②在考虑流动随机性下，以经济性最优为唯一目标进行优化。

1.2 加氢站建设运营经济性模型

本文引入净现值方法建立加氢站建设运营经济性模型，成本分类及符号含义可见表1。成本主要包含加氢站建设初始投资和运营成本。初始投资包括土地购置与基建成本（含用地成本、建设成本）和设备购置成本（含压缩机、储氢瓶、加氢机、系统安装成本）；运营成本包括人工成本、设备维护成本、能源消耗成本（含用电成本、其他能源成本）、氢气购入成本、税收等其他成本占比。加氢站的收入主要包括氢气出售。

模型假设加氢站规模基本一致，因此，各加氢站的用地面积、加氢机数量、系统安装、设备维护成本、人工成本、税收及其他成本占比也可视为定值，而对于某一地点而言，土地单价Plan也是基本固定的。因此，将成本分为4类：

（1）与加氢站加注能力P相关成本CP，包括压缩机和储氢瓶成本，由式（1）计算：

式中：ρ为氢气密度；β为加氢站的储氢量与站点加注能力的比值，与加氢站的加注策略相关；Qcom为压缩机单位时间的流量；Tcom为压缩机日工作时间；Pcom为单个压缩机的成本；Qsto为单个储氢瓶的储氢量；Psto为单个储氢瓶的成本；

（2）与加氢站氢气出售量Qhyd相关成本CQ，包括氢气购入成本和压缩机用电成本，由式（2）计算：

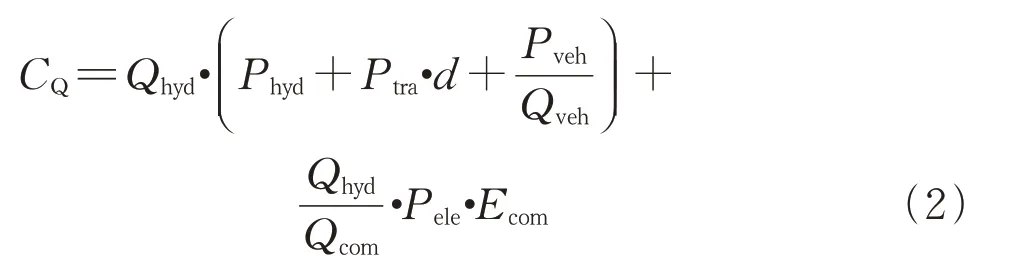
式中：d为运输距离；Phyd为单位氢气的购入成本；Ptra为单位距离单位质量氢气的运输成本；Pveh为单辆管束拖车的租赁成本；Qveh为单辆管束拖车的运氢量；Pele为电价；Ecom为压缩机单位时间的耗电量。

（3）与地域有关：如用地成本，等于Plan·Slan。Slan为加氢站占地面积。

（4）其他成本可视为定值，包括投资固定成本CFcap（含建设成本、加氢机成本、系统安装成本）和运营固定成本CFope（含人工成本、设备维护成本、其他能源成本）。

经济性分析要考虑成本和收入两方面，因为加氢站的经营是一个长期的工作，往往要好几年才能实现成本回收。因此，成本分析还引入了折现率α，用来表示时间效应带来的影响。净现值Cnpv计算如式（3）所示：

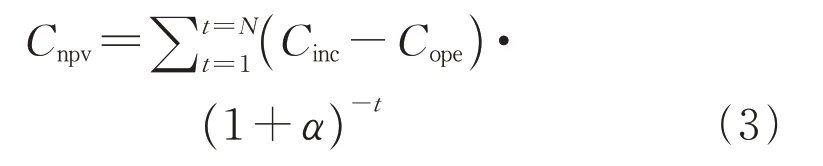
式中：Cinc为加氢站的年收入；Cope为加氢站的年运营成本；t为年份。

当Cnpv超过加氢站的初始投资Ccap时，以此时的亏转盈年限N来衡量经济性。

本文也考虑了油氢合建站对成本的影响。对于允许油氢合建站的地点，由于土地和人员可与加油站共用，故在成本计算中不考虑土地成本和人工成本。

考虑到亏转盈年限是离散的，不同的布点方案可能计算得到的亏转盈年限是相同的，故在计算中引入了另一个概念——投资利润率（本文取其倒数）Cpir来作为目标函数，如式（4）所示：

可以看到，对于经济性，Cpir和亏转盈年限有着相同的变化趋势。

1.3 快速路一维道路加氢站布点数学模型

在模型中，为了描述各点的相对位置，需要引入坐标系［22］。选取高速公路作为坐标系的横轴，将高速公路外的某点（氢源）行驶到高速公路上时所经过的路程为纵坐标。模型定义，热点城市和加氢站候选点的纵坐标都为零，即位于横轴上。由此，可得两点的之间的距离等于两点横坐标差的绝对值加上两点的纵坐标。

模型的目标函数如式（5）：

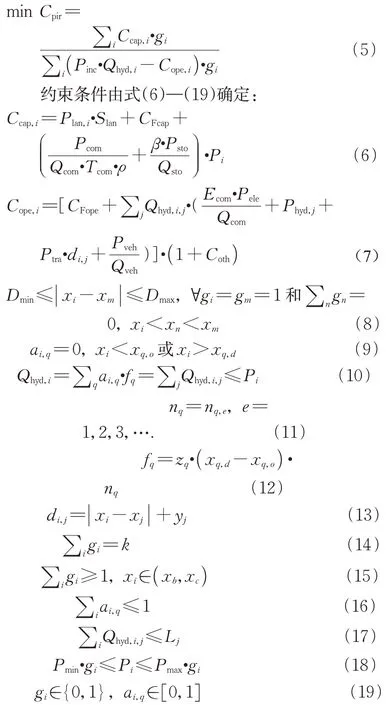
式（6）—（19）中：i，m，n均为加氢站候选点索引；j为氢源索引；Pinc为加氢站氢气售价；Coth为税收等其他成本占运营成本的比重；x，y为点的横坐标与纵坐标；gi为决策变量，当i处建立加氢站时为1，否则为0；q为流动索引，即起点城市和终点城市相同的车辆集合；b，c为流动起点和终点的热点城市索引；Dmin，Dmax分别为相邻加氢站距离所允许的最小值与最大值；ai，q为流动q在i处加氢的车辆占比；zq为流动q中车辆的单位距离氢耗；xq，o，xq，d为流动q的起点与终点；nq为流动q中的汽车数量，nq，e表示流动q可能的汽车数量，表示随机性的影响；fq为流动q的氢气需求；k为给定的加氢站数量；Lj为氢源j的最大产量；Pmax，Pmin分别为加氢站的最大与最小加注能力。

式（5）是模型的目标函数，表示要使加氢站整体的Cpir最小；式（6）表示加氢站i初始投资成本的计算，对同一地点而言，是Pi的一次函数；式（7）表示加氢站i年度运营成本的计算，是Qhyd，i，j的一次函数；式（8）表示相邻站点之间距离要满足距离限制；式（9）表示若加氢站不在该流动的路径上，该流动不能在该处加氢；式（10）表示加氢站的氢气出售量等于所有需求在该站点的加氢量之和，且不大于该站点的加注能力；式（11）表示流动的随机性因素，当求鲁棒性方案时，取其中的最大值；式（12）表示流动的氢气需求等于其中的车辆在行驶过程中的氢气消耗量；式（13）表示氢气运输距离的计算；式（14）表示加氢站的数量限制；式（15）表示相邻的热点城市间至少存在一个加氢站；式（16）表示车辆在行驶途中至多只加一次氢气；式（17）表示氢源的氢气出售量不能超过氢源的产量；式（18）是加氢站加注能力的边界限制；式（19）是变量的取值范围。

1.4 算法设计

加氢站数量和位置主要由式（8）和式（14）的约束，约束条件较多，故采用穷举法求解。列举符合约束的站点位置组合，并将相邻热点城市间的高速作为路段（路段数记为r），在每种站点位置组合中，记录加氢站在各路段上的分布。

由目标函数可知，氢气在能够全部售卖的前提下，加氢站建设得越大，更加容易回本。当加氢站加注能力大于氢气出售量时，多余的加注能力不会提升收入，但会增加成本。当氢气出售量等于加氢站加注能力时，加氢站的效益最好。因此，模型约束条件要最大化氢气出售量，故对于含变量ai，q的约束，转化为不等式：

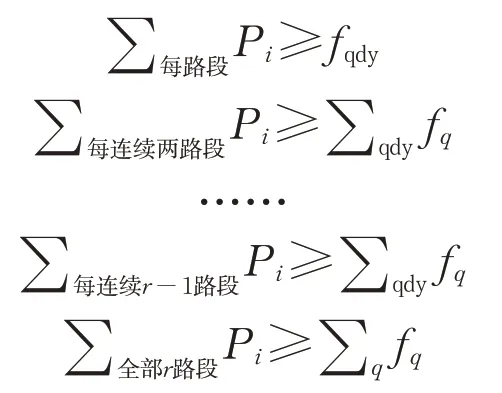
其中，连续路段指其中的路段能在高速路上形成一条连续的路段集合，不等式左边是对这些路段上的站点加注能力进行求和；下标“qdy”表示起点城市和终点城市都在不等式左边的连续多个路段上的流动，不等式右边对这些流动进行求和。这一系列不等式能保证每个流动的氢气需求都能被完全满足。

在目标函数方面，因氢气出售量等于所有流动的需求之和，故收入为定值，只需要最小化成本。在给定站点位置组合前提下，初始投资Ccap，i为Pi的一次函数，运营成本Cope，i为Qhyd，i，j的一次函数，此外，根据实际条件下的计算结果，减少初始投资（主要指设备购置成本）往往比减少运营成本（主要指氢气购入成本中的氢气运输部分）更能满足经济性要求（除非运输距离相当大），故目标函数可以改为式（20）：

式中：w为大权重；v为小权重。这样可以使目标函数在优化过程中，首先将初始投资Ccap，i最小化，然后再将运营成本Cope，i最小化。

目标函数和约束条件都转化为Qhyd，i，j和Pi的线性关系，可用线性规划的方式求解。

在鲁棒性方案中，要满足任意情况下的氢气需求，故各流动取最大值，故只需要通过前两个步骤就能够解决。在考虑流动随机性时，流量不确定，故通过粒子群算法先假设各流动对应的氢气需求，然后根据前两步计算目标函数。多次迭代，进行优化。整个算法流程如图1所示。

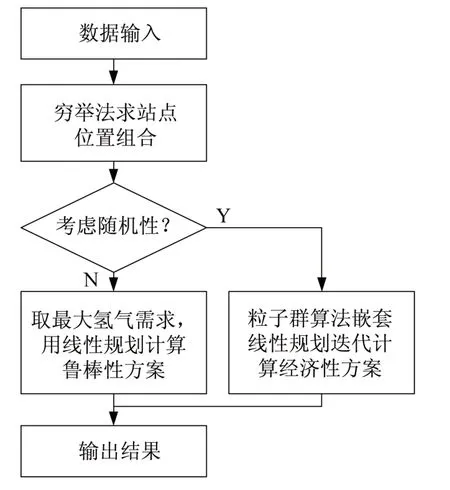
图1 算法流程Fig.1 Flowchart of the algorithm

1.5 实例分析

本文以上海、苏州、南通、如皋、盐城为燃料电池汽车发展热点城市，开展在G15沈海高速上海—盐城段进行加氢站的布点研究。

首先建立坐标系。选择以上海（上海G15嘉西收费站）为原点，上海—盐城为横轴正方向，则各热点城市的坐标（单位：km）为上海（0，0），苏州（常熟开发区收费站）（53，0），南通（兴仁收费站）（89，0），如皋（如皋收费站）（140，0），盐城（盐城南收费站）（259，0）

加氢站的候选点主要选取在服务区，建设油氢合建站（单位：km）：太仓沙溪服务区（32，0），苏通大桥服务区（68，0），先锋服务区（83，0），如皋服务区（122，0），东台服务区（177，0），大丰服务区（230，0）。

加氢站经济模型相关参数如表1所示。考虑到3：2：1的三级加注策略是加氢站常用的一种加注策略，最低一级可通过管式拖车代替，其余两级需要加氢站加压后储存，故加氢站储氢量占比取0.84。

表1 加氢站成本参数Tab.1 Cost parameters of hydrogen refueling station

当前中国的燃料电池汽车主要应用于商用车和物流车，本模型的车流量数据以城际交通的大巴车作为研究对象，车流量统计包含热点主城区及其周边区域，模型以上海—苏州、上海—南通、上海—如皋三条路线的城际公交车为含随机性因素对象，假设燃料电池汽车的数量占总公交车数量的10%，车辆氢耗取0.08 kg·km-1。在出行周期内，模型假设每辆车加氢一次。车流量信息如表2所示。

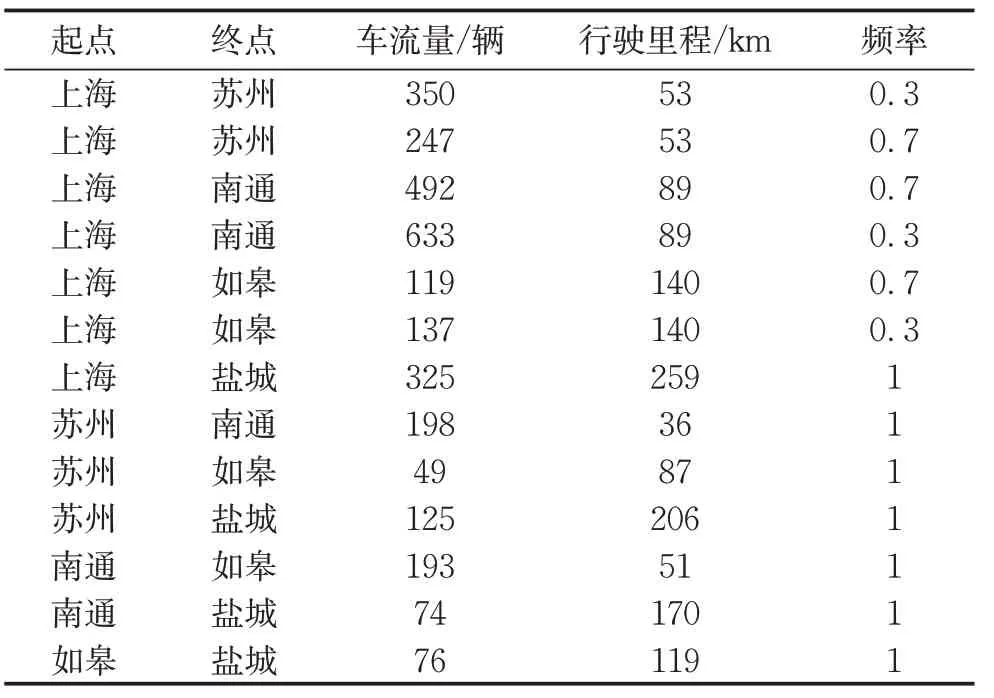
表2 热点城市间的车流量信息Tab.2 Traffic flow data between cities

关于长三角地区的制氢厂信息如表3所示，其中，氢气价格统一取2.5元·N·m-3，制氢厂的年运营时间为8 000 h。

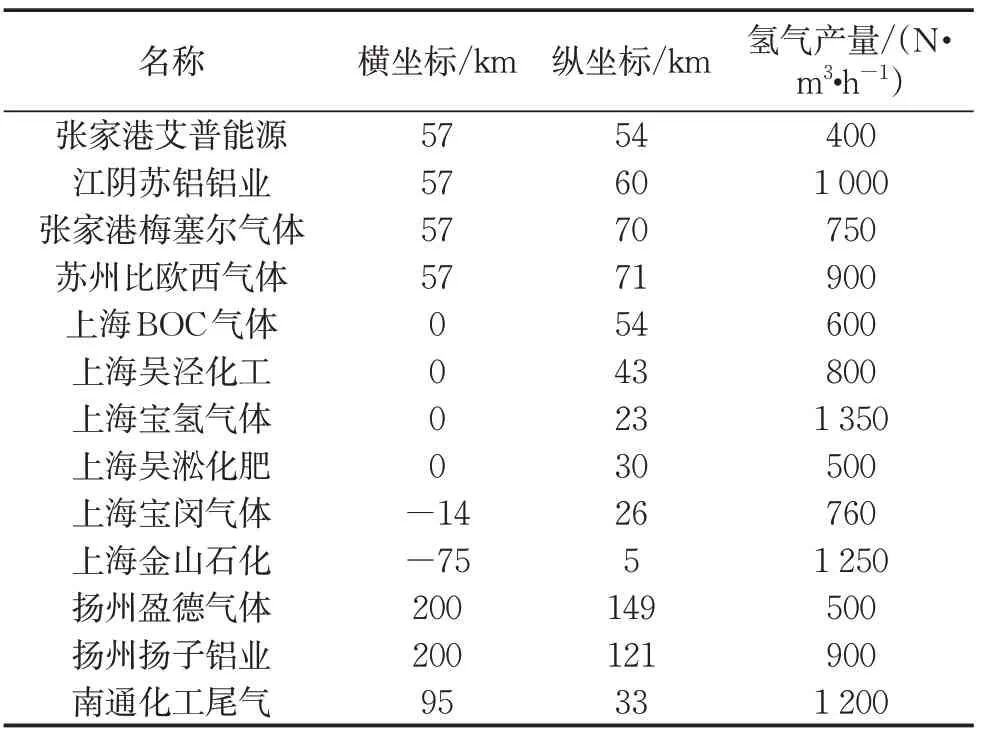
表3 长三角地区氢源信息Tab.3 Hydrogen source data in Yangtze River Delta

边界条件来自于长三角氢走廊建设发展规划：相邻加氢站最小和最大距离分别为20和100 km，加氢站加注能力下限和上限分别为400和1000 kg·d-1，加氢站数量为4座。热点城市、服务区、制氢厂分布如图2所示

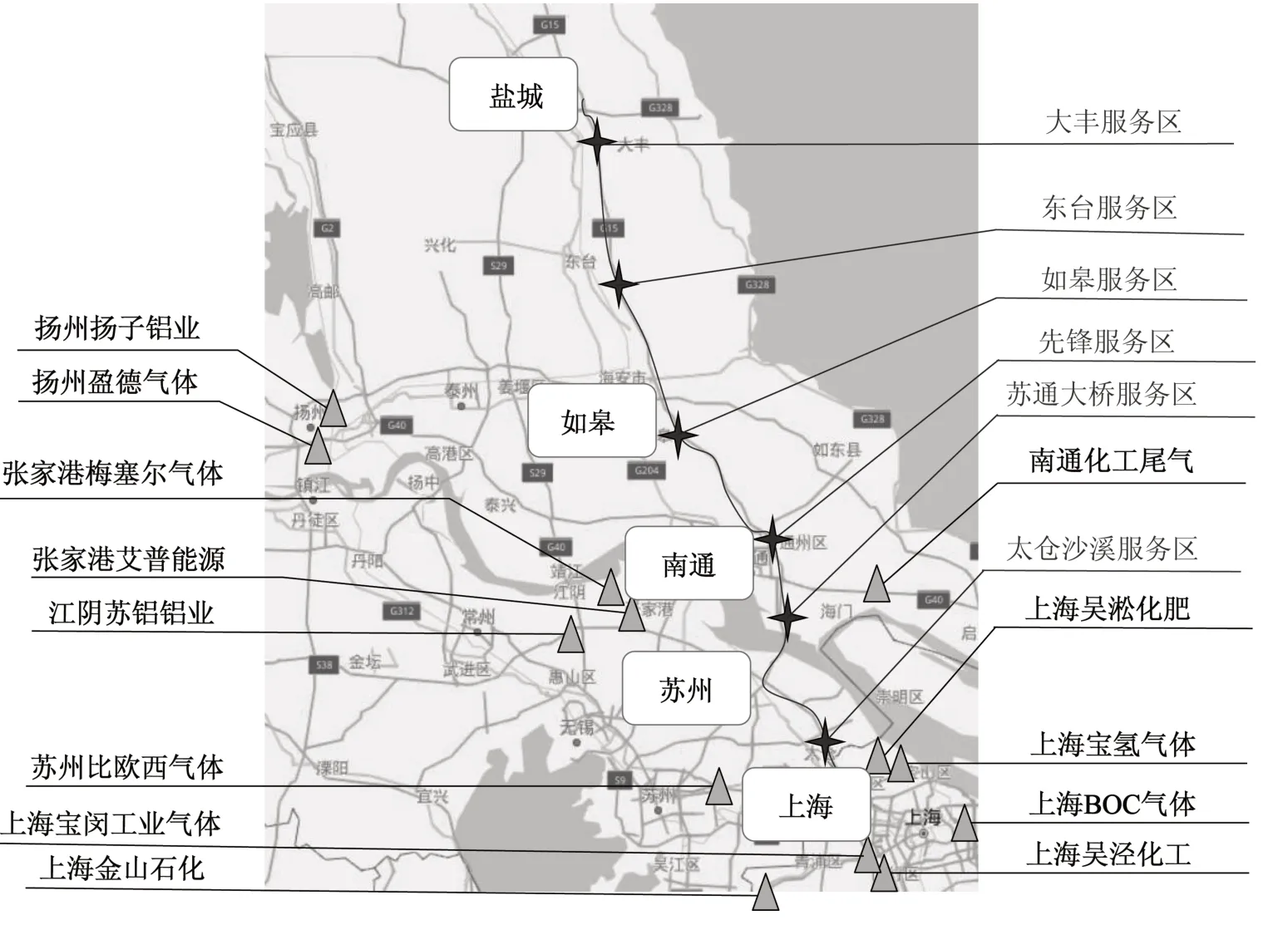
图2 热点城市、服务区、制氢厂分布Fig.2 Distribution of cities,service areas,and hydrogen sources

在式（20）中目标函数的权重选取方面，本文取w=100，v=1。确保在优化过程中，优先对初始投资Ccap，i最小化，然后再将运营成本Cope，i最小化。

2 实例计算与结果分析

2.1 计算结果

（1）鲁棒性方案，加氢站布点结果如表4所示。Cpir为2.572。

表4 鲁棒性方案下加氢站布点结果Tab.4 Results of locations of hydrogen refueling stations in robust scenario

（2）考虑随机性的经济性最优方案，加氢站布点结果如表5所示。Cpir为2.559。

2.2 结果分析

加氢站布点需要从整个加氢网络考虑，各个加氢站之间都会相互影响，局部最优并不一定能够达到整体最优。在G15高速公路上海—盐城段，共有6个候选地址，比如设置加氢站距离的最小最大限制，当限制相邻加氢站最大距离为100 km时，有效站点组合只有太仓沙溪—苏通大桥—如皋—东台服务区、太仓沙溪—先锋—如皋—东台服务区两个，若取消该约束，则还会增加太仓沙溪—苏通大桥—如皋—大丰服务区、太仓沙溪—先锋—如皋—大丰服务区两个站点组合。考虑到实际应用，对相邻加氢站的距离限制是有必要的。同样，考虑到技术条件、实际情况、法律标准等限制，也需要对加氢站加注能力进行限制，避免出现部分加氢站加注能力过大过小等现象，表4与表5中400 kg·d-1就是对加注能力下限的限制。

表5 考虑随机性时的加氢站布点结果Tab.5 Results of locations of hydrogen refueling stations considering uncertainty

类似地，在计算氢气购入方案时，也需要从整体上进行考虑，因为氢源的制氢能力是有限的，当用氢量很大时，每个加氢站都从离其最近的氢源购氢时，可能会超过氢源的产量，就需要从多个氢源购入氢气，在本例中，各氢源的氢气产量足够，故不需要从多个氢源购入氢气。此外，也需要权衡氢源氢气价格和运输成本，这就需要进行分析计算以达到整体最优。在本例中，因氢源价格一致，故只需优化运输距离。而在燃料电池汽车发展初期，各氢源的氢气产量足够，故每个加氢站都从离其最近的氢源购入氢气。当氢气需求上升，单个氢源不足以供给加氢站的氢气需求时，多氢源供氢的必要性就凸显了，表6给出了鲁棒性方案下，当氢源产量为原本的10%～70%时加氢站位置及站点加注能力的变化（为了说明氢源产量对加氢站位置的影响，该处不考虑相邻加氢站的距离限制）。

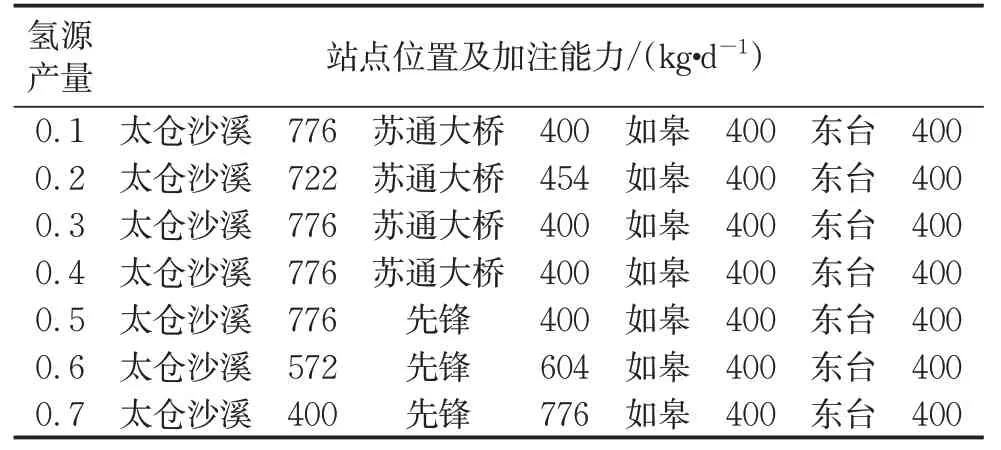
表6 不同氢源产量下加氢站的位置及站点加注能力Tab.6 Locations and capacity of stations with different capacities of hydrogen sources

当氢源产量达到0.7时，加氢站的位置和加注能力已经与原来的相一致，故无需继续计算。从表6中可以看到，当氢源产量从原来的0.4变成0.5时，加氢站的位置发生了变化。这两种情况下的氢气购入方案如表7和表8所示。

从表7和表8的对比中，可以看到，当氢源产量为原来的0.4时，苏通大桥加氢站的主要氢气来自张家港艾普能源，而当氢源产量为0.5时，由于南通化工尾气的氢气产量更加充足，也有更多氢气来自该处。对于张家港艾普能源来说，苏通大桥服务区更近，分别为65和80 km，而对于南通化工尾气来说，先锋服务区更近，分别为45和60 km，故氢气运输成本的最小化使加氢站位置发生了变化。类似的，各站点加注能力的变化也是由于根据成本进行优化的。从这里也可以看到，加氢站布点模型是一个整体，需要综合考虑多方面的要素影响。

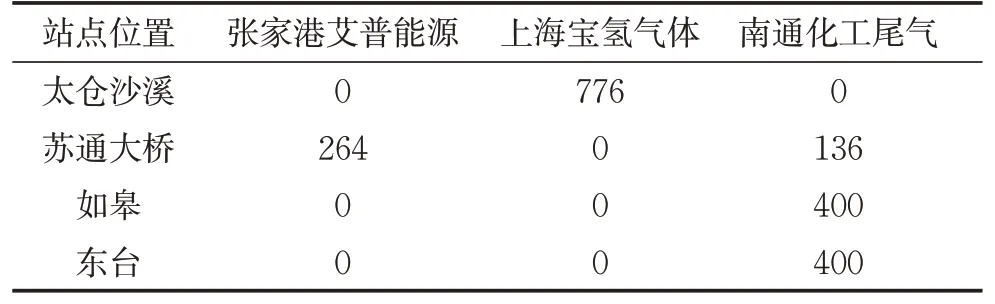
表7 氢源产量为原来的0.4时的氢气购入方案Tab.7 Hydrogen purchase scheme at a proportion of capacity of hydrogen source of 0.4 kg·d-1

表8 氢源产量为原来的0.5时的氢气购入方案Tab.8 Hydrogen purchase scheme at a proportion of capacity of hydrogen source of 0.5 kg·d-1

关于氢气需求的分配，即哪些用户去哪个加氢站加氢，也是加氢站布点的重要问题之一。本文中采用的分配方式是能使加氢站成本最小化的系统最优分配，包括满足氢气需求覆盖最大化和氢气购入成本最小化两个方面。氢气需求覆盖最大化是指将用户的氢气需求分配至各加氢站后，使得被满足的氢气需求最大。而氢气购入成本最小化则是当氢气需求可以被全部满足的情况下，可能存在多种分配方式，从中选出能使加氢站氢气购入成本最小化的一种。从方案结果中也可以看出，东台服务区的亏转盈年限比其他几个加氢站大得多，这是因为这个站点的氢气购入成本最大，由于随机性的存在，当全部加氢站的加注能力大于总氢气需求时，系统最优的分配方式会优先将需求分配到其他站点，因此该站点的平均收入较少。表9是鲁棒性方案下当各流动的氢气需求取最大值时的需求分配。

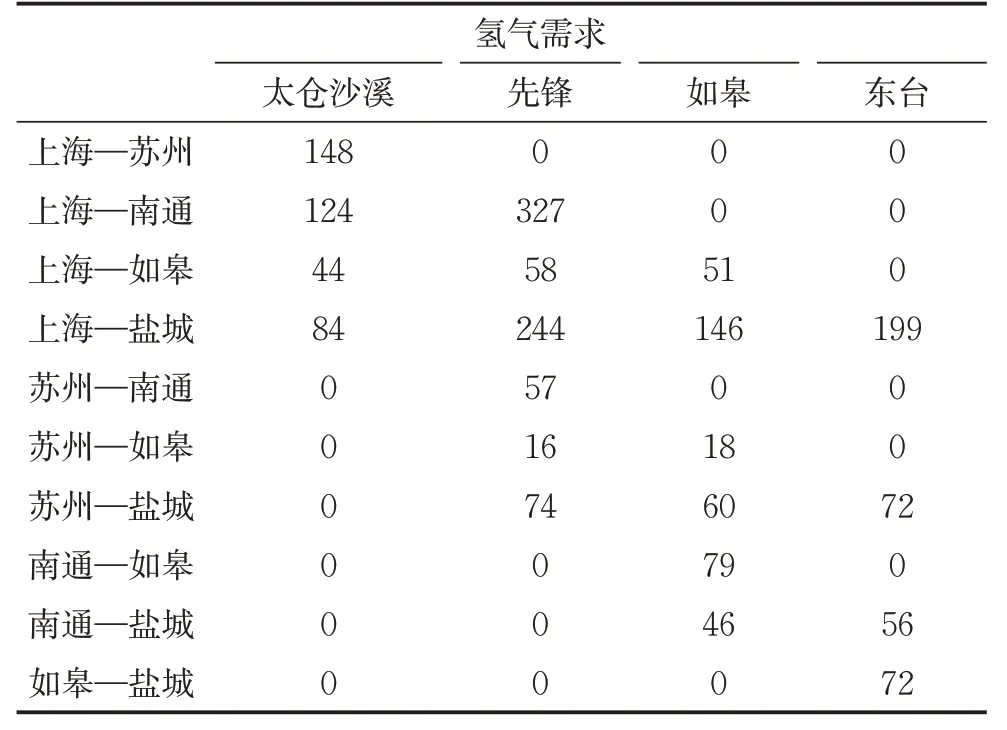
表9 鲁棒性方案下的氢气需求分配Tab.9 Distribution of hydrogen demand in the robust scenario kg·d-1

3 结语

本文通过建立快速路一维道路加氢站布点模型，通过指导在燃料电池汽车示范热点城市高速间进行加氢站科学布点，构建区域性的加氢站网络，不仅可以满足大部分燃料电池汽车用户的城际旅行的需求，还可以减少加氢站的建设成本，实现加氢站的高效利用。通过本文的研究，将加氢站建设和使用的经济性分析进行优化，综合相邻站点距离与数量限制、站点加注能力限制和流动的随机性等因素，建立快速路一维道路加氢站布点数学模型，并采用穷举法和线性规划以及粒子群算法求解。采用该模型，对G15上海—盐城段进行加氢站布点仿真计算，构建长三角地区加氢站网络。计算结果表明该模型在给定的限制条件下，得出合适的站点位置和加氢站加注能力，并给出每个加氢站的氢气购入计划。

作者贡献声明：

吕洪：确定论文研究内容和建模方法，指导论文撰写及修改。

郑乾辉：模型建立和数据处理，以及论文撰写。

周伟：建模协助指导。

张存满：选题协助指导。