桥梁施工线形无人机测量方法与参数优化

石雪飞，许 琪，马海英

（同济大学土木工程学院，上海 200092）

悬臂拼装法施工速度快、质量易控制，是最常用的大跨径桥梁施工方法。但在施工过程中必须对桥梁线形及受力状态进行测控，使结构实际线形与预期状态之间的误差在容许范围内，以保障拼装精度和成桥质量。大跨度桥梁悬臂施工的线形控制工作量大、精度要求高、难度大，同时施工控制误差的影响因素较多，自适应控制法通过在施工控制中引入参数识别，为主动进行结构施工状态的准确控制提供决策依据，可获得高质量的施工控制结果［1］。

自适应施工控制过程中，从反馈计算和参数识别的角度出发，希望每个工况内测量的节点数和次数越多越好，大大增加了测量的工作量［2］。采用全站仪或水准仪的传统测量方法耗费大量时间和人工，降低了施工速度，在工期紧张的时候，往往不能对所有安装节段进行全面测控，影响了施工质量。为了提高施工效率，保障施工质量，亟需研究不依赖人工的更高效的测量方法。

随着智能全站仪、电子水准仪、全球卫星导航系统（global navigation satellite system，GNSS）、激光扫描、摄影测量等测绘技术的发展，新兴桥梁线形测量方法得到了快速发展［3］。GNSS技术具有全天候、自动化、不受气候影响等优势，国内外部分特大跨径悬索桥和斜拉桥均安装了GNSS变形监测系统，对大桥主缆、桥面、桥塔三维振动位移的监测精度可达到1～2 cm［4-5］。但GNSS测量技术需在结构上设置固定观测站，在施工现场易损坏，且成本较高，难以布置很多监测点，无法满足自适应施工控制的多节点测量需求。

摄影测量技术通过量测相机摄取的二维图像，测定物体在三维空间的位置、形状、大小乃至物体的运动。近百年来，摄影测量经历了模拟、解析与数字摄影测量三个阶段［6］，如今数字摄影测量已在工业制造、地理测图、三维建模、工程测量等领域获得了广泛应用。Ohnishi等［7］采用近景摄影测量技术进行边坡的变形监测，唐君萍等［8］利用近景摄影测量技术对飞机复杂零件进行检测和尺寸测量，周颖等［9］将摄影测量和计算机视觉用于结构系统和混凝土裂缝的识别与测量，在实验室条件下精度均可达到0.1 mm。目前，用于机械零件尺寸测量和逆向工程的近景摄影测量精度已达到毫米级，但对测量条件要求较高，拍摄距离很近，不适用于桥梁施工现场的环境。

无人机（unmanned aerial vehicle，UAV）具有高机动性，可到达人类难以抵达的观测点，快速获取多视角数据，近年来无人机导航、障碍物检测与回避、空中决策等算法和计算机视觉技术发展迅速［10］，促进了其在自动监测、基础设施巡检、灾难响应、施工管理、测绘和结构三维重建等方面的应用［11］。He等［12］研究表明，借助全局光束平差算法，使用消费级无人机可达到厘米级的重构精度。要将无人机应用于施工控制测量，还需进一步提高精度水平，目前已有一些学者从设备、拍摄方案、算法等方面展开研究。Delgado等［13］采用全站仪建立辅助参考点，与无人机的惯性测量单元（IMU）数据融合，提高了图像配准精度，得到的桥梁点云模型可用于主梁变形测量。Morgenthal等［14］使用增强设计的无人机对不同桥梁构件进行了目视检查，研究了风等自然环境对机器视觉自动检测结构损伤的影响。Habib等［15］通过研究发现图像的相对定向直接影响点云的重建成功率和图像校正，对重建精度至关重要。Ellenberg等［16］研究了不同拍摄距离、运动和静止状态下无人机检测裂缝和位移的准确度和测量精度。刘春等［17］通过无人机摄影测量进行了单体异形建筑的三维重建，比较了环绕式摄影和传统倾斜摄影建模方法的效率和质量。Yoon等［18］在实验室中模拟钢桁架桥的垂直动态位移，通过无人机拍摄视频提取结构的实际位移，产生的均方根（root mean square，RMS）误差约2 mm。

综上所述，无人机摄影测量具有高机动性、低成本、不依赖人工等优势，将其应用于桥梁线形测量，可解决自适应施工控制过程中线形通测的难题。但对于桥梁施工线形测量这种尺度大、测点多、精度要求高的任务，目前还未有研究探索无人机测量的可行性、方法和精度水平。本文考虑桥梁施工测量的特点，提出桥梁线形无人机测量的技术框架和主要控制参数，研究适合施工现场的标记点布置方式与航线规划，并通过试验定量研究各控制参数对测量精度的影响，在此基础上建立无人机测量方案的优化方法。

1 桥梁线形无人机摄影测量方法

1.1 相机成像原理

摄影测量利用立体视觉原理进行三维重构，结合图像处理、射影几何和统计学方法，解析恢复不同角度图像上特征点的空间交会光线，并通过光束法平差求解特征点的三维坐标。相机成像是摄影测量的第一步，可分为4个步骤：刚体变换、透视投影、畸变校正和数字化图像，涉及到4个坐标系的变化：像素坐标系OUV、图像坐标系OpXpYp、相机坐标系OcXcYcZc、世界坐标系OwXwYwZw［19］。线性相机模型如图1所示，相机成像的总转换关系式见式（1）。

图1 线性相机模型Fig.1 Linear camera model

式中：（Xw，Yw，Zw）为相机坐标系中空间点的坐标；（u，v）为像素坐标系中像点的坐标；Zc表示空间点到相机坐标系原点距离；K为相机内参矩阵；（u0，v0）为像片中心点；dx和dy为单个像素在图像坐标系u轴和v轴方向的长度；f为相机焦距；R、t为相机坐标系变换到世界坐标系的旋转矩阵和平移向量。

1.2 摄影测量标记点坐标解算

摄影测量常在被测物表面设置专门测量标记点，由外围编码环段和中心圆点组成，编码环段用于计算机快速准确地识别，中心圆点用于坐标定位，如图2所示。桥梁施工现场环境复杂，摄影测量的条件与室内相比较为恶劣，在桥面上布设标记点可提供易识别的特征，提高重构成功率和测量精度。

图2 摄影测量标记点Fig.2 Photogrammetric markers

识别并匹配各图像中的标记点后，首先采用五点算法（five-point algorithm）求解基本矩阵，定向每张图像对应的相机位置，然后利用三角测量（triangulation）解算出各标记点的三维坐标［20］。根据立体视觉原理，通过两个不同角度的图像即可确定一点的三维坐标。假设空间中一点P，从两个角度拍摄图像，如图3所示。左侧相机坐标系OXcYcZc和世界坐标系OXwYwZw完全重合，图像坐标系为O1x1y1；右侧相机坐标系为OXrYrZr，图像坐标系为O2x2y2，相机焦距为f，将空间点在左右两图像中对应的像点称为像点1、像点2。

图3 根据双目视觉原理计算空间中一点坐标Fig.3 Calculation of the coordinates of a point according to the principle of binocular vision

根据相机成像模型，可计算出空间点的三维坐标如下：

式中：（x1，y1）和（x2，y2）为像点1、像点2在图像坐标系O1x1y1和O2x2y2中的坐标；（u，v）为像点1在其像素坐标系中的坐标；dx、dy为单位像素在像素坐标系u轴、v轴方向的长度；Zc为空间点到相机光轴中心的距离；f为相机焦距；r1，r2，…，r9为两个相机坐标系变换矩阵的元素。

为了提高测量精度，通常需要更多角度的图像进行迭代计算以减小误差，如式（5）。对每个标记点进行三角测量和迭代计算，得到其在世界坐标系中的三维坐标，属于局部意义上的求解优化，在实际测量过程中，还需对所有测点进行整体误差优化。光束法平差［21］可在全局意义上缩小各图像上真实像素点和重投影像素点之间的误差，最小化重投影误差可按式（6）进行计算，需要进行多次迭代求解。

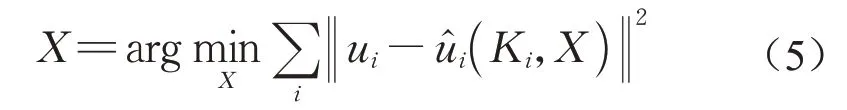
式中：X为满足条件的空间点最优三维坐标；ui为该点在第i幅图像上的像点坐标；(Ki，X)为推算出的X投影到图像上的重投影像点坐标。

式中：ε为重投影误差的最小值；n为空间点的个数；m为相机位置的个数；Q（bi）为预测的第i个点；xij为第j张图像上的第i个特征点；d（x，y）表示图像上由不同向量x和y表示的点的欧式距离。

根据摄影测量原理，飞行高度H、投射线夹角θ、视角数量、照片数量等控制参数对精度有较大影响。由式（2）—（4）可知，测点坐标是单个像素在像素坐标系中轴向长度dx、dy和拍摄距离Zc的函数，当相机参数一定时，dx、dy与拍摄距离正相关，飞行高度对测量精度有直接影响。采用光束法平差优化整体测量误差时，投射线夹角越小，坐标解算的偏差范围越大，即可能的误差越大，如图4所示，要获得较好的平差效果，投射线夹角不能过小，同时由式（6）可知，相机视角数量越多，光束法平差的结果越接近点的真实位置。并且，无人机悬停拍照时的振动会降低图像质量，进一步影响测量精度，通过拍摄多张重复照片可提高测量冗余度，降低振动的影响。

图4 不同投射线夹角与点定位精度关系Fig.4 Relationship between angle of bundle and point positioning accuracy

1.3 测点标高计算

摄影测量得到的是局部测量坐标系下的测点坐标，需引入基准点进行刚性坐标变换，将其换算到同一桥梁坐标系中，得到测点的实际标高，才能用于施工控制。坐标系转换可采用间接平差方法［22］，提供三个已知点坐标，即可完成转换求解，得到桥梁坐标系下测点的实际标高，坐标系转换求解过程见图5，图中R，t分别为两坐标系之间的旋转矩阵和平移向量。对于悬臂施工桥梁，基准点可设置在桥塔、桥墩根部等位置，并经常进行校准。

图5 引入基准点进行测点坐标系转换Fig.5 Introducetion of datum point in transformation of the coordinate system of measuring point

1.4 桥梁线形无人机测量方法框架

将无人机应用于桥梁悬臂施工控制测量，首先需根据结构特点设计标记点布置方案，然后综合考虑测量精度和效率，确定飞行高度H、投射线夹角θ、视角数量、照片数量等控制参数，并规划无人机航线。执行无人机测量任务得到图像数据，通过畸变校正、标记点识别和三维坐标求解得到各标记点的坐标，最后关联基准点进行坐标转换，得到各测点在桥梁坐标系下的真实标高，方法框架见图6。

图6 桥梁线形无人机摄影测量方法框架图Fig.6 Framework of bridge alignment UAV photogrammetry method

2 标记点布置方式与航线规划

2.1 标记点布置方式

室内摄影测量标记点主要用于设置比例尺或辅助识别被测物轮廓，多密集布置在测区角点、边缘等位置。但测量主梁节段的标高和线形，标记点宜布置在节段表面中轴线和翼缘根部，且布置过密会影响测量便利性，需根据主梁节段的尺度研究合理的标记点布置方式。

针对桥梁施工线形测量的特点，设计了几种标记点布置方案，见图7，标记点布设为3列，两侧为测点，中间为辅助加密点。方案一、方案二用于比较加密点对测量结果的影响，方案三、方案四用于比较测量标记点间距的影响，4个方案标记点横向间距均为1 m。

图7 标记点布置方案Fig.7 Layout plan of marking points

方案一、二、三均可成功解算出标记点坐标，方案四由于标记点间距过大、数量太少，解算失败。由表1可知，辅助加密点对计算精度影响很小，测量点间距越小精度越高，当测量点间距为1.5 m时，能保证重建成功率和较高的精度，同时可减少标记点数量，提高测量效率。

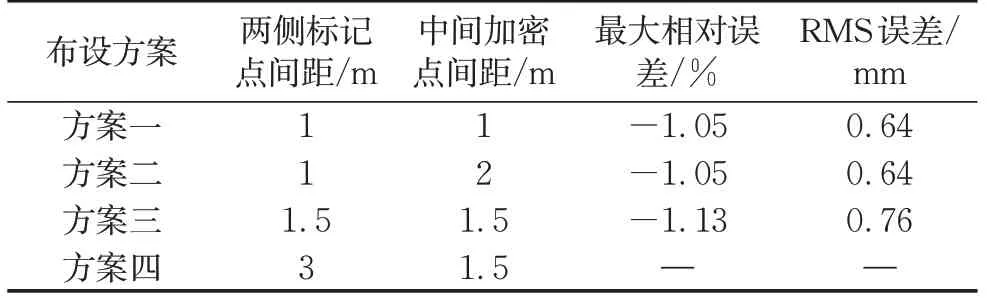
表1 各标记点布置方案及测量结果Tab.1 Layout plan and measurement results of each marking point

2.2 航线规划

预设航线可提高测量效率，对于直线型桥梁，将测区简化为矩形，无人机需到达图中所有预设拍摄位置，效率较高的航线包括巡回航线和S形航线，如图8、图9所示。

图8 巡回航线Fig.8 Itinerant route of UAV

图9 S形航线Fig.9 S-shaped route of UAV

从航线长度、转弯次数、镜头旋转次数、飞行时间等方面比较两种航线效果，见表2。巡回航线长度更长，但转弯次数和镜头旋转次数远少于S形航线，总飞行时间更短，可节省25%的电量。因此，巡回航线更适合桥梁施工线形测量需求，但需在桥面上方预留足够的飞行空间。直线形梁桥、上承式拱桥可采用本节所述方法布置标记点和规划航线，斜拉桥和悬索桥则需要考虑拉索、主缆、吊杆的位置，适当地将标记点布置在桥面中心位置，两侧为无人机留出3 m以上的避障空间。

表2 两种航线效果比较（测量长度为45 m）Tab.2 Comparison of two flight routes(at a measured length of 45 m)

3 测量控制参数试验分析

3.1 试验设计与测量结果

根据无人机摄影测量原理，飞行高度H、投射线夹角θ、视角数量、照片数量是精度的主要控制参数，为定量分析各控制参数的影响，开展了一系列对照试验。在地面上布置一组标记点，如图10所示，试验过程中，无人机相机参数保持不变，焦距为10.24 mm，光圈为f/4.5，快门速度为1/120 s，IOS为100。采用无人机测量各点坐标，并计算两点间距，使用卷尺多次测量标记点间距取平均值作为真值，以最大相对误差和RMS误差表征测量精度，部分试验结果见表3。

表3 不同控制参数下的试验结果Tab.3 Experimental results with different control parameters

图10 标记点排列方式Fig.10 Layout plan of marking points in the experiment

3.2 无人机飞行高度的影响分析

控制飞行高度在2.7～7.7 m范围内，分别选择8个视角和4个视角，令无人机在各位置悬停拍摄4张照片，各飞行高度下的测量精度见图11。随着飞行高度增加，最大相对误差和RMS误差均逐渐增大，当高度不超过5 m时，最大测量误差不超过1 mm，RMS误差为0.4 mm，误差基本稳定，当高度增加到8 m左右时，RMS误差增大到1.5 mm左右，最大测量误差超过2 mm。

图11 无人机飞行高度对精度的影响Fig.11 Influence of UAV flight height on accuracy

通过试验发现，无人机摄影测量的精度水平与单位像素真实尺度Zcdx、Zcdy大致相当，当相机分辨率、传感器等参数固定时，精度水平直接与飞行高度相关。对于本试验所用的无人机，要将最大误差控制在1 mm以内，建议的飞行高度为5 m。可以通过提高相机分辨率、传感器画幅尺寸等方式进一步提高适用的飞行高度，拓展应用空间。

3.3 投射线夹角的影响分析

两次拍摄相机镜头中心点与物点连线的夹角被称为投射线夹角，如图12中的θ角，通过改变无人机云台倾角γ，可调整投射线夹角的大小。投射线夹角与平差效果密切相关，通过试验定量研究无人机摄影测量精度与投射线夹角之间的关系。

图12 投射线夹角与云台倾角的关系Fig.12 Relationship between angle of bundle and camera inclination

控制投射线夹角从10°增大到120°，测量精度的变化见图13。当θ＜40°时，部分图像定向失败，当θ＞110°时，部分标记点识别失败，测量误差均较大；当40°≤θ≤110°时，标记点识别和图像定向成功率都较高，误差可控制在0.6 mm以下。因此，要达到较高的测量精度，需控制投射线夹角区间为40°～110°，对应的云台倾角为35°～70°。

图13 摄影测量误差与投射线夹角关系Fig.13 Relationship between photogrammetry error and angle of bundle

3.4 视角数量的影响分析

相机视角数量越多，光束法平差的结果越接近点的真实位置，精度越好。但是减少相机视角数量可提高拍摄效率，且平行或垂直于测量轴线方向的视角更便于无人机规划航线自动拍摄。在同一拍摄高度，保证投射线夹角处于高精度区间，分别采用2～8个相机视角进行拍摄，如图14所示。

图14 不同相机视角拍摄方案Fig.14 Different camera position schemes

各视角选择4张照片进行重建，不同方案的测量精度见图15。只有2个视角时，没有多余角度的图像用于平差，精度较差且不稳定。随着视角数量增多，测量精度逐渐提高，但当增加到4个视角之后，提高的幅度较小。综合考虑精度和拍摄便利性，4个相机视角的方案最优。

图15 不同视角数量对精度的影响Fig.15 Influence of different number of viewing angles on accuracy

3.5 照片数量的影响分析

通过拍摄多张重复照片可提高测量冗余度，降低无人机悬停振动的影响。控制飞行高度不变，选择8个视角和4个视角，各位置分别选择1～5张重复照片进行重建，测量精度见图16。

图16 照片数量对精度的影响Fig.16 Influence of photo quantity on accuracy

各位置只有1张照片时，所选照片质量对结果的影响非常大，标记点识别成功率低，测量误差较大。当照片数量为2张以上时，重建成功率大大提高，最大相对误差也降低到0.10%以内，RMS误差可控制在0.6 mm以内。当照片数量达到3张后，继续增加照片对精度的影响很小。另外，约3～4 s可完成一张照片的标记点识别、定向和坐标解算，总计算时长和照片数量成正相关，对于4个视角数量方案，取3张照片时，30 s左右可完成坐标解算。

4 无人机测量控制参数实用优化方法

4.1 飞行高度

无人机进行线形测量任务时，主要控制参数包括飞行高度、投射线夹角（云台倾角）、相机位置和照片数量。根据第3节的研究，无人机摄影测量的精度水平和单位像素真实尺度大致相当，已知相机参数和测量精度要求时，可根据相机成像原理反推出可行的飞行高度区间。

完成相机标定后，图像分辨率和镜头标定区域占比均为已知，假设镜头焦距为f，mm，图像分辨率为I1×I2（单位：像素），传感器尺寸为W×H（单位：mm），镜头标定区域占比为c，见图17。

图17 无人机飞行高度确定原理示意图Fig.17 Key parameters of UAV measurement scheme

假设待测视域为一a×b（单位：m）的矩形，考虑镜头标定区域占比，相机需要达到的视域范围为（a×b）/c，故飞行高度h需满足式（7）：

根据线性相机模型，飞行高度h和单位像素真实尺度Zcdx、Zcdy的关系见式（8）、式（9）。试验表明，控制Zcdx=Zcdy=1.2 mm可令无人机测量精度达到毫米级，此时飞行高度h应满足式（10）。

4.2 相机云台倾角

改变无人机相机云台倾角可调整投射线夹角和投射线倾角（图18）。要保证投射线夹角位于高精度区间，需控制云台倾角范围为35°～70°。较小的云台倾角可提供更大的视野范围，也可提高各标记点的投射线夹角，但标记点中心圆点成像后通常为椭圆，倾角越小变形程度越大，会降低识别鲁棒性。大量试验表明当投射线倾角大于30°时，标记点识别有较高的成功率［23］，此时云台倾角γ需满足式（11）。

图18 云台倾角与投射线倾角的关系Fig.18 Relationship between camera inclination angle and bundle inclination

4.3 相机位置及照片数量

增加相机位置可提高测量精度，但当增加到4个相机位置之后，提高的幅度较小。综合考虑测量效率、计算时长和无人机航线规划便利性，选择4个不同相机位置采集照片。

为缓解无人机悬停振动对成像质量的影响，保证重建冗余度和测量精度，可在各相机位置采集3张重复照片。

4.4 模型试验验证

为验证本节所述优化方法的有效性，选择了一段28.5 m的跑道进行了模型试验。测量标记点布置方案如图19所示，设置8个已知坐标的控制点作为基准点和校准点。控制无人机飞行高度为5 m，云台倾角为60°，采用巡回航线从4个不同视角采集照片，各位置采集3张重复照片。将摄影测量得到的各测点标高与全站仪测得的标高比较，各点测量误差如图20所示，采用优化后的摄影测量方案，可将误差控制在2 mm以内。

图19 模型试验标记点布置方案（单位：mm）Fig.19 Layout plan of marking points for model experiment(unit:mm)

图20 各测点标高测量误差Fig.20 Elevation measurement error of each marking point

5 结论

本文考虑桥梁施工控制测量的特点和无人机摄影测量原理，提出了桥梁线形无人机测量的技术框架和测量控制参数。主要研究结论包括：

（1）在桥面上布设标记点可提高重构成功率和测量精度，标记点宜布置在节段中轴线和翼缘根部，测点间距可设置为1.5 m。对于直线桥梁，巡回航线耗时短、耗电量低、效率高，可实现自动化测量。

（2）无人机进行桥梁施工线形测量需控制的技术参数包括飞行高度H、投射线夹角θ、视角数量、照片数量等。飞行高度对测量精度有直接影响，对于本无人机，高度不超过5 m时，精度可控制在1 mm以内；投射线夹角与平差效果密切相关，当40°≤θ≤110°时，标记点识别和图像定向成功率都较高；4个视角数量可得到较好的测量精度，也便于无人机航线规划；采集3张重复照片，可保证冗余度和计算速度。

（3）建立了桥梁悬臂施工线形无人机测量控制参数优化方法，无人机摄影测量的精度水平和单位像素真实尺度Zcdx、Zcdy大致相当，已知相机参数和精度要求，可根据成像原理反推出可行的飞行高度区间。确定相机云台最优倾角范围需综合考虑投射线夹角和倾角的要求，控制光束平差和标记点识别精度较高。采用优化后的摄影测量方案进行了模型试验，可将误差控制在2 mm以内。

作者贡献声明：

石雪飞：研究理念、研究方法、论文撰写。

许琪：研究方法、数据建模与分析、试验与分析、论文撰写。

马海英：研究理念、数据建模与分析、论文撰写。