大跨公轨合建斜拉桥主-引桥地震相对位移响应与控制

管仲国，徐瑜窈，郑志均

（1.同济大学土木工程学院，上海 200092；2.杭州市城建设计研究院有限公司，浙江杭州 310001）

在国内外的抗震设计实践中，大跨度斜拉桥较多采用两级设防标准：功能性设防标准对应的地震重现期一般为100～475年，震后结构应满足全部正常服役性能目标；安全性设防标准对应地震重现期一般为1 000～2 500年，震后应满足有限损伤、可修复的性能要求。通常情况下，主桥和引桥由于结构形式不同，动力特性差异也较为显著，因此在地震作用下极易发生主-引桥较大的相对位移，由此引发的实桥结构震害也非常多见［1］。公路桥梁对这一问题一般通过增加过渡墩处的支承长度来解决，但这仅是一种防落梁的构造措施。对于公轨合建桥梁，为保障轨道行车的连续性，梁间伸缩缝的相对位移不得超过接轨器的最大变形能力，否则就会破坏轨道系统，导致通行功能中断。

斜拉桥的地震响应在很大程度上与结构抗震设计方案息息相关［2］。一般而言，采用漂浮体系可以显著延长结构的纵向振动周期［3］，进而显著改善斜拉桥结构的纵向抗震性能。当斜拉桥的下墩塔柱足够高时，其自身较大的柔度也可以延长结构周期，降低结构地震响应［4］。李立峰等［5］指出超高墩多塔斜拉桥采用固结体系和弹性-固结体系，可在不显著增大结构地震内力的同时大幅降低结构变形。此外，由于大跨度桥梁自身的阻尼特性一般比较低，常通过附加阻尼控制其位移响应［6］。Zhu等［7］采用附加粘滞阻尼器控制某大跨斜拉桥在地震作用下的主梁纵向位移；Xie等［8］则研究了不同阻尼器布置方案的减震效果。

对于相邻结构在地震下的相对位移，一般认为主要是由于结构固有周期的差异导致的［9］。陈逸民等［10］研究了相邻联周期比对桥梁地震反应的影响规律；罗致［11］基于相邻联周期比，探讨了山区高墩连续刚构桥的合理设计策略；美国加州地震设计规范［12］为减小非同向振动的影响，建议相邻联桥的周期比不小于0.7。Hong［13］、Wang［14］等的研究显示，考虑地震作用的非稳态过程，相邻结构的阻尼特性差异同样会导致显著的相对位移响应，进而基于自振频率比和阻尼比两参数建立了估计相邻结构防碰撞临界间距的方法。对于地震下相邻结构相对位移的控制研究，吕西林等［15］分析了高层结构与低矮裙房的地震相对运动，并采用在接缝处设置粘滞阻尼器的方法来减小其相对位移响应，朱宏平等［16］基于相邻单自由度结构推导了在相邻结构间附加粘滞阻尼器控制其相对位移的理论方法，沈文爱等［17］指出在双座串联大跨度斜拉桥间设置粘滞阻尼器，对于减小两桥的相向运动具有很高的控制效率，Bhaskararao等［18］推导了以粘滞阻尼器连接的两个单自由度相邻结构的运动控制方程，指出粘滞阻尼器的最优阻尼是关于质量以及相邻结构频率比的方程。这种控制方法实质上就是利用结构间的相互运动来消耗和吸收振动能量，或者减轻单个结构的振动响应、或者强化相邻结构运动的同步性来达到降低相对位移的目的。对于大跨度桥梁的主、引桥，一方面主、引桥结构的巨大差异很容易导致其固有周期的显著差异，但同时桥梁结构的周期又与其约束体系设计有很大的关系，可以通过改变其约束形式或引入适当的减隔震设计来显著改变结构的固有周期，另一方面主、引桥的阻尼特性一般也存在显著的差异，但同时也通过附加减震耗能措施进行调整。由此可见，大跨度桥梁的主、引桥地震相对位移的影响要素更加复杂，相应的控制手段选择也存在更多的可能性。

本文基于巴拿马运河四桥，开展大跨公轨合建斜拉桥的主-引桥的相对位移影响要素和控制研究。巴拿马运河四桥横跨巴拿马运河连接巴拿马城与泛美公路，为混凝土主梁斜拉桥，引桥为多跨连续梁，其中主桥和西岸引桥主梁为公轨共用。由于桥址场地地震风险很高，为确保轨道交通在功能性设防地震下能保持其正常服役性能，需限制主-引桥间的相对位移不超过接轨器的最大变形能力。

1 桥梁概况与分析模型

1.1 桥梁概况

巴拿马运河四桥主桥为双塔双索面斜拉桥，主跨510 m，立面布置如图1所示。主梁断面布置中间为地铁双线轨道，两侧为双向六车道公路，梁宽51 m，采用混合梁方案，其中钢混结合分界面位于中跨距塔身中心线16 m处，主梁断面如图2所示。斜拉索采用空间双索面呈扇形布置，主塔两侧各分布18对拉索，全桥共72对斜拉索；主跨拉索锚固间距为13 m，边跨拉索锚固间距为10 m；拉索采用平行预应力筋，由七股钢绞线组成压紧束，紧密排列成正六边形，包裹在圆形截面的抗紫外线高密度聚乙烯（HDPE）护套中。主塔为花苞形，总高度约为200 m，下塔柱高度75 m，为典型高墩大跨斜拉桥。每侧边跨设三个辅助墩和一个过渡墩，均为钢筋混凝土Y形空心墩，保证主桥整体景观一致，墩底顺桥向尺寸为5.9～6.8 m、横桥向为12.3～13.4 m。西侧主塔和桥墩基础采用桩基础，东侧主塔和桥墩则采用扩大基础。

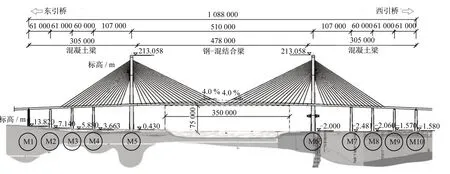
图1 主桥结构总立面图（单位：mm）Fig.1 Overall elevation of main bridge(unit:mm)

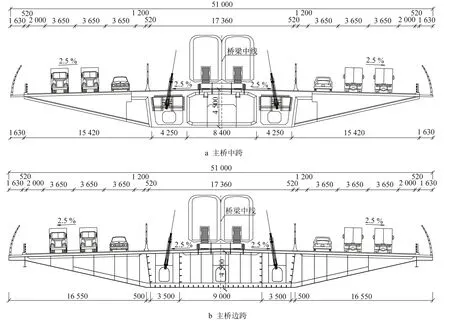
图2 主桥主梁断面图（单位：mm）Fig.2 Section of main bridge-deck girder(unit:mm)

东、西引桥均为混凝土连续梁桥。由于巴拿马桥址场地靠近赤道，温差较小，适宜采用多跨长联方案。西引桥跨径布置为6×60.5+5×61=668 m，桥墩为现浇钢筋混凝土Y形空心墩；上部结构为等高度箱梁，梁高4.5 m，宽51 m，同样为公轨合建模式。东引桥采用左、中、右分幅形式，中间幅为独立轨道梁（远期建设），左右幅均为公路桥，上部结构为等高度混凝土梁，桥墩采用Y型空心墩。

巴拿马四桥桥址场地属于高烈度地带，结构抗震问题较为突出，功能性设防和安全性设防标准分别对应地震重现期475年和2 475年。结构抗震性能目标：在功能性设防地震作用下的结构则应满足正常服役性能要求；在安全性设防地震作用下仅发生轻微-可修复损伤。本桥主桥与西引桥由于采用公轨合建模式，为确保轨道交通的正常运行，要求在功能性设防地震作用下主-西引桥之间的相对位移不应超出接轨器的变形能力±300 mm。场地地震安评对于每级地震设防水准提供了三组的模拟地震波，每组包含纵桥向、横桥向和竖向三个分量，地震反应分析的结果取三组波的响应最大值。总体上，三组波的结构响应幅值和规律均相差不大，图3所示为功能性设防水准下的导致结构相对位移响应最大的那一组场地安评地震波和相应的加速度反应谱，其中图3a中纵桥向、横桥向和竖向三个分量地震波峰值加速度（PGA）分别为0.240 1g、0.212 6g、0.294 3g。为简化起见，本文以下仅给出该地震波的结果。

图3 地震波及反应谱Fig.3 Seismic waves and response spectrum

1.2 分析模型

采用SAP2000软件建立了结构分析模型（图4），包括主桥和东、西相邻联引桥。其中主梁、主塔、桥墩采用空间梁柱单元进行模拟，拉索采用桁架单元，承台模拟为质点，东侧的主塔和过渡墩、辅助墩均为扩大基础，采用弹性土弹簧考虑基础柔度的影响，西侧主塔、过渡墩、辅助墩为群桩基础，在承台中部及底部采用p-y非线性土弹簧分别模拟承台、桩基与土的相互作用（p为桩侧土抗推力，y为桩基侧向位移）。其中承台底的集中p-y土弹簧为各墩塔通过pushover分析得到的群桩基础相对承台底的非线性力-位移关系，以此等效群桩基础的桩-土弹簧。以M7为例，在图5中给出了单桩典型深度处土弹簧py曲线及模型中承台中心和底部处土弹簧p-y曲线。

图4 全桥有限元分析模型Fig.4 Finite element analysis model of the whole bridge

图5 M7墩底p-y土弹簧曲线Fig.5 Curves of p-y soil spring at M7

为计算主-引桥相对位移，同时考虑边界联的影响，模型还包含了东、西引桥部分，采用与主桥相类似的原则进行建模。东、西引桥采用摩擦摆支座进行减隔震设计，采用Friction Isolator单元模拟，其中摩擦系数的取值为0.01～0.05。主桥中跨主梁钢材的弹性模量E=200 GPa，主、引桥其他塔、梁、墩结构均采用混凝土，其材料特性如表1所示。另外，模型中用于减震的附加粘滞阻尼器采用Maxwell模型进行模拟。

表1 单元材料特性Tab.1 Constraints of each aseismic design

2 抗震设计方案及地震响应分析

2.1 抗震设计方案

巴拿马运河四桥为典型高墩斜拉桥，下部结构具有较大的柔度，能够较好地避开地震卓越能量频段并提供强震作用下的变形需要，此外桥址场地温度效应较小，因此在结构设计方案上可以有更多的选择。为优选巴拿马四桥的合理抗震设计方案，本文将对比漂浮设计方案、固结设计方案和仅塔梁固结设计方案三种抗震设计方案的结构地震响应。其中，漂浮设计方案的主梁与主塔、辅助墩和过渡墩之间容许自由地纵向滑动，横桥向为固定约束；固结设计方案主梁与主塔、塔墩、辅助墩完全固结，主梁与过渡墩容许自由地纵向滑动、横桥向为固定约束；仅塔梁固结设计方案中，仅主梁和主塔、塔墩之间采用完全固结，主梁与辅助墩、过渡墩之间容许自由地纵向滑动，横桥向为固定约束。这三种方案在静力条件下已被证明是可行的。

主桥与西引桥在主梁交接处共用过渡墩M10，墩上约束情况如图6所示，主梁与过渡墩间均采用纵向滑动支座，横向共用限位挡块，梁上钢轨采用接轨器连接。

图6 主、西引桥交接处约束图Fig.6 Junction of the main and west approach bridges

2.2 动力特性分析

表2所示为主桥在漂浮设计方案、仅塔梁固结设计方案和固结设计方案主桥、以及西引桥的首阶纵向振型特性描述，图7为相应的振型。可以看出，主桥在三种设计方案下的纵向自振周期存在较大的差异，漂浮设计方案结构柔度最大，其纵向自振周期远大于西引桥；固结设计方案刚度最大，其纵向首阶振型周期相较西引桥更短；仅塔梁固结设计方案的刚度介于漂浮设计方案和固结设计方案之间，纵向首阶自振周期与西引桥差异最小。

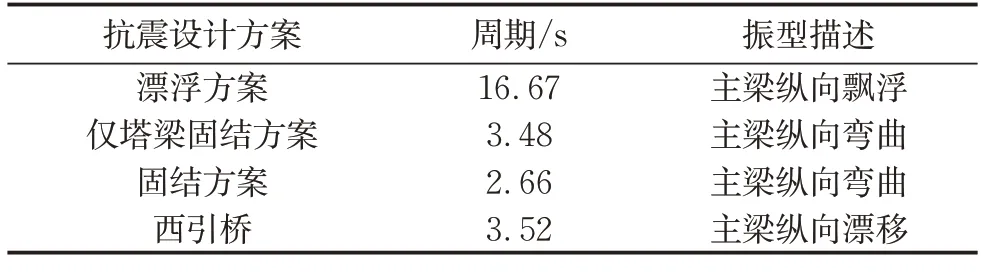
表2 各抗震设计方案主引桥首阶纵向振型Tab.2 First longitudinal mode of the main and approach bridges

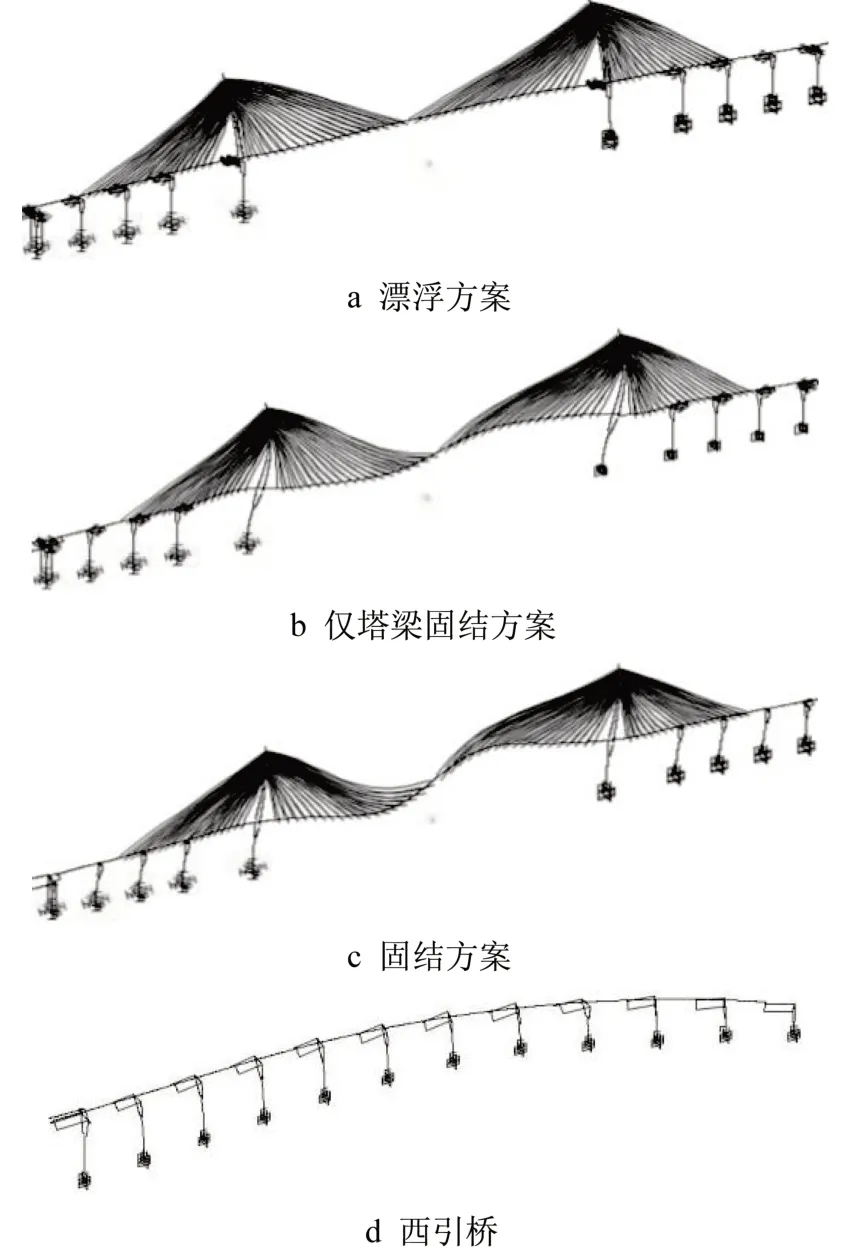
图7 主桥与西引桥首阶纵向振型Fig.7 First longitudinal mode of the main and approach bridges

2.3 墩、塔底内力分析

表3为各抗震设计方案在安全性地震作用下的墩、塔底纵、横桥向最大地震弯矩响应和抗弯能力对比情况。可以看出，尽管不同方案的约束方式对主塔塔底的纵向地震弯矩存在一定影响，但所有设计方案的塔、墩在纵、横向地震作用下的抗弯能力均大于地震需求。这表明任何一种设计方案均可满足安全性设防地震下的性能目标，由此可见，巴拿马运河四桥的主-引桥相对位移将成为结构抗震设计的关键问题。

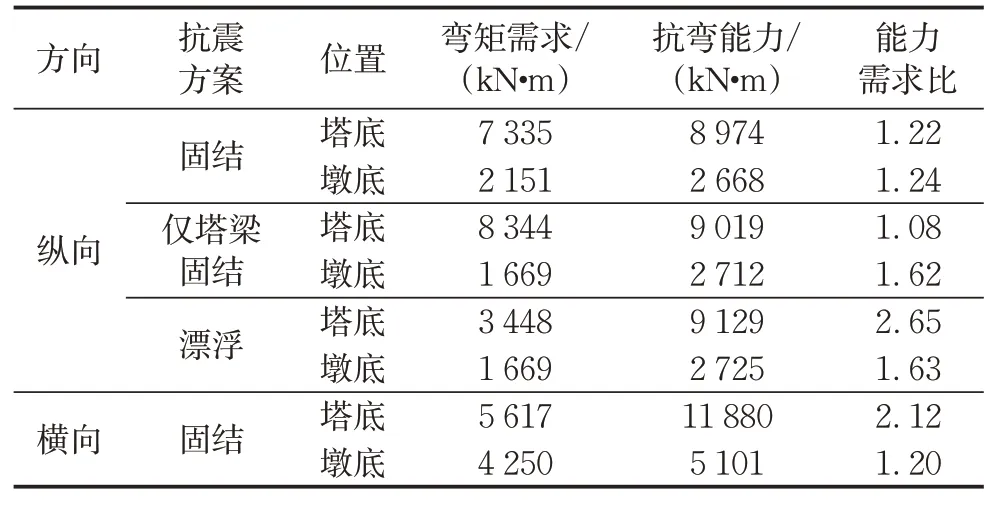
表3 塔、墩底地震弯矩需求与能力Tab.3 Demand and capacity of base bending moment of towers and piers

2.4 主-西引桥相对位移分析

图8a、8b和8c分别为固结方案、仅塔梁固结方案和漂浮方案的主桥-西引桥梁端位移与相对位移时程。图中三种抗震设计方案的主、引桥纵向振动频率差异程度并不相同。固结方案主桥梁端位移振动频率显著高于引桥，而漂浮方案中主桥纵向振动频率相较引桥更低，故固结方案和漂浮方案由于主引桥梁端纵向振动同步性差导致了较大的主引桥梁端相对位移，分别达到了0.22和0.20 m。对于仅塔梁固结方案，尽管其与引桥纵向振动周期相近，但主-引桥梁端相对位移也达到了0.19 m，究其原因，主要是主桥的梁端振动衰减较慢而引桥衰减较快所致。由此可见，相邻结构的相对位移响应不仅受周期差异的影响，而且还有阻尼差异的影响。

图8 主、引桥梁端位移时程Fig.8 Displacement time history of the main and approach bridges

巴拿马四桥要求在功能性设防地震下主-引桥梁端相对位移小于接轨器的最大变形量±300 mm，扣除车辆、温度等作用的影响，仅在地震作用的主-引桥梁端相对变形不应超过±180 mm，因此三种抗震设计方案的主-引桥相对变形均无法满足设计要求。

3 主-引桥相对位移影响分析

为进一步探究相邻结构的相对位移对周期和阻尼差异的敏感性，构建两个相邻的单自由度质量-弹簧-阻尼振子，如图9a所示，其中两个振子的阻尼机制均为粘滞阻尼；考虑到巴拿马四桥主桥首选附加阻尼为速度依赖型的粘滞阻尼器，而引桥采用的是位移依赖型的摩擦摆支座，为此进一步构建图9b所示的两个相邻单自由度振子，第①振子同图9a中的振子，第②振子则为质量-摩擦摆支座-弹簧系统，系统的刚度为弹簧刚度和摩擦摆支座等效刚度的串联结果，阻尼为摩擦摆支座耗能的等效系统阻尼比：

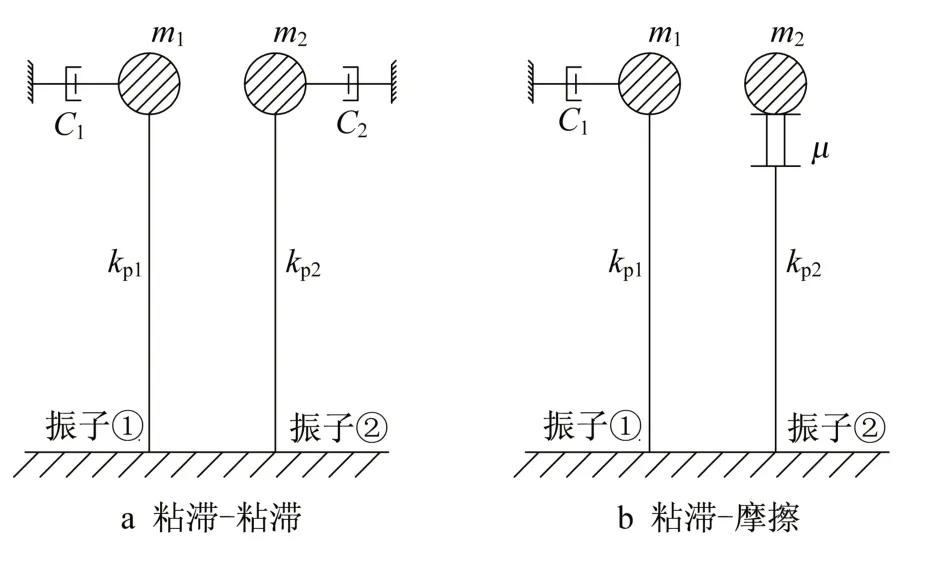
图9 单自由度模型Fig.9 Single degree of freedom model

式中：ξp为杆单元的阻尼比，取0.05；kp为杆单元的纵向刚度；ξeff为摩擦摆支座的等效阻尼比。ξeff为

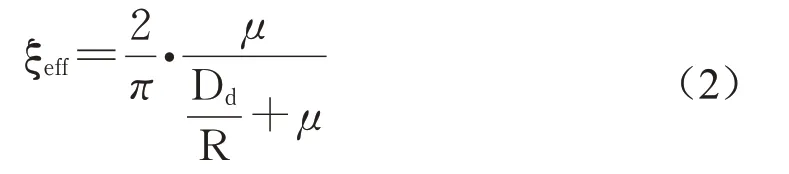
式中：Dd为摩擦摆支座在设防地震下的最大地震位移；R为滑动曲面的曲率半径；μ为摩擦摆支座的动摩擦系数。

调整振子①和②的周期分别等于巴拿马四桥主桥和引桥的首阶纵向振型周期，考虑不同的阻尼特性，计算得到两组振子在设计地震动作用下的相对位移，并表征为两个振子的周期比T1/T2和阻尼比之比ξ1/ξ2的变化曲线，如图10所示。其中，周期比为5.48和0.58，分别对应主桥为漂浮抗震设计方案和固结方案的工况，周期比为0.75、1、1.15则对应主桥为仅塔梁固结方案、引桥支座摩擦系数分别取0.01、0.03、0.05的情况。

从图10可以看出，振子的相对位移受周期比T1/T2和阻尼比之比ξ1/ξ2影响显著。除周期比为5.48工况外，相对位移均随阻尼比之比接近于1.0而逐渐减小，说明当两种结构周期相差较大时，减小阻尼比差异对控制相对位移无明显改善作用，只有当周期较为接近时，可以通过减小两者的阻尼差异进一步降低相对位移。值得注意的是，即使对应相同的周期和等效阻尼比，不同的阻尼机制也会导致相对位移的发生，如图11所示，振子①和②的周期均为3.87 s，等效阻尼比均为0.25，但摩擦阻尼振子的衰减速度要快于粘滞阻尼，导致两者相对位移的产生。图10还给出了主桥采用仅塔梁固结方案（无附加阻尼）、引桥摩擦摆支座摩阻系数分别取0.01、0.03和0.05的工况，可以看出，无附加阻尼状况下主桥的阻尼远低于引桥。进一步考虑在主桥每个辅助墩设两个粘滞阻尼器，其中阻尼指数0.3，单个阻尼系数400～4 000 kN·（s·m－1）0.3，通过非线性时程分析计算各工况下的结构响应，并根据阻尼器的滞回耗能计算其等效阻尼比绘于图中。可以看出，实桥的计算结果与单自由度振子具有基本相同的规律性，即当主桥周期与引桥接近、等效阻尼比也靠近引桥的阻尼水平时，相对位移可以得到较好地控制。实桥的结果大致介于两种单自由度振子之间，这主要是因为实桥结构的地震响应存在多阶振型参与，另外引桥的阻尼机制虽然主要源于支座摩擦，但不同墩位处的支座摩擦响应并不完全同步，此外结构的内阻尼为粘滞阻尼。由此可见，主、引桥的阻尼特性差异对其相对位移存在显著的影响，并且这种影响既有阻尼比大小的影响，也存在不同阻尼机制的影响。

图10 单自由度模型与实桥相对位移Fig.10 Relative displacements of the single degree of freedom model and the actual bridge

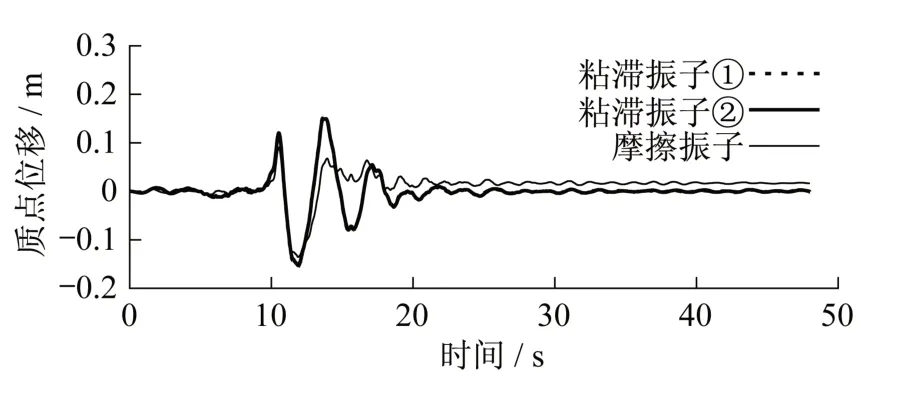
图11 单自由度模型位移时程（T1/T2=1，ξ1/ξ2=1）Fig.11 Displacement time history of the single degree of freedom model(T1/T2=1 and,ξ1/ξ2=1)

龙卷风图法（tornado diagram）是参数敏感性分析常用的方法之一，以各分析参数的相同概率分布区间为上下界，获得相应的响应变幅，将此变幅按由宽到窄的顺序从上至下排列，形成类似龙卷风形状的图形，反应的变幅越宽，意味着对应参数的敏感性越高［19］。根据前述单自由度体系周期比和阻尼比之比参数影响分析，选择周期比T1/T2的分析区间为（0.75，1.25）、阻尼比之比ξ1/ξ2的分析区间为（0.25，0.5），区间内的分布均为均匀分布。为保证各工况具有相同宽度的概率分布区间，确定共7种分析工况如表4所示，计算得到的龙卷风图见图12。从图中可看出，周期比B工况的变幅最大，阻尼比之比A工况的变幅最窄，相对位移对周期比的敏感性更强。由此可见，减小主-引桥相对位移应优先匹配主、引桥的周期，再控制阻尼差异的影响。

图12 梁端相对位移龙卷风图Fig.12 Tornado diagram of relative displacements

表4 分析工况与参数Tab.4 Analysis cases and parameters

4 主-引桥相对位移控制

主桥的三种抗震设计方案中，仅塔梁固结方案的主、引桥周期最为接近，对降低相对位移更具优势，因此选择该方案作为主桥的结构抗震设计方案。

对于主-引桥相对位移的进一步控制，首先，考虑到主桥的阻尼水平比引桥低很多，控制主-引桥相对位移可从增加主桥阻尼水平入手；其次，根据Caltrans规范，可在主、引桥梁-梁之间直接设置阻尼器以降低两者异步运动，减小相对位移；此外，本文还考虑同时增加主桥阻尼和设置主、引桥梁-梁阻尼器的方案。众所周知，粘滞阻尼器以其优越的减震效果在大跨度桥梁中备受青睐，以上三种减震方案的阻尼器均选用粘滞阻尼器。具体的布置方案：①在主桥各辅助墩上均匀布置粘滞阻尼器；②仅在主桥与西引桥的梁-梁之间设置阻尼器；③将一半的阻尼器分散布置在主桥辅助墩和主梁之间，另一半的阻尼器布置在主、引桥梁-梁之间。为对比不同方案的减震效果，各方案保持全桥阻尼系数总和不变，进行阻尼器参数敏感性分析，其中全桥阻尼系数总和的取值为2 000、5 000、8 000 kN·（s·m－1）0.3，阻尼指数取0.3，引桥摩擦摆支座摩擦系数均取0.03（对应主、引桥周期比1.0）。通过非线性时程分析，得到各工况下的主引桥相对位移响应如下表5所示。

表5 各方案主引桥相对位移Tab.5 Relative displacement of the main and approach bridge end of each scheme m

由表中结果可知，三种方案的主-引桥相对位移均随着总阻尼系数的增加而下降，但不同方案对相对位移的控制效果不同。直接在主、引桥梁-梁之间布设阻尼器的方案②抑制效果最好，各阻尼系数工况下相对位移均最小，阻尼系数在C=2 000～8 000 kN·（s·m－1）0.3变 化 范 围 内，相 对 位 移 降 低 了22.2%；方案③次之；方案①的控制效果最弱，主、引桥相对位移仅降低10.5%。图13给出了总阻尼系数C=8 000 kN·（s·m－1）0.3时的三种方案的主、引桥梁端位移时程及相对位移时程。可以看出，由于大跨度斜拉桥主、引桥阻尼特性差距过大，仅依靠附加阻尼器增加主桥阻尼比对提高主、引桥阻尼比接近程度无明显效果，因此图13a中主桥的主梁衰减速度仍远低于引桥，导致较大的相对位移。直接在主、引桥梁-梁之间设置阻尼器，利用结构间的相互运动来消耗和吸收振动能量，减小了相邻桥跨的阻尼特性差异；Zhang等［20］指出在相邻结构间设置粘滞阻尼器后，结构位移响应随着阻尼系数增大而趋于一致，图13b中主桥的梁端衰减加快而引桥的则减慢，在很大程度上使主、引桥的主梁位移同步性提高有效抑制了相对位移响应。同时在主桥各墩位处和主、引桥梁-梁之间设置阻尼器时，阻尼器兼具前两种方案中的作用，响应也介于前两者之间。

图13 不同方案的主、引桥梁端位移与相对位移时程Fig.13 Comparison of displacement time history of the main,approach bridge girder displacement and relative displacement

需要指出的是，尽管方案②对控制主-引桥相对位移的效果最大，但若将所有阻尼器均安置在主引桥梁-梁连接处易受安装空间限制，且考虑结构温度效应所需的冲程和累积行程均较大，此外集中布置将导致梁端的受力更加不利，尤其是所需的阻尼器受力较大时，例如μ=0.03、C=20 000 kN·（s·m－1）0.3工况下梁端阻尼器的阻尼力达到1 232 t。因此，兼顾主桥阻尼提升和主、引桥梁-梁相对运动控制的方案③仍不失为一个适应性较好的方案。

针对方案②和方案③，进一步开展参数敏感性分析，阻尼系数C取值范围2 000～20 000 kN·（s·m－1）0.3；引桥摩擦摆支座的摩擦系数μ分别取0.01、0.03和0.05，结果如图14所示。可以看出，两个方案均对应摩擦系数取μ=0.03时（周期比约为1.0）的相对位移最小，这再次印证了第3节所述的周期比敏感性分析结论。此外，对比图14a和14b可以看出，随着阻尼系数的增大，方案②对相对位移的控制效果相较方案③略具优势，但对于结构周期比为1.0的工况（μ=0.03）两种方案相差并不大，并且对于大吨位阻尼器方案③分布更加均匀，C=20 000 kN·（s·m－1）0.3工况下单个阻尼器的最大阻尼力为668 t，相比方案②集中布置的单个阻尼器受力更小，适应性更高，具体可根据实际情况酌情优选。

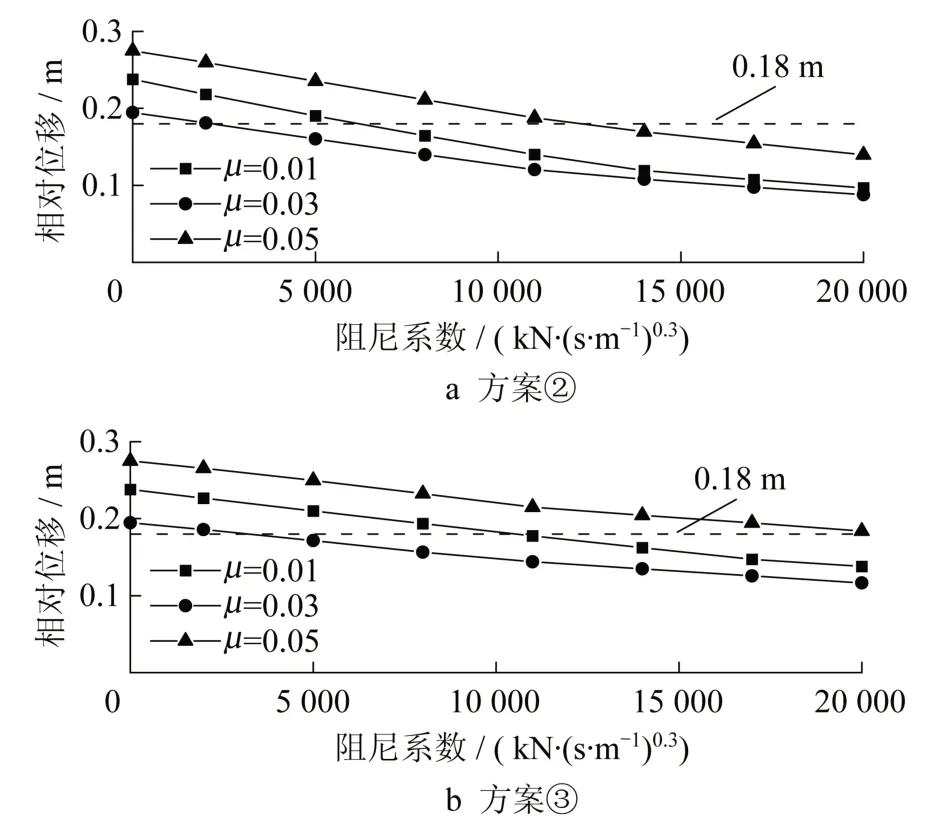
图14 主引桥梁端相对位移Fig.14 Relative displacements of the main-approach bridge ends

5 结论

本文基于巴拿马运河四桥，研究了大跨公轨合建斜拉桥的主-引桥相对位移的影响要素和控制问题。建立了全漂浮、固结和仅塔梁固结抗震设计方案模型，分析了三种约束方案的相对位移响应。基于单振子模型研究了相邻结构周期比T1/T2和阻尼比之比ξ1/ξ2对相对位移的影响，并在此基础上，结合理论和参数分析研究了主-引桥相对位移的控制方法。主要结论如下：

（1）高墩大跨公轨合建斜拉桥结构自身柔度较大，结构地震动内力响应较小，安全性设防地震下的结构性能并不控制设计，功能性设防地震下的主-引桥相对位移控制问题相对更为突出。

（2）相邻结构在地震作用下的相对位移不仅受周期差异的影响，等效阻尼比大小和不同的阻尼机制也会产生显著影响。在敏感性分析中，相邻结构周期比T1/T2在0.75～1.00变化时，大跨度斜拉桥主-引桥相对位移降幅最大，相比阻尼比之比ξ1/ξ2在0.25～0.5范围内的相对位移降幅大60%，因此相对位移对周期比的变化更加敏感，应优先调整主、引桥的周期差异，同时尽可能地协调其阻尼差异。推荐巴拿马四桥主桥采用仅塔梁固结方案，引桥支座摩擦系数取0.03。

（3）不同阻尼器布置方案对主-引桥相对位移的控制效果不同。增加主桥阻尼可以降低主-西引桥的相对位移，但效果相对较弱，随着阻尼系数由2 000增大到8 000 kN·（s·m－1）0.3，相对位移降幅仅为10.5%；直接在主-引桥梁-梁之间设置阻尼器，可以协调主引桥的运动，对相对位移的减震效果最好，各阻尼系数工况下控制相对位移最小，且降幅达到了22.2%；同时在主桥各墩位处和主、引桥梁-梁之间设置阻尼器的减震效果次之，但适应性更好。

作者贡献声明：

管仲国：提出理论及指导论文撰写。

徐瑜窈：理论验证分析、数值计算及撰写论文。

郑志均：整理并提供资料。