联合卫星定位和测量机器人的超高层建造过程水平位移监测
黄善琪,段志钦,吴玖荣,陈俊平
(1.广西大学土木建筑工程学院,广西南宁 530004;2.广州大学土木工程学院,广东广州 510006;3.中国科学院上海天文台,上海 200030)
不规则结构超高层建筑正逐渐成为城市新地标,对其进行安全监测已逐渐成为当下的研究热点[1-3]。因为不规则结构设计本身会带来的扭转和偏心,在设计时便规定了它们在建造和竣工时的水平位移阈值。因此在建造期间准确获得其水平位移对于保证建造过程和使用期间的安全具有重要意义[4-5]。常用的监测方法是对结构变形敏感位置进行周期观测。设计时通过有限元分析可以获得建筑结构随荷载增加的变形结果。通过对该结果的分析,监测点一般布设在位于中间楼层变形拐点处。使用全站仪/自动测量机器人(robotic total station,RTS)在地面控制点上对监测点进行测量是行之有效的方法。RTS因高自动化、高精度等特点被广泛用于大坝、桥梁等构造物的变形监测[6-8]。对于超高层建筑而言,RTS获得的瞬时点位精度受以下因素的影响:控制点稳定性、大气延迟和建筑晃动。控制点稳定性可以采用定期控制网复测予以削弱;大气延迟的影响可以通过选择适当的观测时间、加入适当的模型等方式削弱;随着建造高度不断上升,建筑晃动不可避免,其已成为影响监测精度的主要误差来源。荷载变化是超高层建筑晃动的主要原因,而日照、温度等大气因素也会影响晃动的频率和幅度[9]。在迪拜塔的建造过程中,选择在塔吊不工作的清晨进行测量以削弱晃动的影响[10]。该方法存在如下限制:首先,该方案无法有效消除载荷的影响;其次,随着监测点数增加,监测耗时较长,观测时间将显著超出清晨这一时段。
使用全球卫星定位技术(global navigation satellite system,GNSS)可以全天候、高效地监测超高 层 建 筑 晃 动[11-13]。使 用GPS(global position system)接收机运用RTK(real-time kinematic)技术能够准确获得建筑顶部的水平位移和振动频率[14];对位移序列的谱分析结果表明监测结果能够精确识别高耸结构的低阶振动频率[15]。但是,GNSS技术对点位观测条件要求较高,因此只能用于观测楼顶的晃动[2,16],无法测量位于中间楼层的监测点变形。中间楼层瞬时晃动量若可以通过楼顶的晃动频率和振幅内插获得,即可以削弱晃动对RTS瞬时监测结果的影响。为此,本文将从实测数据出发,讨论GNSS辅助RTS削弱建筑晃动影响的有效性。然后将该方法用于实际项目的长期监测中。结果表明:该方法能够有效结合GNSS和RTS各自的优点,不增加各自的操作复杂度;有效削弱建筑晃动对RTS观测结果的影响,监测结果更加平滑且与数值分析结果更符合。
1 数学方法
GNSS和RTS均可获得点位变化序列,为验证GNSS辅助RTS削弱晃动影响之有效性需要验证GNSS获得的楼顶监测点与RTS获得的中间楼层监测点的晃动信息具有相同的频率。为此,本文引入Hibert-Huang变换(HHT)提取点位变化结果的频率。此外,还需要验证楼顶它们两者之前晃动的大小是否具有线性关系,为此将GNSS获得的楼顶晃动内插至中间楼层以比较两者的相关性。
1.1 频谱分析方法
HHT是为分析非稳定或非线性数据信号而设计的信号处理方法,由美籍华人黄锷在希尔伯特变换的基础上提出[17]。超高层建筑的变形监测常使用该方法对数据进行处理[18-19]。HHT的核心是经验模态分解(empirical mode decomposition,EMD),将复杂的数据分解成多个固有模态函数(intrinsic mode function,IMF),然后通过希尔伯特变换得到其瞬时频率,分析频谱成份。该方法将原始信号在不同频带内进行分解和重构,在分解得到的高频分量中能够明显地看到损伤引起的突变信号。通过傅里叶变换,将时域内观测的数据转换成频域内进行分析;功率谱密度分析(power spectral density,PSD)定义了动态观测信号时间序列的能量如何随频率分布;对重构信号的功率谱密度函数运用谱峰法进行分析,可以较精确地识别出结构的模态参数[20]。本文使用的HHT的流程图如图1所示。
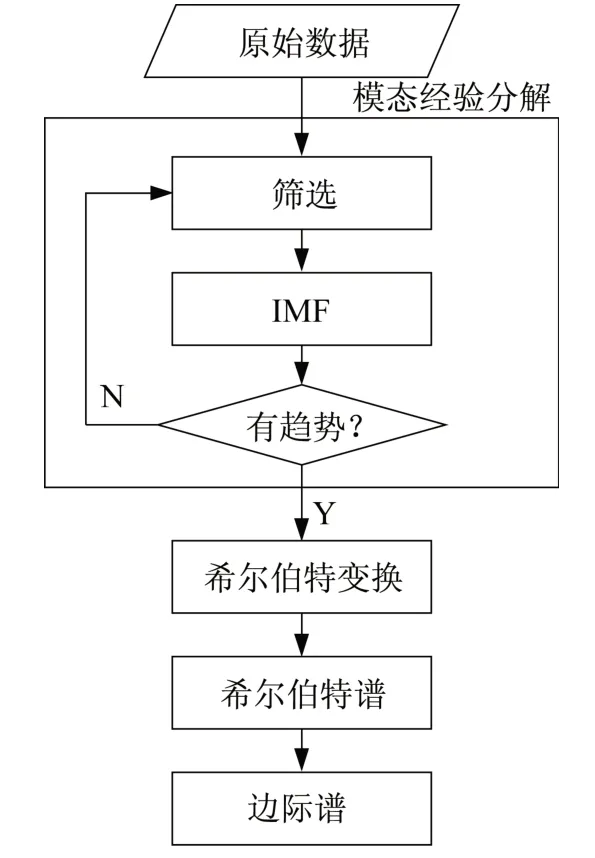
图1 HHT流程图Fig.1 Flowchart of HHT transformation
对于任意一个时间序列数据X(t),首先进行IMF分解,步骤参考文献[21]。原有时间序列可表示为
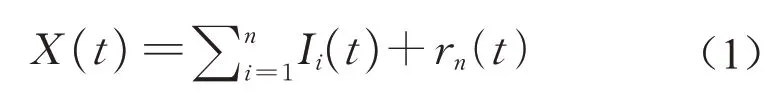
式中:Ii(t)为IMF信号分量;rn(t)为剩余信号分量。接下来,进行希尔伯特变换:
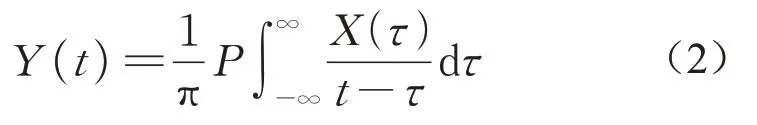
式中:P为积分的柯西主值,其避免掉τ=t和τ=±∞等处的奇点。通过这个变换,X(t)和Y(t)可组成一个复数信号Z(t):

定义瞬时频率ω(t)为

由式(4)可看出,ω(t)是时间t的单值函数,即某一时间对应某一频率。为了使瞬时频率有意义,作希尔伯特变换的时间序列数据必须是单组分的,而经验模态分解后的本征模函数序列恰好满足这个要求。把式(2)—(4)所表示的变换用于每个本征模函数序列,数据便可表示为
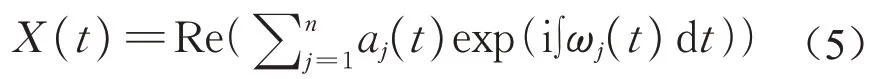
式中:Re()是取复数之实数部分的算子;exp()表示以自然常数e为底的指数函数。在这里忽略了残余项rn,因为它不过是单调函数或常数值。同样的,数据傅立叶变换的表示为
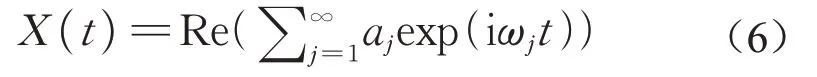
比较式(5)和(6),可以看到式(5)是式(6)的广义傅立叶表达。式(6)的频率ωj和幅值aj是常量,ωj、aj可构成二维傅立叶幅值频谱图;式(5)的频率ωj(t)和幅值aj(t)是时间的变量,可构成时间、频率、幅值的三维时频谱图,称为希尔伯特谱H(ω,t)。
最后求边际谱h(ω):
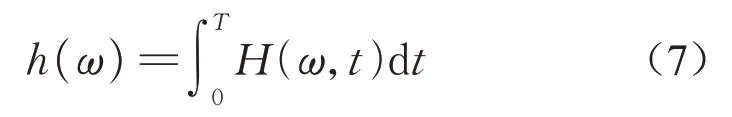
式中:T为序列的时间长度,把三维时频谱经过对时间的积分,便形成了只有频率和幅值的二维谱图,边际谱从统计意义上表征了整组数据每个频率点的积累幅值分布。
1.2 瞬时晃动值内插
GNSS接收机位于超高层建筑顶部,而RTS监测点位于中部楼层,需要利用内插的方法将GNSS获得的晃动监测结果归算到监测点所在的楼层。超高层建筑晃动随楼层高度的分布一直是当下研究的难点。一般而言,超高层建筑在设计时会通过有限元分析获得其变形量,因为载荷分布不均匀的原因,大部分超高层建筑水平变形并不呈线性变化。但是,本文的目标是削弱而非完全消除建筑晃动的影响。由于荷载随高度不断堆积,越往上荷载越大,受风力等因素的影响也越大,在建筑建造标高不是很大时可以将其晃动随高度的变化简化为线性模型。大部分时候监测时的本文的研究的超高层建筑建造标高远小于400 m,风洞试验表明高度约为400 m的超高层建筑水平位移瞬时响应可以近似认为是线性的[22];数值分析[23]、均匀分布在多个楼层的加速度传感器的实测数据[24],也获得相似的结论。需要特别说明的是,超高层建筑顶部瞬时位移除了晃动之外还包括持续位移的影响,因此晃动需要扣除持续位移的影响。持续位移可以用长期固定在爬模顶部的GNSS接收机每天计算一个结果得到。
超高层建筑底部与基础相连可以认为晃动为零,而顶部为所有力累加的结果,设扣除持续位移影响后的残余瞬时变形量的南北方向分量为Δdx,GNSS接收机的建筑标高为HR。中间楼层某个监测点的建筑标高为HM,则该监测点南北方向晃动的影响可以通过线性内插得到:
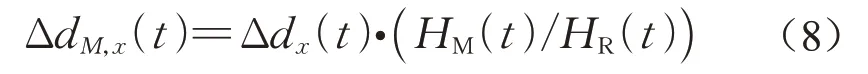
式中:下标t是指内插计算时的时间。东西方向位移量也可以通过类似的方法计算。
2 实验分析
选用在建的南宁某写字楼项目进行实验。该超高层建筑建成后楼高为406 m,使用核心筒加钢构的施工工艺。核心筒施工采用顶模浇筑的方式。实验选用Leica TM30自动测量机器人对中间楼层的监测点进行动态位移测量。同时利用GNSS测量同一时间该超高层建筑顶部的晃动。在顶模上安装两台高采样频率Leica GS15接收机实时监控楼顶变形,它们分别位于顶模的东北角(命名为“NE”)和西南角(命名为“SW”)。在封顶之后,这两台接收机被固定在核心筒主墙顶端。在距离该超高层建筑约500 m的稳定点上架设另一台GS15接收机作为基准站。该稳定点位于一栋已建成5年以上的商场顶部,建筑标高约46.3 m,是RTS监测的控制网的站点之一,采用南宁市地方独立直角坐标系。
2.1 有效性检验实验
实验主要目的是验证GNSS辅助RTS削弱建筑晃动对其监测结果影响的有效性,主要从两方面进行分析:楼顶和中间楼层晃动频率的一致性;楼顶振幅内插结果与中间楼层振幅的一致性。为此,实验时建筑顶模施工标高为201.35 m,GNSS接收机标高为199.89 m。RTS架设在基准站旁边2 m的稳定点上。利用RTS监测31M楼层的监测点,监测点标高131.35 m,采样频率为5 Hz。该点X(南北方向)、Y(东西方向)的动位移时程曲线图如图2所示。X方向的变形在±3 cm之内,Y方向变形绝大部分在±2 cm之内。对全站仪水平位移测量监测点所获得的X、Y方向的动位移时程曲线分别进行PSD分析,结果如图3所示。
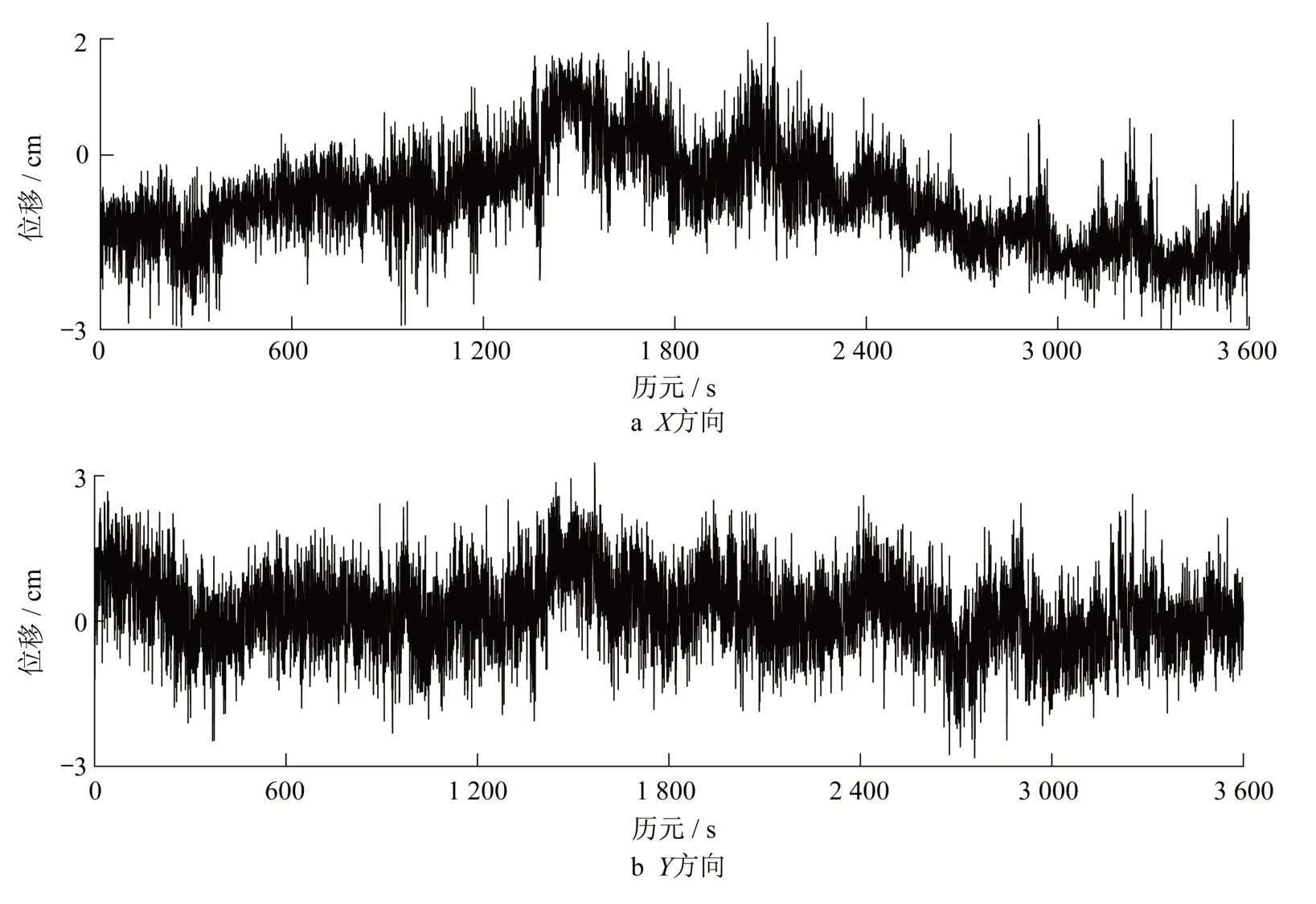
图2 31层监测点变形时间序列Fig.2 Displacement time series of monitoring point in the 31Mlayer
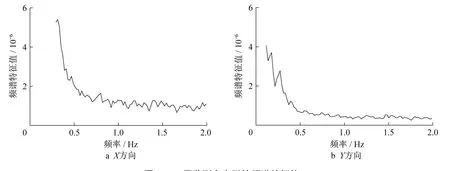
图3 31层监测点变形的频谱特征值Fig.3 Spectrum characteristics of monitoring point in the 31M layer
两个主轴方向最低自振频率分别为0.254 Hz和0.288 Hz。
位于楼顶的两台GNSS同时采集数据,采样频率为5 Hz,GNSS时间序列结果均通过重名点计算的转换参数换算为南宁市地方独立直角坐标系。NE和SW相应时段的变形时序分别如图4和图5所示。NE和SW在X、Y方向上的频谱分析结果分别如图6和图7所示。从图中可以看到,NE在两个主轴方向的最低阶自振频率分别为0.273和0.293 Hz。SW在两个主轴方向的最低阶自振频率分别为0.234和0.293 Hz。比较图3和图6、图7,GNSS的率谱分析结果与全站仪得到的结果相对差值在10%以内,可认为两者具有接近的晃动频率。

图4 NE位移量时间序列Fig.4 Displacement time series of NE
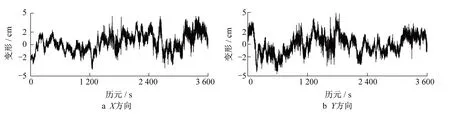
图5 SW位移量时间序列Fig.5 Displacement time series of SW
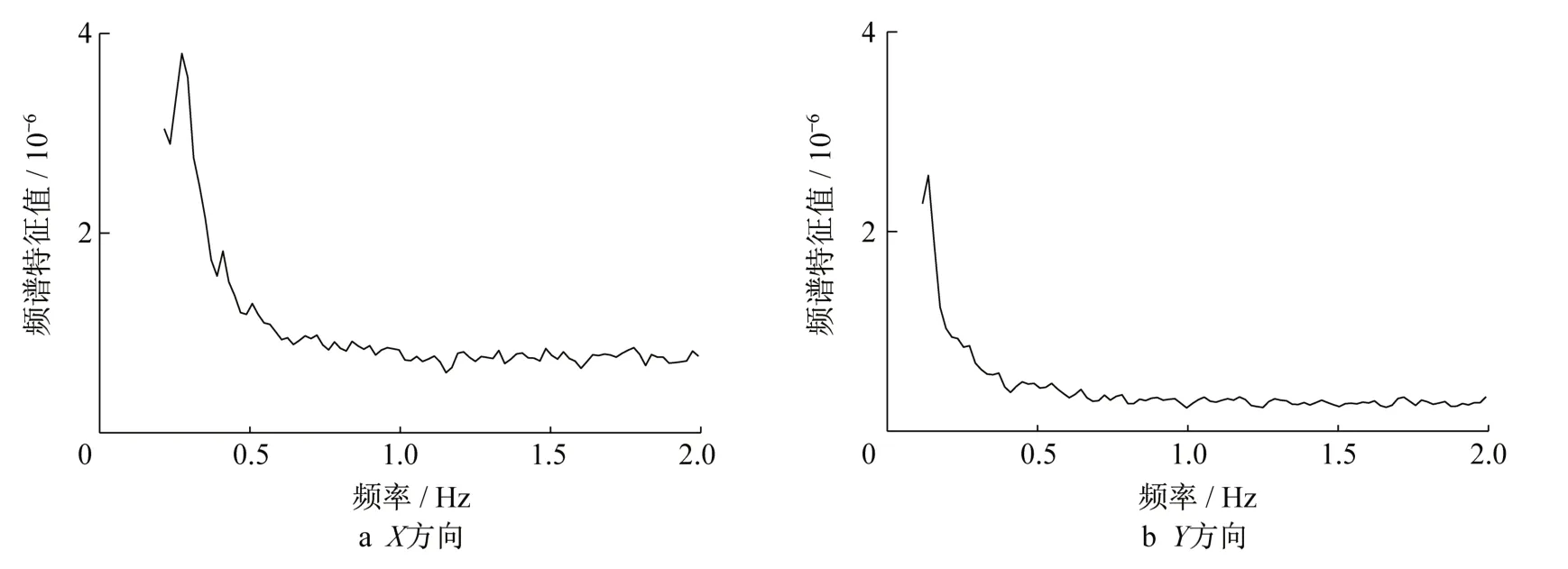
图6 NE变形的频谱特征值Fig.6 Spectrum characteristics of NE
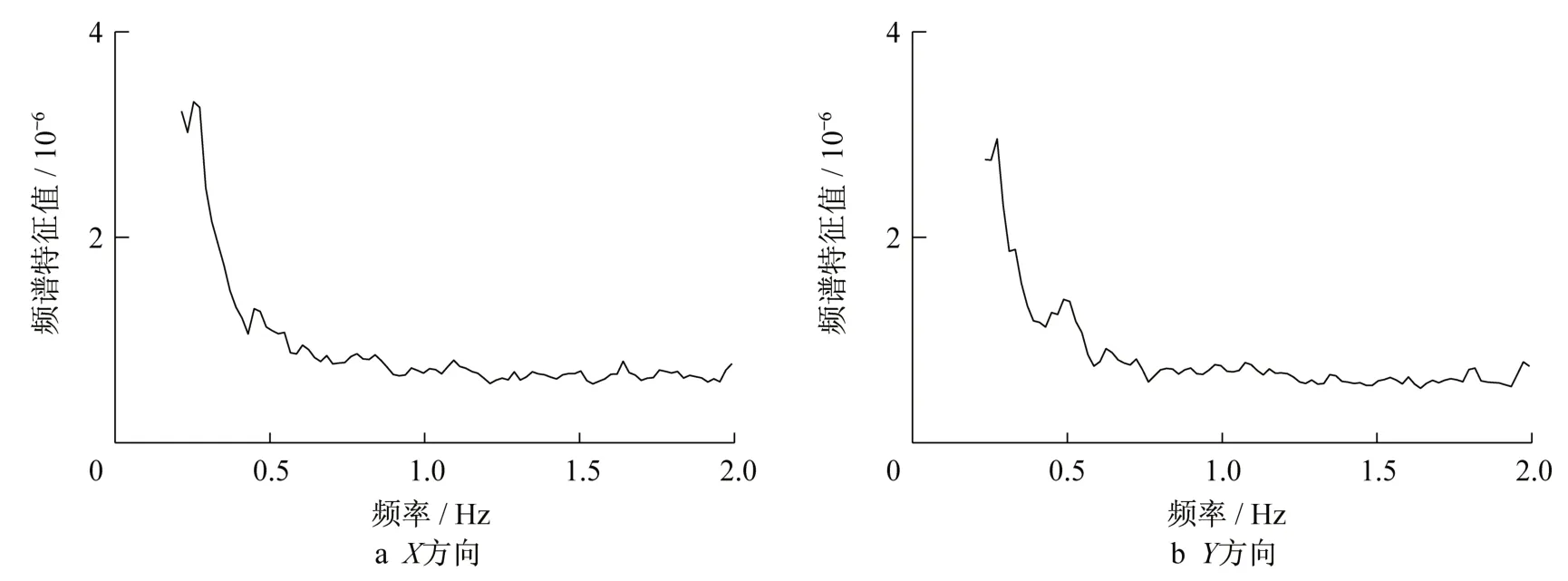
图7 SW变形的频谱特征值Fig.7 Spectrum characteristics of SW
SW离31M监测点的水平距离较近,其解算结果内插得到31M楼层的水平位移与RTS测量结果的对比如图8所示。GNSS结果因大量高频噪声的存在而波动较大,RTS测量结果的波动要小得多。从图中可以看到,除了数据的头尾两部分以外,两者的吻合度较好(相关系数为0.82)。这说明通过内插获得中间楼层瞬时水平位移在RTS测得的瞬时监测结果中予以扣除可以削弱晃动带来的大部分影响。
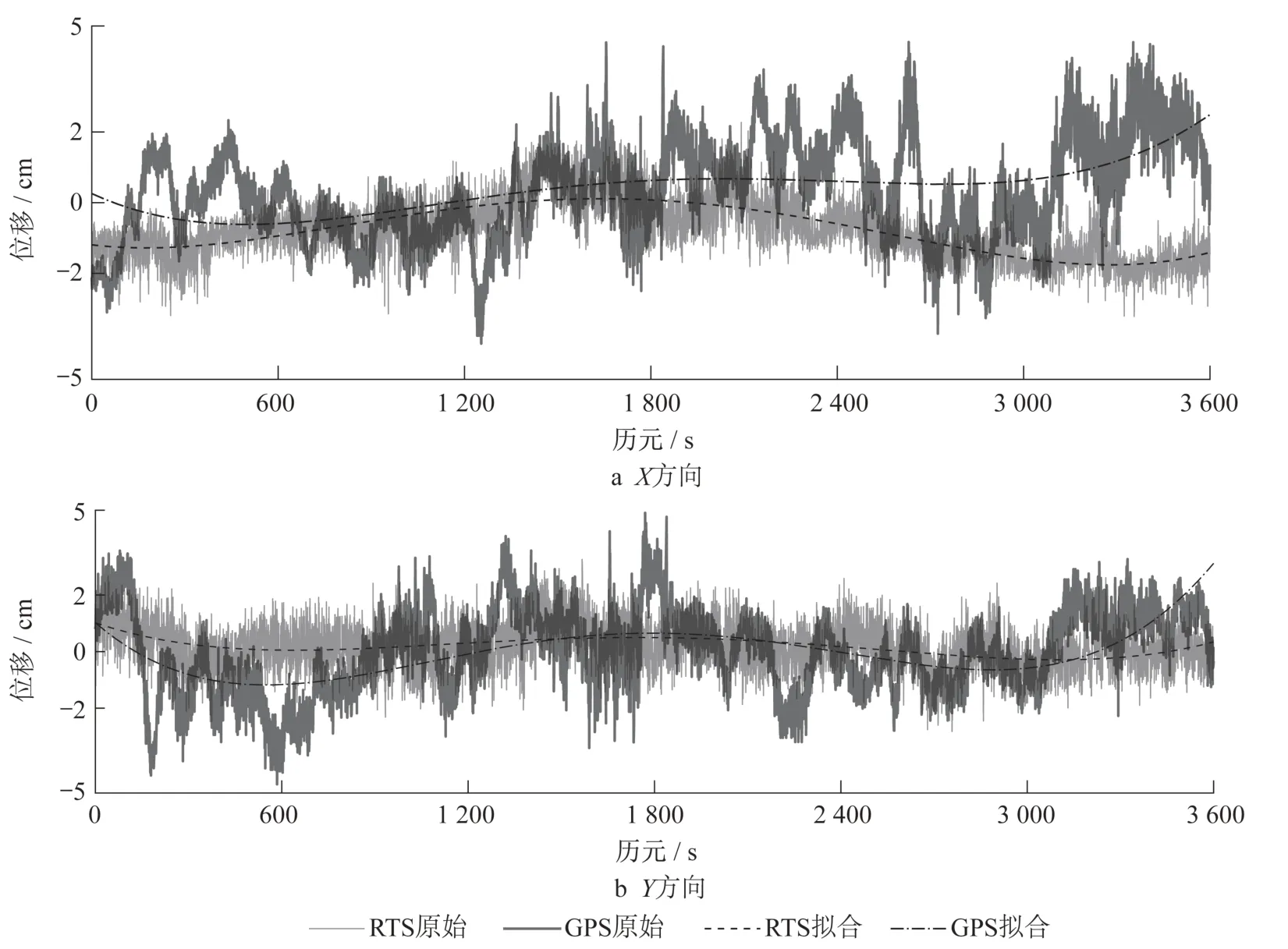
图8 GNSS结果与RTS结果的比较Fig.8 Comparison the results of GNSS and RTS
2.2 长期观测实验数据分析
对该项目进行了施工过程水平位移的全过程监测。接下来分析GNSS辅助RTS削弱建筑晃动影响的监测方法对于长期监测结果的改进效果:首先比较使用了新方法的结果和未使用该方法的结果;其次是比较使用了新方法的结果和有限元分析的结果。
结合塔楼变形模拟的情况,在19M、31M、44M、58、63、66、68、71、74、76、80、85每层设置8~16个,共计96个水平位移观测点。其中,每层有4~6个水平位移监测点在核心筒上;6~10个监测点位于外框柱上。随着建造高度不断升高至相应楼层时即布设该楼层的监测点。以31M层为例,点位的分布如图9a所示。随着核心筒收缩,点数会减少,但是在相同位置的点编号保持一致。在建造期内,每上升4层进行一期监测;核心筒封顶之后每个月进行一期监测。监测控制网布设在该超高层建筑各方向一定距离的稳定地面上,每两个月复测一次。

图9 监测点分布图Fig.9 Deployment of MPs
规范规定的水平位移阈值为每一层中心点的偏移量。在本项目中,每个楼层中点的变形量由该层所有观测点的结果通过反距离加权平均的方式获得,其中权重设为该监测点到中心的距离倒数。接下来以68层为例进行分析。从有限元分析的结果(图10)来看,该层是变形较大的楼层,从第8期测量开始有观测数据。该楼层从第8期至27期未消除晃动影响的原始观测结果如图11a所示,图中每个点的标记是指期数。利用GNSS数据削弱晃动影响后的结果如图11b所示。比较两个结果,RTS原始监测结果跳变较大,即使使用三次拟合,离散度仍高达25.3%;若使用线性拟合,离散度达到48.4%。新方法削弱了建筑晃动的影响,监测结果更为平滑,与变形的特性更加相符。使用直线拟合,离散度仅为9.3%。截至到封顶时,所有楼层变形量离散度的统计结果见表1。从对比可以看出,新方法可以显著抑制监测结果的不规则噪声,这也说明了建筑晃动是监测噪声的主要影响因素。
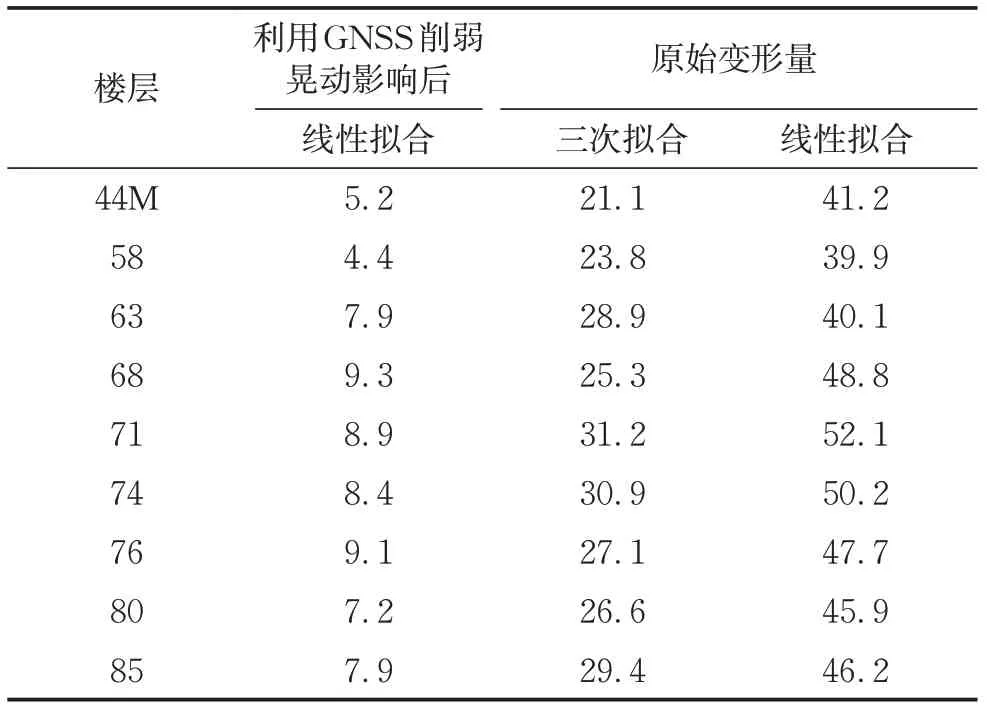
表1 所有楼层的离散统计Tab.1 Dispersion statistics of the monitoring results of all floors%
图10 ETABS有限元分析结果Fig.10 Results of ETABS finite element analysis
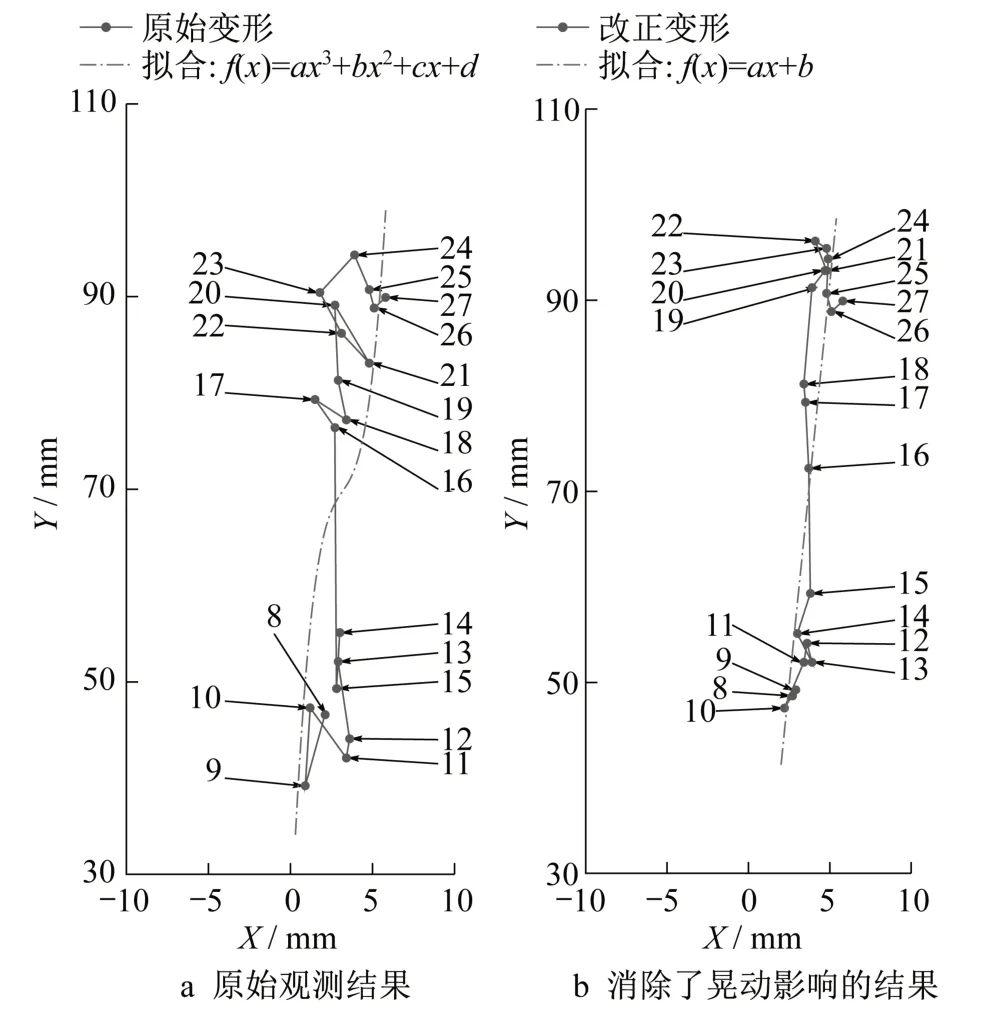
图11 68层中心水平位移序列图Fig.11 Results for the center of 68th floor
采用有限元软件ETABS 2013进行本建筑物在施工期间的力学仿真分析。荷载工况取1.0恒载+0.5活载,考虑了混凝土收缩徐变,施工阶段按施工计划步骤考虑,分析时间为施工开始至投入使用后20年。本工程收缩徐变模式参考深圳平安金融中心、上海中心大厦、天津周大福金融中心等项目采用CEB-FIP 90模型。施工模拟仿真分析的结构有限元模型如图12所示。在修筑到44M层、71层和封顶时,使用新方法后北边框上的14号监测点变形监测结果如图12a所示。相应位置有限元分析的结果如图12b所示。在修筑到44M层、71层时,变形趋势和变形量与有限元分析结果基本一致。在封顶时,实测结果变形趋势与有限元分析结果仍吻合较好。
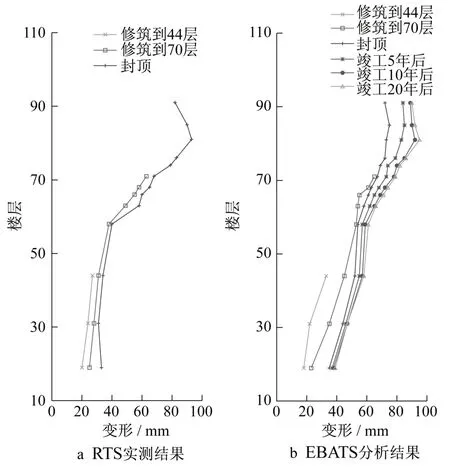
图12 不同楼层变形量Fig.12 Deformation of different floors
3 结论
为了建造安全,需要准确地获得不规则结构超高层建筑在施工过程中的水平位移。RTS适用于测量设置在中间楼层的监测点的变形,但其瞬时监测结果主要受建筑晃动的影响,导致监测结果离散度较大,趋势性不显著。GNSS技术不适用于监测中间楼层的水平位移,但可准确获取超高层建筑顶部的晃动。本文介绍了应用RTS技术监测超高层建筑中间层水平位移时,利用GNSS削弱建筑晃动影响的方法。首先,通过实验验证了该方法的可行性。结果表明,GNSS测得的晃动频率与RTS测得的晃动频率基本一致;在得到顶部瞬时幅值后,利用线性插值方法得到的中间层幅值与RTS测量值一致性较高。这说明建筑晃动对RTS结果的影响可以通过GNSS数据予以削弱。然后,利用该方法对某在建超高层建筑的长期监测数据进行了处理。结果表明,该方法能明显抑制监测结果的不规则抖动;计算结果与有限元分析结果吻合较好。
作者贡献声明:
黄善琪:论文主要构思者,负责模型构建,指导监测过程的仪器操作流程,处理监测数据,报告及论文写作。
段志钦:监测过程仪器操作,论文撰写。
吴玖荣:监测项目负责人,负责监测项目总体方案,有限元分析,测量结果与理论模型验证。
陈俊平:负责指导模型构建,数据处理,论文撰写。

