基于动态客流量模型的地铁车站空调负荷预测
苏 醒,王 磊,田少宸,秦 旭
(1.同济大学机械与能源工程学院,上海 201804;2.同济大学工程结构性能演化与控制教育部重点实验室,上海 200092;3.广州地铁设计研究院股份有限公司节能和环保技术中心,广东广州 510010)
地下轨道交通车站作为一种典型的公共建筑,单位建筑面积能耗是常规公共建筑的2~4倍[1],其中地铁车站通风空调系统能耗占整个地铁车站总能耗的比重约为30%~50%[2-4],节能潜力巨大。对地铁车站空调负荷的准确预测是实现空调系统优化控制和节能运行的前提。
机器学习算法逐渐应用于建筑空调负荷预测,主要包括人工神经网络(artificial neural network,ANN)和 支 持 向 量 机(support vector machine,SVM)等方法。Wang等[5]使用神经网络结合部分物理规则对建筑冷负荷进行了动态预测,显著提高了预测精度。近年来,SVM算法的预测方法得到了广泛应用。Chen等[6]将SVM算法应用于空调逐时负荷预测,并分别应用遗传算法、蚁群算法及粒子群算法对SVM的参数进行优化,预测结果表明这三种空调负荷预测模型的预测精度较高。Li等[7]比较了SVM和三种不同的ANN算法用于预测建筑逐时负荷的效果,发现SVM和广义回归神经网络算法预测精度更高。这些研究主要应用于人流量较为稳定的建筑,对于地铁车站,空调负荷受客流量影响更为明显,樊佳慧[8]采用结构模型解析方法对地铁车站环控负荷及其影响因素进行定性分析,发现主要影响因素为客流、室外气象参数和列车行车对数。李婷婷等[9]建立了基于BP(反向传播)神经网络的地铁站厅空调负荷预测模型,选取室外空气温度、室外空气相对湿度、人员数量、太阳辐射作为神经网络输入参数,利用TRNSYS软件对站厅空调负荷相关数据进行仿真,利用仿真数据对神经网络进行训练和测试,以期提高预测精度,但人员数量来源于调研,无法适应客流量的未来变化。付亮[10]利用遗传算法和粒子群算法优化误差反向传播神经网络(error back propagation neural network,BPNN)的权值和阈值,建立地铁车站空调负荷预测模型,但是在预测过程中,数据量较少且未考虑非工作日客流量不同的影响。
动态客流量参数精确计算也是预测的难点。地铁车站客流量的相关研究主要集中在两个方面。一种是通过经验公式估算确定,如梁园[11]根据客流在换乘车站进行换乘的方式不同,提出了4种不同的换乘车站公共区空调人员计算公式,根据时间段内上下车客流和乘客停留时间就可进行估算。这种方法只适用于设计阶段,且乘客停留时间根据经验确定,预测精度较低。第二种方法是利用自动售检票系统(automatic fare collection,AFC)数据进行推算,樊佳慧[8]提出了基于AFC数据与概率分布的乘客在站停留时间估计方法,从而实现对客流参数的精准计算。这种方法需要详细且数量庞大的AFC数据以及构建复杂的基于列车时刻表的时空拓展网络,工程实际应用较为困难。
考虑到大部分地铁车站内都对CO2体积浓度进行了多点监测,可能能够间接反映客流量的变化。本文选择广州某换乘车站为研究对象,首先通过相关性分析确定地铁车站空调负荷的关键影响因素,之后结合车站CO2浓度逐时监测数据和部分实测客流数据建立了动态客流量预测模型,以此为基础构建地铁车站空调负荷预测模型,并比较神经网络和支持向量机算法的负荷预测效果。
1 数据来源及处理
1.1 数据来源
本文数据来源于广州某地铁车站能耗监测平台,车站为“T”型换乘车站,设计早高峰客流量为40 213人·h-1,晚高峰客流量为47 623人·h-1。车站有一层站厅和两层站台共3层,中部为公共区,两端为设备区,设计有4个进出口,集中在站厅层中部。该车站对空调系统运行数据进行了监测和存储,已积累了三年的历史运行数据。数据有如下特点:
(1)数据量大:监测平台的最小数据采样间隔1 min,可提取完整的供冷周期的运行数据。
(2)缺少关键参数:本研究需提取的参数主要包括负荷、室外干球温度、室外湿球温度、客流量和列车行车对数,但是其中客流量和列车行车对数无法直接从监测平台获取,列车行车对数可从列车运行图得到,客流量具有时变性,也不易直接获取,可考虑用监测平台多个测点CO2体积浓度数据进行拟合替代。
(3)数据缺失:从数据平台提取不同变量、不同时间段数据会有不同的缺失情况,需要在预处理阶段进行相应的填充。
(4)数据异常:由于制冷机组、传感器等设备在运行过程中存在着性能失常、数据传输异常等情况,由此带来数据异常,难以直接识别。
地铁车站负荷预测需要从监测平台提取带有时间标签的室外干球温度、室外湿球温度以及多个测点的二氧化碳数据。本文的空调负荷预测主要是用于指导地铁车站空调系统的节能优化运行,需要的是逐时空调负荷预测值,属于短期空调负荷预测任务,因此需要收集的是近期半个月到几个月的历史数据,数据采样间隔为1 h。
1.2 数据预处理
1.2.1 缺失值填充
缺失值填充的方法主要有统计学方法和基于机器学习算法的方法。考虑到充分利用数据中的其他可用属性(部分属性值缺失),可以用机器学习算法来进行数据填充。常用的数据缺失值填充算法有k近邻(k-nearest neighbor,kNN)算法。kNN算法是基于某种距离度量,在训练集样本中找到与各个测试集样本距离最近的k个样本,并基于对应的k个样本信息对测试集样本的标签或者属性值进行预测。
1.2.2 异常数据处理
监测平台提取的数据有两种异常情况,一种是数据记录中单个数据属性会出现突变等情况,在时间序列上产生极端变化,这种异常肉眼可见,属于“显性异常”;另一种数据异常比较隐蔽,数据记录中每个数据属性在正常波动范围内,但是组成的数据点不符合客观规律,如客流量较大时,负荷反而较低,这种数据明显属于异常数据,需将各属性关联起来进行分析才能发现,属于“隐性异常”。其中“显性异常”数据识别起来较为简单,一般通过设定数据正常波动范围或者基于前后时刻数据差值进行判断即可解决。对于“隐性异常”数据的识别一般采用基于聚类的识别方法。k-means聚类,通过最小化簇内各样本与样本中心的平方误差来得到最优的划分结果,可用于判断“隐性异常”。
通过k-means聚类算法将样本集划分为k个样本簇之后,假设当某一个簇样本集很小时,视该簇数据样本为异常数据;此外在较大的样本簇中,假设正常数据样本距离簇中心较近,认为距离簇中心较远的数据样本为异常数据。
1.2.3 客流量参数计算
采用梁园[11]提出的换乘车站客流量计算方法,根据乘客在站厅、站台和换乘平台停留时间和车站客流情况,计算得出站厅、站台和换乘区的客流量参数。主要用于客流量预测验证,具体计算公式如下:
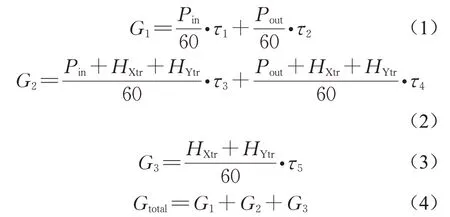
式(1)—(4)中:G1,G2,G3和Gtotal分别代表单位时间内站厅、站台、换乘平台和整个车站的有效客流量(考虑乘客停留时间),人·h-1;Pin,Pout代表单位时间内进站人数、出站人数,人·h-1;τ1,τ2,τ3,τ4,τ5分别代表进站和出站乘客站厅停留时间、上车和下车乘客站台停留时间以及换乘客流换乘平台停留时间,min;HXtr,HYtr分别代表X号线和Y号线单位时间内换乘客流量,人·h-1。
2 地铁车站空调负荷预测模型
以上述地铁车站能耗监测平台的历史数据作为数据来源,采样时间为2019年4月1日至2019年8月31日,采样间隔为1 h,经数据预处理后用于空调负荷预测。
2.1 地铁车站空调负荷影响因素分析
2.1.1 灰色关联度分析
灰色关联度分析是相关性分析方法的一种,通过比较因素变化曲线的几何形状相似程度,可判断不同因素之间的关联性。下面采用灰色关联度方法对车站空调负荷影响因素进行分析。
从地铁车站能耗监测平台提取2019年8月份逐时室外干球温度Td、室外湿球温度Tw以及对应时刻的负荷值Q,此外根据列车运行时刻表计算出不同时间段的列车行车对数Pa。由于监测平台缺少客流数据,而AFC数据中仅有进出站客流信息,对于换乘客流以及乘客停留时间等数据需进行现场实测得到。因此通过实测结合AFC数据得到地铁车站2019年8月份的进出站人数、换乘客流以及停留时间等信息,采用1.2.3节客流量参数计算方法,计算得到8月份逐时客流量参数G,Q、Td、Tw、Pa和G构成数据矩阵,其中Q为比较数据列,Td、Tw、Pa和G为参考数据列。对各指标进行量纲一处理,如式(5)所示。

式中:xmax和xmin分别为每个数据列中的最大值和最小值。
根据量纲一化后的比较数据列和参考数据列,按照式(6)计算对应关联系数ε。
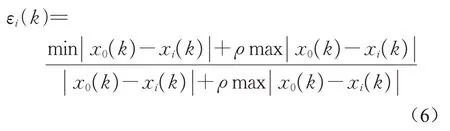
式中:x0(k)和xi(k)分别为比较数据列和参考数据列的第k个元素;ρ为分辨系数。
最后对关联系数求均值得到关联度。计算结果如表1所示。
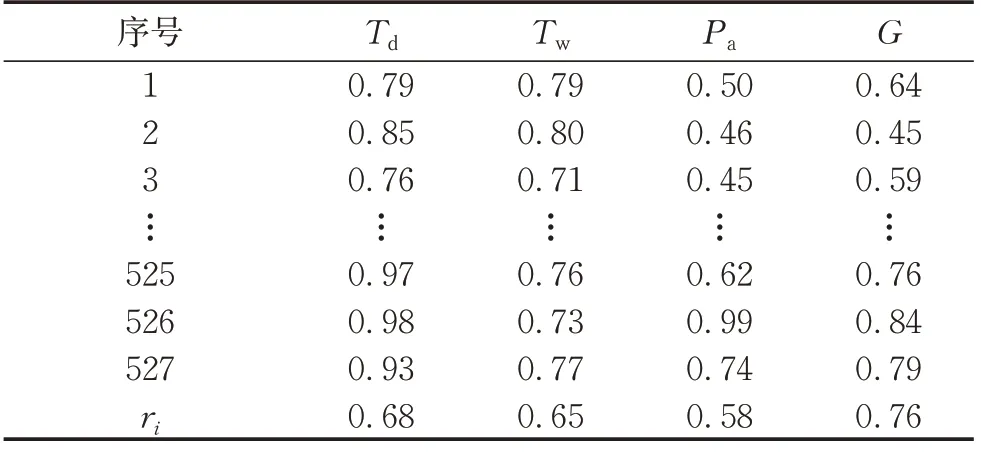
表1 关联系数计算结果Tab.1 Calculation result of correlation coefficient
灰色关联度的计算结果表明,客流量参数的关联度最大,室外干湿球温度次之,列车行车对数的关联度最小。说明客流的动态变化是地铁车站空调负荷具有时变性的主要影响因素,客流量的准确预测是车站空调负荷准确预测的基础。
2.1.2 确定输入变量
从2.1.1节分析中,确定地铁车站空调负荷预测的输入参数有:客流量、室外干球温度、室外湿球温度、是否为工作日(1/0)。考虑到客流量在一天内随着时间变化较为规律,故可以将预测时刻也纳入输入变量。采用灰色关联度分析方法,对预测时刻负荷和负荷的历史数据进行自相关性分析,结果如图1所示。从图中可以看出负荷历史数据和预测时刻负荷在不同时间间隔时相关性差异明显,以0.8作为阈值,选择时间间隔为1、2、3、23、24 h的负荷历史数据纳入负荷预测的输入变量中。
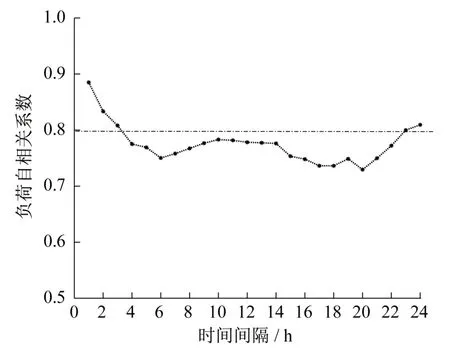
图1 负荷自相关系数变化图Fig.1 Autocorrelation coefficient change of cooling load
综上,确定地铁车站空调负荷预测输入变量为:①客流量G;②是否为工作日W(1/0);③预测时刻t;④室外干球温度Td;⑤室外湿球温度Tw;⑥预测时刻前1 h、2 h、3 h、23 h、24 h的空调负荷Q。故地铁车站空调负荷预测模型的结构为
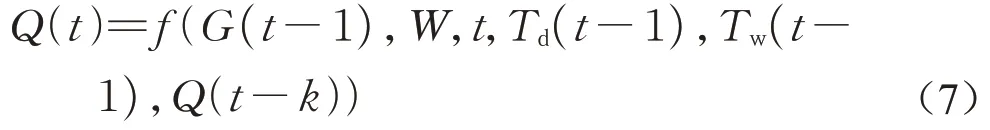
式中:k为预测时刻前1、2、3、23、24 h,分别取1、2、3、23、24。
2.2 基于CO2浓度数据的动态客流量预测
通过对车站监测平台新风量监测数据进行分析,发现其新风量供给量较为稳定,这也是目前许多车站的现状。此外,由于车站内CO2测点分布广泛,在车站内部远离出入口的CO2测点受出入口热压和风压作用下的自然通风量影响较小,本研究通过相关性分析对测点进行了判断和筛选。因此车站内部CO2测点能即时反映人员动态变化情况,且数据容易获取,可考虑采用CO2浓度数据对客流量进行拟合。
基于实测得到的2019年8月份的实际客流参数,从监测平台提取CO2浓度数据作为输入量,但是由于车站内部CO2监测点数量较多,分布在不同线路的站台、站厅以及换乘平台,采用灰色关联度进行分析,最终选择关联度超过0.75的三个测点,记为A、B和C。分别采用线性回归算法和神经网络算法建立客流量预测模型。并选用复相关系数R2和均方根误差(root mean square error,RMSE)这两个常用评价准则对拟合结果进行评价。
2.2.1 线性回归模型
根据相关性分析选择测点A、B、C的CO2体积浓度数据作为自变量,对应时刻客流量实测数据作为因变量,采用线性回归方法进行拟合。得到拟合关系式如下:
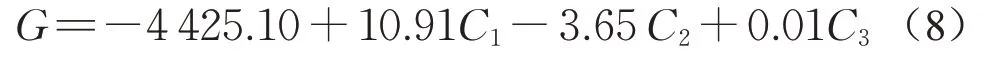
式中:C1为测点A的CO2浓度数据,10-6;C2为测点B的CO2浓度数据,10-6;C3为测点C的CO2浓度数据,10-6。
采用式(8)得到客流量预测值,与客流量实测数据进行比较,如图2所示,R2=0.83,NRMSE=348人·h-1,预测效果一般。
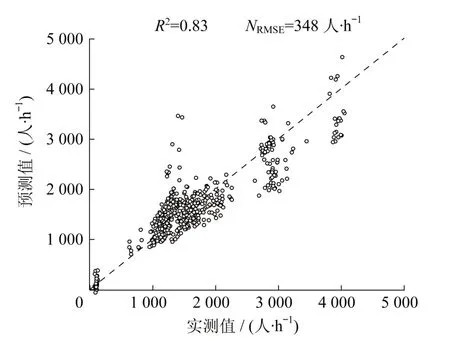
图2 线性回归客流量预测结果对比Fig.2 Comparison of linear regression passenger flow prediction results
2.2.2 神经网络模型
神经网络的概念来源于生物的神经元结构,是由具有超强自适应能力的简单神经元并行互连组成的网络[12],常用作预测算法。神经网络算法中应用最为广泛、最为成功的神经网络算法是误差反向传播神经网络算法。本文采用精度相对较高的BPNN模型进行客流量预测,输入变量为测点A、B、C的CO2浓度逐时数据,输出变量为对应时刻实测客流量参数。即输入层节点个数为3个,输出层节点个数为1个。隐含层节点的选取通过比较R2和RMSE进行选取,根据表2,数量设为7。
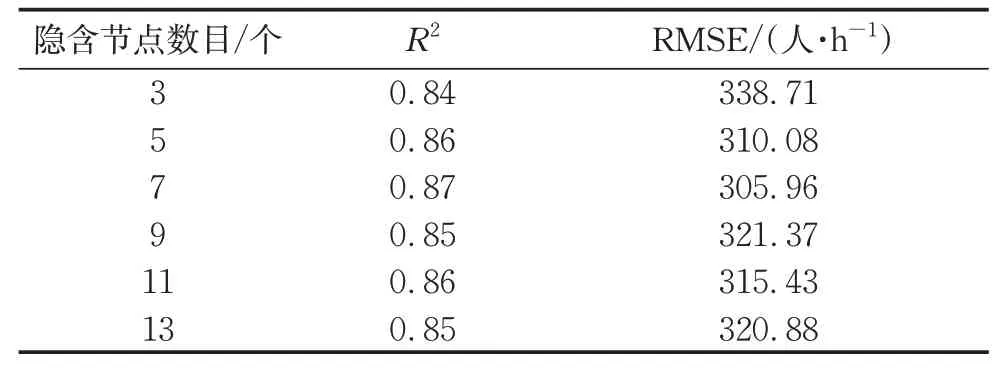
表2 不同隐含节点数目预测效果对比Tab.2 Predicting performance of different hidden node numbers
通过建立神经网络预测模型得到客流量预测值,与客流量实测数据进行比较,如图3所示,R2=0.87,NRMSE=306人·h-1,预测精度较高。
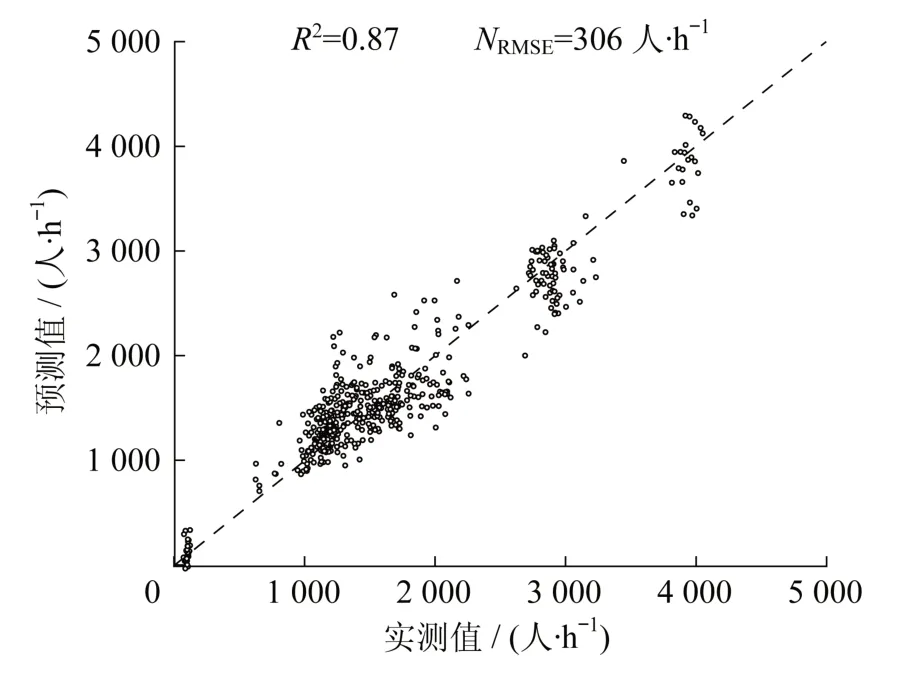
图3 神经网络客流量预测结果对比Fig.3 Comparison of passenger flow prediction results of BPNN
相比于线性回归方法,BPNN算法预测精度更高,更能有效反映客流变化趋势,这也表明采用CO2浓度预测地铁车站客流量的方法是可靠的,该模型预测得到的客流量可应用于负荷预测。
2.3 空调负荷预测模型比选
考虑到不同时间尺度的历史数据得到的模型可能存在差异,本节基于不同时间尺度历史数据,分别采用BPNN算法和SVM算法建立负荷预测模型,并比较两种模型在某一典型周(包含工作日和非工作日)的预测效果。选取2019年8月份的某一典型周(8月1日至8月7日)作为测试集,分别以8月份之前1个月历史数据(2019年7月份)、2个月历史数据(2019年6月份至7月份)、3个月历史数据(2019年5月份至7月份)、4个月历史数据(2019年4月份至7月份)作为训练数据。测试集的空调负荷逐时变化曲线如图4所示,从图中可以看出工作日负荷呈现明显的早高峰和晚高峰现象,非工作日(8月3日和8月4日)时负荷变化相对而言较为平缓。
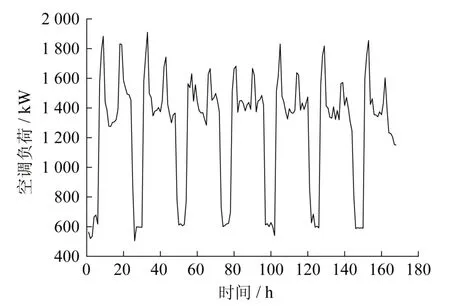
图4 测试集空调负荷逐时变化曲线Fig.4 Hourly variety curve of cooling load in the test set
2.3.1 基于BPNN算法的负荷预测
采用BPNN算法,分别以8月份之前1个月历史数据(2019年7月份)、2个月历史数据(2019年6月份至7月份)、3个月历史数据(2019年5月份至7月份)、4个月历史数据(2019年4月份至7月份)作为训练数据,在测试集上的预测结果如表3所示。当训练集时间尺度为4个月时,神经网络算法在测试集预测效果如图5所示。
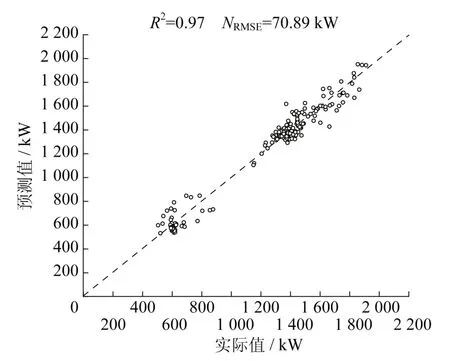
图5 神经网络算法负荷预测结果对比Fig.5 Comparison of cooling load prediction results of BPNN in the test set
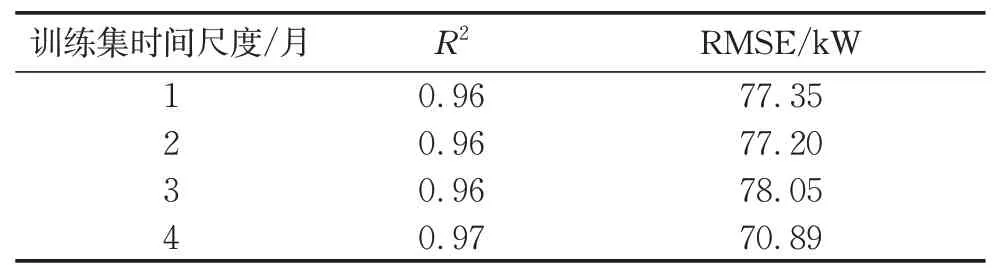
表3 不同时间尺度下BPNN算法预测结果Tab.3 Predicting results of ANN in different time scales
从不同时间尺度训练数据下BPNN算法的负荷预测结果可以看出,不同时间尺度下神经网络算法的预测效果并无明显差异,R2达到了0.96以上且RMSE在70~80 kW之间,预测效果良好。
2.3.2 基于SVM算法的负荷预测
SVM由Vapnik等[13]和N anye[14]提出,基本思想是将低维空间的非线性关系,经过维度变换(基变换),变成高维空间的线性关系。常见的基变化(也称核函数)包括线性核函数、多项式核函数、Sigmoid核函数和径向基核函数[15]。由于径向基核函数具有参数变量少、计算效率高等优点,选取径向基函数为核函数。不同时间尺度训练数据得到的负荷预测模型在典型周的预测结果如表4所示。当训练集时间尺度为2个月时,支持向量机算法在测试集预测效果如图6所示。可以看出,不同时间尺度下SVM算法的预测效果并没有明显差异,R2达到了0.95以上且RMSE在70~90 kW之间,预测效果良好。
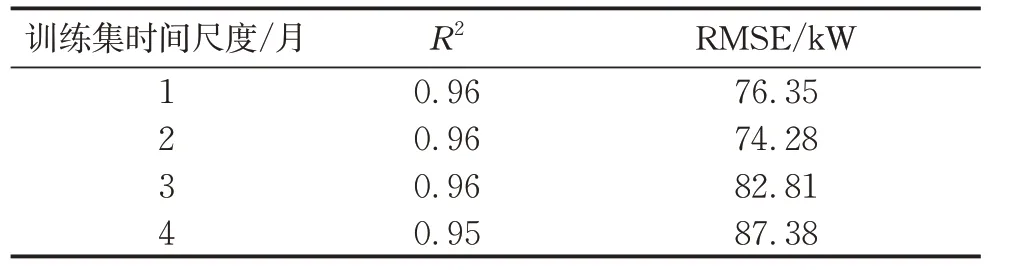
表4 不同时间尺度下SVM算法预测结果Tab.4 Predicting results of SVM under different time scales
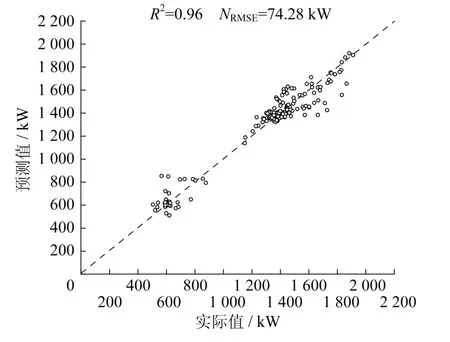
图6 支持向量机算法负荷预测结果对比Fig.6 Comparison of cooling load prediction results of SVM in the test set
对比神经网络算法和支持向量机算法的负荷预测效果,结果表明,当增加训练数据量时,两种算法的预测效果均无显著提升,R2达到了0.95以上,RMSE均在70~90 kW之间,均表现出了良好的预测效果。但是SVM算法的运算时间要长于BPNN,是BPNN算法的3~4倍左右,故当数据量较大时推荐BPNN算法。
3 结论
以广州某地铁车站为预测对象,基于地铁车站监测平台历史数据,建立动态客流量预测模型,并以此为基础,分别利用BPNN和SVM两种机器学习算法,建立了地铁车站空调负荷逐时预测模型。结论如下:
(1)利用灰色关联度方法对地铁车站空调负荷影响因素进行相关性分析,结果表明影响车站空调负荷的影响因素重要性排序为:客流量参数>室外气象参数>列车行车对数,客流量参数是影响负荷动态变化的最主要因素,这也验证了文献[8]的相关结论。
(2)基于监测平台CO2浓度数据和部分客流量实测数据,分别利用线性回归和神经网络两种算法建立动态客流量预测模型,并根据预测效果最终选择神经网络算法建立动态客流量预测模型,R2达到0.87,NRMSE=306人·h-1,预测模型能有效反映客流变化趋势。因此,对于新风量供给比较稳定的地铁车站,采用CO2浓度预测地铁车站客流量的方法是较为可靠的,该模型预测得到的客流量可应用于负荷预测。
(3)基于动态客流量预测模型,利用CO2浓度数据预测车站动态客流量,并将其作为车站负荷预测的输入参数。基于不同时间尺度历史数据,分别采用BPNN算法和SVM算法建立地铁车站空调负荷预测模型。比较两种模型在某一典型周(包含工作日和非工作日)的预测效果发现,两种算法的R2达到了0.95以上,RMSE均在70~90 kW之间,均表现出了良好的预测效果。但是SVM算法的运算时间是BPNN算法的3~4倍左右,故当数据量较大时推荐选择BPNN算法进行地铁车站的空调负荷预测。较高的预测效果也表明本文提出的方法能有效解决目前地铁车站负荷预测存在的问题,有较好的应用前景。
作者贡献声明:
苏醒:确定具体研究内容和实施方案,指导论文撰写及修改成稿。
王磊:完成数据整理分析及计算,撰写论文初稿。
田少宸:协助指导数据分析。
秦旭:提供现场数据,协助指导数据整理。

