基于HFSS和ADS仿真软件的频率选择表面教学探索

俞钰峰，程蒙蒙

（杭州电子科技大学电子信息学院，杭州 310018）

0 引言

电磁场与波是电子信息类专业本科生的专业基础课［1］。由于其概念抽象，涉及较多的公式和计算，多数学生在课程结束后对于电磁场的基本理论和概念依然无法熟练掌握。鉴于此，开设了微波技术前沿专题作为电磁场与波的后续课程。该课程通过对若干当前微波技术前沿领域的介绍和探究式学习，一方面让学生体验并实践科研训练，掌握科学研究的一般过程和方法；另一方面在实践过程中复习并巩固电磁场与波课程中所学到的电磁场的基本知识。在该课程中，选择了频率选择表面作为其中一个专题。频率选择表面（Frequency-selective surface，FSS）是一种二维周期性阵列，其对于入射的空间电磁波起到了滤波的作用，因此可视为一种空间滤波器［2-5］。频率选择表面有着广泛的应用，如隐身天线罩、电磁兼容等领域，因此一直是学术界和工程领域的研究热点［6-10］。

频率选择表面的研究涉及电磁波的传播、双端口微波网络、谐振器等电磁场和微波领域的基础概念。在分析方法方面，由于其既可以通过电磁场的角度进行分析，也可以构建电路模型，因此充分贯彻了“场路结合”的思想。基于以上原因，频率选择表面非常适合作为本课程的一个专题。在课程的教学中，为了避免传统微波与电磁场课程中内容抽象、公式繁杂的问题，在课程中引入电磁场仿真软件HFSS（High-Frequency Structure Simulator）和电路仿真软件ADS（Advanced Design System）。通过绘制电流或电场图，可有效帮助学生构建电磁场的物理图景；通过使用ADS与HFSS 对电路和电磁场仿真结果进行对比，可帮助学生构建起物理结构与电路模型之间的关联。

本课程以最基本的十字形带阻FSS 单元为例，通过对FSS物理模型与电路模型的分析和对比，使学生能够深入理解FSS的工作机理，同时有效掌握波的传播、双端口微波网络、谐振器等电磁场的基本概念。

1 频率选择表面概述

1.1 FSS的工作机理

从微观角度入手，FSS 工作机理可以理解为金属表面电子受激振荡，进而二次辐射，与入射电磁波叠加场的结果。假设空间某一平面上存在一根无限长的金属导线，其上有一个自由电子，如图1（a）所示。当入射电磁波从左侧垂直入射到金属导线上时，若此时电场方向与金属导线的方向一致，自由电子则会在电场力的作用下沿着电场方向在金属导线内振荡。入射波的一部分能量将被电子吸收用于维持振荡，而剩余能量将继续以电磁波的形式向右侧传播。直到入射波的频率达到某一特定值时，电磁波的能量将全部转化为电子的动能。此时，振荡的电子作为一个电偶极子将会向两侧辐射电磁波。其中，向左侧辐射的电磁波成为反射波，而向右侧辐射的电磁波将与入射波相互抵消，功率透过系数为零。这一现象即为谐振现象，此时电磁波的频率即为谐振频率［11］。当入射波的电场方向与金属导线方向垂直时，自由电子因被束缚难以在电场方向产生振荡，此时入射波将全部透过金属导线。从宏观角度来看，FSS 可分为偶极子阵列和缝隙阵列［12］。在偶极子情况下，金属贴片上激励起电流，金属贴片发生谐振；而在缝隙情况下，缝隙上激励起“磁流”，缝隙发生谐振［13］。

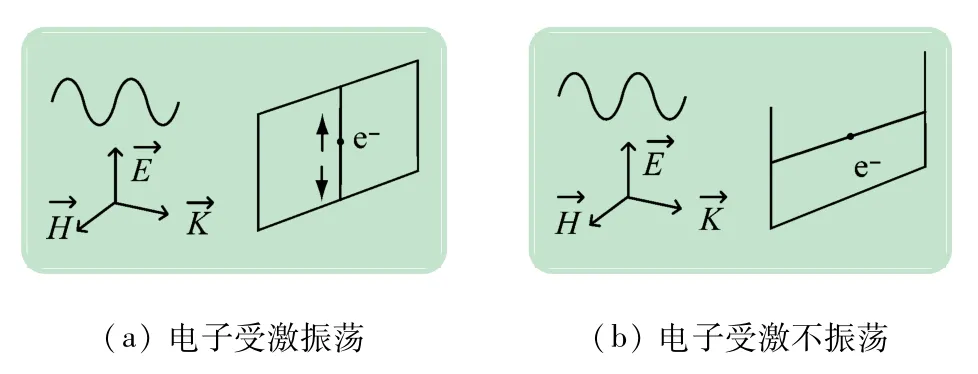
图1 电子振荡示意图

1.2 FSS的基本单元形式

对于不同结构的FSS单元，其金属表面（或缝隙）上电流（“磁流”）分布不同，进而FSS 的透波特性不同。根据透波特性，FSS 结构可分为带通型FSS 和带阻型FSS［14］。带通型FSS 又称孔径型FSS，由金属贴片的槽孔构成，带阻型FSS又称贴片型FSS，由金属贴片构成。FSS基本单元包括中心连接型、实心型、环型及组合型，如图2 所示。

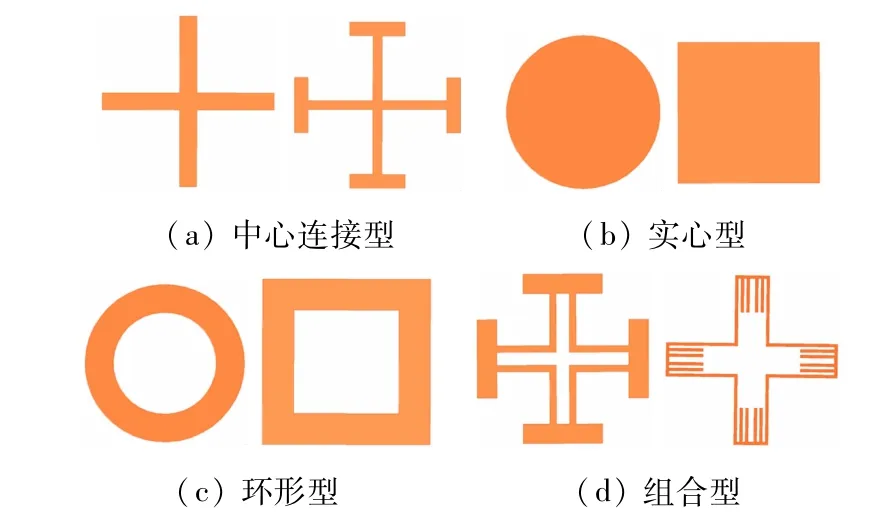
图2 FSS基本单元

1.3 FSS的基本性能参数

FSS通常是由金属贴片或金属片的槽孔按一定规律排列构成的平面周期结构［15］，以实现特定频率的反射或透射。一般用反射系数（）和透射系数（）来衡量反射和透射的程度。反射／透射系数分别定义为反射／透射电压与入射电压之比。一般以dB为单位，即

通常还会用带宽来衡量FSS在一定频段内保持阻带或者通带的能力，一般以-3 dB 作为临界值。对于带阻FSS，其带宽定义为≥-3 dB，即反射能量大于50%；对于带通FSS，其带宽定义为≥-3 dB，即透射能量大于50%。

考虑到本课程目的在于引导学生使用仿真软件进行初步的探究式学习，FSS的其他性能指标（例如衡量频率选择特性的矩形系数等）在本课程中暂不涉及。

2 基于HFSS和ADS的十字形单元特性分析

为了便于学生理解频率选择表面的工作机理，考虑到十字形单元结构简单，是FSS的基本单元形式，以十字形带阻单元为例，基于HFSS 和ADS 仿真软件对其进行电磁场和电路的仿真分析。在HFSS中，采用周期边界条件对FSS 的一个周期结构单元进行仿真，同时采用Floquet 端口作为激励。ADS 是电路仿真软件，可对十字形带阻单元等效电路进行计算和分析，可直观形象地展示各电路参数（如电感、电容等）对传输系数及反射系数的影响。

2.1 十字形带阻FSS单元及其等效电路模型构建

图3（a）所示给出了十字形带阻FSS 周期阵列的示意图，图3（b）所示为HFSS 中仿真模型。十字形是由两根沿着x方向和y方向的金属条交叠构成，它们分别对x和y极化的入射波产生响应。因此该结构可以对任意极化的入射波均有效。结构参数为b＝16 mm，Ld＝14 mm，w＝0.4 mm。在HFSS 中采用周期边界条件（沿着x和y方向的4 个面分别设置为Master和Slave boundary）对一个FSS 单元进行仿真，两个端口设置为Floquet Port，以此来模拟电磁波入射到无限大频率选择表面上的情景。

图3 十字形带阻FSS结构

金属条感应到电磁波时，其上电子产生振荡，因此可等效为电感；而两个相邻金属条之间的缝隙可等效为电容。因此十字带阻单元的二维周期阵列可被建模为串联L-C谐振电路，如图4 所示。其中的电路参数为L＝16.6 nH，C＝0.015 pF，Z0＝377 Ω。

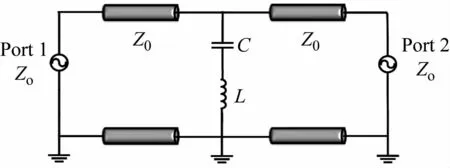
图4 十字形带阻FSS等效电路

2.2 HFSS和ADS软件计算及结果分析

用HFSS和ADS分别仿真了十字形带阻FSS的周期单元及其等效电路。仿真所得的反射和传输系数如图5 所示。可见，HFSS和ADS的结果非常吻合，这也验证了电路模型的准确性。该FSS阻带的中心频率f0为10.3 GHz，阻带（≥-3 dB）频段为9.25～11.4 GHz。

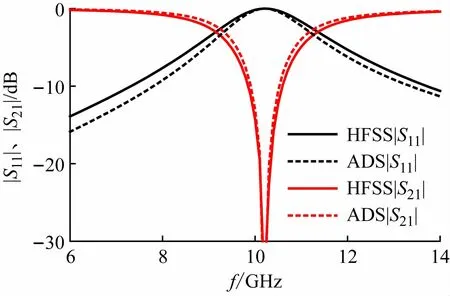
图5 反射系数及传输系数曲线图

为了直观地展示FSS 单元在阻带时的谐振特性，用HFSS仿真了FSS单元在阻带中心频率f0上一个周期（T）内4 个时刻（t＝0，t＝T／4，t＝T／2，t＝3T／4）的电流分布，如图6 所示。入射波电场方向沿y轴方向，因此仅有沿y轴放置的金属条上激励起振荡电流。该电流在末端为零，中间最大，呈现出典型的半波长分布，因此该带阻FSS 在阻带是一个半波长谐振器。为了验证谐振长度，可以计算在f0频点时金属条长度所对应的电尺寸为Ld／λ0＝0.48，与半波长非常接近。

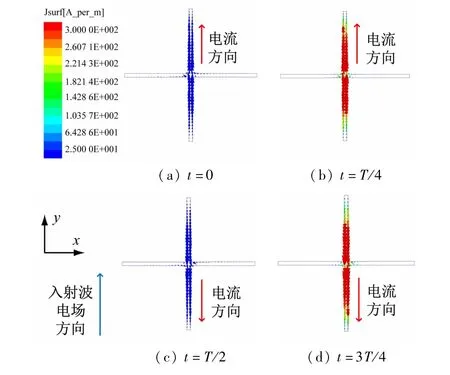
图6 FSS单元在阻带中心频率f0 的电流分布

按照半波长谐振器的观点，可以推断该FSS 的金属条长度Ld决定了阻带的中心频率f0，且Ld增大时f0应减小。为了验证此推断，同时也为该FSS 的设计提供指导，在HFSS 中使用参数扫描功能设置3 组Ld的长度进行仿真。图7 给出了Ld＝12、14 和16 mm时的传输系。可以很明显看到，当Ld＝12 mm时，f0＝12 GHz，当Ld增大时f0向低频移动。这与推断相符。

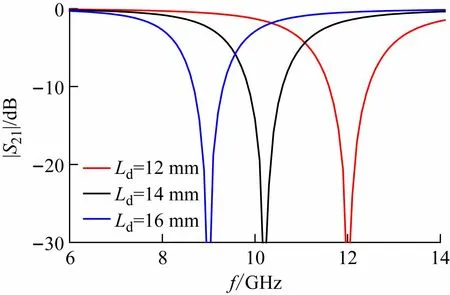
图7 不同金属条长度Ld 对应的

3 结语

将电磁场仿真软件HFSS及电路仿真软件ADS应用到频率选择表面专题的教学中，遵循“场路结合”的思想，同时进行场和电路的仿真与分析，并将抽象的概念形象化地展示，可以更好地帮助学生理解和掌握频率选择表面的原理。通过HFSS对电流和传输系数的分析，可使学生更清楚地了解频率选择表面的滤波原理。通过结果分析，可以更清楚地了解反射及透射系数的意义及其影响因素。这种将理论知识与仿真相结合的方式，提高了学生的学习积极性，扩充了课堂教学内容的丰富性，有效提高了课堂教学质量。