多元文化背景下新旧教材数学史料渗透情况分析



【摘 要】数学史作为数学文化的重要组成部分,是数学文化融入教学过程的主要表现形式,而教材作为传承数学知识和文化的重要载体,对中学数学教学起着重要的指导作用。研究者从历史起源和内容两个维度,分析多元文化背景下数学史在新旧教材中的渗透情况。结果表明,新旧教材史料基本一致,数学史来源比例过于悬殊,数学史应用水平较低。为此,研究者建议重视史料教育作用,增加史料引用数量;平衡不同起源史料,适应多元文化背景;提高史料应用水平,促进学生综合发展。
【关键词】多元文化;教材;数学史
【作者简介】林剑,中国人民解放军陆军特种作战学院助教,主要研究方向为数学教育。
一、引言
《普通高中数学课程标准(2017年版)》明确指出,教师应在教学活动中有意识地结合相应的教学内容,将数学文化渗透在日常教学中。数学史作为数学文化的重要组成部分,是数学文化融入教学过程的主要表现形式[1],而教材作为传承数学知识和文化的重要载体,对中学数学教学起着重要的指导作用。在多元文化背景下,为坚定文化自信,渗透数学文化,教材中数学史料的来源不应囿于单一区域或某一国家。因此,研究数学史在教材中的来源占比以及应用方式是否适应多元文化时代背景的要求具有重要意义。为了解目前教材中数学史的来源是否适应多元化社会的需求,其应用能否达到发展学生数学思维,培养学生情感、态度与价值观的目的。本研究从数学史的起源和应用两个维度出发[2],对数学史在人教A版新旧教材中的渗透情况进行对比分析。
二、数学史在新旧教材中的渗透情况比较
(一)比较维度
1.起源维度
数学的发展经历了初等数学时期、变量数学时期以及现代数学时期,其重心也进行了历次转移,形成了现今系统的数学知识体系。古代中国有着灿烂的数学文化,成书最迟在西汉的《九章算术》最早提到分数与盈不足等问题,《方程》章还在世界数学史上首次阐述了负数及其加减运算法则。成书于公元前1世纪的《周髀算经》最早记载了勾股定理的公式与证明及其在测量上的应用,以及怎样将它们应用到天文计算[3]。在16世纪初期,自然科学与工程的发展需求促使西方数学爆炸式发展,由几何原本奠定的公理化研究方法为西方数学取得较大突破,伴随着大航海时代全球经贸的扩张,使得西方数学乃至其他国家数学传入中国。多年来,中西方数学思想不断碰撞、融合,沉淀为如今的数学文化。因此,我国教材中数学史的引用主要有以下几个来源。
(1)中国数学史(CM)
中国数学始于先秦时期,其注重对实际问题的解释和再利用,形成以计算为核心的算法理论,具有浓郁的应用色彩[4]。在内容上多为对生活实践中遇到的问题进行归纳和理性的处理,强烈实用主义虽然促进了数学知識的传播,但同时也致使研究成果相对独立,未能深究背后的逻辑,并形成完备的数学体系。中国数学的特点奠定了中国数学史是以生活情境解释以及数学家事迹、成果为中心的历史。
由于近现代西方数学的发展,教材中大部分的公式、定理均源于西方数学,中国数学史的引用能让学生了解中国古代数学同样有着非凡的成就,能增强学生学好数学的信心,提升民族自豪感,坚定文化自信。此外,以生活情境解释以及数学家事迹、成果为中心的中国数学史更符合学生的认知规律,比较容易为学生所接受。
(2)西方数学史(WM)
与中国数学强调实用性不同,西方数学注重逻辑性,旨在建立统一理论以解释一切现象[5]。中西方数学的起源非常类似,但在经历相似时期后,西方数学取得蓬勃发展,得益于近现代西方数学沿用的是由几何原本奠定的公理化研究方法,其通过抽象符号将数学应用于实际问题中,进而形成高度抽象化的数学体系。
在人教版教材中,微积分、解析几何等数学内容模块均为西方数学研究成果,因此西方数学史是教材中数学史的重要组成部分。西方数学史的引用,一方面可以让学生了解异于中国的研究方法,培养学生的逻辑思维,另一方面可以开拓学生视野,促进学生综合素质的发展。
(3)多元文化数学史(MM)
多元文化数学史是指在不同文化背景下对同一问题的独立研究成果。数学史料“中外历史上的方程求解”,以时间顺序梳理了中外数学家关于方程解法的研究历程,介绍了中外对于低次方程式不同的解法,阐明了五次以上高次方程的根式解不存在。教材中多元文化数学史的引入,能使学生感受到中西方思维的差异,引导学生从不同角度思考问题,促进学生的思维发展。
(4)其他国家数学史(OM)
除西方数学史和中国古代数学史外,人教版教材的史料来源还涉及少数其他国家,如史料“弧度制发展史简介”就介绍了印度人曾用同一单位度量半径和圆周,是现知的最早的弧度制概念的雏形,这能帮助学生理解概念引入的意义。
2.应用维度
对教材中数学史的篇幅、栏目、内容进行文本比较、分析发现,数学史在教材中的应用存在差异,既有以提示框形式出现的数学家生平的介绍,也有以探究栏目引导的数学定理的推导证明。通过新旧教材数学史的分类归纳,依据对学生思维能力发展的促进程度不同,数学史的应用可分为以下四种类型。
(1)简单介绍(T1)
简短介绍某一数学家及其研究成果。这类数学史常以注释的形式出现,例如史料“第24届国际数学家大会会标”简短地介绍了该大会会标是根据中国古代的数学家赵爽的弦图设计的[6]。该史料引导学生通过观察图形各部分面积间的关系,使学生发现图形中的相等或不等关系,进而引入基本不等式的概念,激发学生的求知欲望。
(2)详尽介绍(T2)
详细介绍某种数学问题的解决方案,即某种算法或某一数学家的故事,但以结论的形式呈现,不对其探究过程或历史背景做深入阐述。这类数学史常以阅读与思考的形式出现,例如史料“中外历史上的方程求解”详尽地介绍了中外历史上关于方程的解法,以时间顺序还原了方程求解从低次向高次不断推进的过程,拓宽学生的视野。
(3)引领探究(T3)
介绍某种算法、概念或数学家的成果和结论,并解释其探究过程或文化背景,将数学产物与人物、历史背景、探究过程结合起来。这类数学史常以阅读与思考的形式出现,例如史料“三角学与天文学”将三角学伴随着天文学发展的起源与推广过程复现,使学生了解知识形成的历史背景及来龙去脉,帮助学生更好地理解知识。
(4)自主探究(T4)
介绍数学知识及其相关背景并提出问题,鼓励学生探究、推理或完成实验,在已有知识的基础上得出新的结论。这类数学史常以实习作业形式出现,例如史料“函数的形成与发展”要求学生以合作学习的方式进行探究,了解函数的发展历程与广泛应用,有效地培养学生的自主学习能力,让学生在自主探究中学习数学文化[7]。
(二)渗透情况
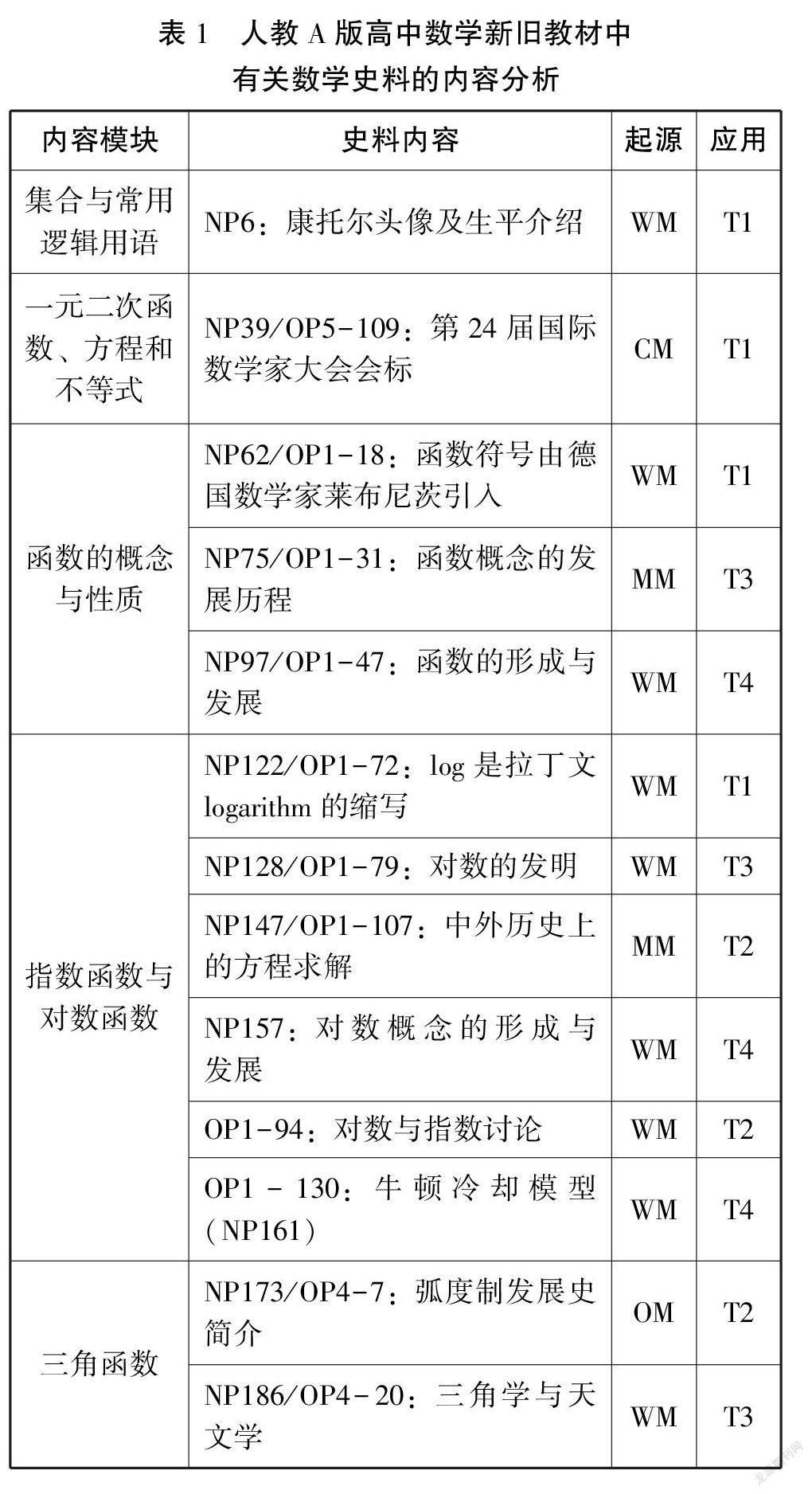
2019年人教A版高中数学新教材包括2册必修教材、3册选择性必修教材。本研究以人教A版必修一为例,对新旧教材共有内容的数学史渗透情况进行对比分析。新版教材必修一共包含“集合与常用逻辑用语”“一元二次函数、方程和不等式”“函数的概念与性质”“指数函数与对数函数”“三角函数”五章内容,对应旧版教材必修一全册、必修四第一章、必修五第三章内容模块。按照新版教材内容模块的顺序,从起源和应用两个对比维度对教材中的有关数学史料进行划分[8],其中“NP+页码”表示该史料内容在2019年人教版教材中的具体页码,“OP+册数+页码”则表示在2003年人教版教材中的具体册数及相应页码。
(三)对比分析
1.起源维度对比分析
从表1可知,新旧教材在数学史料选用上大部分一致,仅新增了“康托尔头像及生平介绍”“对数概念的形成与发展”,删除了2003年人教版教材中的“对数与指数讨论”,“牛顿冷却模型”不做史料解释,而是以例题的形式出现,新版教材总体上仍较多地以西方数学史作为史料的主要来源。以下对教材中的史料从起源维度进行分析(见表2)。
基于表1对新旧教材中不同起源的数学史进行分类汇总,可得到不同起源数学史在新旧教材中的总量直方图(如图1)。
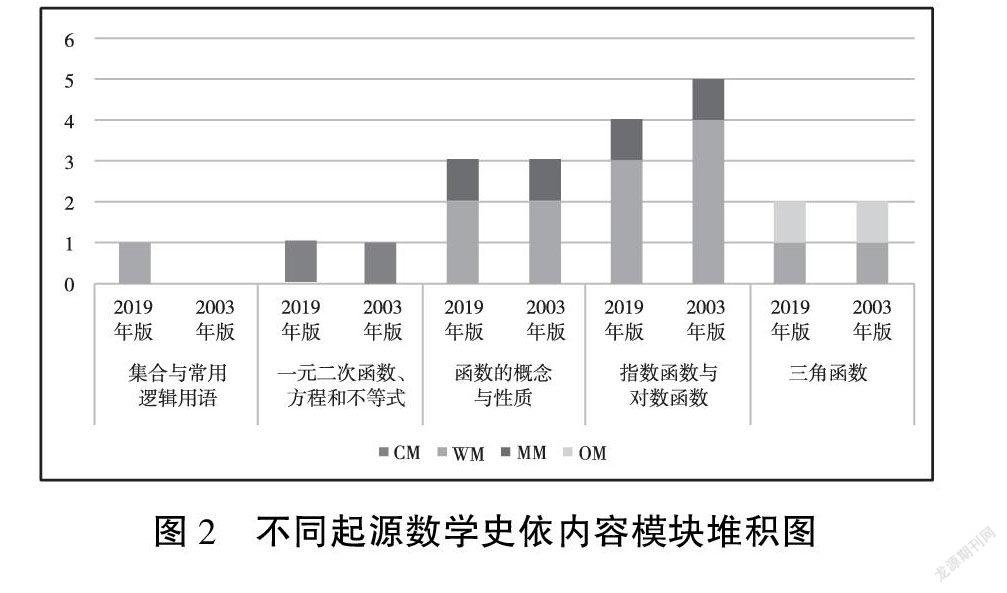
由图1可以看出,在必修一中四种不同起源的数学史均有引用,但西方数学史是必修一内容模块中数学史的主要来源,占该册数学史内容的63,中国数学史及其他国家数学史的引用比例相对较低。在图1中,由于内容模块间数学史数量的增减变化,新旧教材在不同起源维度的数量相等,对新旧版本教材数学史在起源维度上进行对比分析,依内容模块作图如下(如图2)。
由图2可知,新版教材在每一个内容模块中均有数学史,在数量分布上比旧版教材更为合理。新版教材相较于旧版教材在“集合与常用逻辑用语”中增加了一则西方数学史,而在“指数函数与对数函数”中减少了一则西方数学史。因此,在新旧教材中,数学史的引用总量相等。
2.应用维度对比分析
数学史不同的应用程度,对学生思维能力发展的促进程度也不同。新版教材对史料的运用偏向于简单介绍,以史料为背景进行引领探究和自主探究较少。以下对新旧教材史料的应用维度进行分析。
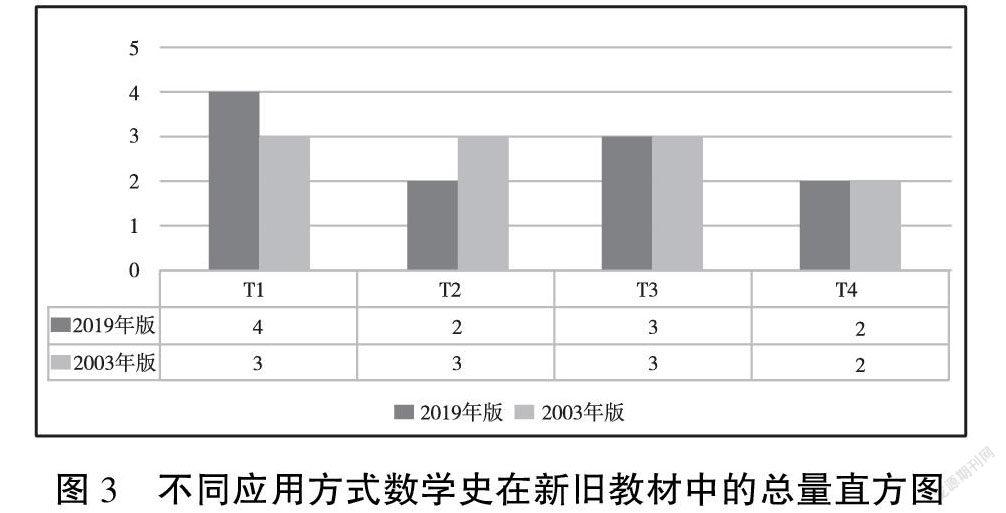
基于表3对新旧教材中不同应用方式的数学史进行分类汇总,可得到不同应用方式数学史在新旧教材中的总量直方图(如图3)。
由图3易知,新旧教材中数学史在T4维度的数量一致,但结合表1内容分析可知,新旧教材在T4维度的数学史料并不相同,新版教材新增了T4的方式应用史料“对数概念的形成与发展”,将原有的“牛顿冷却模型”不做史料解释,而是以例题形式出现。因此,新版教材相较于旧版教材在数学史的应用方式上有所提高。
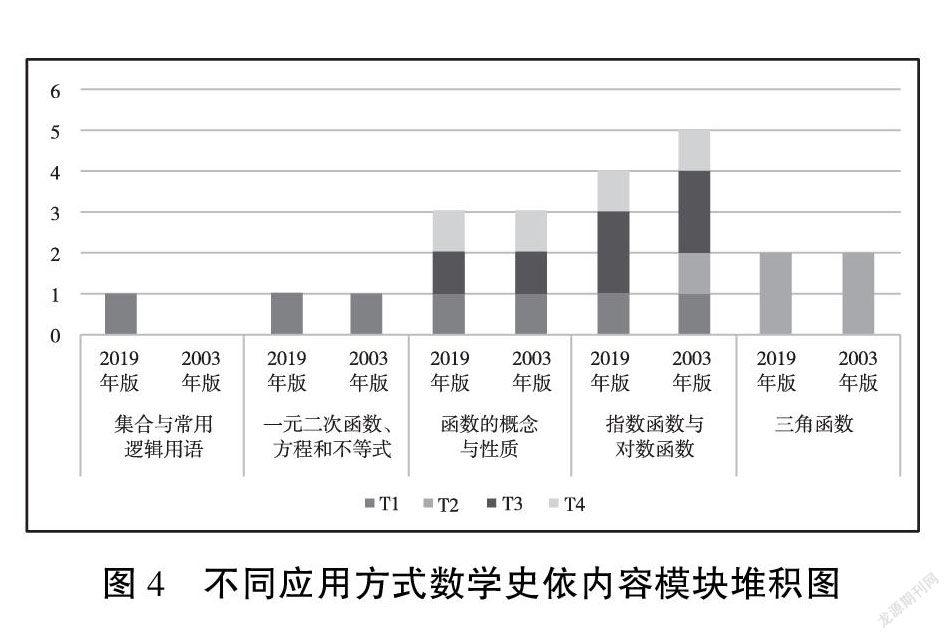
由图4可知,新旧教材中数学史在各内容模块中的应用方式均以介绍为主,引领学生探究或学生自主探究较少,仅在“函数的概念与性质”“指数函数与对数函数”章节中对数学的应用方式达T3及以上水平。
三、总结与反思
龐加莱认为,如果我们想要预见数学的将来,合适的途径是研究这门科学的历史和现状。数学史研究数学概念、数学方法和数学思想的起源与发展,及其与社会、经济和文化的联系。在多元文化的背景下,数学史的意义不再局限于激发学生学习兴趣,对于深刻认识数学体系与实现文化强国战略目标均具有重要的意义。
通过对新旧教材对比分析发现,数学史料基本相同,未进行大幅改动。教材中数学史的来源主要以西方数学史为主,中国数学史、多元文化数学史、其他国家数学史的数量均不足;教材中数学史的应用主要以介绍为主,旨在介绍某一数学家或其相关成果,对问题背景及演化过程的探究较少。因此,对于教材中数学史的编排,笔者建议可从以下三个方面进行改进。
(一)重视史料教育作用,增加史料引用数量
教材更新迭代工作烦琐复杂,因此教材不能实时更新,一套教材的沿用往往长达近十年时间,这就要求教材编写委员会应具有前瞻性。在依内容模块对新旧教材的数学史料对比分析后发现,新版教材的数学史料大部分沿用旧版教材的,仅对几处内容进行增减。旧版教材中数学史料无论在来源比例或是应用水平上均未完善。教材中数学史的引入不仅可以激发学生的学习兴趣,而且通过学习数学家研究治学的态度与精神能帮助学生形成正确的价值观,培养学生的思维。由此,笔者建议教材编写委员会应重视史料的人文与科学教育作用,增加教材中史料的引用数量,并适当对史料的来源比例及应用水平进行调整。
(二)平衡不同起源史料,适应多元文化背景
在多元文化的背景下,党的十九大提出坚定文化自信,推动社会主义文化繁荣兴盛,要求坚持不忘本来、吸收外来、面向未来。而在新旧教材中西方数学史均呈现出“一枝独秀”的态势。因此,平衡教材中不同起源的数学史料数量,特别是增加中国数学史的数量占比具有重要意义。随着外来文化的不断冲击,增加中国数学史的数量有利于学生了解中国古代数学的成就,提升民族自豪感,坚定文化自信。此外,适当增加多元文化数学史及其他国家数学史,能更好地培养学生适应多元文化的综合能力。多元文化数学史强调一个数学问题在中西方甚至更多其他国家中的研究历史,让学生感受解题逻辑背后的异同,培养学生的发散性思维。其他国家数学史的引入旨在帮助学生理解概念的形成与发展过程,开拓学生的视野[9]。
(三)提高史料应用水平,促进学生综合发展
学习数学的目的在于培养学生的逻辑推理能力,依据对学生思维能力发展的促进程度不同,数学史的应用情况可分为简单介绍(T1)、详尽介绍(T2)、引领探究(T3)、自主探究(T4)。在新旧教材中史料多以介绍形式呈现,以史料为背景引领学生探究或鼓励自主探究较少,不利于学生逻辑推理数学核心素养的培养。笔者建议将T1类型数学史改进为T3、T4类型的数学史,充分发挥在多元文化背景下数学史料的作用,鼓励教师结合历史背景解释数学成果的探究过程。为照顾一些基础薄弱、探究和创新能力不足的学生的学习发展需要,T4的数量应略少于T3。同时,提高数学史料的应用水平,在传递数学史的人文价值的同时发展学生逻辑推理能力,促进学生综合能力的发展。
参考文献:
[1]蒲淑萍,汪晓勤.教材中的数学史:目标、内容、方式与质量标准研究[J].课程.教材.教法,2015(3):53-57.
[2]张维忠,孙庆括.多元文化视角下的初中数学教科书比较[J].数学教育学报,2012(2):44-48.
[3]张国定.数学史融入数学教学的实践研究[D].兰州:西北师范大学,2007.
[4]孟梦,李铁安.“问题化”:数学“史学形态”转化为“教育形态”的实践路径[J].数学教育学报,2018(3):72-75.
[5]唐恒钧,张维忠.国外数学课程中的多元文化观点及其启示[J].课程.教材.教法,2014(4):120-123.
[6]张维忠,马俊海.我国初中数学教科书中的数学史及其启示[J].当代教育与文化,2018(6):56-60.
[7]王红.数学史与数学教学的结合:问题与路径[J].当代教育科学,2014(16):63-64.
[8]高岩,周畅,段耀勇.论数学史的多维向度[J].广西民族大学学报(自然科学版),2012(3):23-26,88.
[9]路梦绮,林剑,周莹.多元文化背景下数学史在教科书中的渗透情况分析[J].中小学课堂教学研究,2019(1):21-25.
(责任编辑:陆顺演)

