尺规作图教学重在“探索方法”
钱德春 于婷婷


摘要:教学要求的变化和学生能力的不足都表明,尺规作图教学重在引导学生探索作图方法。为此,需要细化尺规作图的教学过程:面对作图问题(任务),引导学生执果索因,感悟解题思路;引导学生追根溯源,寻找作图方法;引导学生变式作图,强化思路与方法;引导学生多维感悟,把握尺规作图的本质。
关键词:尺规作图;作图方法;探索
尺规作图是有限次地使用无刻度的直尺和圆规作图的活动,是初中数学教学的重要内容。本文基于课标对尺规作图教学要求的变化和一道中考尺规作图题的考查,给出尺规作图教学的几点建议。
一、教学要求的变化:从“了解作图方法”到“探索作图方法”
《全日制义务教育数学课程标准(实验稿)》对尺规作图内容教学的一般要求是“了解尺规作图的步骤,对于尺规作图题,会写已知、求作和作法(不要求证明)”。《义务教育数学课程标准(2011年版)》对尺规作图内容教学的一般要求是“了解作图的道理,保留作图的痕迹,不要求写出作法”。据了解,即将颁布的新版义务教育数学课程标准对尺规作图内容教学的一般要求是“经历尺规作图的过程,增强动手能力,能够想象出通过尺规作图的操作形成的图形,理解尺规作图的基本原理与方法,发展空间观念和空间想象力”。
从了解作图方法(步骤),到理解作图道理(原理),再到探索(发现)作图方法(步骤),课标对尺规作图内容教学的要求越来越高:一般来说,探索结论比证明结论难度大,证明结论比了解结论难度大。
究其原因,可能是,仅仅将尺规作图作为技能,单纯记住作图方法的价值已经不大了,因为借助更先进的工具(包括电脑作图软件等),作图可以变得更加容易;而通过探索发现作图方法(同时可以理解作图道理)的过程,是执果索因(先想象出通过尺规作图的操作形成的图形),利用几何知识解决几何问题的过程,可以更好地培养学生的探索性思维(包括直觉思维、发散思维、联想思维等)和直观想象能力、逻辑推理能力。郑艳,石树伟.初中尺规作图教学谈——从一道限定工具作图题说起[J].教育研究与评论(中学教育教学),2021(4):5053。
此外,新版课标不再有“不要求写出作法”的表述,可能是因为关注到写出作法可以培养学生的数学语言表达能力,以及图形、文字与符号语言转换能力。
二、学生探索作图方法的能力不足——从一道中考题说起
2021年泰州市中考卷中有一道限制工具使用次数的尺规作图题:
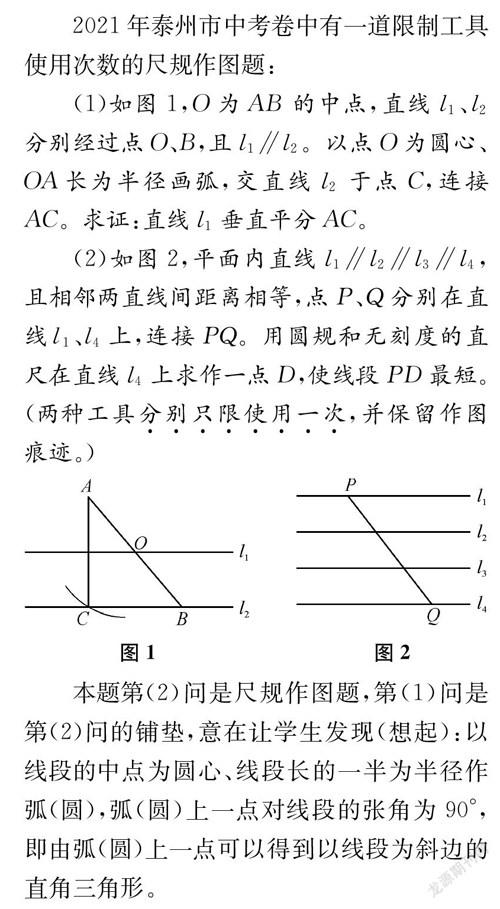
(1)如图1,O为AB的中点,直线l1、l2分别经过点O、B,且l1∥l2。以点O为圆心、OA長为半径画弧,交直线l2于点C,连接AC。求证:直线l1垂直平分AC。
(2)如图2,平面内直线l1∥l2∥l3∥l4,且相邻两直线间距离相等,点P、Q分别在直线l1、l4上,连接PQ。用圆规和无刻度的直尺在直线l4上求作一点D,使线段PD最短。(两种工具分别只限使用一次,并保留作图痕迹。)
本题第(2)问是尺规作图题,第(1)问是第(2)问的铺垫,意在让学生发现(想起):以线段的中点为圆心、线段长的一半为半径作弧(圆),弧(圆)上一点对线段的张角为90°,即由弧(圆)上一点可以得到以线段为斜边的直角三角形。
有了第(1)问的铺垫,第(2)问的解决并不太难:
显然,由于点P确定,直线l4确定,要在直线l4上确定一点D,使线段PD最短,只要PD⊥直线l4即可。受第(1)问的启发,可先确定PQ的中点,再以该中点为圆心、PQ长的一半为半径作弧,与直线l4相交得到点D。但是,由于题目条件规定直尺和圆规“分别只限使用一次”,因此,无法确定PQ的中点。这时,可以结合题中平行线的条件,转换思路:通过PD垂直于其他直线,得到PD⊥直线l4。显然,图中确定了PQ与直线l2、l3的交点,可分别设为点G、H,则G为PH的中点。由此,可以点G为圆心、PG长为半径作弧,与直线l3相交得到点E,延长PE,与直线l4相交得到点D。这样,就有PE⊥直线l3,PD⊥直线l4。
但是,本题第(2)问的考试结果不太理想:得分率仅为0.298。其原因主要有两个:一是学生对“分别只限使用一次”的作图要求不知道如何处理;二是学生机械套用第(1)问的结论,只考虑作PQ的中点,没有想到将“PD⊥直线l4”转化。
这在一定程度上反映了在《义务教育数学课程标准(2011年版)》没有明确提出“探索作图方法”要求的背景下,教师对尺规作图内容教学(以及教材对尺规作图内容编写)的定位及策略不够清晰与合理:通常直接呈现作图方法,有时追问作图道理,没有很好地引导学生探索发现作图方法,没有解决作图方法“从哪儿来”“是怎么想到的”的问题,使学生“一知半解”,只会“机械模仿”,尤其是遇到有一定思维含量的作图问题时不会展开探索。
三、尺规作图教学的几点建议
教学要求的变化和学生能力的不足都表明,尺规作图教学重在引导学生探索作图方法。为此,我们认为,需要细化尺规作图的教学,使之成为一个循序渐进的过程。作图方法本质上是由作图问题(任务)引发的知识,下面主要以上述作图问题为例,说明如何细化尺规作图的教学过程。
(一)引导学生执果索因,感悟解题思路
解决尺规作图问题的基本思路是“倒过来想”,即假设图形已经作出,再根据想象的图形分析需要满足什么条件,什么条件是可以通过直尺和圆规的作图得到的。教学中,教师要多问学生“我要什么图形”“已经有什么条件”“还需要什么”“怎么得到”。例如,上述作图问题的教学中,教师要引导学生思考:要使线段PD最短,需要什么条件?并让学生逐步认识到,这是探索作图方法的出发点,执果索因是探索作图方法的基本思路。
(二)引导学生追根溯源,寻找作图方法
数学问题千变万化,却不离其宗。尺规作图教学中,学生明确“从作图结果出发,执果索因”后,教师要善于引导学生追根溯源获得灵感,寻找作图方法。
一是从基础知识中寻找灵感。解决尺规作图问题的基础是几何知识,教师要引导学生从基础几何知识出发获得灵感。例如,解决上述作图问题的关键是如何得到垂直或直角。教学中,可以启发学生回忆与垂直或直角有关的知识,如“一条直线垂直于平行线中的一条,必然垂直于另一条”“等腰三角形底边上的中线就是底边上的高”“一边上的中线等于这边长一半的三角形是直角三角形”“圆中直径或半圆所对的圆周角是直角”等。得到这些有关垂直或直角的定理(结论),就为解决上述作图问题提供了灵感。
二是从基本问题(已有问题)中寻找灵感。除了联想基础几何知识,加强对基本几何问题与图形的识别与联想,也有利于打开思路获得灵感,让学生自然生成作图方法。例如,上述作图问题的图形及结论在苏科版初中教学教材中有3处原型:
一是八年级上册《2.5 等腰三角形的轴对称性》的例2:“如图3,∠EAC是△ABC的外角,AD平分∠EAC,AD∥BC。求证:AB=AC。”
二是九年级上册《2.2 圆的轴对称性》习题的第4题:“如图4,AB、CD是⊙O的直径,弦CE∥AB,CE=40°,求∠AOC的度数。”
三是九年级上册《2.4 圆周角》练习的第2题:“如图5,AB、CD是⊙O的直径,弦CE∥AB,BD=BE吗?为什么?”
由这些问题,学生也有可能想到上述作图问题的作图方法。
(三)引导学生变式作图,强化思路与方法
变式教学是指通过问题的“形变神不变”和“神变形不变”,在内化基本思路与方法的同时,培养学生的聚合思维与发散思维能力。得到作图方法后(当然,需要有序表达方法、证明检验方法,但这基本上可以与探索过程同步进行),教师要充分利用作图问题的发展价值,适度开展尺规作图的变式教学(如将问题纵向变式,向纵深发展;或将问题横向变式,与其他领域的知识结合),从而让学生对解题思路的理解和对作图方法的认识得到升华。
例如,对上述作图问题可以作如下变式:
变式1如图6,平面内直线l1∥l2∥l3∥l4,且相邻两直线间距离之比为1∶2∶3,点P、Q分别在直线l1、l4上,连接PQ。用圆规和无刻度的直尺在直线l4上求作一点D,使线段PD最短。(两种工具分别只限使用一次,并保留作图痕迹。)
这是一种纵向变式,将原来“相邻两直线间距离相等”的条件适度一般化,需要学生将适度一般化的情形向原来的特殊情形转化(这里给的数据比较特殊,1+2=3,因此,其中一个分点就是PQ的中点),可以帮助学生充分体会解决尺规作图问题乃至一般数学问题时极其重要的转化与化归思想。
变式2如图7,平面内直线l1∥l2∥l3∥l4,且相邻两直线间距离相等,点P在直线l1上,点G、Q分别在直线l4上,分别连接PG、PQ。用圆规和无刻度的直尺在PQ上求作一点D,使线段GD平分△PGQ的面积。(两种工具分别只限使用一次,并保留作图痕迹。)
这是一种横向变式,将原题与三角形的面积相联系。如何处理“线段GD平分△PGQ的面积”?先要认识到D为PQ的中点,然后需要从中心对称的角度思考:“平行”加“相等”可得平行四边形,因此,可以根据平行四边形的对角线互相平分来作图。
此外,这里的变式还可以体现在作图工具的进一步开放与限制上,比如,不限制作图工具或限制作图工具的使用次数和种类,完成同样的作图,从而让学生进一步领悟如何展开探索。
(四)引导学生多维感悟,把握尺规作图的本质
启发学生感悟数学本质、掌握通性通法是数学教学的最高境界。
尺規作图教学要让学生感悟作图方法的本质是“交轨”。尺规作图所作图形无论多么复杂,都离不开关键点位置的确定,而点的位置是由线与线相交得到的,这些线的本质是满足特定条件的点的轨迹。初中阶段的轨迹主要是直线与圆弧。教学中,“交轨法”的名称不必提出,但要通过具体案例引导学生初步感知“交轨法”的意义。
尺规作图教学要让学生感悟作图问题之间的联系性和一致性。比如,作线段的垂直平分线、过一点作已知直线的垂线、作已知角的平分线,这3种作图问题的本质都是构造轴对称图形。
尺规作图教学还要让学生感悟直观、操作与推理的相互依存关系。作图之前要先假设图形已经作出,由此寻找作图方法,那么,作出的图形是什么样子的,这就需要直观想象。知道了作图方法,如何准确地作出图形,这就需要动手操作。图形作出之后,要弄清为什么这样作、这样作对不对,这说明尺规作图是建立在逻辑推理基础上的。

