聚类分析和判别分析视角下社保重仓股企业财务指标有效性

谢凯南

一、引言

（一）研究背景及意义

2001年起，国务院决定在辽宁省启动个人社保账户试点，将个人缴费工资中占比8%的部分记入个人账户。截至2005年底，以辽宁一个省为例，就已经累积落实个人账户资金201亿元。随着上述政策在辽宁落地，国务院决定将试点扩大至吉林、黑龙江、天津、山西、上海、江苏、浙江、山东等13个省份。截至2009年底，以上开展试点的各个省份共积累基本社会养老保险个人账户资金达1 569亿元。随着个人账户的费用积累逐步增加，社会养老保险个人账户基金的资金规模也同步累积扩大。面对人口老龄化条件下养老金支付危机，仅仅依靠现有“存银行，买国债”的投资渠道已不能满足基金保值增值的要求，这就促使社会养老保险个人账户基金迫切需要拓宽投资渠道，入市投资已成为必然趋势。

社会养老保险个人账户基金入市后，对股票价格产生影响的，除了财政、货币、产业等宏观经济因素外，同时还有财务数据、整体市场预期等微观因素。在以上因素中，公司对外公布的财务信息能够直接或频繁引用，因此企业财务信息是股票市场信息的主要来源，也是投资决策的重要基础。鉴于此，本文运用SAS软件，选取反映企业基本情况的财务指标，对公司进行基本面分析。

（二）数据筛选

本文以社保基金重仓股为研究对象，从2011年社保基金一零一至一零八共8个重仓股组合中，每个组合随机抽取5只股票，包含轴研科技、辽通化工等共40只股票即40家上市公司作为研究样本。对于样本企业，本文将从三个角度来分析其基本面情况，包括盈利能力、偿债能力及成长能力，能够较为全面客观地评价企业的发展现状。其中，评价盈利能力的指标主要包含每股收益、净资产收益率，评价偿债能力的指标主要包含资产负债率、股东权益比率，评价成长能力的指标主要包含净利润增长率、主营业务增长率。选取的各财务指标数据来自和讯网，均为企业2011年前三季度的财务报告数据。

二、聚类分析

（一）类平均聚类方法

1.数据的均方根。

本文研究的样本为轴研科技、辽通化工等40只社保重仓股，即共有40家沪深证券交易所上市的企业，故各个企业之间的距离有=780个，距离的均方根为4.03。该方法下共有39次聚类，每一类的企业数目从2到40不等。

2.伪F统计量。

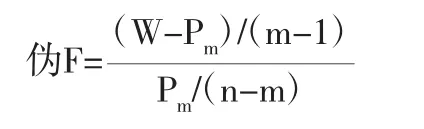
伪F统计量用于评价分为m类的聚类效果。伪F统计量数值越大，表明越可显著地将n个样品区分为m个类。伪F统计量可以作为确定类个数的有用指标。在本例中，第一次聚类两者之间的标准化欧几里得距离最小，伪F统计量最大值为184，而最后一次聚类的伪F统计量最小为29.1。

3.伪t2统计量。

其中D2KL=WM-WK-WL即为合并类GK和GL合并为新类GM后类内离差平方和的增量。伪t2统计量用来评价合并类GK和GL的效果。伪t2统计量值大表示GK和GL合并为新类GM后，类内离差平方和的增量L相对于原GK和GL的类内离差平方和大，这表示被合并的两个类GK和GL是分得很开的，也即表明上一次聚类的分析结论是好的。伪t2统计量是确定类个数的有用指标。本例中，第一次聚类是康力电梯（002367）和通鼎光电（002491）归为一类，两者之间的标准化欧几里得距离最小，伪t2最小。以此类推，最后一次聚类是第2聚类和第3聚类形成了最大的聚类，两者之间的标准化欧几里得距离最大，伪t2最大，伪t2为43.7。

类平均聚类方法的统计量与重心聚类方法、最短距离聚类方法相同，这里不重复描述。类平均聚类方法、最短距离聚类方法以及重心聚类方法三种谱系聚类分析的结论图分别如图1、图2和图3所示。

图1 类平均聚类方法的谱系聚类图

图2 最短距离聚类方法的谱系聚类图

图3 重心聚类方法的谱系聚类图

（二）离差平方和（Ward）聚类法

1.协方差矩阵特征值（见图4）。

图4 离差平方和聚类方法的谱系聚类图

在本文中特征值为：Eigenvalue=[1099.44…1485.95…1095.96…162.30…112.05…4.55…0.14]T，其中第一类特征值为11099.44，它与后面6个特征值相差悬殊，第一特征值占总方差的79.51%。因此，第一聚类是主要的聚类。

2.复相关系数R2统计量。

3.半偏R2统计量。

该统计量用以评价合并GK和GL的效果。半偏R2统计量是上一步R2值与该步R2值的差，因此半偏R2统计量数值越小，上一次聚类的效果更加优秀。本例中第一次聚类半偏R2统计量最小为0.0001，聚类效果较好；最后一次聚类半偏R2统计量为0.5346，聚类效果最差。

（三）结论

从这四种聚类法的树形图可以看出，可以把这40家社保重仓股企业分为两类，其中三友化工（600409）、中环股份（002129）、广东明珠（600382）、凯迪电力（000939）为第一类，其余36家企业为第二类。

三、判别分析

判别分析主要解决的问题是在已知根据过往经验运用某些方法已把需要研究的样品分为若干组的情况下，来判定新的观察样品应该归属的组别。基于上面6项财务指标的聚类分析，我们已经将社保重仓股中的40家企业分为两大类。现在，我们从其他的社保重仓股中随机抽出10只股票，采用判别分析方法分析这10家企业分别属于哪一类别。

随机抽取的股票如下：辰州矿业（002155）、国统股份（002205）、华东电脑（600850）、沈阳机床（000410）、西宁特钢（600117）、晨光生物（300138）、伊利股份（600887）、辽通化工（000059）、华斯股份（002494）、津劝业（600821）。

（一）一般线性判别

1.分组水平信息。

我们可以得到分组变量的值：两种类型。各组的频数依次为：4、36。各组的权重依次为：4、36。各组在全部样本中所占的比例分别为：0.1、0.9。同时，各组先验概率分别为0.5。分组水平信息如图5所示。

图5 分组水平信息

2.联合协方差矩阵信息。

协方差矩阵的秩为6；协方差矩阵行列式的自然对数ln（∑）=26.90464。

3.组间广义平方距离。

图6 组间广义平方距离

4.线性判别函数。

Func1=-499.34001+0.18588X1+7.24876X2+10.39264X3+10.85249X4-0.13626X5-0.04560X6

Func2=-552.86473+0.01611X1+13.66601X2+11.09873X3+11.59233X4-0.09153X5-0.16237X65

回代结果根据该部分判别到各组的观察值及其所占百分比、各组误判观测值的估计得出，以下是SAS得到的回代结果（见图7图8）。

图7 各组别误判观测值估计结果

图8 新样本组别判别结果

SAS运行结果显示，不存在各组中某个观察值被误判的情况，说明该判别的可信度很高。

5.前瞻性检验。

前瞻性预测采取一般线性判别函数的交叉实证进行结果置换。我们将10家上市公司的财务比率数据代入判别函数和贝叶斯（Bayes）判别公式，即将10家公司分别归为各自的组别。

SAS运行结果表明，社保重仓股企业辰州矿业（002155）被判为第1类别，其余9家企业国统股份（002205）、华东电脑（600850）、沈阳机床（000410）、西宁特钢（600117）、晨光生物（300138）、伊利股份（600887）、辽通化工（000059）、华斯股份（002494）、津劝业（600821）均被判为第2类别。

（二）典型判别

1.多变量统计量和F值。

对数据进行SAS运行后的结果如图9所示。

图9 多变量统计结果

由结果可知，我们得到：

Wilk’s Lambda=0.2292，F-Value=18.50，P-Value＜0.001，拒绝原假设。同理，Pilla’s Trace，Hotelling-Lawley Trace，Roy’s Greatest Root这三个统计量都拒绝原假设，应用典型判别的可信度很高。

2.E－1B的特征值：典型相关系数数值是0.87797，特征值数值是3.3636。

3.典型判别函数。

SAS输出了原始典型变量系数，如图10所示。

图10 原始典型变量系数

即典型变量和原始变量的关系表示为：Z=0.028491899X1-1.076976938X2-0.118500147X3-0.124164041X4-0.007505769X5+0.019597028X6+C将各变量的组均值代入上式，即可得出C的值。

（三）结论

典型变量Z作为原始变量的线性组合，已经能够囊括原始变量的大量信息，且同时兼顾概括各组别之间的差异。典型判别是一种很好的降维技术，它用效率的典型变量代替原始变量，把样本分组情况直观表现出来。本例中，我们将社保重仓股的40家上市企业分成了两大类别，然后对各个类别中企业的财务数据进行分析，可以依次将这两大类企业区分为基本面良好和较差两种类别。这样就能够对企业的基本面信息做出正确判断。