一种基于ANSYS Workbench 的环形灌装缸有限元分析

黄文金 孙敬慧 周波

随着灌装行业的飞速发展，行业竞争越来越激烈，同时消费者对食品卫生也越来越重视，对灌装机械有了更高的要求，从而促使食品机械设备生产厂家在机械设备的改进和研发上投入更多的人力、财力和物力。

灌装缸是一种用来存储物料的容器，与气液分配相连。物料通过分配器进入到灌装阀内进行灌装，并定量进入瓶内。传统灌装缸是截面为矩形的普通灌装缸，如图1 所示。这种灌装缸成本高昂，制作复杂，工艺要求高，且清洗不易。由于食品行业的特殊性，产品的卫生标准要求很高，对灌装缸的清洗较为频繁，清洗时费时费力，对生产有较大的影响。现设计了一种环形缸，如图2 所示，这种灌装缸截面为圆形，用料节省，工艺简单，方便清洗，质量小，成本较普通缸大幅下降。

图一 传统普通灌装缸

图二 新型环形缸

1.环形缸的结构

如图三所示，环缸（1）固定到安装盘（4）上。环缸均布焊接8 个连接块（2），立柱（3）一端与连接块相连，一端与安装盘相连。

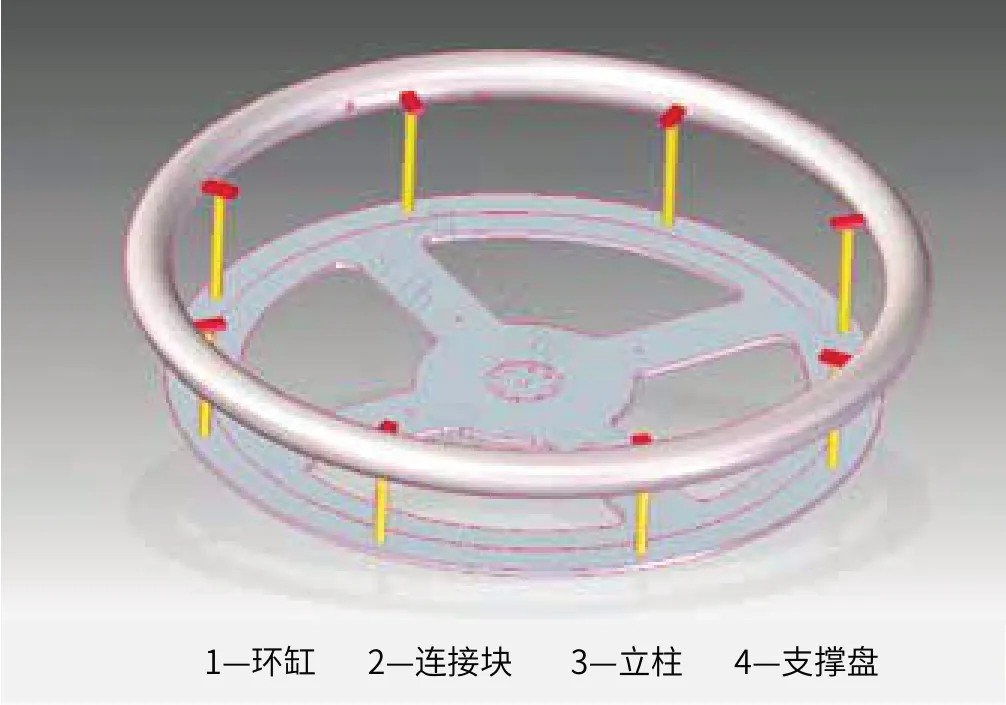
图三 环缸的主要结构图

2、环形灌装缸的强度分析

用三维软件Solidedge 绘制三维模型，去除灌装缸上的小特征，简化结构后，导入ANSYS Workbench 中。灌装缸部件的各结构材料为304 不锈钢，密度为7.93 g/cm3，304 的弹性模量为194GPa，泊松比为0.3，屈服强度为205MPa。

设定网格尺寸，划分自由网格共650149 个，平均网格质量为0.783，如图四所示。

图四 划分网格

支撑盘安装在缸支架上，现用固定约束；环缸内装满液体，施加0.6MPa 的水压，整个装置在标准大气压下工作，施加一个标准地球重力，如图五所示。

图五 载荷和约束

分析后从应力云图和位移云图可以看到，最大应力为49.196MPa＜205MPa，最大位移为0.165mm，最大应力和最大位移在灌装缸开孔较多的一侧，如图六所示。该结构强度足够，设计合理。

图六 位移云图

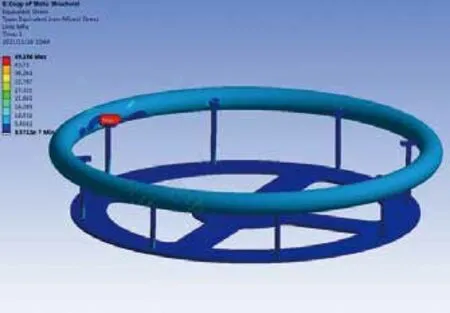
图七 应力云图

3、环形灌装缸的模态分析

动力学的通用运动方程为：

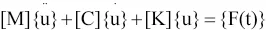
其中：M 为质量矩阵，C 为阻尼矩阵，K 为刚度矩阵，F 为外载荷，为加速度向量，为速度向量为位移向量。

式5-7 可以表达多种分析类型，对模态分析而言，因模态是机械结构的固有振动特性，与外部的激励无关，即，其方程可以写为：

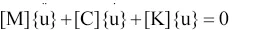
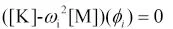
由式5-9 可求得广义的特征值和特征向量，也就是动力系统的振型和固有频率。令，有：

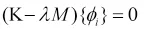
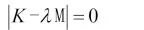
在workbench Mechnical 模块中求解上述方程时，是在一定的假设条件下求解的，即K 和M 是常量，同时满足以下条件：

A、假设材料是线弹性材料。

B、使用小挠度理论，不包含非线性特征。

C、不包含阻尼。

D、假设结构没有激励。

模态分析按是否对物体进行约束分为约束模态和自由模态分析两种情况。这两种模态分都无需施加载荷，其中前者需要约束边界条件，后者不需要约束。本文采用约束模态分析，分析的步骤和流程与静力学分析大致相同。

建立模型，设置好材料属性、划分网格后，设置分析项，设定模态数是6，频率0HZ--108Hz。

默认坐标系为约束坐标系，灌装缸的回转中心设置为与坐标原点重合。约束立柱沿X、Y、Z 轴方向的移动自由度，以及XZ、YZ 方向的转动自由度。

经分析后，得灌装缸前6 阶的模态分析结果图，如图八所示。

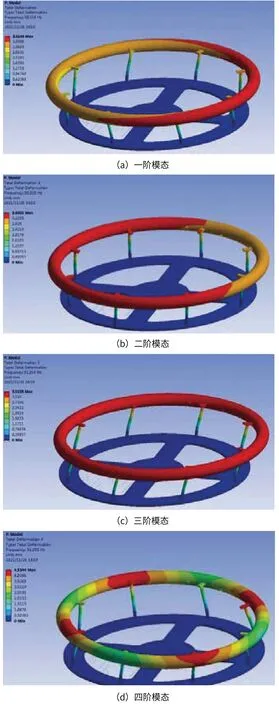
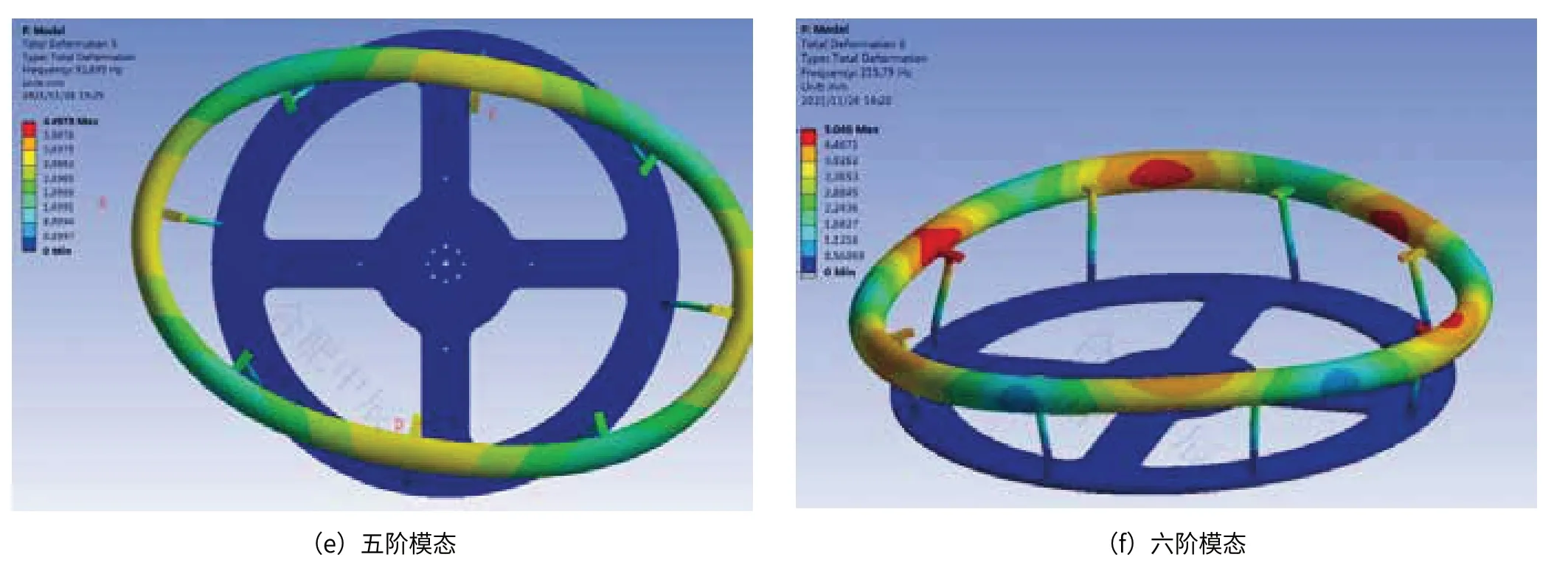
图八 模态分析结果图

从图八的分析结果可以看出，一阶模态变形绕着z 轴反复旋转；二阶模态在X0Z 平面内摇摆，；三阶模态在ZOY 平面内摇摆；四阶和五阶是在XOY 平面内扭转；六阶模态是四阶和五阶的叠加，XOY 平面内扭转。

图中的六阶模态的固有频率在表1 中列出。

表1 1-6 阶固有频率

上文中已确定灌装机的转速为5r/min，转频率为0.0833HZ，和其固有频率相差相差较大，灌装缸不会发生共振，满足设计要求。

4、结论

通过solidedge 建立模型，将其导入ANSYS Workbench中，计算得到新型环状缸的最大应力，环状缸结构在水压0.6MPa 时，最大应力为49.196MPa 远小于304 不锈钢的屈服极限。模态分析计算的结果得到，在灌装机正常工作时的转速远小于灌装缸结构的固有频率，所以灌装缸不会发生共振，设计合格。