一种可工程化检测磷酸铁锂电池问题的方法

赵尚玉，张 震，王宝源，曾驱虎

（深圳市科陆电子科技股份有限公司，广东 深圳 518000）

随着全球气候变暖问题日益严重，目前世界上大多数国家均提出碳中和[1]目标。根据Climate News，当前多达28个国家提出本国的碳中和目标以及完成的时间节点，其中中国在2020 年9 月的第75届联合国大会上进一步明确2030年前实现碳达峰[2]、2060 年前达到碳中和的目标。王峰等[3]提出实现碳中和的关键是转换能源结构，提升非化石能源的发电比例。

目前已经广泛应用于商业化的电化学储能技术主要为铅蓄电池和锂离子电池，其中锂离子电池累计装机规模最大，2020 年底全球锂离子电池累计装机规模已达13.1 GW，占电化学储能总规模的92%[4]。同时，锂离子电池的成本在不断下降，2020 年锂离子电池市场平均成本仅为137 USD/kW·h，近10年下降幅度高达88%，随着成本的逐渐下降以及储能相关政策的出台，储能系统应用将进一步扩大。储能领域目前主要使用磷酸铁锂(LiFePO4)电池，其占比超过94%[5]，主要应用在电网侧、电源侧和用户侧等领域。

随着LiFePO4电池大规模应用于储能，如何及时检验出LiFePO4电池使用过程中出现的问题逐渐被提上日程。冯祥明等[6]提出影响锂离子电池安全的因素包括针刺、短路、挤压、热冲击、过充电、正极材料等，这些因素也将直接影响锂离子电池寿命。

此外单体电池之间容量不一致[7]也会影响电池系统的总使用容量，具体表现为容量较小、性能较差的电池将提前达到满充电状态，但容量大、性能好的电池不能达到满充电状态。若不及时处理电池容量的不一致，电池组中的单体电池容易形成短板[8]，“短板”单体会先充满电也会先放空电，所以短板的存在会严重影响电池组的循环寿命，而短板单体是无法修复的，目前大多采用更换电芯的方式进行处理。为了缓解甚至消除电池组中各单体电池间的不一致性，提高电池组的性能、寿命和安全性，通过均衡电路和均衡控制策略[8]能够有效地改善这一缺点。

目前国内外检测LiFePO4电池一致性以及短板效应的方法比较少，杨思文等[9]提出了一种LiFePO4电池一致性筛选的方法，通过电池充放电能量效率和电压差值筛选异常电池，然后根据电池容量对剩余的分档电池进行初次分档，再以SOC(state of charge)状态下直流内阻值进行细化档位。孙振宇[10]的电池故障诊断方法研究主要应用于纯电动汽车动力电池，采样点远不如储能电站中产生GB(Gigabyte)级的数据量。肖健夫等[11]提出利用充电电压曲线距离分析和局部LOF(local outlier factor)检测方法诊断不一致单体，该方法十分依赖于阈值设定且没有说明电压平台期的影响。Li等[12]提出了一种LiFePO4电池一致性管理系统的策略，根据放电过程中阻抗变化的趋势信息，分析电池的电化学特性来区分LiFePO4电池的一致性。

系统中电池一致性好坏是一个相对概念。在实际使用时通常直接给定一个经验值，用于界定好坏，但是这一方法依赖于主观经验，而且可能由于工况原因或者参数设置不合理，导致判定结果变得完全相反，这不符合事实和大规模运用实际。

综合来说，上述方法都很难同时兼顾分析准确度和即时性的要求，因此本文提出图1所示流程方案，利用电池充放电特征数据，基于高斯分布与Grubbs 检验相结合的统计学方法，并通过特征分类后再进入经验库进行过滤，最后通过可优化系数对问题紧急程度进行排序。该方法的优点在于结合多种高效又简洁的数据异常值检测算法交叉验证，而且可以直接甄别哪些电芯属于短板问题，哪些电芯属于可均衡一致性问题，直接给出问题处理的优先级排序结果，对专家阈值的依赖性较小。

图1 总体流程框架示意图Fig.1 Schematic diagram of the overall process framework

1 模型建立及方法原理

当前储能电站架构基本为三级架构：箱-堆-簇，其中电池簇概念参考国家标准GB/T 36276 中的定义[13]，储能电站允许单簇成箱(或堆)，结构方案跟储能电站容量配置、场地大小等密切相关。故本工作选取电池簇作为分析对象。以下分别以两种常用场景(削峰填谷、调频)的储能电池簇充放特征开始分析，并因此确定可适用于工程实际的、简便又较为高效的综合模型，对结果分类处理后按优先级排序。

1.1 储能电站中电池簇的充放特征

“削峰填谷”模式中，储能的每日充放电时段较为固定，每日充放循环次数较少，且对储能充放电倍率要求较低，此场景应用注重电池使用容量。

电池簇的使用容量与所有单体运行一致性密切相关。电池簇可用容量Capacityused，可视为是单体的实际容量Capacitysingle-battery之和与一致性因子α的乘积，其中α≤1，α越大，表示一致性越好。

系统中直接采集的数据主要有单体电池电压、簇电压、簇电流、温度等，簇电流无法反映差异性；温度受温控系统影响较大，涉及系统结构，且非极端温度对电芯的影响是复杂的，属于一种长期积累的影响，需要庞大的数据量进行分析；电压数据是本工作中主要使用的数据，由于电芯自身存在差异性，达到一定程度时即会使得电芯电压数据出现不一致现象。图2、图3为某调峰电站日运行的典型工况曲线，反映全部指标数据在一天内的变化情况，其中图2可视化指标有簇电压、电流、SOC、温度，图3呈现部分(1～10号)单体电压情况。

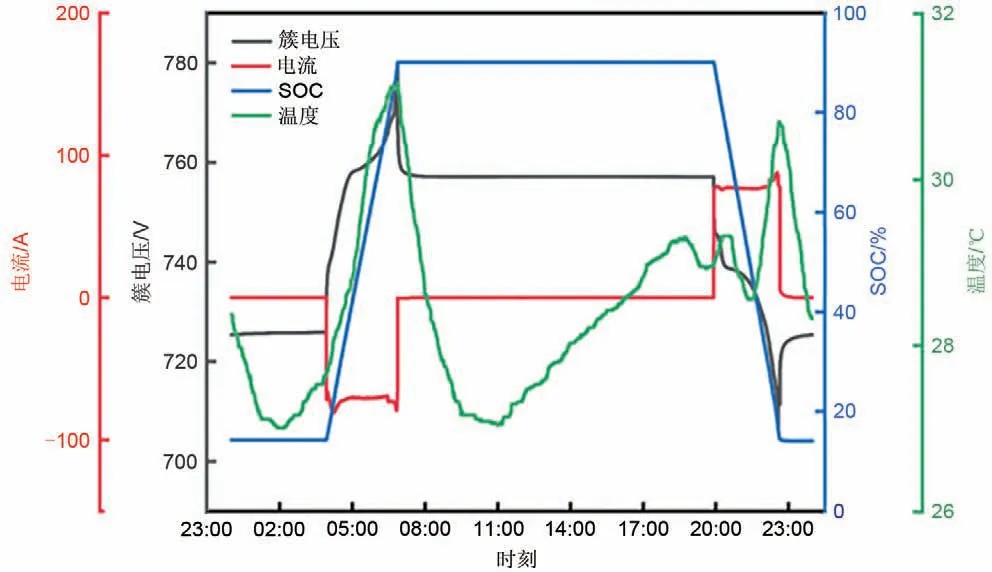
图2 某簇日运行工况曲线(调峰电站)Fig.2 Daily operating condition curve of a battery cluster(the peak load regulation of power)

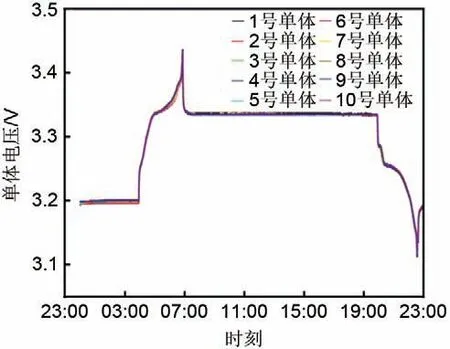
图3 某簇1～10号单体电压运行工况曲线Fig.3 Daily operating condition curve of a battery cluster(1～10 cells)

图4、图5、图6为所有单体电池电压均值、温度特征分别加入到图2、图3 中得到的特征图。从图4中可知，当日工况为一充一放，为一次削峰填谷应用，SOC 范围为10%～90%；从图5 中可知，平均温度曲线变化幅度不大，最大温差不超过10 ℃；从图6中可知，采集的簇电压基本与单体平均电压变化趋势一致。

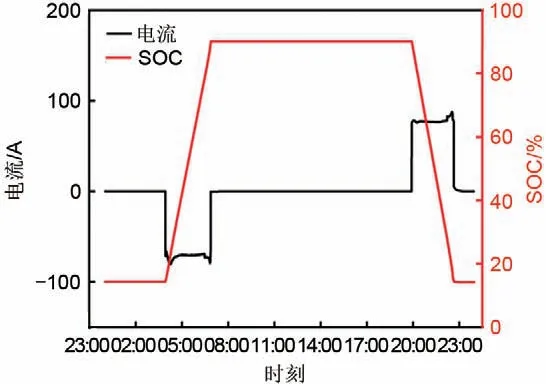
图4 运行工况的电流、SOC特征Fig.4 Current and SOC characteristics of operating conditions

图5 运行工况的温度特征及范围Fig.5 Temperature characteristics and range of operating conditions

图6 运行工况的簇电压、单体电压特征及范围Fig.6 Cluster voltage and cell voltage characteristics and range of operating conditions

电流虽大部分时间稳定在一定范围内，但由于其为瞬间变化量，容易受到扰动，故通常不建议直接进行分析；电芯电压为渐变状态变化量，图3中电芯电压曲线为连续光滑曲线，容易找到数值间的差异，从而确定一致性情况。

由于LiFePO4单体电池充放电过程中均存在一定的电压平台期，当电池处于平台期时，电压的离散程度较小。处于平台期的单体电压数据无法保证分辨精度，故本文直接采用电池放电末端的数据进行离群点的分析，此时电池电压变化斜率较大，只要电池一致性不佳时，便会产生较为明显的离群现象。

电池储能的另一应用场景：辅助调频。这一类应用场景具有频繁充放电切换的使用特征。图7以某调频电站典型日运行曲线为例。每一次的充放电特征都与调峰场景下的特征相似，但并非每一次的充放电数据均可作为有效分析数据源，仅能对某些充放电工况末端具有较大差异处的数据进行分析。由于电池短板或SOC 不齐等问题一旦存在，那么在短时间内不会发生突变，因此系统区分这些问题时，可只针对极值电压(称作全局极值)所在时段数据进行分析，从而降低数据量和分析难度，保证工程化使用的便利性。

图7 某调频型储能电站某一簇运行工况曲线Fig.7 Daily operating condition curve of a battery cluster(frequency modulation of power)

针对全局极值处的单体电压特征分布进行研究，发现单体电压离均值电压的差值(称作电压压差，单位V)符合多峰高斯分布模型，如图8 所示。理论上，电压值虽然为渐变的状态变化量，但是实际上还是会受到多种因素的综合影响，如温度不一致、生产工艺差异等。假定各种主因素之间相互独立，互不影响，并且具有相同的方差(δ2)，则有单体的压差x，服从k峰高斯分布的概率密度函数(p)为

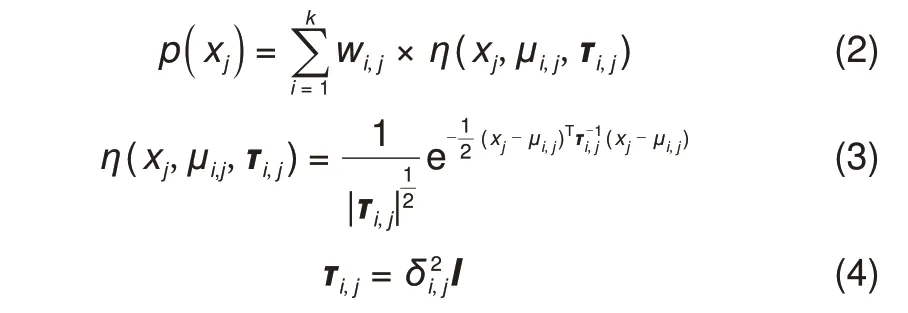
图8 某簇全局极限处压差频率密度分布图Fig.8 Distribution of differential pressure at the global extreme value of a battery cluster

式中，k为单高斯分布总数，代表存在k个主要影响因素，参考取值1～3；wi,j为第j类的第i个高斯分布的权重；j= 1,2，代表2种类型：充电末端或放电末端；η(xj,μi,j,τi,j)为第j类的第i个高斯分布；I为单位矩阵；τi,j为表示方差的矩阵；μi,j为其正态分布。

特别地，由于问题电池影响，当存在堆积型异常数据时，会产生一个小的尖峰，即使得实际情况的k值也会比理论的k值大1(当存在M个模组不齐时，最多可能有s.t:k→k+M个峰)；正常分布情况下，多个峰均值基本满足μ= 0；当忽略温度等因素时，则可以看成单峰正态分布，并且归一化处理后满足标准正态分布，即z-score:x～N(0，1)。

事实上，不管储能用于调峰还是调频或其他方面，都离不开电池的充放电行为，也必然存在全局极值电压统计量。若分析最高、最低电压对应时刻的全部数据也无法分辨出离群点，则表明电压一致性的系数因子较高，不影响平时整体应用，可暂不处理。

1.2 综合模型及问题分类

1.2.1 数据异常值检测

基于工程实践难度和准确度的综合考虑，本工作提出一种基于特征组合高斯分布模型与Grubbs检验法的综合应用。

基于第2 节针对LiFePO4电池的储能电站充放电特征的讨论，电池在充放电末端的压差符合k峰高斯分布规律，电芯问题(非突然性内短路)大都属于渐变型，发生的概率为小概率事件，故本工作选用了可调参的高斯分布的拉依达准则作为其中一个判别条件。

标准正态分布N(0,1)的拉依达法则：数值分布在(-3,3)中的概率约为99.73%。当某个样本数据落在(-∞, - 3]∪[3, + ∞)的概率极小时，大概率证明此样本偏离正常值。关于一元正态分布N(μ,σ2)的概率密度函数可以描述如下

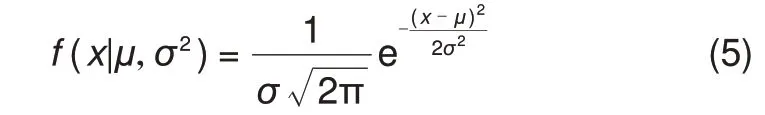
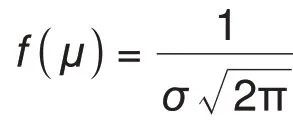
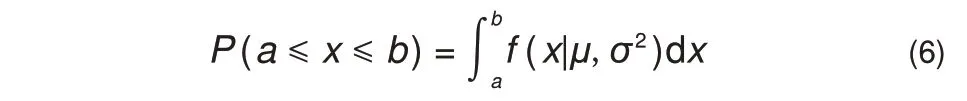
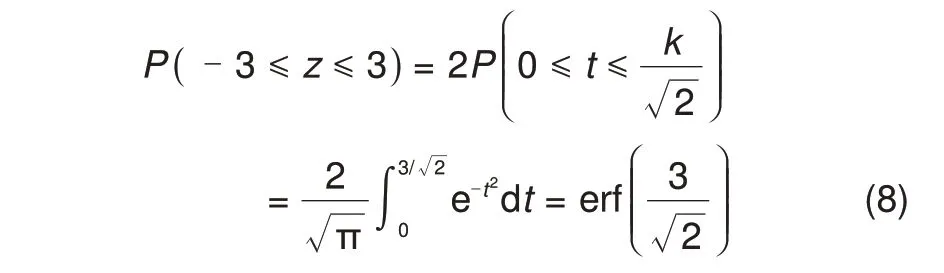
其中erf是高斯误差函数(Gauss error function)，定义为

由于在单簇中所有单体电压的压差实际情况并不严格满足单峰正态分布，通常由于1～3 个主因素综合作用，会产生多峰叠加的正态分布，但其主因素比较固定而且视为多正态分布的线性叠加，因此仍可以借鉴正态分布的拉以达准则用来判别异常值，只是实际σ作为加权多个单峰高斯分布的标准差，在3σ范围内，概率未必一定为99.73%，因此本工作仅借鉴该思想，使用可调参的3σ判别，可控地去检测真正的异常值。

另一方面，为了降低单一的高斯分布参数的影响，需要结合另外一种方法去交叉验证检测异常值。本文工作使用格鲁布斯(Grubbs)法，因为该方法的综合率(包含处理异常值时的误判率以及找不出异常值的错误率)是相对较小的一种方法。

使用Grubbs 检验法时，对每一个可能的异常值xout，计算Gn，公式如下

式中，σ为样本标准差；为样本均值。

当查询Grubbs 的临界值表Gp(n)，满足Gn＞Gp(n)，判定为异常值，使用单边检验方式，从压差大的优先检测或以矩阵形式并行检测。

关于单边检验方式的临界值的计算式如下

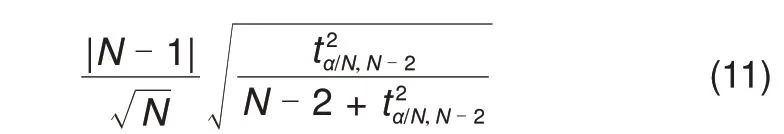
式中，N代表样本数量，这里实际代表一个电池簇内所有待检测电芯总数；tα/N,N-2表示t-分布[14]中自由度为N- 2、显著性水平为时的临界值。

1.2.2 问题分类方法

针对已交叉验证发现的异常数据，还需要进行进一步归类，以便甄别出其中分别属于电芯的哪种问题，目前本工作主要目的为工程化可在线区分出短板电芯、短板趋势、SOC 不齐电芯、不齐模组等问题。由于短板电芯具有“先充满电也会先放空电”的特性，因此可以使用正态分布甄别出异常点，结合原始压差数值直接进行异常电压偏高(低)状态判别。

结合两种算法以及问题特征，比如“短板”类型与“短板趋势”类型的区分规则：当充电与放电末端两类异常节点为同一个，并且满足充电末端为电压偏高状态，放电末端为电压偏低状态时，则可以预判为该节点为短板电芯，并且通过Grubbs 检验，区分属于强问题电芯还是弱问题电芯，弱问题电芯对应为短板趋势电芯，强问题电芯对应为短板电芯。详见图9 流程图，可实现综合判定并归类，其中异常结果中电压偏高电芯集合记为Up，电压偏低电芯集合记为Down，同一个模组位置的电芯记为OnePack。

图9 综合模型判定并分类Fig.9 Comprehensive model judgment and classification

各类问题数学语言描述的判别准则如下：

（1）设定集合DB ={j|j∈Up,j∈Down}，作为预分的短板类型，j为对应的单体序号；

（2）设定Grubbs 检验区分后的强问题电芯集合S1 ={j|j∈f1}，f1为使用高显著性水平的检验结果集合；弱问题电芯集合S2 ={j|j∈f2}，f2 为使用低显著性水平的检验结果集合；

（3） 实际短板电芯集合duanban=(DB∩S2)∪S1；

（4）设 定 备 用 集 合A= {j|j∈Down，j∈S2，j∉duanban};

（5） 设 定 备 用 集 合B= {j|j∈Up，j∈S2，j∉duanban};

（6）短板趋势电芯集合C = A ∩B；

（7）实际上不齐电芯集合SUp={j|j∈A，j∉C}，下不齐电芯集合类似；

(8) 模 组 上 齐 集 合， PUp= {j|j∈SUp，j∈SUp，j∈OnePack}，实际使用策略如图9流程所示。

1.3 分类后的优先级排序

基于上述综合模型方法得出的分类结果，可进一步进行主观方法再度筛选，控制输出结果量。最后需要对该结果进行优先级排序，有2 种方法：一种是直接使用压差大小进行排序；另一种是计算偏差容量作为优化系数，然后依据系数可排大小。其中第一种方法的优点是计算简单，除了充放末端数据外，没有多余的任何数据量，对于单个簇内的问题优先级，可以直接通过压差表征，但是对于不止一个电池簇的电站系统而言，不同簇间计算出来的压差不能直接进行排序，因为参考系不一样，压差大小本身与SOC 有关；第2 种方法的原理是：直接利用充放末端所在的充电或放电过程数据计算出问题电芯相比其余电芯的偏差容量，再直接通过偏差容量系数进行排序，偏差越大说明可运维优化度越高，应优先考虑进行处理。第2种方法需要计算容量，因此需要对应时段的电流数据，计算精度依赖于电流采集精度，且辨识相对的偏差时段可能会由于工况特殊性难以进行(图10)。

图10 某充电末端处优化系数计算示意图Fig.10 Schematic diagram of optimization coefficient calculation at the end of charging

2 模型的应用与验证

为了验证提出模型的可行性，本工作以某调峰电站典型日运行曲线数据为例，实际运行数据进行在线电池问题检测。在工程化条件下，使用高斯分布检验流程如图11 所示，其中σ、V_s1、V_s2、V_s3、V_s4为可调参数；使用Grubbs检验流程如图12 所示，检验显著性水平α=0.005对应强问题，α=0.05对应弱问题。具体使用参数如表1所示，用图1所示的流程框架按BMU内电芯节点编号统计，如图12所示，其中详细输出结果如表2所示。

图11 工程化使用高斯分布检验流程图Fig.11 Engineering use Gaussian distribution inspection flow chart

图12 工程化使用Grubbs检验流程图Fig.12 Engineering use Grubbs inspection flow chart

表1 工程化应用测试时具体参数配置Table 1 Specific parameter configuration during engineering application testing

表2 检测箱中当前共计问题4 处，分布于3 个电池簇当中。其中优化系数为-1，表示该簇中存在更严重问题的电芯，未计算偏差容量。图14 为其中3 箱1 堆1 簇问题情况第5 号单体为短板电芯，第48号单体为电压下不齐电芯。

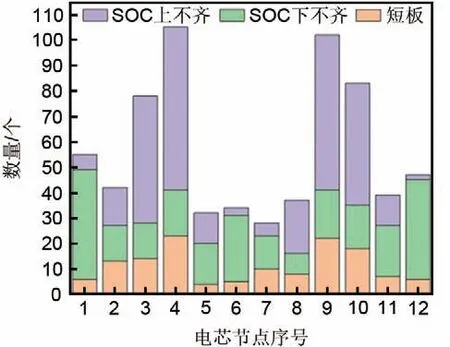
图13 某站累计检测问题按节点分Fig.13 The accumulated detection problems of a station by node points

图14 3号箱1堆1簇运行特征曲线Fig.14 Operating characteristic curve of 3-1-1

表2 3号箱问题检测结果Table 2 Problem detection results of three box

在实际应用中，可按照上述流程进行准确度检验，工程应用结果表明，当前模型及方法准确度μ≥99%，α≥85%。综上所述，本工作提出的方法具有较强的实用性，可用于电站在线检测。

图15 算法准确度检验流程Fig.15 Algorithm accuracy verification process

3 结 论

本文提出了一种可工程化的在线检测储能电站电池问题的方法，通过组合模型提高对离群电压值的辨别，可以较为快速又准确地识别问题电芯位置，此外还结合充放电电池的特征，实现对问题的分类，通过系数呈现最终处理结果的优先级排序，便于有效指导工程上电站运维工作。但是，随着人们对电池系统安全性的越发重视，必然不再满足只及时有效处理存在的问题，更需要对潜在问题的准确预测，本文方法虽可进一步通过微调辨识参数和输出的控制来预测系统中潜在的电芯问题，但是对时间性关联不强，还需进一步研究与探索。