压缩空气储能系统释能环节轴系建模与振荡分析

刘 迪，张甜甜，彭宇维，唐晓梅，王 丹，毛承雄

（华中科技大学电气与电子工程学院，湖北 武汉 430074）

电力储能技术可以提高电力系统的调度运行灵活性，促进电力系统对新能源的稳定安全消纳，实现高品质供电[1-2]。在众多电力储能技术中，压缩空气储能(compressed air energy storage，CAES)具有储能容量大、循环寿命长、响应速度快和功率调节灵活的特点，可以满足电网侧大规模储能的应用需求，并且绝热式CAES系统不受地理环境和生态等因素的制约，因此CAES技术在电网未来长远的发展中具有广阔的应用前景[3-4]。

目前国际上已有的两座商业化运行的CAES储能电站均采用补燃式CAES 技术，分别为德国Huntorf 储能电站和美国McIntosh 储能电站。我国近年来正积极发展新一代带储热的绝热式CAES技术，已经相继建成了500 kW、1.5 MW 和10 MW的CAES示范系统，下一步系统容量将朝着百兆瓦级继续发展[5]。相对于传统的补燃式CAES 技术，先进绝热式CAES技术(AA-CAES)摆脱了对化石燃料的依赖，具有更高的循环能效。在传统火电燃料日渐枯竭的今天，CAES技术可对未来以风力、光伏新能源发电为主体的新型电力系统提供重要支持，协助消纳新能源波动，减少“弃风，弃光”，助力节能减排与“碳达峰，碳中和”目标实现，提高电网的安全性、经济性和可靠性。

CAES系统作为一套完整的热力-机械-电气系统，由燃气轮机系统发展而来，CAES系统同样具有压气环节和透平环节，但不直接参与电能生产，通过将环境空气压缩至储气罐或大型盐穴内部，实现大容量高效储能，无燃烧室的CAES系统不存在爆炸或有害气体排放，直接利用清洁能源的富余电能，具备削峰填谷能力，更具备集约化、清洁化的优势[6]。当前CAES 的研究主要集中热力学、机械传动与电气特性等方面。文献[7-9]建立了CAES系统的热力特性模型，从系统设计角度研究了系统效率与压缩机膨胀机总压比和级数、等熵效率、压比分配以及换热器效能之间的关系，为CAES系统整体效率的优化和提升提供了参考。文献[10]和[11]建立了完善的部件变工况模型，揭示了不同工况下系统各参数的耦合关系及变化规律，从运行工况角度为CAES的优化运行提供了参考。文献[12-14]均采用永磁电机和变流器组合的并网发电形式，通过最大功率追踪算法来控制电机转速，从而实现CAES系统释能环节发电功率或效率的最大化。文献[15]和[16]分别探讨了CAES 在电力系统的协调调度和调相方面的优势和综合效益。上述文献分别从CAES的热力、机械、电气这三个重要组成部分着手进行数学建模与分析，但对于上述子系统之间的能量转换与耦合关系，尤其是CAES系统释能环节，作为机械能向电能转换的关键技术，针对其机电耦合机理和运行稳定性的研究较少，相比于传统同步发电机、风机等轴系串联结构，CAES的轴系振荡机理更为复杂，轴系质量块数目更多，且多采用串并联结合的方式[17-18]，目前，鲜有文献从轴系模型角度探讨系统中潜在的振荡形式。例如电力系统中的短路故障、甩负荷、非同期并网和自动重合闸等冲击性大扰动都可能激发系统的轴系扭振。另外，随着现代电力系统的发展，风电、光伏等新能源经过串补线路并网，串补输电系统可能与储能系统轴系交互影响，出现次同步振荡现象，导致较严重的系统稳定性问题[19]，其对轴系安全的影响同样不可忽视。

因此，本工作对压缩空气储能系统释能环节进行轴系模型建模，从机械电气耦合模型角度，分析其潜在振荡形式，为进一步采取提升CAES接入系统稳定性措施提供依据。首先，介绍了一种典型的四级膨胀的CAES发电系统机械电气耦合模型，建立了其数学模型；其次，根据所建轴系的数学模型，以10 MW 级CAES 系统为例，分析该系统的固有轴系振荡模态；最后，搭建仿真系统并通过设置扰动分析储能接入系统潜在的振荡形式，其结果与固有轴系振荡模态分析吻合，并提出了针对不同振荡形式的抑制策略。

1 轴系模型建模

1.1 结构形式

目前，CAES系统容量正不断提高，不仅意味着膨胀机需要具备更高的功率容量和膨胀比，而且在设计上单台膨胀机难以同时兼顾高容量、高压比和高效率，因此多级膨胀和级间再热将是未来大容量压缩空气储能系统发展的主流结构形式[20]。图1展示了一种典型的四级膨胀的CAES发电系统机械电气耦合模型，机械部分由4台膨胀机、多耦合齿轮箱和同步发电机构成，同步发电机经由变压器接入电网。

图1 CAES系统机械电气耦合模型Fig.1 Electromechanical coupling model of CAES

多耦合齿轮箱是整个机械系统的核心部件，将多台额定转速不同的透平膨胀机的机械功率进行转换和集成后传递至同步发电机，并在输出额定转速上与同步发电机匹配。由于各膨胀机的原动转矩和发电机的电磁制动转矩分别作用在多耦合齿轮箱的不同轴段上，机械功率实际上是通过各轴段两端发生相对扭转实现传递的[21]。当整个机电系统处于稳定运行状态时，不同轴段传递的扭矩也是稳定的，其两端相对扭转角保持不变。而当系统转矩出现不平衡时，各轴段两端相对扭转角会随之进行调整直至稳定。

因此，在对CAES系统机电耦合机理和潜在的振荡形式进行研究时，不能简单地将整个机械系统等效为一个刚性集中质量块，而应当考虑各轴段的扭转，建立起对应的轴系模型。本工作采用经典的分段集中质量弹簧模型[22]，该模型将各个膨胀机叶轮和发电机转子分别等效为刚性集中质量块，其只有转动惯量；各质量块通过弹性轴段与齿轮箱中的齿轮连接，各弹性轴段只有刚度没有转动惯量，其转动惯量分配到两端的质量块上，反映了各机械部件之间的耦合关系。在建模过程中，首先分析单质量块的数学模型，再推导至多质量块数学模型。

2.2 建模中对各部件的处理

该CAES 系统释能环节轴系结构如图2 所示，这是一个典型的多分支轴系结构，模型中除了常规的刚性集中质量块和弹性轴段外，还包括了多耦合齿轮箱中连接各分支的多个齿轮，建模时需要分别对其进行考虑。传统汽轮发电机组的轴系属于串联分布结构：所有旋转部件串联在同一旋转轴上同步旋转。而该CAES系统释能环节轴系为并联分布结构，各旋转部件分布在多耦合齿轮箱的不同轴段上，各轴段通过齿轮啮合进行耦合连接且额定转速不同，从而增加了轴系建模的难度。

图2 CAES轴系齿轮结构示意图Fig.2 Shaft gearbox structure of CAES

对于单质量块的轴系建模，其结构与汽轮发电机组轴系建模相似，如图3所示。

图3 单质量块轴系齿轮结构示意图Fig.3 Schematic diagram of single-mass shafting gear structure

以第j个质量块为例，其运动方程可描述如下

式中，ωj和ωNj分别为第二个质量块的角速度和额定角速度；Tj为该质量块的输入转矩；δi、δj和δk分别三个质量块的相对转角。对此求解可获得单个质量块的轴(系)振荡模态。

对于多质量块轴系建模，一般来说，多耦合齿轮箱中各齿轮的啮合刚度很大，各齿轮间可视为刚性连接，各齿轮的运动状态具有一致性[23]。因此其转角、转速和传动转矩可按照齿轮间的传动比进行转换，其关系如式(2)所示。

式中，θm和θn分别为齿轮m和n的转角；ωm和ωn分别为齿轮m和n的旋转角速度；Tm和Tn分别为齿轮m 和n 传递的转矩，r为齿轮m 和n 之间的传动比。

同时齿轮箱各小齿轮的转动惯量可以集中等效到主轴大齿轮上，作为一个刚性集中质量块，其等效关系如式(3)所示。

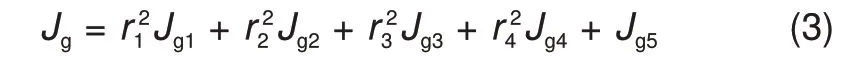
式中，Jg1、Jg2、Jg3、Jg4和Jg5分别为各齿轮自身转动惯量；r1、r2、r3和r4分别为各小齿轮与主轴大齿轮之间的传动比；Jg为齿轮箱等效刚性集中质量块的转动惯量。

因此整个集中质量块模型中一共包含了6个刚性集中质量块和5个弹性轴段，其轴系分段集中质量弹簧模型结构如图4所示。

图4 CAES轴系分段集中质量弹簧模型Fig.4 Lumped spring-mass model of a CAES shaft

图中，Ji为各质量块的转动惯量；J5为齿轮箱等效质量块的转动惯量；Ki为各轴段的刚度系数；ωNi为各轴段额定转速；Tmi为各膨胀机输出的机械转矩；Tem为同步发电机电磁转矩。

通常为了使整个膨胀过程的效率达到最优，各台膨胀机的设计额定工作转速都不相同，且最高额定工作转速可达上万转，因此该轴系模型具有较强的复杂性、高速性和多耦合性。

2.3 数学模型

根据牛顿第二定律和胡克定律，结合式和可得到系统轴系运动方程如式(4)、(5)和(6)所示

式中，θi为各质量块相对于其额定转速旋转参考轴的机械转角；ωi和ωNi分别为各质量块机械角速度和额定角速度；Di为各质量块阻尼系数；Tsum为输入齿轮箱的总机械转矩。

为了便于后期对系统轴系模型进行标准化建模和潜在振荡形式分析，需要对各参数进行标幺化处理，建立系统轴系标幺模型。在系统基准容量SB 确定的情况下，系统轴系标幺模型运动方程如式(7)、(8)和(9)所示

其中，各参数标幺转换关系如式(10)所示

3 固有振荡模态分析与计算

3.1 系统实例

以某10 MW 级CAES 系统为例，采用上述方法对其释能环节轴系模型进行建模。系统中四级膨胀机额定转速均不相同，从第一级到第四级额定转速依次为20000、14000、8000 和5000 r/min。同步发电机频率为50 Hz，其额定转速为1500 r/min。系统基准容量SB 选取为发电机额定容量10 MW，各质量块转动惯量参数如表1所示，各轴段刚度系数如表2所示。

表1 各质量块转动惯量参数Table1 Typical inertia parameters

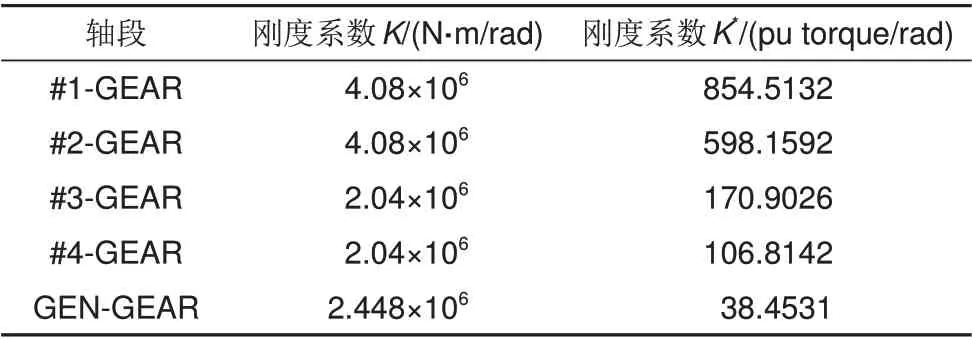
表2 各轴段刚度系数Table 2 Typical spring constants

通过对比表1 和表2 中标幺前后的各参数可以发现，标幺转换后的各质量块和各轴段参数大小排列关系与标幺前差异巨大，由标幺转换公式可知其大小排列规律与各膨胀机额定转速存在很强的相关性，因此各膨胀机额定转速的设计对整个系统轴系标幺模型参数影响巨大。

3.2 固有振荡模态计算与分析

采用特征根分析法对系统轴系标幺模型进行求解，得到整个轴系的固有振荡模态，其固有振荡频率和各振荡模态分别如表3 和表4 所示。各振荡模态中各质量块对应的数值表示其机械转角θi或机械角速度ωi振荡的幅值，正负代表振荡的相位。

表3 轴系固有振荡频率Table 3 Inherent oscillation frequencies of the CAES shaft

表4 轴系各振荡模态Table 4 Oscillation modes

从表3 和表4 可以看出系统一共具有5 个固有振荡模态，若把轴系刚体振荡模态也计算在内，轴系一共有6 个振荡模态，刚好是总的质量块个数。轴系固有振荡频率的频段分布广泛，其存在于低频段、次同步频段和高频段。从轴系各振荡模态中各质量块振荡相位来看，其翻转数n正好等于该模态固有振荡频率对应阶数n。

由于整个轴系模型为多分支多耦合结构，各振荡模态中各质量块间机械转角θi或机械角速度ωi的幅值和相位并不能直观反映各轴段扭转情况。通过对各振荡模态进行处理转换，得到各轴段在各振荡模态的轴上传递相对扭矩如图5所示，其中为了便于比较分析，以各振荡模态下的最高扭矩作为单位1对各轴段扭矩进行归一化处理。

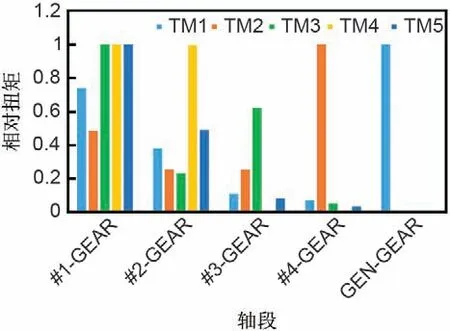
图5 CAES轴系各振荡模态下各轴段相对扭矩Fig.5 Torsional modes of oscillation of CAES shaft

从各轴段的扭转情况来看，#1-GEAR 轴段参与振荡模态最多，且轴段扭转情况最严重，其次是#2-GEAR 轴段；其余轴段则主要在特定振荡模态下发生严重扭转，而对其它振荡模态参与度较小，以GEN-GEAR 轴段为例，其只在5.37 Hz 对应的振荡模态下发生严重扭转，而对基本不参与其它振荡模态。总体而言，额定转速越高的轴段，对振荡模态的参与越多，轴段受到的扭转威胁也越大。

轴系发生严重的扭振可能会对整个机械系统造成严重破坏，危及CAES系统的安全运行，因此需要在系统运行过程中对轴系扭转情况进行监测。由于#1-GEAR 轴段发生的扭转程度最高，因此在该轴段上布置扭振监测传感器效果最好。

3.3 轴系稳定性分析

整个CAES轴系模型同时包含了发电机的电气量和各台膨胀机的机械量，因此需要分别从发电机侧和膨胀机侧对轴系稳定性进行分析，从而对系统潜在的振荡模态和振荡形式进行分析和评估。以各同步发电机电磁转矩Tem和膨胀机自身机械转矩Tmi为输入，各轴段扭矩Tti为输出，各质量块阻尼系数设为0.8，结合系统轴系运动方程，对各输入输出之间进行幅频响应分析。标幺模型中各轴段扭矩Tti如式(11)所示：

以同步发电机电磁转矩Tem为输入，各轴段扭矩Tti为输出，各固有振荡频率下系统幅频响应如表5 所示。从表中增益数据可以看出从发电机侧，即电气侧，容易被激发的是第一阶、第三阶和第五阶轴系振荡模态，其中第一阶振荡模态对应的各轴段输出扭矩增益最高，最容易被激发，对轴系安全运行威胁最大。当然各轴段输出扭矩增益均小于零的振荡模态并不代表该振荡模态一定不会发生，当模态电气阻尼为负时振荡同样可能被激发。

表5 各轴段扭矩Tti对发电机电磁转矩Tem的响应Table 5 Torsional amplitude-frequency response under different electromagnetic torque conditions

各轴段扭矩Tti对各台膨胀机自身机械转矩Tmi的响应情况较为类似，其增益均大于0，因此轴段上各阶振荡模态均可以由每一台膨胀机的机械转矩输入激发，在此不做赘述。以各轴段扭矩增益最高的振荡模态为主导模态，增益次高为次主导模态，同步发电机和各台膨胀机转矩输入的模态响应差异如表6所示。

表6 各轴段扭矩对各转矩输入的模态响应Table 6 Torsional mode under different input torque conditions

总体而言整个CAES 轴系模型的稳定性较差，存在多个容易引起共振的固有振荡频率点。其中同步发电机侧的轴系稳定性要好于膨胀机侧，但由于固有振荡频率同时存在于低频段、次同步频段和高频段，且200 Hz 为电网频率的倍频，因此CAES与电网交互中可能存在着多种振荡形式。

4 潜在振荡形式与仿真验证

当整个CAES 系统处于发电释能的稳定状态时，各台膨胀机输出稳定的机械转矩，多耦合齿轮箱各轴段均保持在额定转速，同步发电机向电网输出稳定的电磁功率。当系统发生扰动时，整个轴系的转矩平衡状态会被破坏而发生扭振。扰动可以分为两个方面：机械扰动和电气扰动，在实际运行中二者可能同时存在。机械扰动主要来自膨胀机侧，包括气源波动、调速阀门抖动、高压空气参数突变、换热故障、膨胀机叶轮振动等；电气扰动来自电网侧，包括短路、甩负荷、负荷突变、自动重合闸等[24]。不同特征类型的扰动对系统稳定性的影响不同，同时产生的振荡情况与系统自身参数密切相关，通常包括以下三种振荡形式。

4.1 冲击性振荡

此种类型的振荡通常由冲击性的大扰动激发，如短路故障、甩负荷、非同期并网和自动重合闸等，其造成的轴系扭振幅值与扰动的大小正相关。由于电力系统中各类保护措施的存在，此类故障性扰动通常持续时间很短，当扰动消失后振荡便开始衰减。该种振荡对轴系寿命的损害具有瞬时冲击性和长期累积性，因此在系统设计时应保证各轴段具有足够的抗冲击强度和扭转疲劳寿命。

以三相短路故障为例，对此类振荡特性进行分析。在CAES系统额定发电工况下，变压器高压侧母线发生三相短路故障，故障持续时间为0.06 s，2个工频周期，各轴段扭矩仿真波形如图6所示。

图6 齿轮箱各轴段扭矩仿真波形Fig.6 Torsional oscillation waveforms

从仿真波形可以看出，各轴段上的扭矩均出现了冲击性振荡，其中扭矩峰值最高的是GENGEAR轴段，扭矩峰值相对于其额定扭矩最高的是#1-GEAR 轴段。通过对扭矩进行频谱分析发现，振荡的主要频率成分为5.37 Hz，其他频率成分占比很小，同时各轴段扭矩振荡幅值大小与图5 中5.37 Hz对应振荡模态中各扭矩相对大小关系一致，因此冲击性扰动所激发的振荡形式为第一阶固有振荡模态。

此种类型的振荡是系统在经受冲击性扰动后恢复到正常运行状态的一种过渡过程。冲击性扰动的发生和大小本身并不可控，但可以采用一定的阻尼手段来加快振荡衰减平息，如附加励磁系统阻尼控制器，从而降低振荡对轴系寿命的累积性伤害。

4.2 次同步振荡

此种类型振荡是一种机械系统与电气系统相互作用从而产生自激的一种机电耦合振荡，其发生机理与汽轮发电机组次同步振荡机理类似。从实例系统的固有特性来看，其存在着数个次同步频段的固有频率点，当电气系统参数合适时，即电气侧自然振荡频率与轴系某个固有振荡频率互补，有可能会发生轴系与电网的耦合谐振，即次同步振荡[25]。

以接入风电场的CAES系统为例，对此类振荡进行验证和分析。正常状态下CAES系统与风电场协同运行，对风电场不稳定的输出功率进行平滑，整个系统通过串联电容补偿对外进行大规模输电，其结构如图7所示。

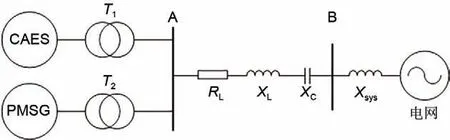
图7 含CAES的风电场并网外送模型图Fig.7 Wind farm system with CAES

其中PMSG 表示多台直驱风机组成的风电场，总装机容量为100 MW；XC为串联补偿电容容抗，串补度为41%。风电场初始有功出力为50 MW，CAES处于额定发电工况，有功出力为10 MW。稳态运行下，10 s时在母线B处施加一个持续时间为0.01 s 的三相短路故障，各轴段扭矩波形分别如图8所示，串补电容两端A相电压波形如图9所示。

图8 齿轮箱各轴段扭矩仿真波形Fig.8 Torsional oscillation waveforms

图9 串联补偿电容A相电压Fig.9 Voltage of Xc

从扭矩波形图可以看出各轴段扭矩均出现了次同步频率的振荡，且振荡幅值在不断增长，另外串补电容两端电压也出现了幅值不断增长的振荡。经频谱分析，各轴段扭振的主要频率成分为26.43 Hz，串补电容电压的主要频率成分为23.57 Hz，显然这两个频率是互补的，因此CAES的机械系统与电网之间发生了次同步振荡，其振荡形式为轴系第三阶固有振荡模态。

次同步振荡对CAES整个轴系的危害极大，在机械系统和电气系统不断相互激发下，振荡能量会不断进行累积。如果在次同步振荡发生后不能得到有效的抑制或切除，CAES系统各部件将承受数倍于额定值的扭转、剪切和挤压应力，严重威胁整个机械系统的安全运行。同时电网侧串补电容两端不断升高的电压会对其绝缘造成威胁，影响其使用寿命，严重时还会造成串补电容击穿。根据次同步振荡的特点，可以从以下几个方面对CAES系统次同步振荡进行抑制：①在机械侧或电气侧安装扭振传感器对次同步振荡进行监测，以便及时采取措施；②使用附加励磁阻尼控制器，为同步发电机励磁系统提供抑制次同步振荡的阻尼控制信号，提高系统对次同步振荡的阻尼；③采用可控串补(TCSC)技术，在次同步振荡发生时适当调整补偿度，避开机电耦合谐振点，从而使得振荡平息。

4.3 超同步振荡

整个CAES 轴系是一个复杂的高速耦合系统，其中存在着多种超同步频段扰动，如膨胀机叶轮振动、旋转轴由于不对中或不平衡引起的扰动和电网谐波等。当扰动的频率与轴系固有振荡频率相等或相近时，轴系就有可能发生共振，激发出对应的振荡模态。由固有振荡特性分析可知，示例系统轴系存在一个200 Hz 的固有振荡频率，恰好为电网频率的倍频，存在被电网谐波激发的潜在可能。电网谐波电流流经定子绕组时，会产生作用在轴系上的电磁转矩，由定子转子频率转换关系可知5次谐波(250 Hz)在轴系产生的电磁转矩波动为200 Hz，因此选取5次谐波来验证此种类型振荡。

当CAES系统处于额定发电工况时，在变压器高压侧母线并入5次谐波发生器，向同步发电机注入5次谐波，电流大小为20 A，各轴段扭矩波形分别如图10所示。

图10 齿轮箱各轴段扭矩仿真波形Fig.10 Torsional oscillation waveforms

从波形图可以看出整个CAES轴系在电网5 次谐波的作用下发生了超同步振荡，各轴段扭矩振荡频率为200 Hz，且振荡幅值大小与图5 中200 Hz对应振荡模态的相对扭矩大小关系一致，因此超同步振荡的振荡形式为第五阶固有振荡模态。

此类型振荡本质上是超同步频段扰动引发的一种轴系共振，不仅会缩短轴系寿命，对轴系安全运行造成威胁，而且会增加同步发电机的损耗和发热，降低电能质量。根据其发生机理可以从以下几个方面来对其进行抑制：①优化改进系统动力学设计，对系统中各潜在的超同步频段扰动进行校核，避免与轴系固有振荡频率重合发生共振；②提高各部件加工和装配精度，降低高速运行中的不平衡，从而减小超同步频段的机械扰动；③在发电机机端装设有源或无源滤波器，对电网侧超同步频段电气扰动进行抑制和消除。

5 结 论

本工作建立了CAES释能环节轴系分段集中质量弹簧模型，并针对某一系统实例进行了轴系固有特性和稳定性分析，在此基础上对系统中潜在的振荡形式进行了分析和仿真验证，仿真结果准确可靠，并得到以下结论。

（1）CAES 释能环节采用多耦合齿轮箱结构，有别于传统同步发电机的轴系串联方式，CAES采用轴系并联结构，其轴系振荡在不同类型扰动下均具有新的特点。

（2）CAES释能环节轴系具有复杂性、高速性和多耦合性，其固有振荡频率分布广泛，不同振荡模态下各轴段扭矩振荡幅值差异巨大，同时在电气侧和膨胀机侧有着不同的轴系稳定性。

（3）CAES释能环节轴系存在多种潜在振荡形式，对应着不同频段的多种振荡模态，根据其振荡特性可分为冲击性振荡、次同步振荡和超同步振荡，从而为后续振荡抑制策略研究奠定了基础。