风冷电池模组热性能及成组效率的多目标优化

（上海工程技术大学机械与汽车工程学院，上海 060；上海机动车检测认证技术研究中心有限公司，上海 0805；青海交通职业技术学院，青海 西宁 8000）

我国新能源汽车产业发展规划(2021—2035年)提出，到2025 年新能源汽车新车销售量达到汽车新车销售总量的20%左右，电动汽车的发展获得新动能。锂离子电池作为目前电动汽车的主要动力能源，具有能量密度高、放电电压高、自放电率小、循环寿命长、无记忆效应等诸多优点。然而锂离子电池的安全性和效率都与其温度密切相关，电池包内部的热量不能及时散出会导致电池温度急剧上升、电池温差变大，甚至引起热失控[1]。所以，电池热管理系统(BTMS)对电动汽车尤为重要。

电池热管理方法主要有风冷、液冷和相变材料(PCM)冷却方式及其复合冷却。风冷配置结构简单，系统运行稳定可靠，成本低，容易实现[2]。相比风冷，其他冷却方式具有更好的热性能[3-5]，但成组效率低，成本与维护费用高。在目前的文献中，对风冷电池热管理的研究大部分都是对电池模组的冷却空气流道进行设计与优化[6-8]。另外，增加换热结构来加强电池模组内部与冷却空气的换热能力，也是一种简便易行的电池风冷热管理方案[9-10]。Na 等[11]通过在圆柱形锂离子电池模组内部设置横向隔板使模组能够进行逆向风冷，但该结构需要设置两个隔离风道，进排风需要专门设计。

需要指出，在对电池模组的优化研究中，大部分工作只考虑电池模组的热性能表现，而对电池模组的其他设计指标并没有进行综合考虑，而电池温度的望小设计与电池模组成组效率的望大设计之间互相矛盾，需要进行平衡设计。Wang 等[12]对电池模组的风冷结构进行了多目标优化，得到相邻电池的最佳间距，提高了风冷电池模组的热性能，但是没有结合电池模组的成组效率进行优化。电池模组的重量成组效率即电池与电池模组的重量之比反映了电动汽车电池包的能量密度，是电池热管理设计的核心任务之一[13]。

为了提高风冷电池模组的热性能并兼顾较优的成组效率，本文提出一种基于双层套筒式热扩散板结构的新型风冷电池热管理系统及其优化方法。首先研究进口风速v0以及热扩散板厚度H、套筒长度Hs和热扩散板尾部长度L等结构参数对电池模组热性能的影响。然后，以最高温度Tmax、最大温差ΔT、进出口压差Δp以及成组效率Gm作为优化目标，利用中心复合设计(CCD)实验方法建立相应的代理模型，并结合期望函数对热扩散板配置下的电池模组进行多目标优化。

1 数值仿真模型

1.1 电池模组的建立

图1(a)为风冷电池模组的示意图，电池模组多个LG18650 锂离子电池正交排列，电池底部通过电绝缘板与底部铝板连接，且电池间配置套筒式热扩散板，进而增强电池模组的换热性能。为了减少计算量，根据对称性取出电池模组代表性区域进行计算，如图1(a)中红色方框区域所示。图1(b)为双层热扩散板配置的仿真模型，由于过大过小的电池间距会影响电池模组的成组效率和热性能，所以本文中1/2×5 颗圆柱电池等间距4 mm 布置[14]，电池底部垫有电绝缘板，厚度为1 mm，最底部为铝制底板，厚度为4 mm。

图1 电池模组结构示意图Fig.1 Diagram of battery module

1.2 数值计算模型

本文对仿真计算模型进行如下假设：①假设单体电池内部均质各向异性，并且单体电池内部产热均匀；②忽略电池-热扩散板之间的接触热阻；③电池模组内部冷却空气为不可压缩牛顿流体；④所有材料的热物性参数都是恒定的常数；⑤忽略热辐射的影响；⑥通过模拟仿真，发现电池模组在有极耳连接和无极耳连接下的最高温度偏差在0.27 ℃，故在本文主要模拟计算中忽略电池间的极耳连接。对于仿真中的控制方程以及k-ε湍流方程均基于参考文献[15-16]。

空气的连续性方程

空气的动量守恒方程

空气的能量守恒方程

电池的能量方程

式中，u,v,w分别是沿x,y,z方向的速度分量；ρa,ρb,ca,cb,ka,kbx,kby,kbz,Ta,Tb分别表示冷却空气和电池的密度、比热容、导热系数以及温度；Qb为电池的发热量；t表示时间；μ为空气动力黏度；μt为湍流动力黏度系数；p为压强。根据实验室已有的研究，LG18650 电池的发热量与放电倍率C之间呈二次关系[17]

冷却空气横掠电池时，空气的雷诺数Re需要根据模组中空气的最大速度Umax进行计算，即Re=ρaUmaxDcell/μ，这里最大速度Umax=v0Scell/(Scell-Dcell)[18]。其中Dcell为电池的直径，v0为进风口的风速，Scell为电池之间中心间距。当空气进口速度由0.5 m/s 增加至5 m/s时，计算所得的雷诺数范围大约从2767到27669，所以对电池模组仿真时，选用k-ε湍流模型进行计算。本文考虑电池导热的各向异性，径向导热系数和轴向导热系数分别为1.63 W/(m·K)和36.96 W/(m·K)[19]，表1 中列出了各个材料的热物性参数。

表1 不同材料热物性参数Table 1 Thermo-physical properties of different materials

1.3 边界条件设置与网格无关性验证

本文采用商用计算流体力学软件Fluent 17.0进行双精度瞬态模拟仿真，且LG18650 圆柱电池放电倍率均为3 C，根据公式(3)设置单体电池的产热量为1.86 W。环境温度与进风口温度均设置为25 ℃，计算区域的网格划分如图2所示。然后设置能量方程残差收敛条件为小于10-6，其余控制方程残差收敛条件为小于10-4。边界条件中入口采用速度入口边界条件，出口适当延长以降低回流，并采用压力出口边界条件，壁面采用无滑移边界条件。

电池模组上下两端均设置为绝热界面，左右两侧设置为对称界面。网格是在Ansys Meshing中创建，考虑了固体与流体介质之间的耦合传热，其中包括电池与空气流动区域之间的接触面，均进行渐变网格膨胀层的设置，如图2 红框中所示。另外，网格无关试验表明，当计算网格单元数从256081增加到506520 时，电池模组最高温度以及进出口压差的偏差分别小于0.08%以及0.14%，前者网格设置可以满足计算要求，为了节省计算时间，选用前者网格设置。

图2 网格以及边界条件Fig.2 Mesh system and boundary conditions

2 结果与分析

首先通过数值仿真研究各个设计参数对电池模组热性能的影响，包括进口风速v0、热扩散板的厚度H、套筒长度Hs以及热扩散板尾部长度L，然后通过中心复合实验设计(CCD)建立优化目标代理模型，并结合期望函数进行了多目标优化。本文中的数值仿真案例如表2所示，且所有案例中电池的放电倍率均设置为3 C。

表2 数值仿真案例Table 2 Numerical Simulation Cases

2.1 仿真结果验证

为了验证仿真模型的准确性，搭建了模拟电池模组的风冷系统进行实验验证。图3为电池模组的风冷实验系统，包括4×5的电池模组，模组装配有热扩散板，外壳为亚克力板，并包裹气凝胶毡进行绝热，所加工的热扩散板结构参数为H=1.5 mm，Hs=20.5 mm，L=25 mm。实验中，首先利用风扇调速器与热线式风速仪校定风速，使风速稳定于1 m/s，然后对环境温度与进口温度进行监测，待温度稳定在(25±0.5)℃时，采用直流电源(GWINSTEK PSW 160-21.6)为电池模组提供20×1.86 W的热源输入，对应3 C 放电产热功率。同时在电池模组内部的P1 和P2 监测点使用K 型热电偶和日置LR8410R温度采集仪进行电池温度监测。直流电源电信号输出精度在0.1%以内，风机采用离心式交流鼓风机，最大风压为240 Pa，最大风量为2.0 m3/min。实验采用同一厂家的K型热电偶，热电偶之间的偏差为0.1 ℃，在10 ℃温升测量精度估计为0.2 ℃或者2%。日置LR8410R温度采集仪精度在0.01 ℃，在0～100 ℃范围内温度准确度为0.6 ℃。另外，实验所用的热线式风速仪(希玛AR866A)能够检测0～30 m/s的风速，测量精度在0.01 m/s。在模组入风口和出风口还设有压力监测点，测量所用的风压变送传感器(速讯QDF70B-SX)在600 Pa 范围内测量准确度为1.5 Pa。

图3 实验系统和热扩散板结构Fig.3 Experimental system and the structure of heat spreader plate

图4中给出了实验结果与仿真结果的对比。对比结果表明，电池温度均随着放电时间的增加而增加，P1和P2点处实验与仿真最大温度偏差分别为2.66%(0.82 ℃)和2.34%(0.79 ℃)，可见仿真结果与实验结果吻合。在温升过程中仿真的结果略大于实验结果，在放电末端实验与仿真的偏差逐渐减小。这是因为在实验测试中，即使用气凝胶包裹电池模组外壳，仍然存在小部分热量的损失，而在仿真中电池模组的外部设置为绝热，所以导致实验结果略小于仿真结果。

图4 实验结果与仿真结果对比Fig.4 Comparison of experiment results and simulation results

2.2 仿真初步结果对比

为了验证热扩散板配置的有效性，本节对比研究了常规风冷与热扩散板配置下的基准电池模组的热性能，结果如图5所示。在没有配置热扩散板的常规风冷电池模组中，由于冷却空气的温度沿空气流道方向不断增加，即沿程加热效应，最高温度出现在风向下游最后一颗电池的内部，为39.45 ℃，最低温度出现在靠近进风口的第一颗电池的迎风面，电池模组的最大温差为5.61 ℃。

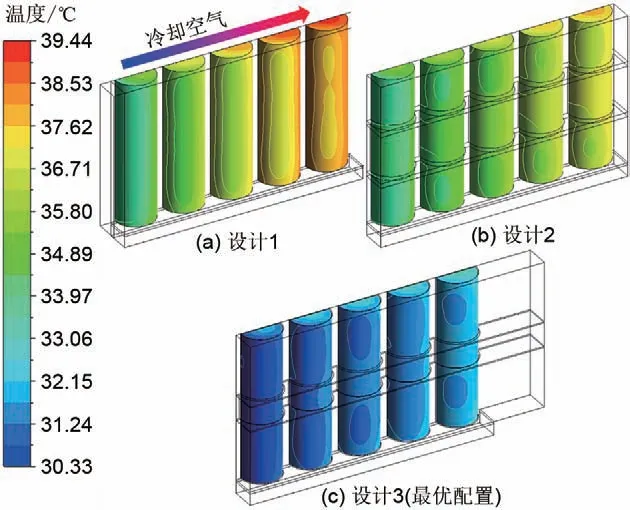
图5 电池模组温度分布云图Fig.5 Temperature distribution of battery module

电池模组中添加热扩散板结构(基准案例)的仿真结果如图5(b)所示。热扩散板结构配置下电池模组的最高温度与最大温差分别为37.98 ℃与4.28 ℃，相比常规风冷案例，电池模组的最高温度与最大温差分别降低3.71% (1.47 ℃)与23.68% (1.33 ℃)。可以看出，热扩散板配置下，电池模组的热性能有明显提高。

2.3 不同进口风速的影响

热扩散板配置下风冷电池模组在不同风速时的热性能以及对应的进出口压差如图6所示，电池温度随着流程增加而升高，最高温度发生在最下游电池。随着风速增加，最高温度逐渐减小，最后趋于平缓。而最大温差随着进口风速的增加，呈现出先快速减小后缓慢增大的趋势。当风速从0.5 m/s 增加至3 m/s 时，电池模组的最高温度与最大温差分别减小10.42 ℃与3.08 ℃，风速在3 m/s时温差达到最小为1.86 ℃。随着风速继续增加至5 m/s 时，电池模组的最高温度仅减小1.06 ℃，而最大温差稍微上升0.16 ℃。这是因为电池模组温差是由下游最高温度与上游最低温度之差所决定的，当进口风速在1～3 m/s 时上、下游电池降温显著，最大温差逐渐减小；而当风速大于3 m/s时，下游电池风冷换热性能趋于稳定，而上游电池受到冷却空气正面冷却持续降温，导致整体最大温差有所上升。

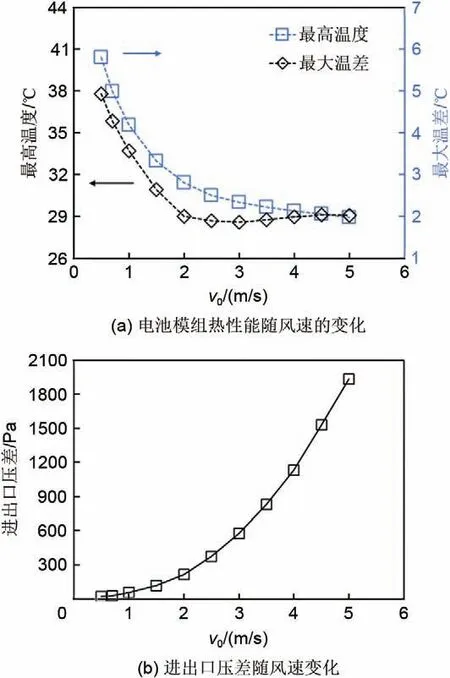
图6 不同进口风速的影响Fig.6 Effect of different inlet velocity

另外，随着风速的增加，进出口压差的上升趋势越来越明显，与风速平方正相关。当风速从0.5 m/s增加至3 m/s 时，进出口压差从14.56 Pa 增加至575.83 Pa，当风速继续增加到5 m/s 时，进出口压差为1935.27 Pa。综合考虑压差增大与温差控制，应适当降低进口风速范围，在保证电池模组热性能的前提下降低风扇设备功耗。

2.4 热扩散板结构参数的影响

本节研究热扩散板的结构参数对电池模组热性能的影响，图7(a)～(c)分别为热扩散板厚度H、热扩散板套筒长度Hs以及热扩散板尾部长度L对电池温度的影响。热扩散板厚度由0.5 mm 增加到5 mm 时，电池模组的最大温差随热扩散板厚度的增加而近似线性降低，减小20.06%，最高温度基本不变(降低0.81%)。这是因为热扩散板厚度的增加使热扩散板的均温性得到加强，上游电池温度有明显上升，减小了电池模组进出口处的电池温度差，进而使整体模组的最大温差得到降低。

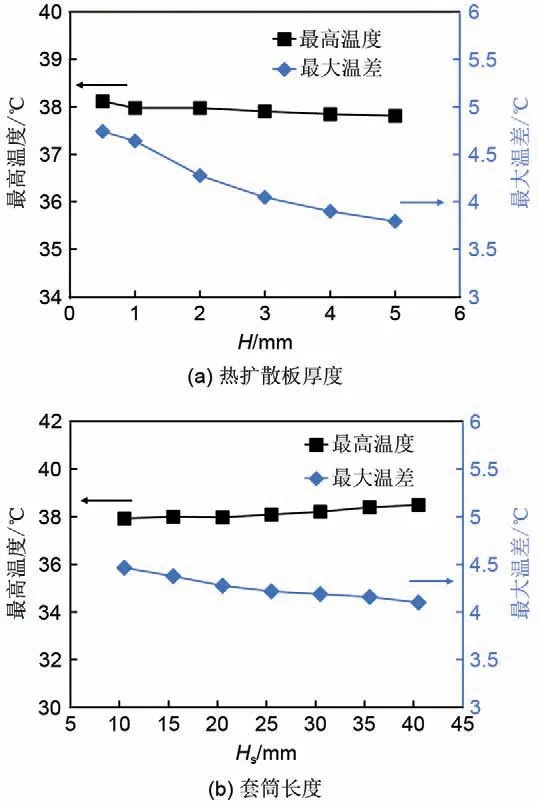
图7 扩散板结构参数对电池模组热性能的影响Fig.7 Effect of structural parameters of heat spreader plate on thermal performance of battery modules

当热扩散板套筒长度由10.5 mm增加至40.5 mm时[图7(b)]，电池模组的最高温度基本不变，但是最大温差降低8.09%。这是因为随着热扩散板套筒长度的增加，热扩散结构的均温导热性能增加而降低温差，与此同时，电池套筒长度增加，会增大套筒之间流阻、减弱当地空气流动和换热，使得电池上部最高温度位置的散热受到一定的抑制，进而导致最高温度基本不变或者轻微上升。当热扩散板尾部长度由2 mm 增加至25 mm 时[图7(c)]，相当于增强了最下游电池对流面积，电池模组的最高温度出现在倒数第二排电池，电池模组的最高温度和最大温差分别降低1.32%与10.21%。

2.5 多目标优化

在多目标优化过程中，不仅需要考虑电池模组的热性能，还要综合考虑其进出口压差Δp与成组效率Gm，其中成组效率为电池质量mb与包括电池模组底板和绝缘板的整体质量mtotal之比，即

成组效率Gm的值越大表明电池模组的能量密度就越高。

2.5.1 实验设计

实验设计包括热扩散板的3个结构参数与流速(H,Hs,L,v0)，每个参数有五个水平，则理论上一组全阵列实验设计需要54=625 个仿真案例，工作量大。本文基于中心复合设计(CCD)原则进行数值仿真方案设计，得出25 个仿真样本(见表3)，在不损失精度的前提下大大减少了样本数量[14]，并据此建立优化目标代理模型。对于两因子情况下的中心复合设计(CCD)星点设计，每个因子拥有五个水平(-α、-1、0、+1、+α)。若对于每个因子的取值范围为(a1,a2)，则

表3 CCD实验设计方案及其对应的数值仿真结果Table 3 The design cases generated by CCD method and corresponding numerical simulation results

式中，n为影响因子所对应的个数；0 水平为a1和a2的平均值，而-1 水平和+1 水平分别对应a1和a2的值。

2.5.2 代理模型及优化

基于上述25个研究案例及其仿真结果，利用实验设计分析软件Design Expert 11.0，通过响应面分析法进行多项式拟合。在方差分析中根据p值判断各个结构参数的显著性，将p值大于0.05的项剔除[20]，最后得出四个优化目标的二阶代理模型，每个模型的拟合优度R2、适应性拟合优度AdjustedR2以及预测拟合优度PredictedR2均大于98%。优化目标代理模型如式(6)所示

基于代理模型，引入期望函数D对热扩散板配置下的电池模组进行多目标优化，优化目标包括：最高温度(Tmax)、最大温差(ΔT)、进出口压差(Δp)以及电池模组的成组效率(Gm)。其中期望函数D由每个优化目标对应的期望值di组成，期望函数D的取值范围为0～1，如式(7)所示[14]

这里n为输入参数的个数即设计变量的总数，本文中设计变量包括：热扩散板厚度(H)、套筒长度(Hs)、热扩散板尾部长度(L)和进口风速(v0)；ri为第i个响应目标的重要性，本文中所有优化目标对应的ri值均为1，即优化目标具有相同的权重。由于Tmax，ΔT，Δp为望小设计，而Gm为望大设计，则各个优化目标对应的期望值di公式如下

结合四个优化目标的代理模型与期望函数进行公式(9)中所表示的多目标优化，在最高温度Tmax、最大温差ΔT、压差Δp的最小化与成组效率Gm的最大化之间取得平衡设计。

优化后的参数配置对应表2 的设计3， 其最高温度为33.09 ℃，最大温差2.89 ℃，进出口压差为81.79 Pa，成组效率为87.1%。为了进一步验证代理模型预测准确性，对最优配置下的电池模组进行了数值仿真，其温度分布如图5(c)所示。电池模组的最高温度为33.20 ℃，最大温差为2.87 ℃，进出口压差为82.20 Pa，成组效率为87.08%。最优配置下电池模组的代理模型预测结果与仿真结果偏差如表4所示。

与设计1 相比，多目标优化后的设计3 即最优配置，虽然成组效率下降2.63%、进出口压差增加66.69 Pa，但是最高温度与最大温差分别降低16.12%(6.36 ℃)和48.48%(2.72 ℃)，均明显大于成组效率的下降率。设计3 与设计2 相比，不但最高温度和最大温差分别降低12.88%(4.89 ℃)和32.48%(1.39 ℃)，而且重量成组效率也提升了3.51%。可见，最优配置(设计3)的成组效率不仅得到保证，而且温度一致性也得到有效提升。

3 结 论

（1）与常规风冷案例相比，基于本文提出的双层套筒式热扩散板配置的基准电池模组(设计2)最大温差降低23.68% (1.33 ℃)，最高温度也有一定程度下降。因此，引入热扩散板能够有效提高风冷电池模组的温度一致性与综合热性能。

（2）通过CCD 实验设计样本数据，建立了优化目标代理模型，并结合期望函数进行了多目标优化，包括最高温度Tmax、最大温差ΔT、进出口压差Δp的最小化以及电池模组成组效率Gm最大化。

（3）在进口风速v0为1.5 m/s 时热扩散板的最优配置结构参数为：热扩散板厚度H为0.5 mm，热扩散板套筒长度Hs为10.5 mm，热扩散板尾部长度L为24.7 mm。电池模组的最高温度约为33.09 ℃，最大温差约为2.89 ℃，进出口压差为81.79 Pa。相比常规设计，电池模组的最高温度和最大温差分别降低16.12%(6.36 ℃)和48.48%(2.72 ℃)，模组的温度一致性得到明显改善，另外重量成组效率也能达到87.1%，与常规设计的89.73%接近。

符号说明

ca,cb—— 空气与电池的比热容，J/(kg·K)

Dcell—— 电池直径，mm

Gm—— 电池模组的成组效率

H—— 热扩散板厚度，mm

Hs—— 套筒的长度，mm

ka—— 空气的导热系数，W/(m·K)

kbx,kby,kbz—— 电池在x、y、z方向上的有效导热系数，W/(m·K)

k—— 湍流动能，m2/s2

L—— 热扩散板尾部长度，mm

mb—— 电池质量，g

mtotal—— 电池模组整体质量，g

Δp—— 压差，Pa

Qb—— 电池产热率，W

Re—— 雷诺数

Scell—— 相邻电池的中心距，mm

Ta,Tb—— 相邻电池的中心距，℃

t—— 时间，s

Tmax—— 最高温度，℃

ΔT—— 最大温差，℃

Umax—— 相邻电池间的最大风速，m/s

u,v,w—— 沿x,y,z方向的速度分量，m/s

v0—— 进口速度，m/s

ε—— 湍流动能的耗散率，m2/s3

μ—— 空气动力黏度，Pa·s

p—— 压强，Pa

ρa,ρb—— 空气与电池的密度，kg/m3