苯加氢制环己烯装置能量系统集成及催化剂再生周期优化
赵丽文,刘桂莲
(西安交通大学化学工程与技术学院,陕西 西安 710049)
引 言
环己烯是重要的有机化工原料,广泛应用于医药、农药及其他精细化学品的生产。苯选择加氢制环己烯是大批量获得环己烯的常用方法。
反应系统是苯选择加氢制环己烯装置的核心,其关键在于高活性和高选择性催化剂的使用。工业上常选用钌(Ru)基催化剂以获得较高的加氢活性和环己烯选择性。生产过程中,受各种因素影响,催化剂活性随运行时间的延长而降低[1]。为确保反应速率、装置产能和产品质量,通常需要提高反应器温度。这些变化和调整导致反应器的进料、出料及相关流股的参数不断变化。
换热网络是该装置能量回收的核心。苯选择加氢制环己烯反应器的进料和产品分别是换热网络的热阱和热源,其参数变化影响换热网络的能耗。在整个生产周期内,反应单元和换热网络高度耦合,催化剂失活对能量系统的影响是复杂非线性的。当催化剂活性降低至一定值时,需要对催化剂进行再生以维持较高的经济效益;不同再生周期对应不同的单位环己烯生产成本。基于能量系统集成探究催化剂失活对苯加氢制环己烯装置参数的影响、优化催化剂再生周期对于稳定生产和降低生产成本具有重要意义。
以夹点技术和数学规划法为基础,国内外学者对能量系统集成优化进行了大量的研究[2]。吕东晖等[3]对某催化裂化装置进行全流程模拟,综合考虑能量系统集成和产品变化探讨了反应器操作温度对生产效益的影响。对于某煤制天然气变换单元,萧鸿华等[4]通过优化反应参数提高了系统效率,实现了反应参数和换热网络的集成优化。此后提出的基于夹点技术的图像法可集成反应器和换热网络、优化反应器的进/出口温度和能耗[5]。Tian 等[6]在加氢反应器和换热网络集成的基础上,基于模拟探究了汽柴油加氢装置催化剂活性对反应器进/出口温度、换热网络能耗及换热面积的影响。Zhang等[7]基于换热网络和反应器的集成研究了环氧乙烷生产工艺的循环优化,根据经济性能图优化回收率,实现了最大能量回收和最高年利润。上述研究主要针对某一稳态生产工艺的集成与优化,未考虑生产周期内催化剂活性变化引起的系统波动。Zhao等[8]的研究表明环己烯装置反应器和换热网络参数从催化剂使用初期至末期发生明显变化,影响单位产品能耗和单位产品成本,但未对该装置能量系统集成及催化剂再生周期优化进行系统研究。此外,催化剂再生周期优化对于节能降耗的重要意义尚未明确。
对于苯选择性加氢制环己烯技术,袁吴魏等[9]从反应机理、反应工艺及催化剂活性组分和制备方法等方面,综述了该技术的研究进展。苯和氢通过中间产物环己烯生成目标产品——环己烷,选用对环己烯有高选择性的催化剂才能有效地实现苯选择性加氢[10]。Ru 是苯选择加氢的高效催化活性中心,选择适宜的载体、助剂和添加剂是改善催化剂性能最有效的手段[11]。Yu等[12]证实利用亲水材料包覆钌可延缓苯和环己烯从水相向钌的扩散。Sun等[13]采用沉淀法合成的纳米Ru 基催化剂,可通过单金属Ru 和Ru-Zn 纳米颗粒与环己烯形成稳定的络合物以提高其选择性。Song 等[14]研制了一系列含锌、锂、铝的层状负载双氢氧化物的钌基催化剂(Ru/LDH),可以显著促进环己烯的生成。上述研究主要集中在改进催化剂性能。深入了解催化剂失活机理有助于找到降低其不利影响的动力学手段[15]。失活机理通常被分为三类:中毒、结焦、烧结或相变化[16]。刘颖等[17]对催化剂结焦失活的反应动力学方程进行了修正,提出了抑制催化剂结焦失活的方法。Yang 等[18]建立了预测催化剂失活总体趋势的集总动力学模型。Zhang 等[19]以铁催化剂为例建立了催化剂在整个生命周期内的结构-性能关系,用以揭示催化剂在全生命周期内的动态结构演化。Dey 等[20]概述了催化剂失活的预防、控制和处理方法,指出控制反应温度是降低失活速率的有效方法。文献调研表明,高效苯选择性加氢催化剂的制备及性能改进是当下研究的热点问题。然而,关于催化剂的研究主要集中在强化反应速率和提高目标产物选择性,尚未有研究探讨苯选择性加氢制环己烯装置的操作参数随催化剂失活的变化规律及催化剂再生周期优化。
本文拟基于反应动力学、能量平衡和源/阱变化对换热网络的影响规律探究系统参数随催化剂失活的变化规律,构建通用的反应-换热网络耦合模型。据此对苯选择性加氢制环己烯装置进行能量系统集成,以催化剂活性为自变量建立反应-换热网络耦合性能图,辨识不同催化剂活性对应的最佳反应器参数及公用工程消耗量,优化催化剂再生周期。
1 通用反应-换热网络耦合模型
1.1 反应器参数随催化剂失活的变化
对于包含n种组分的简单不可逆催化反应,反应方程可用式(1)描述[5]。

式中,Ai表示反应物或产物;ξi表示组分Ai的化学计量因子。对于反应物,ξi<0;对于产物,ξi>0;若Ai不参与反应,ξi=0。
催化反应器中,因为中毒、结焦、烧结和热失活等多种因素的共同作用,催化剂的活性随运行时间的延长逐渐降低,导致反应速率、反应参数及反应路径发生变化。在反应器设计中需考虑催化剂失活对反应速率的影响。分离动力学方程[16]将催化剂活性与反应速率项分开,可分别考虑催化剂活性和组分浓度的影响,如式(2)所示。对于全混流(CSTR)反应器,设计方程可表示为式(3)[5]。

式中,A1为关键组分;-rA1为A1的反应速率;k表示反应速率常数;cAi表示组分Ai的浓度;αi表示组分Ai对应的反应级数;FA1表示组分A1流量;X表示组分A1的转化率;V表示反应器体积;上角标0 表示反应器进口参数。
在催化剂、溶剂等影响因素固定的情况下,反应速率常数仅为反应温度的函数,并遵循Arrhenius方程,如式(4)所示[8]。

式中,A表示指前因子;E表示反应活化能;R表示通用气体常数,8.314 J·mol-1·K-1。
当反应发生在连续液相中,反应器出口中组分Ai的浓度cAi可由化学计量式表示,如式(5)所示。
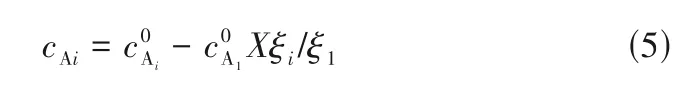
将式(3)~式(5)代入式(2)并整理,可得反应温度(T)、反应转化率(X)及催化剂活性(φ)三者间的关系,如式(6)所示。
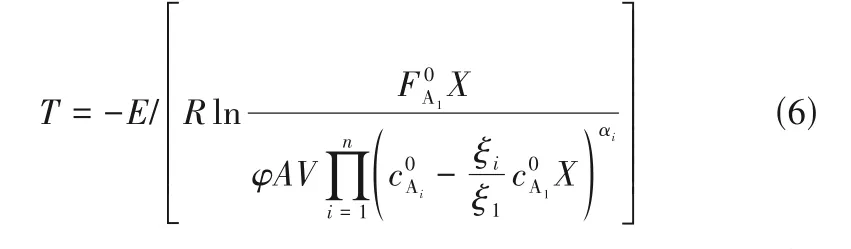
初始时刻,催化剂活性φ=1,可实现目标转化率Xmax。由式(6)可见,随着催化剂活性的降低,需提高反应器温度以维持该转化率。对于给定的催化剂,存在适宜使用温度范围[Tmin,Tmax]。当反应温度升高至使用上限Tmax时,为避免对催化剂产生不可逆损害,反应温度保持Tmax恒定,该情况下反应转化率随催化剂失活不断下降[8]。
根据反应器能量平衡,反应器温度(T)不仅受反应器参数的影响,还受反应器进口物料温度及反应器热负荷的影响。对于涉及n种组分的拟稳态CSTR 反应器,不考虑外界做功,其能量平衡如式(7)所示。
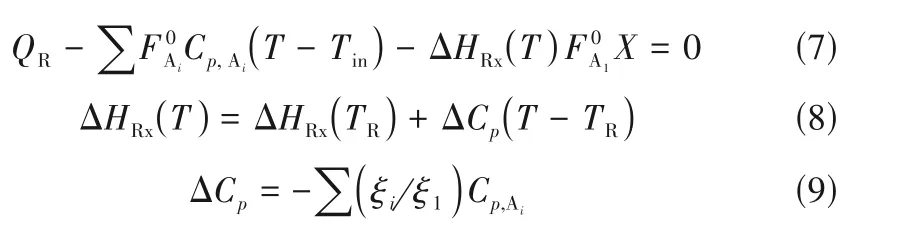
式中,QR表示反应器热负荷;Cp,Ai表示组分Ai的摩尔热容;Tin表示进料温度;ΔHRx(T)和ΔHRx(TR)分别表示反应温度T和参考温度TR下的反应热;ΔCp表示系统总热容变化。
式(7)中,QR也受反应温度变化影响。对于CSTR 反应器,反应器内温度处处相同,均为T。若反应器夹套内换热介质进出口温度分别为Ta1和Ta2,对于放热反应,T>Ta2>Ta1;吸热反应,Ta1>Ta2>T。反应器热负荷与反应温度之间的关系见式(10)。
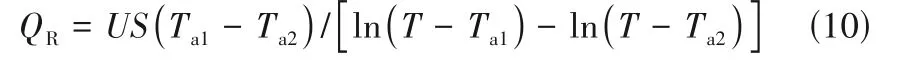
式中,U表示反应器总传热系数;S表示反应器换热面积。
把式(10)代入式(7)并整理可得式(11),以表征反应器入口温度、出口温度及转化率之间的关系。
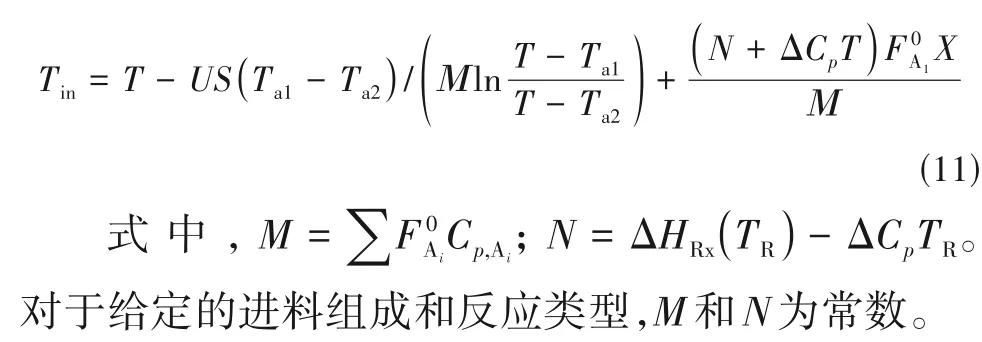
联立式(6)和式(11),可确定不同催化剂活性对应的反应器进料温度、出料温度、反应转化率及反应器热负荷。
1.2 系统目标能耗随催化剂失活的变化
生产过程中,反应器的进/出口物流通常需要被加热或冷却,为换热网络的热源或热阱。催化剂活性的变化影响反应器进口温度、出口温度以及相关物流的组成和流量,进而影响复合曲线、公用工程用量及夹点位置。
根据源阱的位置规则[5]可分析反应器进、出口温度及反应转化率变化对复合曲线及公用工程用量的影响。当催化剂活性变化时,进口物流温度、出口物流温度及反应器转化率不断变化,进而导致出口物流热容流率变化。若该过程中,反应器出口温度由T变化至T′,反应器入口温度由Tin变化至T′in,转化率由X变化至X′,对应出口物流热容流率变化量可由式(12)计算[8],反应器出口和入口流股焓值变化量可分别由式(13)和式(14)计算。当出口流股跨夹点时,出口流股焓值变化量分为夹点上和夹点下两部分[式(15)和式(16)],分别影响加热公用工程用量和冷却公用工程用量。

式中,CP表示流股热容流率;下角标in和out分别表示反应器进口和出口物流;ΔH1和ΔH2分别表示反应器出口和入口流股焓值变化量;ΔH3和ΔH4分别表示出口流股跨夹点时夹点上和夹点下的焓值变化量;上角标ini 表示参数初始值;上角标T 表示目标值;TP为夹点温度,若出口流股为热源,则TP对应热夹点温度,反之则为冷夹点温度。
假设夹点位置不变,不同情况下换热网络加热和冷却公用工程变化量汇总于表1[21]。当源/阱温度或热容流率变化导致冷热复合曲线靠近时,有可能形成新夹点。若夹点位置变化,需要将冷(热)复合曲线平移一定的距离(ΔHS)以满足最小传热温差的要求,换热网络的冷、热公用工程用量均需要在表中所示的基础上增加ΔHS。
根据表1 及式(13)~式(16)可确定不同催化剂活性对应的系统加热和冷却公用工程变化量。

表1 夹点位置不变时公用工程用量随反应参数的变化[21]Table 1 Variation of utilities along reactor parameters when the pinch position is unchanged[21]
1.3 催化剂再生周期优化
考虑到单位加热和冷却公用工程品质不同,在计算中将不同类型的能源按各自对应的能耗折成标准煤(kg ce)。在实际生产过程中,催化剂失活影响反应器参数及换热网络目标公用工程用量,反应转化率的变化进而影响目标产品产量,此过程中,单位产品的生产成本不断变化[8]。为了准确评价催化剂活性变化对系统的影响,需要综合考虑一个生产周期内的生产成本(包括操作费用和投资费用两部分)和目标产品产量。本文以单位产品平均生产成本(C)作为生产过程中的经济性评价指标。单位产品平均生产成本越低,经济效益越高。
对于稳定生产的化工过程,系统操作费用主要源自工艺用能,可由式(17)表示。
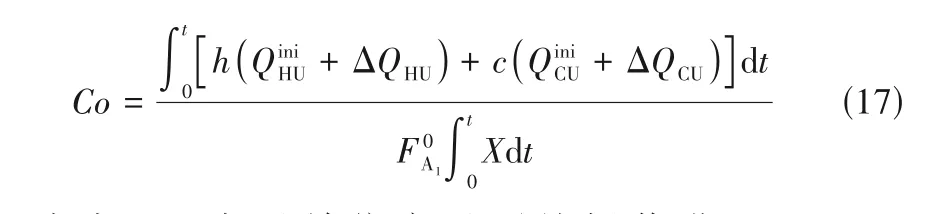
式中,Co表示单位产品平均操作费用,USD·kmol-1;h和c分别表示单位加热和冷却公用工程费用,USD·kJ-1;t表示催化剂由投产至再生所经过的时间,即再生周期,h。
对于不同类型的失活,催化剂活性均可表示为生产时间的函数[22],如式(18)所示,其反函数可表示为t=g(φ)=f-1(φ)。代入式(17)可得生产周期内单位产品平均操作费用与催化剂活性的关系,如式(19)所示。


式中,φreg表示催化剂再生活性。
投资费用主要考虑生产周期结束时再生或更换催化剂的费用。综合考虑催化剂再生费用、再生周期及目标产品产量,单位产品投资费用(Ci)可由式(20)确定。

式中,Ci表示单位产品平均投资费用,USD·kmol-1;c1表 示 单 位 质 量 催 化 剂 价 格 ,USD ·(kg cat)-1;Wnew表示需要购买的催化剂的质量,kg;c2为催化剂的再生费用,USD。对于特定的催化剂和生产工艺,c1可视为常数。通常,催化剂再生费用可以表示为催化剂活性的函数,随催化剂活性的降低而增大。但由于c2远小于c1,在再生费用和催化剂活性的关系缺乏相关理论支撑时,c2可简化视为常数。如果有相关催化剂活性与再生费用的关联关系,可在式(20)中用该关系替代催化剂再生费用c2。
结合式(19)和式(20),单位产品生产成本(C)与催化剂活性(φ)间的关系可由式(21)表示。
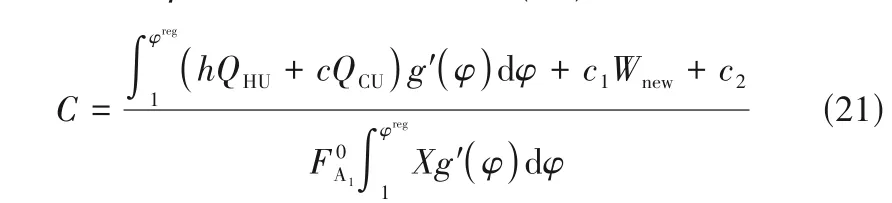
根据式(6)~式(21)可建立考虑催化剂失活的通用反应-换热网络耦合模型以及以催化剂活性为自变量的反应-换热网络耦合性能图,以展示系统的能耗、生产成本以及反应器参数在整个生产周期内随催化剂活性的变化。不同催化剂活性对应的反应器参数(X,T,Tin,QR)、换热网络能耗(QHU,QCU)均可由反应-换热网络耦合性能图直观高效地确定,指导反应器的设计和操作优化。
系统的最佳催化剂再生(更换)活性(φreg),对应最低单位产品平均生产成本Cmin,可根据反应-换热网络耦合性能图确定。当催化剂活性大于φreg时,再生催化剂将造成催化剂浪费,单位产品对应的投资费用过高;低于该活性时进行再生,则导致产品品质降低,能量利用效率降低,生产单位产品所需操作费用较高。根据φreg和式(18)可以确定催化剂的最佳再生周期(Treg)。
2 环己烯装置能量系统及催化剂再生周期优化
某公司通过液相苯加氢制环己烯,简化工艺流程见图1。粗苯进料经进出料换热器(E101)和进料加热器(E102)加热后进入苯预处理反应器(R101),脱除芳烃类杂质。脱除杂质后的液相苯和氢气在R102中发生加氢反应,生成目标产物环己烯。反应产物经闪蒸回收部分氢气后进入T201塔脱除水分,继而进入T202 和T203 塔中分离和回收苯。脱苯后的产物在塔T204 中分离得到环己烯产品。加氢反应发生在CSTR 反应器R102 中,主反应见式(22)。由于环己烷更加稳定,环己烯很容易进一步加氢生成环己烷,相应的副反应见式(23)。

图1 液相苯选择性加氢制环己烯工艺流程Fig.1 Flowsheet of liquid-phase benzene selective hydrogenation to cyclohexene

2.1 反应器参数随催化剂失活的变化
反应器采用Ru-Zn-B/ZrO2催化剂。该催化剂活性高、易吸附苯,生成环己烯的速度很快,环己烯从催化剂表面脱附或者生成环己烷较慢[23];高反应压力(>3 MPa)下,苯的转化率为50%~60%,环己烯的选择性为80%[9],此时可忽略副反应的影响,仅考虑主反应。以苯(BZ)为关键组分,考虑到生产过程中催化剂活性变化,高压下苯转化的速率方程可写为式(24),与氢压无关。反应速率常数可由式(25)确定。

一定温度范围内,升高温度有利于补偿催化剂失活,维持理想的苯转化率和环己烯选择性。文献研究[21]表明,催化剂活性φ=1时,系统的转化率Xmax=0.66,代入式(28)得反应温度与催化剂活性的对应关系,如式(29)所示。

该反应为放热反应,反应器夹套内冷却介质为水,假定冷却水的进、出口温度不变,分别为305 K和343 K,由式(10)得反应器热负荷与催化剂活性关系,见式(30)。

该反应苯处理量为982 mol·min-1,在298 K 和7 MPa反应条件下,主反应的标准反应热为-87090 kJ·kmol-1;根据式(11)可得式(31),以表征反应进口温度与催化剂活性的对应关系。
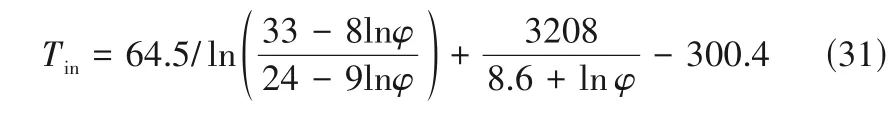
反应温度升高会导致苯加氢速率降低、环己烯收率下降。这主要是因为环己烯在水中的溶解度随温度升高而增加,产物易发生裂解,且催化剂发生团聚[24]。工业生产中,反应温度通常不超过473 K[25]。
由式(29)可得,当催化剂活性降低为0.75 时,反应温度约为470 K,为避免产物裂解,反应温度不再继续升高,即Tmax=470 K。代入式(28)可得该反应温度下转化率与催化剂活性的对应关系,如式(32)所示。
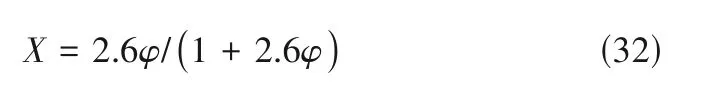
将式(32)代入能量衡算式可得T=470 K 时反应进口温度与催化剂活性的对应关系,如式(33)所示。
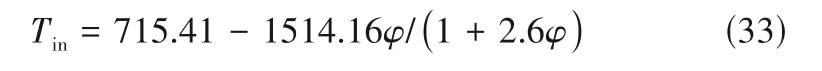
2.2 换热网络目标能耗随催化剂失活的变化
根据图1 分析可知,该过程的换热网络由8 股冷流和10股热流组成。冷却公用工程为冷却水,加热公用工程为蒸汽,反应器热量由冷却水移除。φ=1时的换热网络物流数据列于表2。
表2 中,热物流H1 为反应器R102 进口物流,热物流H3 为出口物流。取最小传热温差为10 K 时,该换热网络的冷热复合曲线见图2。由图可得,该过程的最小加热和冷却公用工程用量分别为6597.77 kW 和4850.26 kW(不包含反应器热负荷QR);平均夹点温度为380.2 K。

图2 温焓图(φ=1)Fig.2 The temperature-enthalpy diagram (φ=1)
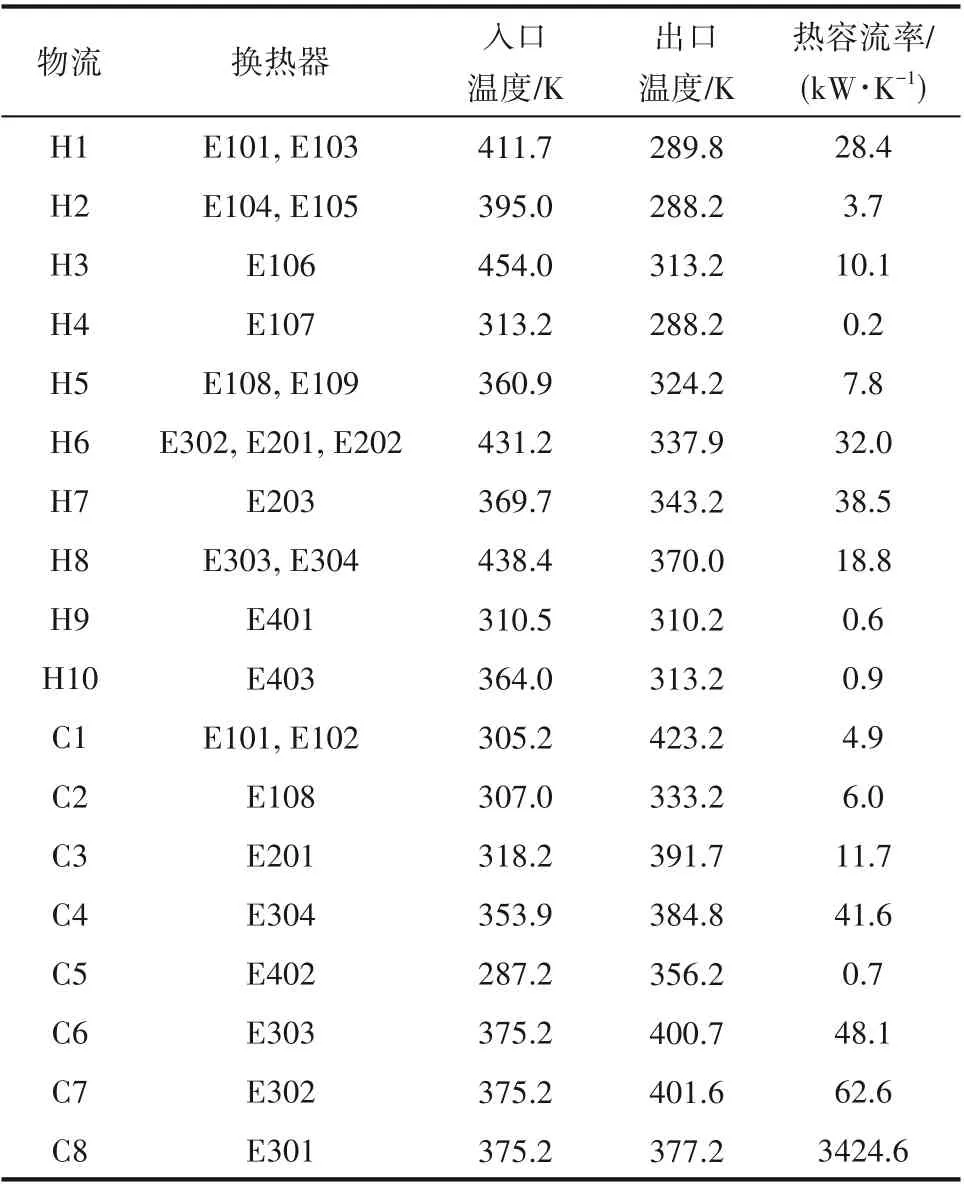
表2 φ=1时换热网络物流数据Table 2 Streams data of the HEN when φ=1
温焓图中,点A的横坐标对应H3 的始温,即反应器出口温度;点F的横坐标对应H1 的终温,即反应器进口温度;点B和点E的横坐标分别对应H3 的终温和H1的始温;PH和PC分别为热夹点和冷夹点。
假定系统参数波动时,夹点位置不变。由式(29)和式(32)可得,随着催化剂不断失活,H3 始温先增加、后保持不变,终温不变;热容流率先不变、后变化,热容流率变化量与催化剂活性的关系见式(34)。
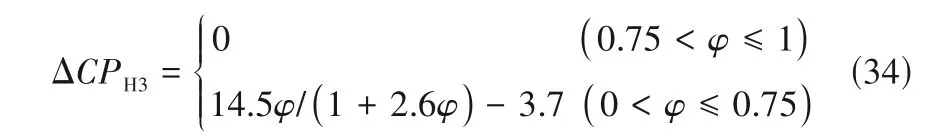
由式(31)和式(33)可得,H1 始温不变,终温随催化剂活性的降低不断增加。一个生产周期内,不同催化剂活性范围对应的出口流股的变化参数及进口流股在温焓图中位置不同,如表3 所示。根据表1,可求得不同催化剂活性范围内系统最小加热和冷却公用工程变化量,分别如式(35)和式(36)所示。

表3 进出口流股随催化剂失活变化情况Table 3 Variations of the inlet and outlet streams along catalyst activity

通过构建不同催化剂活性对应的系统温焓图验证了夹点不变假设的准确性,结果表明,随着反应器进出口流股温度和热容流率的变化,夹点温度不变,平均夹点温差始终为380.2 K。因此,不需要对冷热复合曲线进行平移,由式(35)和式(36)可以准确确定系统能量目标。
2.3 反应-换热网络耦合性能图及Ru-Zn-B/ZrO2催化剂再生周期优化
苯选择性加氢制环己烯过程中,催化剂失活的主要原因是苯中混有的杂质分解为毒性物质,使催化剂暂时中毒。催化剂呈指数型失活,失活级数约为1;催化剂活性与时间的关系可由式(37)表示[26]。催化剂失活可以视为反应器有效催化剂装填量的减少。反应器催化剂装填量为5745 kg,当催化剂活性降低为φ时,催化剂损失量为5745(1-φ) kg。工业催化剂再生后,催化剂活性比原有的活性有所下降,再生损失约占失活催化剂的10%[27]。因此催化剂再生后,需要补充部分催化剂,新增催化剂质量(Wnew)可据式(38)计算。
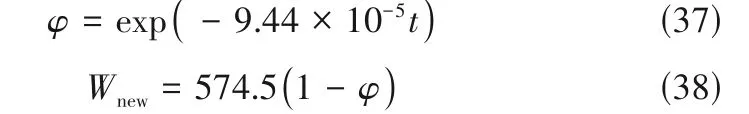
该反应冷热公用工程费用、催化剂购买及再生费用(h、c、c1和c2)分别为6.6×10-6USD·kJ-1、6.62×10-7USD·kJ-1、400 USD·(kg cat)-1和1.44×105USD。代入式(21)可计算不同催化剂活性对应的单位环己烯生产成本,并构建单位产品成本随催化剂活性变化曲线。根据式(29)~式(33)构建反应器进出口温度、转化率及反应器热负荷随催化剂活性变化曲线,根据式(35)、式(36)绘制公用工程随催化剂活性变化曲线,依据式(37)可绘制反应时间随催化剂活性的变化曲线,汇总可得反应-换热网络耦合性能图(图3)。
由图3可得,系统运行初始时刻,催化剂活性为1,对应转化率为0.66,反应器入口温度290 K,出口温度454 K,加热和冷却公用工程分别为6598 kW和4850 kW,与文献值[21]比较,误差小于0.2%。
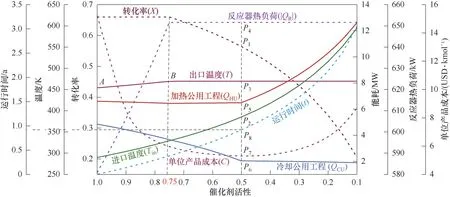
图3 苯加氢制环己烯流程反应-换热网络耦合性能图Fig.3 Reactor-HEN coupling diagram of benzene hydrogenation to cyclohexene process
由X-φ曲线可得,催化剂失活初期,反应器转化率恒定,当φ<0.75 时,反应转化率随催化剂失活不断下降。这是因为催化剂失活初期可以通过升温(T-φ曲线AB段)补偿催化剂失活,直至反应器温度升高至上限470 K(B点),此后反应温度维持恒定,转化率下降。
结合T-φ和Tin-φ曲线可得,反应器进出口温差随着催化剂的失活逐渐减小,催化剂失活至一定程度时,反应器出口温度低于进口温度。这是由于受催化剂失活影响,反应器转化率先恒定后降低(X-φ曲线),对应反应放热量[式(7)第三项]先恒定后降低,同时,反应温度先升高后恒定(T-φ曲线),对应反应器移热量先增加后恒定(QR-φ曲线);当反应器移热量大于反应放热量时,进出口温差为负值,即反应器出口温度低于进口温度。
由Q-φ曲线可得,催化剂失活前期,冷却公用工程用量迅速减少,加热公用工程用量变化缓慢;催化剂失活后期,加热公用工程用量迅速增加,冷却公用工程用量基本不变。原因在于,反应器进口物流H1 热容流率大于出口流股H3,H1 温度变化对公用工程影响较大。反应前期,H1 终温(反应器入口温度)较低,位于温焓图中夹点下方,其升高致使冷却公用工程用量减少。反应后期,H1终温位于夹点上,温度变化影响加热公用工程用量;与此同时,反应转化率急剧下降,夹点上方H3 物流热容流率降低,导致加热公用工程用量增加。
现行苯加氢制环己烯装置催化剂再生周期约2年,结合t-φ曲线和C-φ曲线可识别该活性对应的单位产品生产成本约为6.62 USD·kmol-1。C-φ曲线表明,催化剂使用至φ=0.5 时,对应单位产品生产成本最低,约5.29 USD·kmol-1。结合t-φ曲线可进一步确定该活性对应的再生周期Treg=0.92 年(P8点)。因此,若催化剂再生周期由2年优化至0.92年,单位产品生产成本可减少约19.9%。由X-φ、Tin-φ、T-φ、QR-φ、QHU-φ和QCU-φ曲线得,φ=0.5 时反应转化率为0.56(P1点),反应器最佳进口温度为385.4 K(P2点),出口温度为469.6 K(P3点),反应器热负荷为651.6 kW(P4点),加热公用工程和冷却公用工程分别为6492.3 kW和2035.3 kW(P5点和P6点)。
在系统投产运行阶段,根据图3 可准确识别不同催化剂活性对应的最佳反应器参数,结合自动监测和控制系统,可以实现对系统的实时、准确调控。
3 结 论
本文考虑催化剂失活构建了反应-换热网络耦合模型和催化剂再生周期优化方法,据此对苯选择性加氢制环己烯流程进行分析。构建的反应-换热网络耦合性能图可准确展示反应参数、换热网络能耗及单位产品成本随催化剂失活的变化规律。以平均单位产品生产成本为优化指标,该装置催化剂的最佳再生活性为0.5,对应的最优再生周期为0.92年。再生周期优化后,单位产品生产成本最高可降低19.9%。根据所提出的方法,无须复杂模拟计算即可确定Ru-Zn-B/ZrO2催化剂处于不同活性时对应的最佳反应转化率,最佳反应器进/出口温度,反应器热负荷以及系统的加热和冷却公用工程消耗量,结合自动监测和控制系统,可以实现对系统操作参数的实时调控,以保持产品产量,提高经济效益。
本文所建立的反应-换热网络耦合模型和催化剂再生周期优化方法仅考虑了主反应,仅适用于简单催化反应系统。对于复杂催化反应,反应器参数、换热网络参数与催化剂活性间的关系将更加复杂。本文推导的方程不能直接应用,但该分析方法可以进一步推广处理这类复杂问题。此外,催化剂活性再生周期的优化可能会增加系统开停车的次数,后续将进一步研究该因素对单位产品成本的影响,优化完善本文所构建的模型。
符 号 说 明
A——指前因子
Ai——反应物或产物
C——单位产品平均生产成本,USD·kmol-1
Cp,Ai——组分Ai的摩尔热容,kJ·kmol-1·K-1
ΔCp——系统总热容变化,kJ·kmol-1·K-1
Ci——单位产品平均投资费用,USD·kmol-1
Co——单位产品平均操作费用,USD·kmol-1
CP——流股热容流率,kW·K-1
c——单位冷却公用工程费用,USD·kJ-1
cAi——组分Ai的浓度,kmol·m-3
c1——单位质量催化剂价格,USD ·(kg cat)-1
c2——催化剂的再生费用,USD
E——反应活化能,kJ·mol-1
FAi——组分Ai的摩尔流量,kmol·h-1
ΔHRx——反应热,kJ·kmol-1
ΔH1——反应器出口流股焓值变化量,kW
ΔH2——反应器入口流股焓值变化量,kW
h——单位加热公用工程费用,USD·kJ-1
k——反应速率常数
QR——反应器热负荷,kW
R——通用气体常数,8.314 J·mol-1·K-1
rAi——组分Ai的反应速率
S——反应器换热面积,m2
T——反应器出口温度,K
Ta1——反应器夹套内换热介质进口温度,K
Ta2——反应器夹套内换热介质出口温度,K
Tin——进料温度,K
TP——夹点温度,K
t——催化剂由投产至再生所经过的时间,h
U——反应器总传热系数,W·m-2·K-1
V——反应器体积,m3
Wnew——新增催化剂质量,kg
X——关键组分A1转化率
αi——组分Ai对应的反应级数
ξi——组分Ai化学计量系数
τ——反应器空时,h
φ——催化剂活性
φreg——催化剂再生活性
上角标
ini——参数初始值
T——目标值
0——反应器进口参数
下角标
CU——冷却公用工程
HU——加热公用工程
in——反应器进口参数
max——最大值
min——最小值
out——反应器出口参数

