基于数据特征增强和残差收缩网络的变压器故障识别方法

马 鑫，尚毅梓，胡 昊，徐 杨

（1. 华北水利水电大学电力学院，河南省郑州市 450045；2. 中国水利水电科学研究院，北京市 100038；3. 中国长江电力股份有限公司，湖北省宜昌市 443002）

0 引言

电力变压器作为电力传输的重要环节，在电力系统中发挥着重要的作用［1］。国际上应用最广泛的变压器故障诊断技术是油中溶解气体分析（dissolved gas analysis，DGA）［2-3］。传统的油中溶解气体分析法包括三比值法、大卫三角形、罗杰斯比例、编码法等［4-7］。这些方法的识别结果偶尔会存在冲突或部分故障比例缺失，其灵活性需要优化。

当前，人工智能和机器学习在变压器故障识别领域已取得了较大的进展［8-10］，但这些智能算法自身也存在一定不足。例如，在样本数据较少时识别精度较低；面对大量高维数据时，容易出现过拟合、部分特征被忽略的情况；部分参数优化需要人为设置，影响了算法的客观准确性和普适性。此外，多数方法针对DGA 信息开展研究，忽视了变压器自身因素和外界条件所带来的影响。深度学习网络可以通过快速处理大量高维数据获取目标结果［11］，已有诸多学者利用深度学习网络进行变压器故障识别［12-13］。为进一步提高识别精度和效率，部分学者提出了深度残差网络，该网络利用特征快捷模块降低了参数优化的难度，网络中梯度的反向传递保证其识别特征的完整性［14-15］。但该网络面临噪声信号干扰下的表现较差，尤其是需要识别的特征参数较多时，网络会出现识别效果退化的情况［16-17］。因此，深度残差收缩网络（DRSN）被提出用于图像信号领域的含噪声识别［18］，该网络的特性能够满足DGA多气体分析的特点。

综上，本文研究利用深度残差收缩网络进行变压器故障识别。首先，为耦合变压器老化损耗和外界条件变化所产生的影响，本文构建了基于时序的特征气体向量作为网络输入。其次，本文构建可变软阈值消除原网络中的恒定偏差，提出浮动交叉熵函数降低误差在网络中的传递。所提模型的子通道阈值机制为每种气体设置了独立的故障阈值，该阈值可以随数据的不断输入自动更新，不依靠专家经验来设定阈值，同时也避免了以往阈值设置灵活适应性不足的情况。实验结果证明了所提模型对故障识别的有效性和故障预测的潜力。

1 子通道阈值的深度残差收缩网络

深度残差网络的层数过多会导致其无法处理更多非线性目标的映射及网络退化。且该网络被噪声或其他信号干扰时会影响网络的专注度和效率。深度残差网络的结构介绍见附录A。而深度残差收缩网络中的注意力机制能够从大量数据中有目的地筛选出需要的重要数据并聚焦于重要数据，忽略相对不需要或不重要的数据，即对不重要的特征进行剔除，对重要的特征进行保留。对某一故障，利用DGA 数据开展分析时，在该类故障中不发生变化的气体可视为噪声，或降低变化微弱气体的影响权重，这一特点使该模型亦适用于受潮故障（单特征气体故障，特征气体为H2；芳烃含量少的油“抗析气”较差，会产生微量CH4，但相比H2的体积分数变化可忽略不计）［1，5］。模型在识别绝缘受潮时，会忽略其他特征气体，提高对H2的专注度并获取针对性结果。后续识别绝缘受潮时，模型不需要对其他特征气体再进行专注性识别。此外，该网络可以实现梯度反向传播，并通过残差模块实现特征跨层传递［17］，网络中的软阈值机制能够有效去除噪声，提高特征识别精度［19］。子通道阈值深度残差收缩网络的部分模块和整体结构见附录A 图A1，软阈值的功能表示如下。

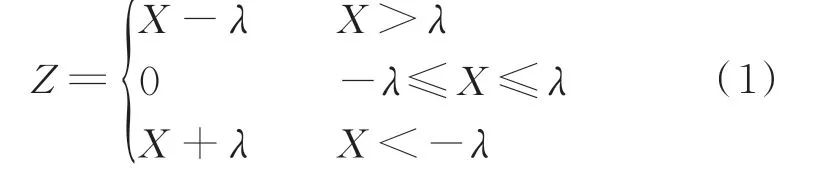
式 中：X为 输 入 特 征；Z为 输 出 特 征；λ为 正 参 数阈值。

子通道阈值机制的全局平均层是网络一个重要特点。因不同功能通道对诊断任务的贡献不同，注意力机制和全局平均池化层（GAP）对每个特征通道设置权重并调整特征通道输出的大小，实现对每个特征通道施加不同级别关注度的目的。GAP 在训练结束前计算通道数据，减少连接层的权重数量，并解决权重设置复杂和数据序列混乱的问题［20］。GAP 配合特征图的绝对值操作将高维输出变为一维形式，并传递到两个全连接层中，过程如下。

式中：zc为输出神经元的第c个特征；ac为第c个特征的尺度参数。

相应的阈值由以下方式确定。

式中：λc为第c个特征通道的阈值；ave(·)表示求平均 值 函 数；Xi，j，c表 示 第c个 宽 度 为i、高 度 为j的 输 入特征。

2 变压器故障识别模型

2.1 输入特征向量的构建

变压器油中气体体积分数与温度、负载、设备损耗和湿度等多种因素有关［21］。本文研究采用以DGA 全数据、温度、时间数据（基于时序的采样间隔保持一致）在时间窗口上滑动生成的连续特征向量作为网络的输入，见图1。图中表示在t时刻、正常温度下，7 种特征气体的体积分数。本文研究将温度添加到时序特征数据中，目的是使构建的输入数据能够耦合更多故障影响因素。温度分为正常（编码1）、低温过热（编码2）、中温过热（编码3）、高温过热（编码4）4 种状态。深度学习网络中的特征图是三维的，上述步骤给一维体积分数数据添加了标签，将其扩充为三维特征图的形式，网络对数据进行特征捕捉后降维输出。气体体积分数等同于图像中的特征通道，温度等同于图像的长度，时间等同于宽度，以保证数据形式符合图像信号的结构并满足网络对输入特征图的要求。

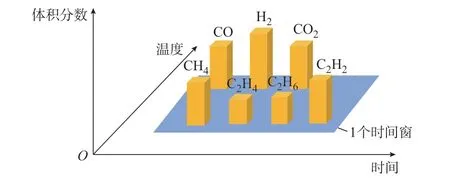
图1 输入气体的特征数据结构Fig.1 Structure of feature data for input gas

对数据集进行增强的方法包括数据样本增强和特征增强。数据增强是使用特定域的信息来增强源域和目标域数据的特征向量，并将其视为算法的新输入。之后，半监督学习分类器被应用于为源域有标签数据、目标域有标签数据和目标域无标签数据进行定义的特征映射。本文研究将温度检测结果添加至构建的特征图中，等同于为DGA 数据添加标签，使DGA 数据具备明显的温度特征，帮助网络捕获不同温度下DGA 气体的状态特征（体积分数分布和扩散速率）；且同一特征气体在不同温度下可能会出现不同的状态，加入温度标签后，网络对于过热放电混合故障的识别更高效。

在时序数据中，每个样本与之前的样本多存在某种依赖关系（变压器随着运行时间的增长出现老化，导致绝缘油有一定程度裂解，DGA 气体的特征分布也会发生变化，利用时序数据保证网络可以捕捉到变压器老化、负载变化所产生的影响特征），利用神经网络来处理这类数据，可以产生更高质量的样本和特征。本文研究向DGA 数据添加温度、时序标签，并结合网络的注意力机制，使模型能够更好地捕捉DGA 数据本身及其耦合的温度影响特征、绝缘老化特征、负荷特征等。此外，在机器学习中，避免网络出现过拟合的有效方法之一是对输入数据进行处理，为其添加更多的约束标签。特征增强及多维特征捕捉详细说明见附录B。

现阶段仍存在诸多标准外的变压器故障未被充分定义。因此，当有新型故障出现时，本模型的注意力机制也能捕捉到其异常特征，并尝试进行识别分类。在实际情况中，如果新投入的变压器或部分变压器因为故障检修导致数据量偏少，可以对原始数据进行扩充。为了最大程度上保证特征不变，扩充数据的选择优先级按照同类型、同运行条件进行，对各类故障样本进行等比均匀扩充。此外，将合适的含噪数据作为补充添加至原始数据集中也可以丰富数据集。扩充倍数适当便不会影响原始数据的特征分布［12］，或选择删除样本数量较少或不均衡的数据集，观察实验效果。

2.2 深度残差收缩网络的优化

因软阈值函数的渐近性不佳导致网络存在恒定偏差，即某特征气体体积分数值位于故障体积分数阈值边缘时，软阈值会强行将其置0 或1，促使网络将亚健康状态或潜在故障误识别为安全或故障。实际中，部分亚健康状态的变压器经过一段时间运行后会转为正常，而另一部分会演变为故障。为了消除恒定偏差，增强误识别状态和正确状态的区分度，本文研究构建可变软阈值替代网络中的软阈值。可变软阈值可表示为：

可变软阈值函数的连续性、渐近性和偏差分析见附录B。在此基础上，本文研究利用带回溯功能的快速软阈值算法解决因梯度下降导致计算效率低的问题并提高模型智能性，主要步骤如下。

优化目标可表示为：

式中：F(x)为最优目标函数；f(x)和g(z)分别为局部优化变量x的最优解和全局一致性约束变量z的最优解。

在变量z处的二次逼近函数QL(x，z)为：

式中：L为利普希茨常数；β为迭代步长的倒数；A和B表示任意常数；∇表示梯度因子；· 表示两个函数或向量的内积。

利用近端算式，将式（6）的最小值PL(z)缩写为：

忽略常数项对结果没有影响，则结合式（6）和式（7），最小值可写为：

根据上述方法进行迭代求解的步骤如下。

令利普希茨常数L（该常数依函数而定）的初值L0＞0，正实数η＞1，且x∈R，令z(1)=x0（上标（1）表示迭代次数，下同；x0为局部优化变量x的初值），步 长t1=1，搜 索 位 于Lˉ=ηik L(k-1)（Lˉ为L的 平 均值）中的最小非负整数ik。

式中：tk为第k次迭代的步长。

算法的迭代计算中，将前两次迭代的线性组合作为下一个逼近函数的起点能提高效率和智能性。

2.3 自适应可变权重的交叉熵函数

误识别会降低网络的训练效果。尤其在不同的识别误差下，网络最终的交叉熵损失却相同，这掩盖了网络对不同特征气体的真实权重。故本文研究提出对不同故障类型的特征气体附加一个可变的权重，该气体在某一故障中的影响因子越大且网络正确判断出故障时该气体的体积分数，则网络的交叉熵损失就越小［11］，交叉熵的定义为：

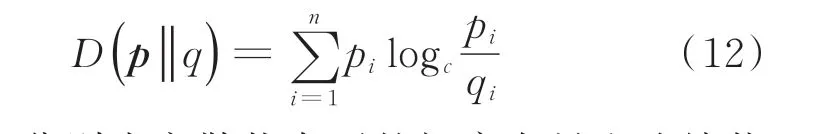
式中：p和q分别为离散状态下的概率向量和连续状态下的概率分布函数，pi和qi分别为对应的第i个元素。

利用模型识别n种故障的特征气体体积分数，每一种故障含7 种特征气体体积分数值，pm表示该故障下真实的特征气体体积分数值。假设识别误差遵循正态分布，用Pn(x)表示第n个故障下识别误差的概率密度函数，即

式中：μn为平均值；σn为方差。

则用P(x)代表某一故障下7 种特征气体的识别误差概率密度函数，即

式中：si表示支持向量s的第i个元素，即s=[s1，s2，…，sn]。

建立隶属度因子和优化目标关系，即

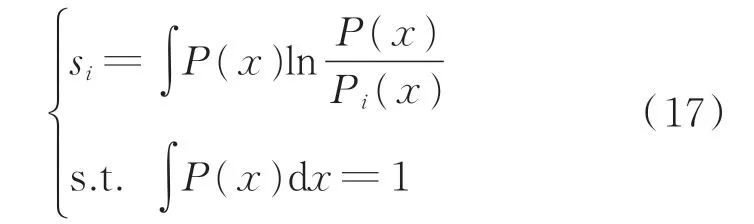
当两个函数的交集越大（识别的故障体积分数值与真实故障体积分数值越接近），可判定两个函数的支持度越高，隶属度因子越小。式（16）根据隶属度来确定不同特征气体对不同故障的影响权重系数。交叉熵最小（识别误差最低）目标函数为：

由式（18）可知，E表示支持向量s中元素的总和。随着s变小，相互支持度不断提高，这意味各气体体积分数关于判定故障权重系数的选择更加合理。

对于状态样本(ui，vi)，模型将其误识别为状态S的概率为pSi。利用构造的权重系数修正模型误识别导致的误差，则可变系数ξSi可表示为：

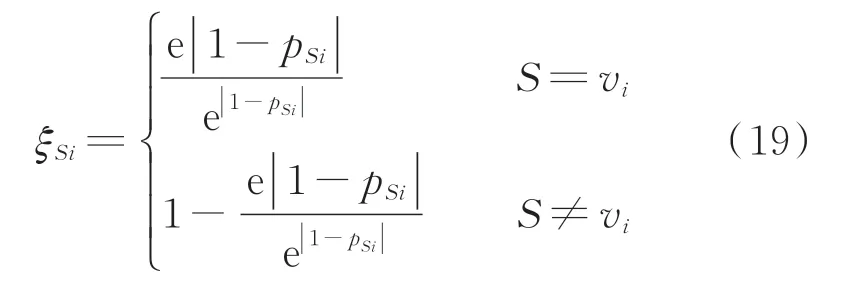
式中：S=vi和S≠vi分别表示模型识别的状态结果与实际的故障vi一致和不一致。

综合评价函数为：

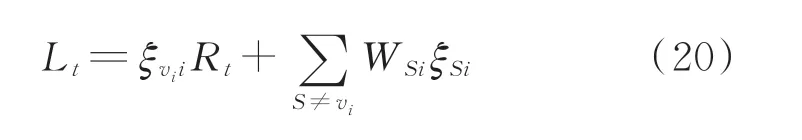
式中：Lt为综合评价损失；Rt为交叉熵损失；WSi为误识别损失。

变压器故障诊断流程如图2 所示。

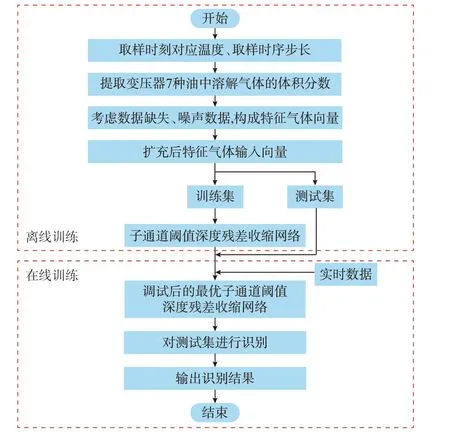
图2 变压器故障诊断流程图Fig.2 Flow chart of fault diagnosis for transformer

3 实验与分析

利用实验收集数据和IEC 数据集来验证该模型的有效性。

3.1 实验数据与超参数设置

本文研究的原始数据源于某电厂的6 台变压器油中气体监测数据。数据跨度从2017 年5 月29 日至2020 年3 月1 日，考虑到变压器因检修等原因导致样本数量不均衡，本文研究从IEC TC10 数据库收集数据来丰富样本，共计8 400 条样本数据。样本数据具体分布见附录C 表C1 至表C4。采集的部分温度及DGA 数据见图C1 至图C3。将数据分为训练集和测试集。每个数据集分为10 个子集，包含9 个训练集和1 个测试集，采用交叉验证法保证每个子集都能被训练并捕捉特征。数据扩充所添加的噪声信号的e 值需根据实际效果设置，过大会影响数据的特征分布。本实验采用Python 建立网络模型，实验运行环境是搭载i7-9750 中央处理器和NVIDIA Geforce GTX 图像处理器的计算机。本文研究根据场站要求，将绝缘受潮等状态纳入亚健康状态，并根据IEC 标准对变压器状态进行分类，见表C5。

由于DGA 数据稳定性较差，且提取数据时对时效性要求高。现阶段的解决方法多是加强传感器的精度和监测频率。本文研究使用VALSALA 光学气体测量装置技术获取DGA 数据。该设备能实时快速地采集数据，避免气体之间的相互干扰和再次溶于油中带来的误差，同时提供变压器油温数据。新模型可嵌入该设备的自诊断模块中运行。

输入特征向量的结构为C×W×I，其具体设置为：气体种类数C设为7，本文研究识别7 种特征气体的体积分数，故特征通道数为7；W为温度，按2.1 节代码分别设为1（正常）、2（低温）、3（中温）和4（高温）；I表示时序数据采样点数，该数值设置根据电厂监控设施的采样频率决定，采样点数为采样频率的倒数。深度残差收缩网络的层数和卷积核数的设置没有最佳标准。因此，本文研究根据常用建议进行设置［22-23］。在训练过程中，网络的训练率将按照时间设置，前30 个时期、中间30 个时期、最后40 个时期的训练率分别为0.1、0.01、0.001，目的是获取最佳的输出结果并确保参数更新在下一次训练开始前完成。同时，向目标函数中添加惩罚项与L2正则化避免过拟合，惩罚系数设置为0.001［24］。网络结构基于ResNet34 框架搭建。本模型采用不同框架的迭代训练结果见附录D 表D1，具体残差模块见表D2。网络最终输出层具有9 个神经元，表示1 个正常（亚健康状态）和8 个故障状态。

3.2 案例学习与分析

为验证改进软阈值函数的去噪效果，将不同信噪比的高斯白噪声和拉普拉斯噪声添加到原始信号并进行去噪操作。原始信号由MATLAB 仿真获得。去噪效果见附录E 图E1 和图E2，信噪比与均方差见表E1。结果显示，改进后的软阈值函数对两种噪声信号均有良好的适应性，经过去噪后的信号波形更平顺，相比于软阈值，新函数能更好地保留原始信号的特征。这证明添加适当的噪声信号不会改变原始数据的特征。对比表E1 中数据发现，改进后的软阈值函数信噪比至少比硬阈值和软阈值分别高出0.81 和1.47，均方差相比两者分别降低了0.06 和0.12。该结果验证了本文研究提出的可变软阈值拥有更好的去噪效果，能够降低因局部最优解而强制忽略边缘解产生的误差。

利用本文的网络（改进的深度残差收缩网络（IDRSN））与DRSN 和卷积神经网络（ConvNet），对不同样本数量下电弧故障进行识别对比，其识别精度见表1，模型对其他类型故障在不同样本数下的识别精度见附录E 表E2。3 种方法对含噪信号的识别精度见图3 与图4。

表1 不同样本数量下的识别精度Table 1 Recognition accuracy with different sample sizes

由图3 和图4 可知，与其他两种网络相比，改进后的网络有更高的识别精度和抗噪能力。该模型在小样本下的识别精度可达到96.84%，当样本数量增加到150 时，其训练精度可达到99.25%。随着样本数量的增加，该模型的识别精度亦显著增长，同时也验证了数据扩充对提高模型识别精度的有效性。

图3 网络训练精度Fig.3 Training accuracy of network

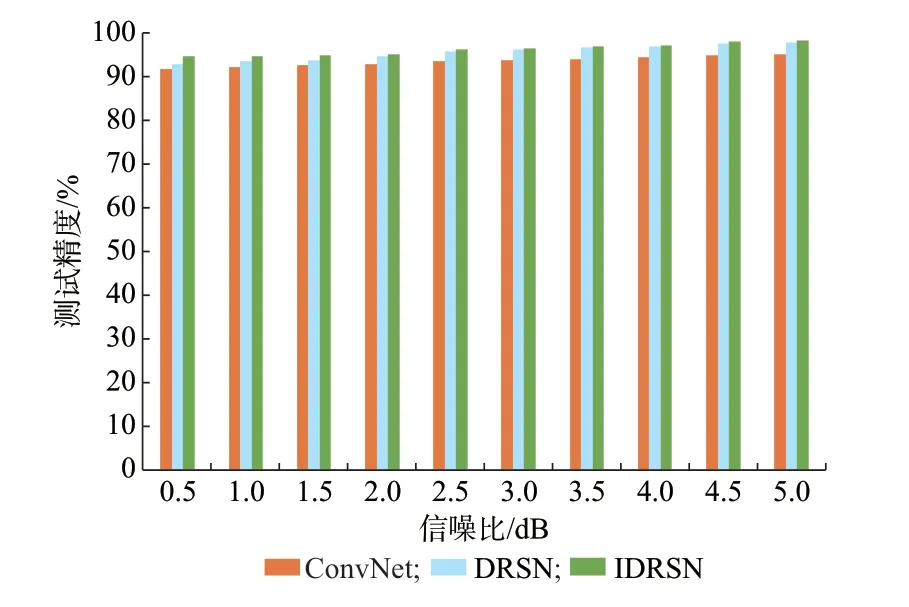
图4 网络测试精度Fig.4 Testing accuracy of network

表2 展示了可变权重交叉熵函数对降低模型识别误差的效果。附录F 表F1 给出了误识别分析结果，权重设置及误差分别见表F2 和表F3。

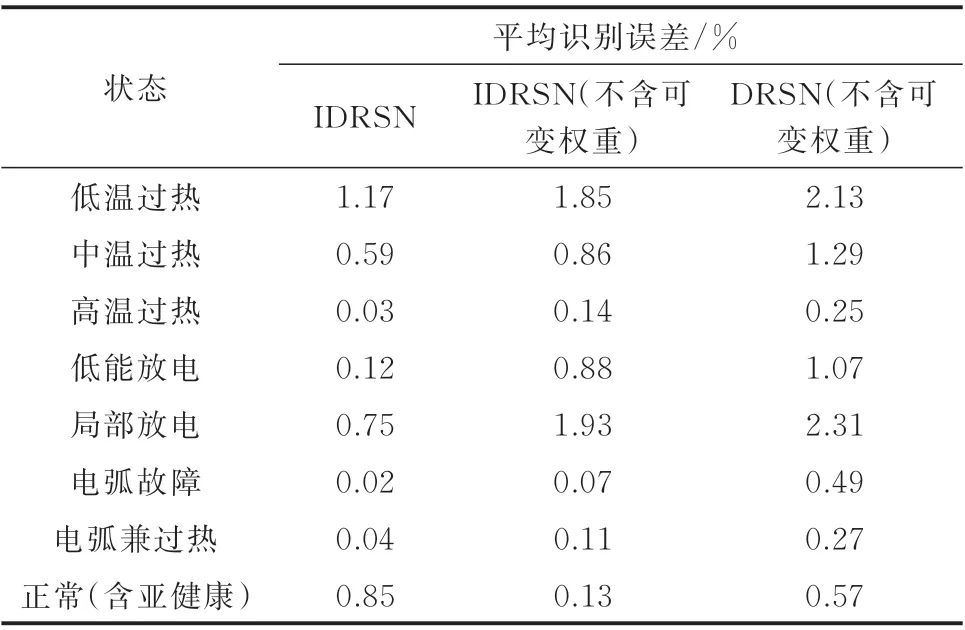
表2 不同类型故障的识别误差Table 2 Identification errors of different types of faults

在实验中发现，模型对CO 和CO2进行故障判断时，误差相对较高。这是因为这两种气体在空气中含量较高，而且受非故障因素影响较大。采用可变交叉熵权重赋值的模型判断样本所属状态，当模型经过学习判定该气体与故障的关联越大，则权重越大，该样本被识别为正确状态的概率亦越高，那么损失权重值就越低，增强了正确识别与误识别的区分度，减小了误识别带来的误差对网络产生的影响。

3.2.1 案例学习1

支持向量机（SVM）、反向传播神经网络（BPNN）、卷积神经网络是最为常用的变压器故障智能诊断技术［25-27］。其中，SVM 算法的性能取决于其核函数及其参数的选择。为了保证SVM 算法能够展现良好性能，SVM 中核参数设置为8.41，惩罚因子设置为1 000，停止训练误差设置为0.001；BPNN 隐含层神经元个数为10，输出9 个神经元，输入和输出传递函数均采用sigmoid 函数；卷积神经网络设置与本模型一致［28-29］。利用5 种模型对变压器DGA 状态数据进行识别，识别精度如表3 所示。

表3 变压器不同故障类型识别精度的比较Table 3 Comparison of identification accuracy of transformers in different states

由表3 中数据可知，本文研究提出的方法相对识别精度更高，平均识别精度可达到99.71%，与其他常用故障识别方法相比精度高出4%～10%。证明了本文研究提出的方法能够有效处理复杂的高维特征数据。所提模型不依靠专家经验设置阈值仍保证了较高精度，

3.2.2 案例学习2

为进一步验证本文方法的实际应用效果，将常用的三比值法和大卫三角形分别与SVM 和贝叶斯网络进行组合［30］，与本文研究提出的故障识别方法进行对比（样本数据均为同一组数据，按照各方法需求对其进行比值处理）；选取深度置信网络（DBN）和门控循环网络（GRU）对全DGA 数据进行故障诊断。GRU 层的隐藏层单元数取值范围为50、最大训练周期取值范围为100、分块尺寸取值范围为50、学习率取值为0.000 01。DBN 设置网络的学习率为0.01，训练批次为5，动量值为0.05，激活函数为sigmoid 函数。迭代次数综合考虑识别能力和训练时间等最终设为150 次［31-33］。模型组合依据及参数设置见附录G，测试结果见附录H 表H1。

根据附录H 表H1 中数据可知，基于大卫三角形的贝叶斯网络故障识别和基于改良三比值法的SVM 在识别精度上都低于本文研究所提出的方法。利用改进的深度残差收缩综合DGA 数据三比值法的识别精度亦低于本文研究所提出的方法。因为事故前期，DGA 的体积分数未达到故障比值时（不同气体扩散速率存在差异），网络无法做出判断。从中国长江流域某水电站中采集的故障数据显示，绝缘潮湿导致变压器发生事故时，基于三比值的故障识别方法往往不能诊断出早期故障特征。本文研究将绝缘潮湿纳入亚健康状态中，提高工作人员的重视程度，与微水监测配合避免因绝缘受潮引发严重事故。进行过热分析时，本文研究将CO 和CO2纳入特征气体，能够识别出过热（低温）故障的具体类型，即CO 体积分数下降伴随CO2上升多是因裸金属过热和固体绝缘过热导致，有助于工作人员缩小故障范围。而采用三比值法进行判断时，偶尔会出现0-0-1、0-2-1 和0-2-2 等故障编码组合导致误判发生，且比值法中不包含CO 和CO2的比值判定。尤其是部分开放式变压器，在利用三比值法进行分析时，需要对比值结果进行修正，增加了识别难度。对于深度置信网络，其在单层时识别效果较好，但当玻尔兹曼机层数增加时，会导致误差和特征一起传递给下一层影响最终的识别精度。GRU 作为长短期记忆网络模型的变种，无法对上一时刻的状态进行学习，而且在大量时序数据集的情况下，GRU 的表现有所下降。

此外，基于比值法的故障识别技术存在比值组合缺失的情况，这些因素导致一些发展阶段的故障往往被忽略。当某种气体体积分数超出正常体积分数一定范围时，本文研究提出的故障识别方法可以更好地捕捉异常数据。

4 实际应用

利用本文研究提出的故障识别方法对国家电网某公司变压器故障进行监测，本模型及设备接入电站变压器，同时场站监控系统也提供实时数据。本模型在上午08：30 发出警报信号，提示3 号变压器内部存在低能放电、过热和电弧故障。但场站监测系统一直未发出报警信号，直至16：30，该变压器由于重瓦斯保护跳闸。事后，工作人员分析了变压器内部油色谱数据发现变压器内部发生了电弧故障，具体故障数据如表4 所示。

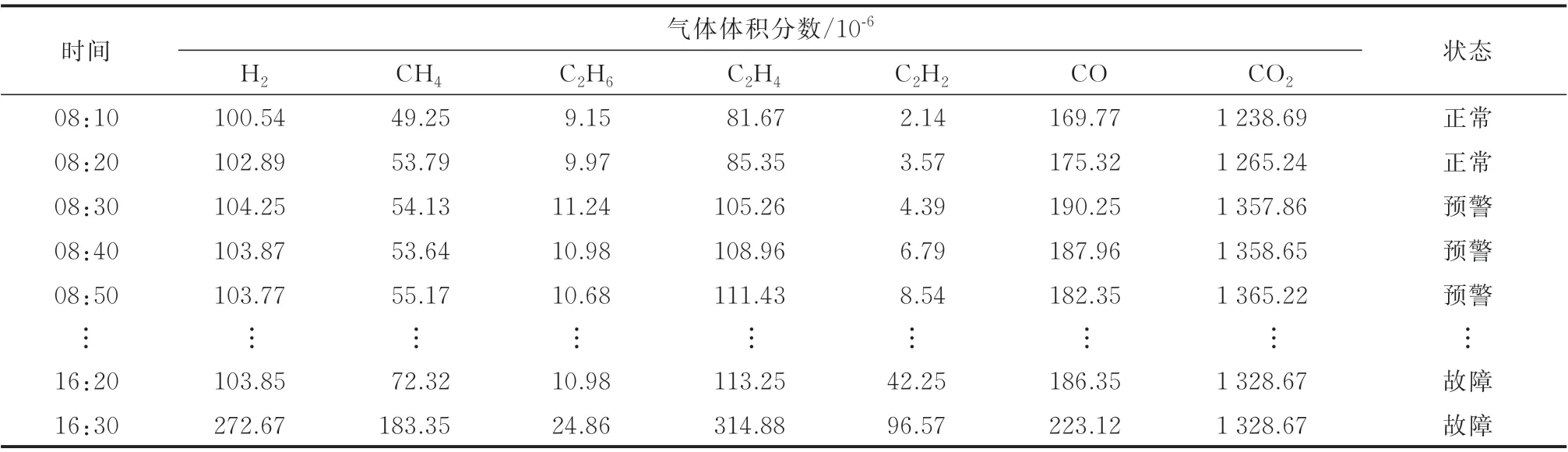
表4 特征气体体积分数的趋势Table 4 Trend of feature gas concentration

从表4 中可知，本文研究提出的故障识别方法在发出报警信号时，变压器内部故障已经出现且处于快速发展阶段。但是在事故初期，气体体积分数不能满足三比值法的体积分数要求，导致其他两种方法没能辨识出高温过热和电弧放电故障的前兆。同时，电站的监测设备将故障视为低能放电（0-2-1），致使工作人员未能重视变压器异常状态，最终导致变压器发生跳闸。

模型在运行过程中出现将亚健康状态识别为故障状态的情况，不能完全将其视为误识别，这也提示应该避免让变压器长时间处于亚健康状态运行，一旦突破临界，变压器发生严重事故的概率就会增大。虽仍面临神经网络的通病“黑盒”，但通过对网络优化改进，模型的注意力机制以及对新、旧数据特征的反复学习能够有效降低识别误差。而且，随着样本数量的扩大，模型的智能性会使识别结果更佳。

5 结语

本文研究引入图像识别领域的深度残差收缩网络并对其优化改进，与新构建的仿图像化特征输入向量配合完成变压器故障识别。通过实验分析得到以下结论。

1）新构建的特征输入向量能耦合多种故障影响特征，解决仅依靠DGA 数据或比值数据导致结果冲突、编码缺失、故障类型不全面的问题。

2）新构建的可变软阈值函数和交叉熵函数能有效降低网络的恒定偏差和识别误差。与特征输入相配合能够增强对数据特征的学习能力，提高特征提取的完整性。

3）新模型能够自动更新故障特征阈值，智能程度高，且相比于现有方法具备更高的识别精度及鲁棒性。此外，模型对IEC 标准外的新型故障有良好的适应性。

此外，故障检修后重新投入运行的变压器偶尔会出现轻瓦斯故障，需进行放气，这导致实时DGA数据出现波动，影响模型判断。对此，本文研究认为需要提高硬件设备的精度或进行图像诊断技术的研究。当网络结构的复杂程度提高时，计算效率会出现小幅下降，后续研究会对网络继续优化。随着光声光谱及光学成像等技术的发展，本文研究提出的方法在硬件配合下会有更好表现。此外，本文研究提出的方法对故障预防有着良好的效果和拓展性，与循环神经网络组合可以开展预测研究；对暂态数据或频率、电压、波形等数据进行分析可以判断电网暂态稳定性及电能质量。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。