自旋为1/2 的双层平方晶格阻挫模型的基态相变*

卿煜林 彭小莉 文林 胡爱元

(重庆师范大学物理与电子工程学院,重庆 401331)

基于线性自旋波理论,研究了二维各向异性双层平方晶格阻挫模型的基态性质.探讨了各向异性和自旋间交换作用对基态相图及系统可能发生相变的影响.结果显示:对于各向同性,当层间耦合相互作用Jc ≥0.21 或 Jc ≤-0.175 时,Nèel 态(NS)和Collinear 态(CS)能共存;对于各向异性,NS 和CS 也可以共存.对弱的各向异性,NS 更稳定;对于强的各向异性,系统将发生由NS 向CS 转换的一阶相变.

1 引言

由于阻挫模型中最近邻和次近邻交换作用之间的相互竞争,导致系统出现了一些新奇的相,因此在过去30 年里,海森伯阻挫模型已被广泛的研究.其中最著名的例子是自旋为1/2 的二维平方晶格阻挫模型,也称J1-J2模型[1-13],其哈密顿量为

其中J1和J2分别描述的是自旋间最近邻和次近邻交换作用参数.〈i,j〉和〈〈i,j〉〉分别表示的是对最近邻和次近邻格点求和.目前这个模型的基态性质已经被很好地理解:当α＜α1～0.4(α=J2/J1)时,系统是Nèel 态(NS),即最近邻自旋取向反平行,相应的波矢为Q(π,π);当α＞α2～0.6 时,系统是Collinear 态(CS),即最近邻自旋取向沿x(y)轴取向平行(反平行),沿y(x)轴取向反平行(平行),其相应的波矢为Q(0,π)和Q(π,0),系统是二重简并;当α1＜α＜α2时,系统对应的是一个顺磁相[1-13].

该模型的重要性还体现在实验上制备出的化合物,如LiVO(Si,Ge),VOMoO4和BaCdVO(PO4)2,可以采用该模型来描述其磁性质[14-16].需要指出的是:实际材料一般是层状结构,完全忽略层间耦合的可能性极小.因此,理论研究一般需要考虑层间耦合相互作用才能更好地描述化合物的磁性质,这在以往的研究中已经得到了证实[17-20].

众所周知,量子磁体的相变性质是依赖晶格维度的.对于二维平方晶格的J1-J2模型,当引入层间耦合相互作用后,其顺磁相会随着其耦合强度的增强而消失.目前众多理论,如:团簇平均场近似[21]、旋转不变格林函数和耦合团簇方法[22]、有效场理论[23]、自旋波理论[20,24,25]、系列展开法[26]、分层平均平均场方法[27]、耦合团簇方法[28]等,给出了层间耦合相互作用在0.12—0.6 范围内取值时,顺磁相消失.同时,这些研究发现:当层间耦合参数值大于无序相消失所对应的值时,NS 与CS 出现了重叠,这意味着在重叠区域NS 和CS 皆是系统可能的态,即NS 和CS 可以共存.一个自然的问题是:共存区域内哪个态更稳定呢? 目前还没有研究回答这个问题,需要进一步的研究.

基于上述问题,本文采用自旋波理论,以自旋为1/2 的双层平方晶格阻挫模型为研究对象,探究零温下不同态重叠时哪个态更稳定.考虑到实际材料存在各向异性,模型引入了交换各向异性.同时注意到研究多考虑层间耦合为反铁磁交换作用[21-27],对其铁磁交换作用的研究相对匮乏[28].因此本文将全面探讨这两种层间耦合相互作用对系统相变性质的影响.

2 模型与方法

图1 描述的是NS 和CS型基态磁结构,其中图1(a)和图1(b)对应层间耦合为反铁磁交换作用,图1(c)和图1(d)对应的是层间耦合为铁磁交换作用.实心和空心圆圈分别描述的是磁性离子自旋取向向上和向下.从图1 可以看出,无论是NS型还是CS型,自旋向上和自旋向下的磁性离子数目相等.为了方便,将晶格分成两个子晶格,即自旋取向相同的为一子晶格,分别采用阿拉伯数字1 和2 来标识这两个子晶格.本文采用线性自旋波理论推导系统磁化强度和基态能的解析表达式.由于推导4 种磁结构的过程过于冗繁,因此本文以图1(a)为例,给出其具体推导,其他3 种磁结构的推导不再赘述.图1(a)模型的哈密顿量为

图1 NS 和CS 的磁构型 (a),(b)层间耦合为反铁磁相互作用;(c),(d)层间耦合为铁磁相互作用.实心和空心圆圈分别描述的是自旋取向相上和向下Fig.1.Spin configurations of the NS and CS:(a),(b)Interlayer coupling as antiferromagnetic interactions;(c),(d)interlayer coupling as ferromagnetic interactions.The solid and empty circles represent the up-spins and down-spins,respectively.

式中 [i,j] 表示对层间最近邻格点求和.Jc为层间耦合交换作用参数.η是交换各向异性参数,其取值范围为 0≤η≤1.当η=0 时,模型退化为Ising 模型.显然,η值越小交换各向异性越强.选z轴为量子化轴,则子晶格磁化强度定义为自旋算符的统计平均,即:.无外场时,它们之间存在如下关系:m=m1=-m2.

根据自旋波理论的一般步骤[29],首先采用Dyson-Maleev 变换[30],将哈密顿量(2)式映射成一个等价的玻色相互作用的哈密顿量,即:将哈密顿量中的自旋算符采用玻色湮灭算符和产生算符来表示,具体形式如下:

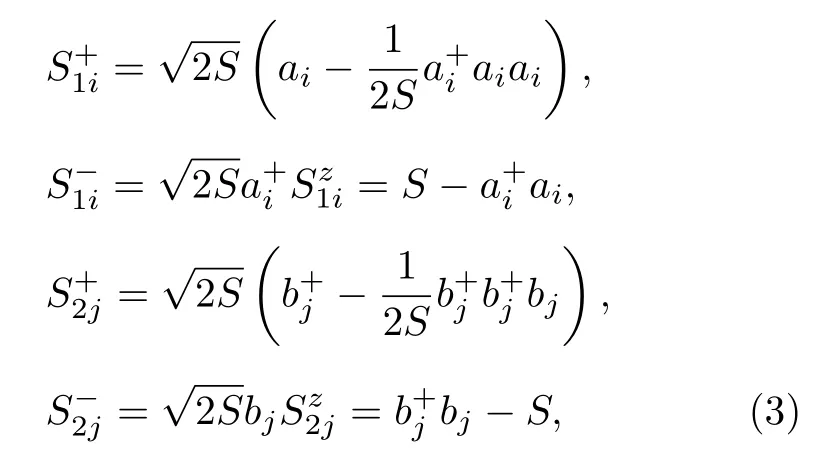
将方程(3)代入(2)式得

其中z1,z2和zc分别为最近邻、次近邻和层间最近邻格点配位数.对于线性自旋波理论,(5)式忽略了算符的四次项.然后对玻色算符进行空间傅里叶变换,即将坐标空间的哈密顿量转换到动量空间.傅里叶变换形式如下:

式中,N是晶格格点数.对波矢k求和遍及第一布里渊区.将(6)式代入(5)式,得到了一个非对角的哈密顿量.接下来采用博戈留波夫变换对动量空间的哈密顿量进行对角化,即:

这里αk和βk是玻色算符.对角化后的哈密顿量可以表示为

其中,

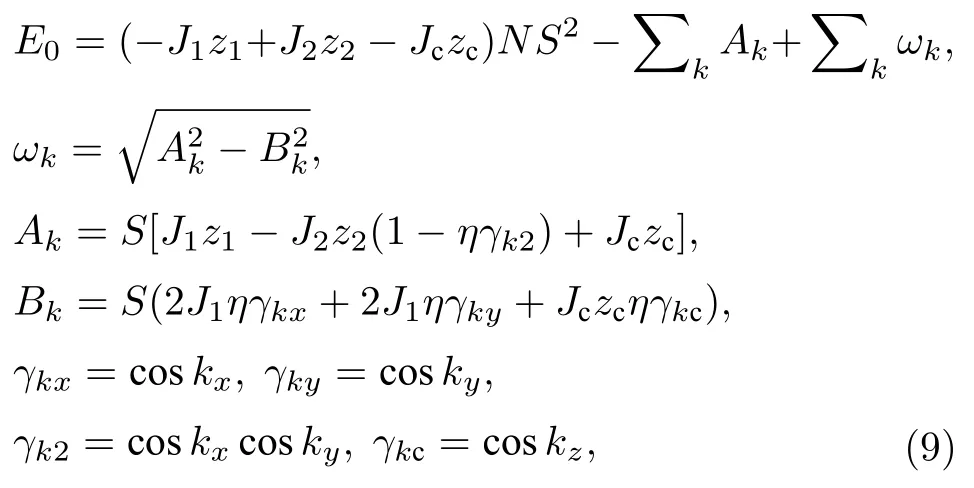
这里E0是系统基态能.γkx,γky,γk2和γkc是晶格的结构因子.

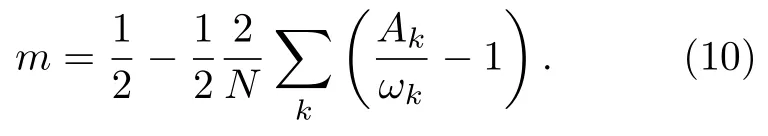
3 结果与讨论

首先讨论各向同性的情况,即:η=1.图2 显示了各向同性时,不同Jc值下磁化强度m与J2之间的变化关系,其中图2(a)和图2(b)分别对应Jc≥0 和Jc≤0.对于确定的J2,m随着|Jc|的增大而增大.这是因为,当|Jc|从0 开始增大时,不仅增多了最近邻键的数目,而且也增大了其强度,使得系统更加有序.对于确定的|Jc|,NS 的m随着J2的增大而减小,而CS 的m随着J2的增大而增大.这是因为,当J2=0 时,哈密顿量描述的是一个普通的反铁磁体,即NS.当J2从0 开始增大时,系统引入了阻挫,J1和J2之间出现了相互竞争,且它们之间的相互竞争强度随着J2的增大而变得越加激烈,这使得系统更加无序.对于Jc=0 ,竞争在J2=0.378 时(由于已经取J1=1,此时J2的值实际上是 0.378J1)达到最大,于是系统将从有序态向顺磁相转变.当Jc≥0.21 或Jc≤-0.175 时,此时竞争皆在J2=0.5 达到最大.在这种情况下,当|Jc|进一步增大时,J1和J2之间的相互竞争开始减弱,导致系统更有序,此时系统对应的是CS.对比Jc＞0 和Jc＜0 的结果(见图2(a)和图2(b))发现:在Jc相等的条件下,后者的磁化强度要大于前者.这主要是由于反铁磁交换作用的量子扰动大于铁磁交换作用,导致前者更容易无序.

图2(c)和图2(d)对比了不同方法得到的m与J2的关系.由图2(c)可知,当Jc=0 时,SE I,SE II和CCM 的结果彼此符合较好,表明这3 种方法得到的结果是可靠的.当J2值较小时,这5 种方法得到的结果一致.尽管对于大J2值,本文结果与其他4 种方法存在较大差异,但在一些参数值下,本文结果与SE I,SE II,CCM 仍然一致.对比LSW 与SOSW 的结果表明高阶关联校正是显著的.分析认为,SOSW 考虑了自旋波之间的相互作用,因此对仅考虑非相互作用自旋波的LSW 带来了一些修正.当Jc=1 时,本文与SE II 结果一致,见图2(d).

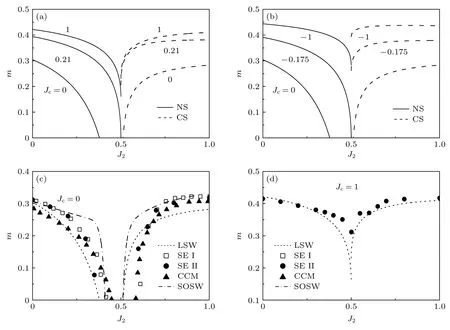
图2 当 η=1 时,不同 Jc 下的子晶格磁化强度 m 与 J2 之间的关系 (a)Jc=0,0.21,1;(b)Jc=0,-0.175,-1;(c)Jc=0;(d)Jc=1 .图(c)和(d)中,短划线、空心方格、实心圆、实心三角形和破折号分别描述的是线性自旋波理论(本文的结果,LSW)、系列展开法到9 阶(SE I)[31]、系列展开法到12 阶(SE II)[26]、耦合团簇方法(CCM)[31]和二阶自旋波理论(SOSW)[32]的结果Fig.2.Sublattice magnetization m as a function of J2 for different Jc values at η=1:(a)Jc=0,0.21,1;(b)Jc=0,-0.175,-1;(c)Jc=0;(d)Jc=1 .In panel (c)and (d),the shorted-dashed lines,open squares,filled circles,filled triangles and dashed-doted lines represent the results of the linear spin wave (this paper,LSW),the series expansion up to the 9th order (SE I)[31],the series expansion up to the 12th order (SE II)[26],the couple-cluster method (CCM)[31] and second-order spin wave (SOSW)[32],respectively.

为更清楚理解参数J2与Jc对系统相变的影响,图3 显示了模型在J2与Jc参数空间中的相图.从图3 可以看出,相图被分成了3 个区域,即NS,CS和顺磁相.由于层间耦合相互作用抑制了系统的顺磁相,导致顺磁相区域随着|Jc|增大而减小,并在=0.21 或-0.175 时完全消失,此时NS 和CS 的相变点在(,J2=0.5)处汇合.对比其他理论结果,本文=0.21 的结果与二阶自旋波理论(=0.3)[25]、耦合团簇方法(=0.2—0.3)[22]、分层平均平均场方法(=0.28—0.3)[24]和系列展开方法(=0.54±0.03,J2=0.16±0.03)[26]的结果一致.尽管如此,与自洽自旋波方法(≈0.25)[20]、团簇平均场理论(=0.12)[21]和有效场方法(=0.67)[23]存在较大的差异.对于本文=-0.175的结果则偏离了耦合团簇方法(=-0.45,J2=0.547)[28]的结果.当|Jc|≥时,NS 和CS 在J2=0.5处重叠,这意味着NS 和CS 皆是系统可能的态,它表明NS 和CS 在这种情况下可以共存.

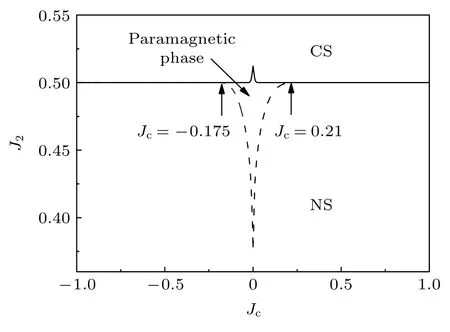
图3 当 η=1 时,系统在参数 J2 和 Jc 空间的基态相图Fig.3.Ground state phase diagram in the J2-Jc plan for η=1.

接下来讨论各向异性的情况,即:η/=1.图4显示了不同η,Jc值下磁化强度m与J2之间关系.从图4 可以看出,当Jc=0 时,系统顺磁相区域随着各向异性的增强而变小,当η=η1=0.956 时两个态在J2=0.488 处重叠,见图4(a).这是因为各向异性抑制了系统的扰动,导致系统更有序.最近蒙特卡罗模拟的结果显示:在Ising 极限下,即:Jc=0,η=0,系统在J2/J1=0.5 是简并的,但此时系统并没有出现无序相[33].这意味着,当η＜η1时,无论Jc取何值,系统将不会出现顺磁相.如果η＞η1,要想使顺磁相消失,Jc必须取有限值,见图4(b)和图4(c).图4(a)—(c)结果表明:存在一组(η,Jc)值对应着系统有序与无序的分界线.图4(d)显示了当Jc=0.3 时,不同η值下m与J2之间的关系.它呈现出3 个特征:1)两个态的磁化强随着各向异性(η越小,各向异性越强)的增强而变大,其原因已在图4(a)进行了说明;2)当η=0 时,两个态的磁化曲线完全重合,且磁化强度是饱和的.这是因为在这种情况下,两个态退化成一个普通的Ising 模型,系统没有横向关联.因此,在零温,系统磁化强度趋于饱和;3)当η＜1 时,两个态的磁化强度曲线开始出现重叠.当各向异性增强到一定程度时,其曲线交叉,且交叉区域随着η值的减小而变大.这是因为η的减小,系统各向异性的增强,它抑制了自旋沿XY方向的阻挫,系统有序度增强[34].因此,当η减小时,两个态的磁化强度变大,其曲线的交点也随之提升,其相应曲线交叉区域变大.当各向异性变弱时,曲线交叉区域消失.

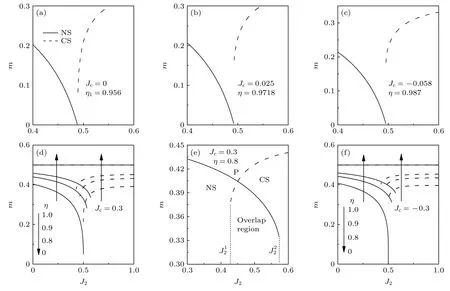
图4 不同参数时的磁化强度 m 与 J2 的关系 (a)Jc=0,η=0.956;(b)Jc=0.025,η=0.9718;(c)Jc=-0.058,η=0.987;(d)Jc=0.3,η=0.8;(e)Jc=0.3,η=0.8;(f)Jc=-0.3,η=0,0.8,0.9,1Fig.4.Sublattice magnetization m as a function of J2 for different parameter values:(a)Jc=0,η=0.956;(b)Jc=0.025,η=0.9718;(c)Jc=-0.058,η=0.987;(d)Jc=0.3,η=0.8;(e)Jc=0.3,η=0.8;(f)Jc=-0.3,η=0,0.8,0.9,1.

为了更清楚地显示出两个态的磁化曲线交叉,图4(e)显示了当η=0.8,Jc=0.3 时的放大图.可以看出,平面分成了4 个区域,即NS、CS、顺磁相P 和NS 与CS 的重叠区域.它显示:当J2≤时,系统对应的是NS;当J2≥时,系统对应的是CS;当时,NS 和CS 皆是系统可能的态,即在这情况下NS 和CS 可共存.图4(f)显示的是Jc＜0 的情况,其结果与Jc＞0 的情况完全类似.

为了更好地理解 (η,J2,Jc)这一组参数对两个态共存的影响,图5 在参数η和Jc空间内给出了两个态共存所对应的区域.可以看出,平面分成了两个区域,一个是顺磁相区域,另一个是NS 和CS共存区域.实线是系统有序-无序分界线.这里需要指出的是:当η=1 时,两个态共存所对应的J2值是0.5,如图3 所示;而当 0≤η＜1 时,J2在范围内取值时,两个态共存,如图4(e)所示.

图3—图5 显示了在一定条件下,两个态可以共存.一个自然的问题是:在共存区域,两个态中哪种状态更加稳定呢? 接下来将详细回答这个问题.根据热力学理论,在零温,内能低的态更稳定.

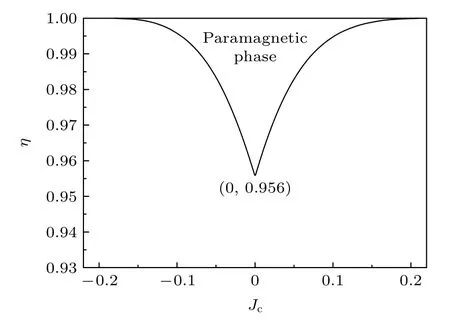
图5 在参数 η -Jc 空间中两个态共存所对应的区域.平面分成了两个区域:顺磁相和两个态共存的区域.在共存区域 J2 的取值范围是 .相应的例子是图4(e)Fig.5.Area corresponding to the coexistence of the two states in the η-Jc space.The plane is divided into the two areas:paramagnetic phase and the coexistence of the two states.In the coexistence area of the two states,the value range of J2 is .The corresponding example is Fig.4(e).

对于η=1,系统在 |Jc|≥时,NS 和CS 在J2=0.5处重叠.图6(a)给出了在这种情况下,两个态的基态能E0与Jc的关系.从图6 可以看出,NS的基态能始终小于CS,即对于各向同性系统,NS更稳定.图6(b)显示了在Jc=0 和1 时LSW 与SE II[26]的基态能E0与J2的关系.它显示了在这两种情况下,LSW 与SE II 的结果完美一致.

图6 (a)当 J2=0.5 时,NS 和CS 的基态能 E0 与 Jc 的关系;(b)当 Jc=0,1 时,NS 和CS 的基态能 E0 与 J2 的关系.实心方块和实心圆是系列展开法(SE II)的结果[26]Fig.6.(a)Ground state energy E0 of the Néel and collinear states as a function of Jc for J2=0.5 ;(b)ground state energy E0 of the Néel and collinear states as a function of J2 for Jc=0,1 .The filled squares and filled circles are the results of the series expansion up to the 12th order(SE II)[26].

对于η＜1,两个态在范围内共存.图7显示了在这种情况下,Jc=0.03 时,不同η值下系统基态能E0与J2的关系.从图7(a)可以看出,当各向异性很弱时,即η=0.97,NS 的基态能小于CS,即NS 更稳定.随着各向异性增强,NS的基态能随着J2的增大而变大,而CS 的基态能随着J2的增大而变小.当η=0.7703 时,两个态基态能在汇合,即的范围内,EAF1＜EAF2,表明NS 更稳定,见图7(b).在J2=处,系统可能是NS,也有可能是CS,或者两者共存.当η＞0.7703时,两个态的基态能曲线开始出现相交,见图7(c)和图7(d).为了方便,令交点所对应的J2标识为.当J2＜时,EAF1＜EAF2,即NS 更稳定;当J2＞时,EAF1＞EAF2,即CS 更稳定.在J2=时,系统将发生由NS 向CS 转换.由于此时两个态磁化强度曲线的交点所对应的J2值为0.436,它不等于=0.52,这意味着系统由NS 向CS 转换所对应的磁化强度变化不连续,表明这两个态之间的相转换为一阶相变.对于强的层间耦合(在这里没有呈现其结果),其结果与弱的层间耦合完全类似.

图7 当 Jc=0.03 时,不同 η 值下两个态的基态能 E0 与J2 的关系 (a)η=0.97;(b)η=0.7703;(c)η=0.5;(d)η=0Fig.7.Ground state energy E0 of the two states as a function of J2 for different η values when Jc=0.03:(a)η=0.97;(b)η=0.7703;(c)η=0.5;(d)η=0.

图8 当 时,两个态的基态能在参数 Jc-η空间中的比较Fig.8.Comparison of the ground state energy of the two states in the Jc-η space when .

4 结论

本文基于线性自旋波理论,研究了二维双层平方晶格海森伯阻挫模型的基态性质.探讨了各向异性与层间耦合对系统基态相变的影响.结果显示:对于η=1,当Jc≥0.21 或Jc≤-0.175 时,NS 和CS 在J2=0.5 处可以共存.当η＜1 时,两个态在范围内也可以共存.因此,本文探讨了在这两种情况下,NS-CS 之间的稳定性以及它们之间可能发生的相变.结果显示:对于η=1,NS 的基态能始终小于CS,即在这种情况下系统的状态是NS.对于η＜1,在范围内,参数η和Jc对两个态基态能的影响可以分成两个区域,即图8 中的区域B 和区域C.在区域B,NS 的基态能始终小于CS,即此时系统的状态是NS.在区域C,当J2＜时,EAF1＜EAF2,此时系统的状态是NS;当J2＞时,EAF1＞EAF2,系统的状态是CS.在J2=时,系统将发生由NS 向CS 转换的一阶相变.