一种基于标记单光子源的态制备误差容忍量子密钥分发协议*

马啸 孙铭烁 刘靖阳 丁华建 王琴†

1)(南京邮电大学,量子信息技术研究所,南京 210003)

2)(南京邮电大学,宽带无线通信与传感网技术教育部重点实验室,南京 210003)

在实际量子密钥分发系统中,由于设备、器件存在缺陷,在量子态制备过程中往往存在误差,而这些态制备误差会导致一定的系统安全性漏洞.本文在Tamaki 等(Phys.Rev.A 90 052314)的工作基础之上,提出了一种基于标记单光子源的态制备误差容忍量子密钥分发协议.本文将发送端制备态误差进行参数刻画并带入量子密钥协议安全性分析之中,避免了实际应用中由于态制备装置的不理想可能引入的安全性漏洞,提高了系统的安全性.同时,为了方便起见,本文采用三强度诱骗态方案开展建模分析与数值仿真计算.仿真结果显示,本文提出的协议对态制备误差具有很好的鲁棒性.同时,由于标记单光子源具有真空脉冲概率低的优点,与此前基于弱相干态脉冲的同类协议相比,我们的协议在传输距离较远时能够显示出更优的性能.因而,该工作有望为未来发展长距离量子保密通信应用与研究提供重要的参考价值.

1 引言

量子密钥分发(quantum key distribution,QKD)协议主要利用量子态编码信息来实现密钥安全分发的目的,其安全性基于量子力学基本原理,理论上具有无条件安全性[1-5].在实际应用中,通信的双方通过QKD 结合“一次一密”操作[6],可以实现无条件安全的保密通信,在避开泄漏隐患的同时,也降低了保存密码本的资源与成本,因此受到了广泛关注.在早期的QKD 协议安全性分析过程中,如原始的GLLP 协议[7],没有考虑态制备误差,一般假定量子态的制备过程是理想的.而在实际实验条件下,由于设备存在缺陷,比如相位调制器、偏振调制器等器件存在调制误差,导致态制备存在误差,降低了系统的现实安全性.随着研究的深入,将态制备误差考虑进量子密钥协议安全性分析过程中的思想引起研究者的关注.2014 年,Tamaki等[8]在GLLP 协议[7]的基础上考虑了调制误差在内的源缺陷,提出了一种误差容忍(loss tolerant,LT)QKD 协议.随后徐飞虎等[9]和唐志远等[10]分别在实验上进行了演示验证.在此基础之上,一系列与光源安全性相关的研究工作相继开展[11-15].

不过,以上研究工作使用的大多数是弱相干态光源(weak coherent source,WCS),该光源服从泊松分布,包含相当比例的真空态脉冲.由于真空态脉冲在远距离时会对系统误码率产生重要影响,因而使得基于WCS 的误差容忍协议的最远安全传输距离收到一定限制.针对以上问题,本文提出了基于一种基于标记单光子源(heralded singlephoton source,HSPS)的态制备误差容忍(state preparation error tolerant,SPT)量子密钥分发协议,并且以三强度诱骗态方案[16,17](信号态+弱诱骗态+真空态)为例进行相应的模型分析与数值仿真计算.

2 HSPS 与WCS 光源比较

标记单光子源一般由参量下转换(PDC)过程产生,其产生示意图如图1 所示.泵浦激光作用在非线性晶体上,经PDC 过程产生分布一致的双模压缩光场,即参量光,其中一路通常称为信号光(signal),另一路称为休闲光(idler)[18-22].选择合适的实验条件,可以使参量光服从热分布或是泊松分布[23,24].本文以具有泊松分布的参量光为例来进行介绍.

图1 实际系统中的标记单光子源的光路装置模型Fig.1.Model of optical path device for marking single photon source in experimental system.

如图1 所示,参量光经二向色镜(DM)分开后,其中休闲光经本地探测器(D1)探测后,产生同步电信号,可以对信号光起到标记作用.被标记后的信号光被称为标记单光子源(HSPS),在光子数空间可表示为:,其中l为每脉冲包含的平均光子数;为在l平均光子数强度下包含i光子态的概率.假如本地探测器的探测效率和暗计数率分别记为ηA和dA,则被标记后的光子数分布可表示为:.在QKD 过程中,发送方Alice 在本地制备HSPS,然后通过量子信道发送给接收方Bob,Bob 使用探测器D2 进行探测,探测器效率为ηB.

表1 比较了在平均光子数强度为0.4 时,HSPS与WCS 两种光源中不同光子数脉冲在总脉冲数中所占概率(此处假设ηA=0.75 ,dA=10-6)[23-25].由表1 可见,WCS 中包含大量的正空脉冲的比例,而HSPS 中包含真空态脉冲的概率几乎可以忽略不计.

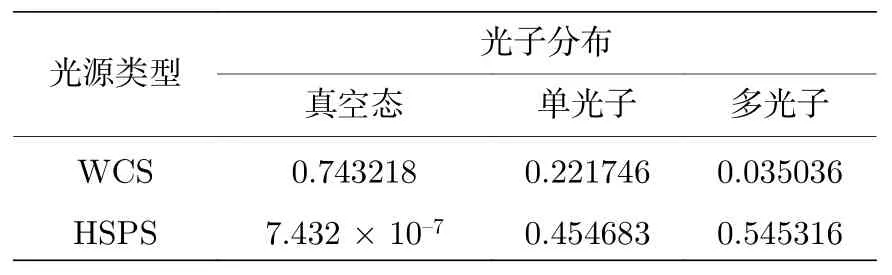
表1 在平均光子数强度为0.4 时,WCS 和HSPS光源中不同光子数脉冲出现的概率Table 1. Proportion of different photon number pulses in WCS and HSPS when the average photon intensity is 0.4.

3 理论模型

在实际的QKD 系统中,由于器件的不完美,不可避免地存在量子态制备误差,若不对此种情况加以考虑,窃听者Eve 可能会利用这一安全性漏洞进行攻击,窃取信息从而导致系统性能的下降.针对这一问题,我们提出了基于标记单光子源的态制备误差容忍量子密钥分发协议,该协议通过将态制备误差加以刻画,将其纳入考虑范围,使得窃听者不能利用这一缺陷窃取信息,理论上减小了系统对量子态制备过程的漏洞,使得该模型的结果可以对误差具有一定程度的容忍性能,模型的鲁棒性得以增强.并且研究了该协议在不同态制备误差条件下的性能.

3.1 计算相位误码率eX

首先,Alice 利用相位调制器随机制备三种量子态{|φ0Z〉,|φ1Z〉,|φ0X〉}.由于现实环境下相位编码或偏振编码等系统在态制备过程存在一定的缺陷,制备出的量子态本身不可避免地会与预期存在一定偏差,通过借鉴文献[8]中的定义,对量子态中的误差刻画如下:

其中δ(δ≥0)表示相位调制器(PM)或偏振调制器(PR)与预期结果相比的调制偏差,也称为态制备误差[8].

我们所选用的标记单光子源采用了光子对纠缠的方法,在纠缠的光子对中假定一个光子到达的时间可以由另外一个光子表示.由于纠缠的光子具有同时性,通过被指示的那个光子到达时间标记,可以较为准确地控制探测器的开关时间以降低真空脉冲和多光子脉冲的概率值,从而提高单光子脉冲的概率,有效地减少长距离量子密钥分发过程中暗计数的影响,进而增加系统的安全传输距离[23,24,26].

基于纠缠协议,Alice 发送量子态等价于制备量子态,具体表示如下:

其中A 表示Alice 方所拥有的系统,Ae表示Alice拥有的扩展系统,B 表示发送给Bob 方的系统,Alice 经过选基测量系统A 后发送系统B 给Bob方.(2)式表述的是Alice 针对发送量子态的态制备过程,是态制备的等价纠缠态.通过(2)式可以看出,Alice 在选择X基时只制备对应于比特0 的量子态,选择Z基时制备对应于比特0 与比特1的量子态,制备的量子态可以通过偏振编码或者相位编码应用于量子密钥分发过程.该态制备过程不依赖于具体光源,同样适用于HSPS 光源.

然后将定义相位误码率表征为X基的虚拟比特误码率,表达式如下表示:

若要求虚拟协议下的比特误码率,首先要求出虚拟协议下的传输速率.研究表明,虚拟态传输速率由虚拟态发送的概率与虚拟态在对应基下成功测量的概率两者构成,具体表示如下:

考虑到真实态也位于X-Z平面,由实验数据,可以得出实际传输速率表达式为.经过变量代换,可以表示如下:

其中参数P(jα)表示Alice 方实际发射态的概率,分母表示Bob 选基的概率,表示σt的传输速率.进而可得出实际传输速率的表示形式:

本文通过建立等价虚拟协议,不仅可以针对目标参数—相位误码率eX进行了准确表征,而且在真实的QKD 协议框架中,测得实际传输速率结果后,通过分别探寻实际传输速率、虚拟态传输速率与信道参数的数学关系,以信道参数为媒介可以反向求出虚拟态传输速率,最后代入相位误码的表达式得出结果大小.

3.2 单光子脉冲增益 Q1 与系统增益Qμ

为了计算最终安全密钥生成率,需要对单光子的穿透率(Y1)下界和单光子的误码率(e1)上界进行估计.理想情况下,Alice 发送n光子,接收方探测器响应的概率Yn为

其中Csα|jγ表示接收端选择α作为测量基时对|φjγ〉态进行测量并获得强度S的理想概率.h代表光子从Alice 端到Bob 端的传输效率,其表达式可写为:η=ηB·10-αl/10,其中α为信道的衰减系数,l为信道的长度.光子态增益由光源分布以及探测器响应概率Yn组成,由于增益受到HSPS 光源亚泊松分布的影响,其表达式所示如下:

将增益的求和定义式进行展开,进行不同的放缩移项,分别利用信号态增益、单光子增益与单光子响应率的关系,可以得到使用HSPS 光源时单光子脉冲响应率的上下界、单光子的增益(Q1)以及系统总增益(Qμ),具体表示如下:

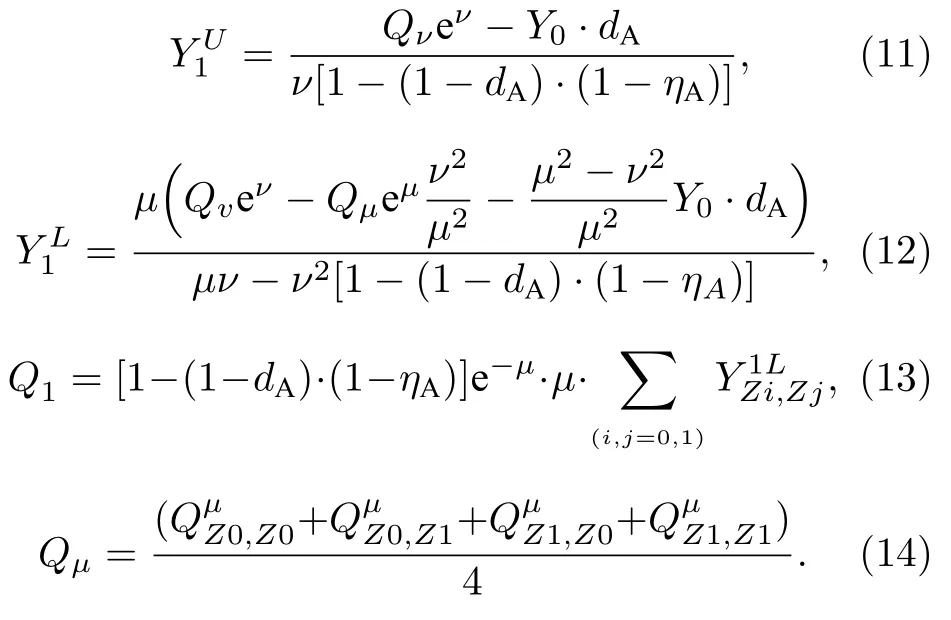
3.3 密钥生成率R

系统量子比特误码率Eμ定义为

将以上参数代入下面密钥率公式,即可计算密钥率大小:

其中,f为系统纠错系数;eX为相位误码率;Eμ为系统量子比特误码率;h(x)为香农熵函数:h(x)=-xlog2(x)-(1-x)log2(1-x);通过求解前面参数,可以算出最终的安全密钥[9,17].

4 数值仿真结果及分析讨论

在数值仿真中,使用合理的实验系统参数[23-25],如表2 所列.

表2 基于HSPS 的三强度诱骗态态制备误差容忍QKD 协议仿真使用的参数列表Table 2. Parameter list used in simulation of state-preparation-error tolerant QKD protocol for three strength decoy states based on HSPS.

为了说明本协议与基于WCS 光源的误差容忍协议的区别,分别画出了态制备误差为0 和0.4时两者的密钥率随距离的变化曲线,如图2 所示.

图2 基于不同光源的态制备误差容忍协议密钥生成率对比图Fig.2.Comparison of the key generation rates of the two different state-preparation-error tolerant protocols using either HSPS or WCS.

由图2 可看出,在相同的态制备误差的情况下,当近距离时(＜150 km),基于WCS 光源的协议显示出高于基于HSPS 协议的密钥生成率,主要由于在后者方案中所使用的本地探测器的探测效率较低所致.不过在远距离时(＞200 km),基于WCS 光源方案的密钥生成率急剧下降,而基于HSPS 光源方案的密钥生成率下降趋势相对平缓.比如,前者在211 km 后已经不再能生成密钥,而后者最大传输距离可达到228 km.以上结果说明了本协议更适合应用于远距离量子密钥分发应用.

下面考察使用相同的光源(HSPS),但是不同的态制备误差下(δ=0,0.2,0.4,0.6),使用本文提出的协议与使用GLLP 协议[24]的密钥生成率有何区别,如图3 所示.

图3 中的两种协议使用的仿真参数与表2 相同,其中虚线代表本协议在不同的态制备误差条件下密钥生成率随距离变化的曲线,从上到下四条虚线分别对应态制备误差为δ=0,0.2,0.4,0.6 时的结果;四条实线分别代表使用GLLP 协议的对应结果.由图3 可看出,在态制备误差为零时,后者(使用GLLP 协议)的码率更高;但是随着态制备误差的增大,后者的码率急剧下降.而本协议随着态制备误差的增大,密钥生成率变化非常缓慢,尤其是在态制备误差相对较小时,比如δ=0.2 时密钥率曲线几乎与δ=0 时密钥率曲线重合.以上结果证明了本协议对态制备误差具有极好的鲁棒性.

图3 在不同态制备误差下,对比本协议与GLLP 协议[24]的密钥生成率随传输距离变化趋势Fig.3.Comparison of the key generation rate between the present work and GLLP protocol under different state preparation errors.

5 结论

本文提出了基于HSPS 的态制备误差容忍量子密钥分发协议,随后以三强度诱骗态方法为例来进行模型构建和参数估计方法介绍,同时开展相应数值仿真计算.该协议对发送端制备态误差大小进行刻画并带入安全性分析之中,避免了可能存在的安全性漏洞,提高了系统的安全性.由于本协议所使用光源自身的优势,与此前基于WCS 光源的同类协议相比,在远距离传输时具有更优的性能.同时,本协议对实际量子密钥分发系统中存在的态制备误差具有良好的鲁棒性,几乎不影响其密钥产生率大小.

本方法原则上同样可以与测量设备无关的量子密钥分发协议[27-30]以及双场量子密钥分发[31-34]等协议结合,进一步增大系统所能支持的安全通信传输距离.因而,该工作为未来发展长距离量子保密通信实际应用起到重要促进作用.

感谢南京邮电大学通信与信息工程学院张春辉老师和周星宇老师的帮助与讨论.