基于置换群的多粒子环上量子行走的反馈搜索算法*

姜瑶瑶 张文彬 初鹏程 马鸿洋†

1)(青岛理工大学理学院,青岛 266033)

2)(青岛理工大学信息与控制工程学院,青岛 266033)

在量子计算科学中,如何更好地构建量子搜索算法一直以来受到学者们的广泛关注,并且基于量子行走寻找新的搜索算法也仍吸引着学者们不断深入研究与探索.本文从减少搜索过程中的时间消耗、增加算法搜索的准确性和可控性等多方面进行考虑,提出了一种基于置换群的多粒子量子行走搜索算法.首先分析得到置换群在空间中可看成一个闭环,定义了置换集合,并且通过同构映射将数据点所在数据集映射到定义的置换集,使得置换集合中元素数据点形成一一对应的关系.其次,根据给定初始态和硬币算符,在数据点集与置换集合张成的搜索空间中利用多粒子的量子行走在环上进行目标数据搜索.最后,根据函数 Φ(w)=1 找到目标数据,并用量子态存储数值,用于形成搜索算法的反馈控制;同时通过控制硬币算符从而控制量子行走在环上的行走方向,增加搜索的可操作性与准确性.本文利用多粒子的量子行走进行搜索,分析得到粒子数量参数j 与时间复杂度呈非线性负相关;提出的量子行走搜索算法符合零点条件与下确界条件,且不受变量数j 的影响;通过数值分析得到量子行走搜索算法的时间复杂度等价于,相比于Grover 搜索算法提高了搜索效率.

1 引言

量子行走作为经典行走的推广,是量子计算的基础,被视为实现量子计算的一种主要工具.量子行走利用量子态的叠加性,能够实现同时行走在不同线路上的可能性,因此与经典行走相比,量子行走的效率有着指数级的增长.并且行走者位置的概率分布也与经典行走有着截然不同的形式,这些性质都有利于量子算法的实现.量子行走最初是由Aharonov 等[1]及Farhi 和Gutmann[2]提出的.其中Aharonov 等[1]提出了离散时间状态下的量子行走算法;Farhi 和Gutmann[2]提出了连续时间状态下的量子行走算法.与经典行走相比,这两种行走方法都提供了加速效果.Godsil 等[3]和Bose[4]展示了如何将图论的思想应用到量子行走中来实现更好的状态传输;Childs[5]证明了量子行走可以实现普适的量子计算.这些成果都体现了量子行走在实际应用中的重要性.此外,基于量子行走的许多搜索算法都体现了量子行走在算法领域具有独特的优势[6-12].

在搜索算法中,Grover 算法是第二个量子革命的一个里程碑[13].除了数据库搜索,它还可以用于求解特征值问题,这是目前最热门的课题之一.2010 年Childs[14]提出基于连续时间量子漫步的算法,在黑箱问题中量子行走成功实现了指数级的加速.Shenvi 等[15]也在超立方体的拓扑知识的基础上提出了基于离散时间量子漫步的搜索算法,实现了多项式加速效果.由于搜索算法以及可转化为搜索问题的算法具有广泛适用性的特点,在这些开创性的工作之后,学者们又进行了深入的研究[14,16-23].在国内,Long 等[24-26]不断完善优化Grover 搜索算法,他们研究的算法是所有优化的Grover 算法中最优的,又称龙算法[26];Zhou 等[27-30]和Sheng等[31,32]也分别在量子搜索算法和量子计算领域做出了贡献.考虑到量子计算的优势,学者们期待大量新的量子算法的出现,但事实证明这项任务很难,值得继续研究和探索.

基于量子行走寻找新的算法仍然是持续努力的方向,本文提出了一种基于置换群的空间量子行走搜索算法,将置换群作为搜素算法和量子行走相结合的桥梁,目的是减少搜索时间,提高目标搜索的精度,提高空间内的搜索效果.根据置换群中的元素在几何中可以形成环的性质,将量子行走应用到置换群中,从而实现在置换群中的量子搜索.首先通过设置同构映射,将数据点集合映射到由多个置换群组成的置换集合中的元素,为了能够实现环上的量子行走,在同构映射的作用下使数据点集合和置换集合具有一对一的对应关系.然后,构造Hilbert 空间,通过控制硬币算子,给定初始状态,将搜索空间中的元素作为节点,进行量子行走.接着根据函数Φ(w)=1 得到目标点,并用量子态存储函数值.最后根据函数的数值形成算法的反馈控制,以此来判断量子行走的方向以及确定行走的状态.本文有3 个创新点:1)将数据集同构到置换集,实现了置换群上的量子行走;2)多粒子受控的量子行走;3)增加了反馈控制,增强算法的可操作性与可控性.

本文结构如下:第2 节简要介绍置换群S3以及环上的量子行走;第3 节分析并实现量子行走搜索算法,其中包括10 个步骤;第4 节对量子行走搜索算法进行时间复杂度分析;第5 节根据时间复杂度进行数值仿真,直观明了地体现数值结果;第6 节对算法进行总结.

2 相关工作

2.1 置换群S3

定义2.1 (置换群):有限集合到自身的一一映射称为一个置换.有限集合S上的一些置换组成的集合,在置换的乘法下所组成的群,称为置换群[33].任何一个有限群都同构于一个置换群.因此,可以把一切有限群都看成置换群.任一置换可表示成若干不相交循环的乘积,如(a1,a2,···,an)=称为置换的循环表示.由于每个循环首尾相连,因此可以看成是一个闭环.

本文置换群的选择是根据搜索空间中目标态的维数决定的.由于本文提出的搜索算法是在三维空间中进行的,因此只对置换群S3进行研究,若搜索空间是n维,可以换成置换群Sn,置换群的选择并不会影响算法的时间复杂度.其中

S3={(e),(ab),(ac),(bc),(abc),(acb)}.

2.2 环上行走

假设群G是有限群,S是该群的生成集合,环A和群G存在一一对应关系,若节点g和g′满足g′=gh,则存在一条边 (g,g′),其中g∈G,h∈S.将环A中元素量子化:

其中,HS为硬币算符所在的Hilbert 空间,HG为量子行走所处的位置空间.环上量子行走的演化算符为U=T(C⊗I),I为位置空间的单位算符,C为硬币算符,T为转移算符,具体定义如下:

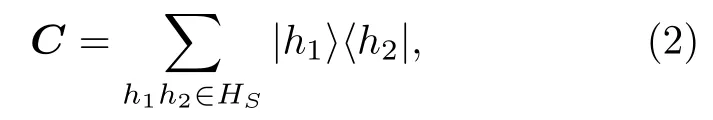
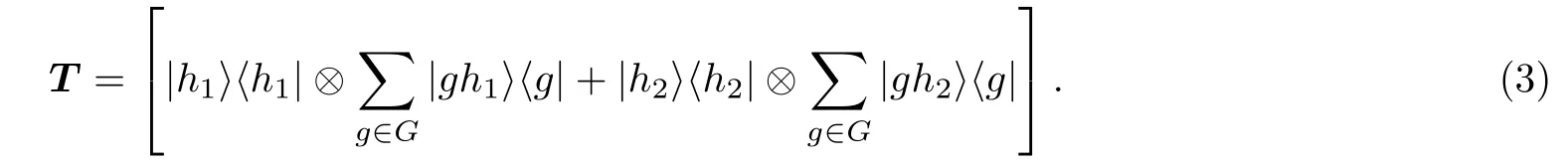
3 量子行走搜索算法

3.1 初始化阶段

步骤1应用置换群的对称运算

在介绍量子行走搜索算法之前首先利用对称运算证明置换群S3的每个子群在空间中形成一个闭环,并且根据旋转角度,规定群内元素的次序.为了便于下文解释说明,将群中元素a,b,c替换为1,2,3.

对于置换群S3,有如下保持三角形不变的对称运算:(e)是一个恒等变化;(123),(132)分别为绕中心点逆时针旋转;(12),(13),(23)分别为围绕x,y,z轴逆时针旋转π.每个元素旋转情况如图1 所示.同时可以得到置换群S3的4 个子群:

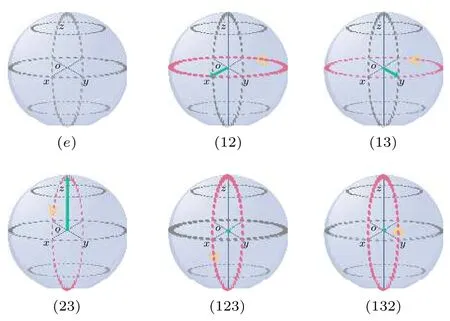
图1 置换群 S3 中每个元素的旋转方位图Fig.1.Diagram of the rotation position of each element in the permutation group S3.

H1={e,(12)},H2={e,(13)},

H3={e,(123),(132)},H4={e,(23)}.

按照元素的旋转角度,以单位元为起点,规定每个子群的元素排列顺序.例如在子群H1中,第一个元素是e,第二个元素是 (12).同理可得其他子群元素之间的排列顺序.置换群S3的每个子群内,各元素在三维空间中的旋转关系如图2 所示.在图2中,对于子群H1,元素e绕X轴逆时针旋转π 到达 (12)的位置,同样地,元素 (12)绕X轴逆时针旋转π 到达e的位置;同理可得其他子群元素之间位置的旋转关系.从图2 还可看出,置换群S3中每个子群元素之间通过置换群特有的对称运算,形成了一个闭环.

图2 在每个子群中各个元素之间的旋转关系图Fig.2.Diagram of the rotation relationship between the elements in each subgroup.

3.2 构造行走搜索空间

本节将数据点集与置换群元素通过同构映射实现一一对应,从而构建量子行走的搜索空间.

步骤2构建置换群元素新集合

定义3.1 (数据集):由数据点d1,d2,···,dN生成的集合称为数据集D,其中n表示量子态数量,N=2n.

定义3.2 (置换集):集合P{p(i,j,k)},i,j,k∈Z是由元素p(i,j,k)生成的,称为置换集.其中元素p(i,j,k)通过旋转一定角度变成元素p(i,j,k+1),并且集合P中的元素数量大于等于数据集D中的元素数量.

构建置换集的具体过程:由置换群的子群Hi衍生出子群族.对于固定的i,j,子群由p(i,j,k)元素生成.其中i=1,2,3,j∈Z.对于子群,j表示第j个子群Hi,k∈Z表示子群第k个元素.对于同一个i的值,只要j1/=j2,则.同理,只要k1/=k2,则p(i,j,k1)/=p(i,j,k2).

对于集合P和每个子群,即使包含的元素数与元素的性质相同,我们也规定,只要j是不同的,就被认为是不同的子群.此外,对于同一个元素(如e),只要子群不同,就被认为是不同的元素.并且每个子群的元素顺序是逆时针方向.如对于子群,指定第一个元素为e,第二个元素为(12).对于的子群,元素e标记为p(1,j,1),(12)标记为p(1,j,2).集合P=p(i,j,k)中的每个元素都可以唯一地表示.元素在置换集中的分布如表1 所列.

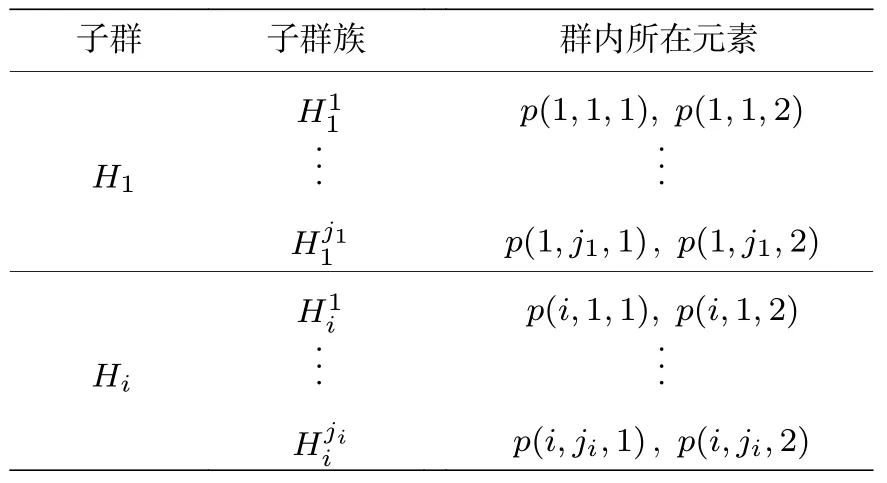
表1 置换集合元素分布情况Table 1. Distribution of the elements in permutation set.

又因为

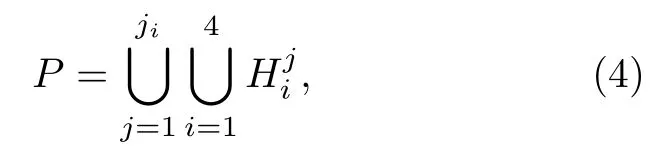
因此得到置换集中的元素数满足N==2n,其中ji表示Hi的子群数,ki表示元素数.

步骤3建立置换集与数据集同构

假设映射F

pm(i,j,k)上标中的m无意义,只是为了方便区分说明,其中m=1,2,···,N.接下来证明,映射F是同构的.

证明令F(da)=pa(i,j,c),F(db)=pb(i,j,d).由于pm(i,j,d)的位置只对应于数据点dm,因此当a/=b时,p(i,j,c)/=p(i,j,d)⇒da/=db.证得F是单射.

又因为da/=db(a/=b),由元素的唯一性得到p(i,j,c)/=p(i,j,d),所以映射F是同构映射.

步骤4建立量子行走搜索空间

定义3.3 (搜索空间):空间W是W=D×P集合生成,其元素定义为w(dm,pm(i,j,k))∈W,被称为搜索空间W.每个元素w(dm,pm(i,j,k))包含排列集中的数据点dm和相应的位置pm(i,j,k).

重新构造搜索函数Φ(w)=Φ(d)={0,1}.由于pm(i,j,k)只充当w(dm,pm(i,j,k))中的位置坐标,该函数对pm(i,j,k)不作用.这样,通过函数Φ(w)=1得到wtar(dtar,ptar(i,j,k)),从而得到目标数据dtar.

定义3.4 (集合W-1):搜索空间W中定义了一个集合W-1={w-1(-1,p(i,j,k))}.该集合与W的集合相比,在相同位置p(i,j,k)上,集合W-1中的数据d=1.集合W与W-1的元素对应关系如图3 所示.

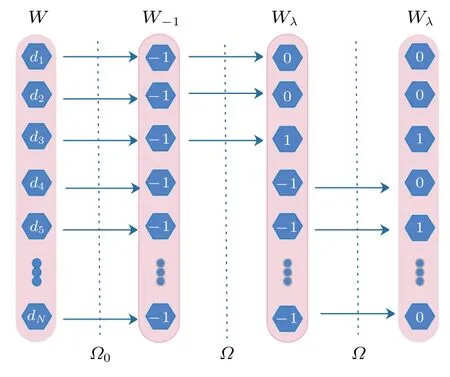
图3 集合W,W-1 和 Wλ 元素之间的对应关系Fig.3.Corresponding relationship between elements of the sets W,W-1 and Wλ .

集合W中的元素和集合W-1中的元素满足下列关系:

其中Ω0是转化函数;φ0是矩阵并满足

3.3 确定行走粒子数量

步骤5确定量子行走粒子数量

根据置换集合对应的子集数目,确定量子行走过程中粒子的数量.再根据前面的假设,得到子集数j1+j2+j3+j4.为了方便计算,选择j1+j2+j3+j4的最大值 4×max{j1,j2,j3,j4}.在不失一般性的情况下,令j=max{j1,j2,j3,j4}.得到j1+j2+j3+j4≤4×max{j1,j2,j3,j4}=4×j.

因此,得到子集的数目是 4×j,即量子行走过程中粒子的数目是 4×j,其中 0≤j≤N/4.

3.4 行走过程

前文得出置换群S3的每个子群在空间中形成一个闭环,并且置换群也与Zn的加法群同构.根据已经提出的基于Cayley 图的量子行走算法[34],可以得到置换群S3上的量子行走.

步骤6置换群上量子行走

将置换群看成是闭环,则它的数学描述如下:假设G是一个有限群,S是该群的生成集合,置换群S3的元素和群G的元素之间存在一一对应关系.并且如果两个节点g和g′满足g′=gh,其中g ∈G和h∈S,则这两个节点之间存在一条边 (g,gh).将置换群的元素量子化,则置换群上的量子行走可以有如下定义:假设HS是硬币算子所在的Hilbert空间,它是由态|h〉,h∈S生成的;HG是行走者的位置空间,它是由态|g〉,g∈G生成,则演化算符U=T(C⊗I)的硬币算子C和转移算子T分别定义为

其中,转移算子的作用是

从(9)式可以得到,在置换群上进行量子行走时,以g为起点位置,当硬币算符为h1时,行走者会由节点位置g转移到相邻节点gh1,其中gh1=g′.根据相邻节点的关系,可以得到:

其中⊕是模 2加运算或模 3 加运算(在H3中).

对群元素进行傅里叶变换[35],算子的形式如下:

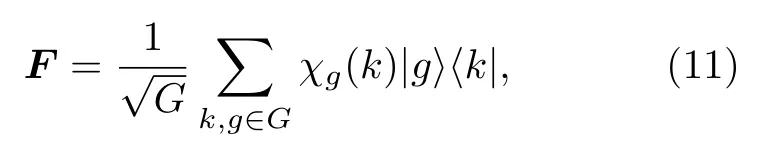
其中,χg为群的特征标,.

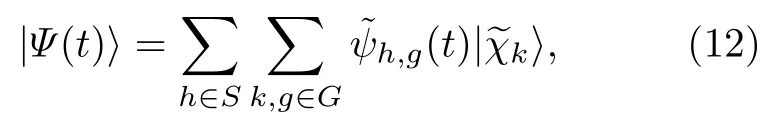
其中,转移算符对傅里叶基态作用后的形式为

可以证明傅里叶基态下,转移算符只改变基态的振幅.

最后,得到傅里叶基态下t时刻的振幅为,通过逆傅里叶变换求解离散时间的振幅:

3.4.1 构造Hilbert 空间

步骤7构造Hilbert 空间并检测合理性

确定硬币算符C,通过硬币算符控制每一步行走.这一步的目标是保证量子行走的方向一致,不会往返.然后通过迭代算子U=T(C⊗I)⊗Θ,进而通过迭代的方法得出迭代算子的数值解.其中当算子Θ作用到元素w(dm,pm(i,j,k))时,可以得到数值δ={1,0}.根据硬币算子C在本文中的作用,其被定义为

其中S={-1,1}.并且令:

根据构建的Hilbert 空间,检验转移算子T、转换算子Θ和迭代算子Ui是酉算子,其中i=1,2,3.推导结果如下:

因为转换算子

得到

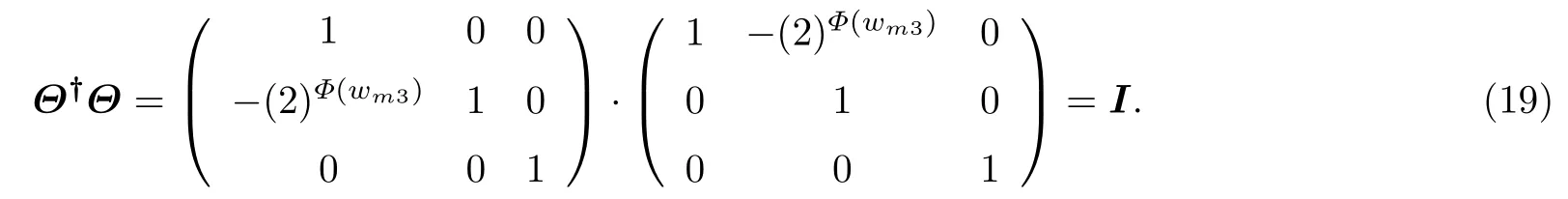
又因为

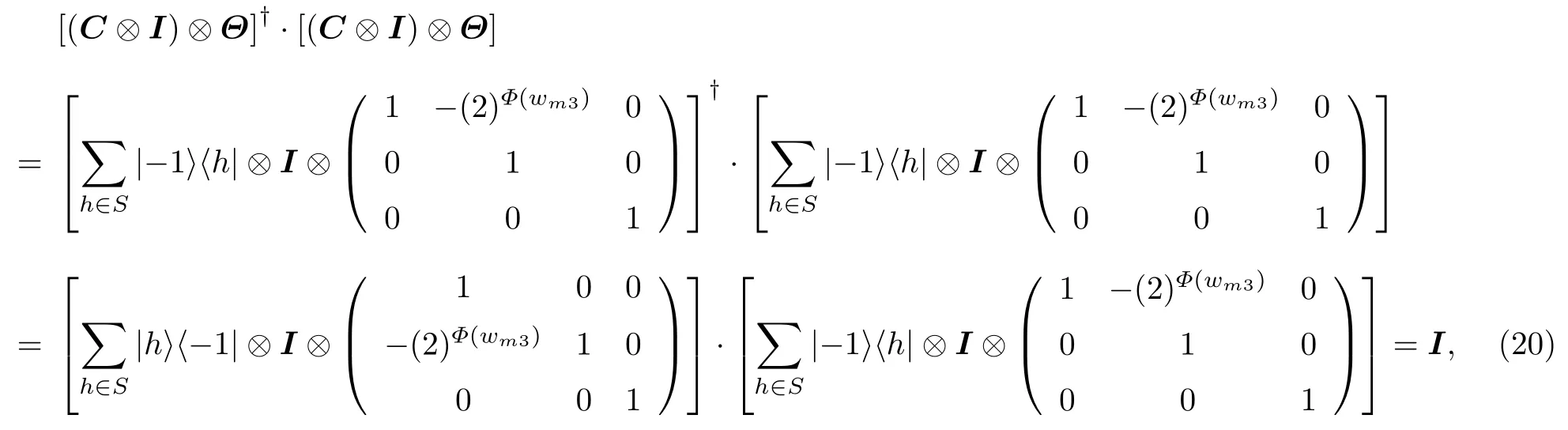
根据U=T(C⊗I)⊗Θ,得到:

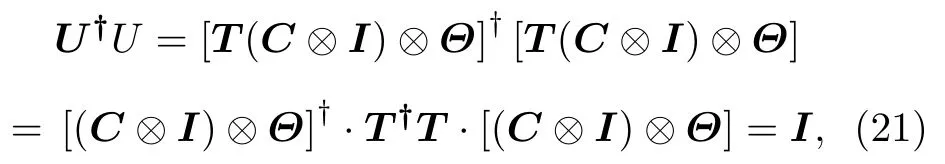
因此通过上述验证过程得出转移算子T、转换算子Θ和迭代算子Ui是酉算子.

3.4.2 执行行走过程

步骤8分析量子行走路径

Ui=ψt=1=|-1〉⊗|-i〉⊗|δ〉,

从而控制了在置换群中的量子行走方向.整个量子行走过程如图4 所示.

图4 量子行走的过程Fig.4.Process of quantum walk.

图4 中黄色的圆点表示数据点,绿色的球体表示空间,标有数字 1,2,3 的蓝色圆圈表示数据点pm(i,j,1),pm+1(i,j,2),pm+2(i,j,3),位置在某个子群中.红色的虚线表示运动轨迹,从1→2→3都是利用反馈控制继续前进的.当 3→1 时,运动轨迹就是黑色箭头所表示的方向,通过反馈控制,发现此方向是被禁止的,于是设定硬币算符为,随机选择行走方向(橙色箭头),进行下一个子群中进行的量子行走.

3.5 储存数值结果

步骤9存储函数结果形成反馈控制

当Φ作用于元素w(dm,pm(i,j,k))时,得到函数的值δ=1或 0,并将数值存储在量子态中.其中对于量子态|1〉,表示所对应的数据d正是目标数据dtar.为了形成含有数值结果的量子态集合,让δ替换W-1集合中的-1.

更换过程如下:

其中,Ωi(Θi)表示转换函数,使得数据d=-1(d)成为δ,表示Hi中的一个元素,表示wmi在函数Φ的作用下的函数值,i=1,2,3,4.φi是矩阵并满足

φi是矩阵并满足

当函数Ωi(图3 中简称为Ω)在进行数据更新时,存储函数值的量子态会出现3 个数值,分别是|1〉,|0〉和|-1〉.为了方便说明,用量子态|λ〉表示,并且建立集合Wλ={(λ,p(i,j,k))}(W-1→Wλ),其中λ=0,1,-1.集合W,W-1和Wλ三者之间的关系变化如图3 所示.

3.6 反馈结果判定方向

步骤10根据反馈结果判定后续方向

当量子行走进行到某步时,设此时的迭代次数是t.当迭代次数是t+1 时,判断量子行走过程是否继续或者停止.判断过程如下:

当行走到位置pm(i,j,k)时,判断相应集合Wλ对应的数据λ,如果λ＜0,量子行走在此环(置换群)中继续进行;如果λ≥0,量子行走将在此置换群中停止,设定硬币算符为,随机行走到其他置换群的位置.

4 复杂度分析

本文采取多粒子的量子行走,这样时间复杂度取决于数据点的数量N和量子行走的数量j,即时间复杂度t=tin+tout最终取决于参数j和N.

其中,M表示目标点的数量.

分析时间复杂度tin,根据C=∑h|-1〉〈h|,h∈S可以得到每一步的硬币算符是

C1=|-1〉〈1|,C2=|-1〉〈-1|,C3=|-1〉〈-1|,

其中,两个正交向量|1〉和|-1〉可以用来表示硬币的状态.|1〉表示顺时针方向,|-1〉表示逆时针方向.

通过迭代方法,可以得到:

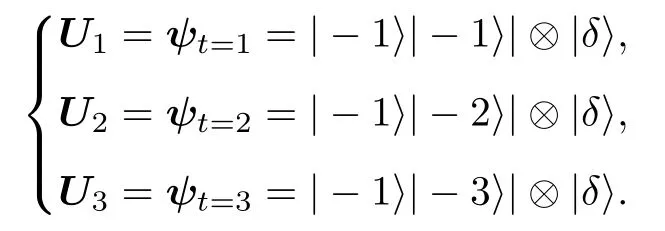
由于本文选择的是置换群S3,因此完成一次置换群上行走次数为t≤3.又因为在在置换群中完成一次量子行走时,才进行一次硬币算符为C*的量子行走.即完成一次更换需要的时间t=tin+tout≤3+1=4,因此完成所有行走过程时间复杂度为t=tin+tout≤4tout,得到t=4tout.所以只需要计算时间复杂度tout即可.

令

于是得到

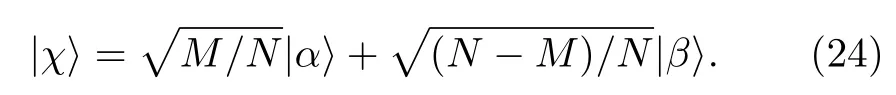
令迭代算符U=T(C*⊗I)⊗Θ作用到量子态|χ〉,通过计算离散量子行走时刻连续叠加态的振幅得到时间复杂度tout和参数N的关系.

其中,当tout为偶数时:

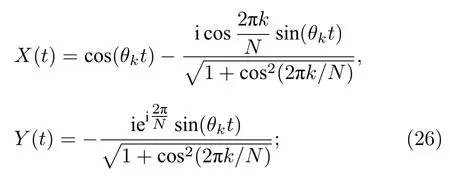
当tout为奇数时:

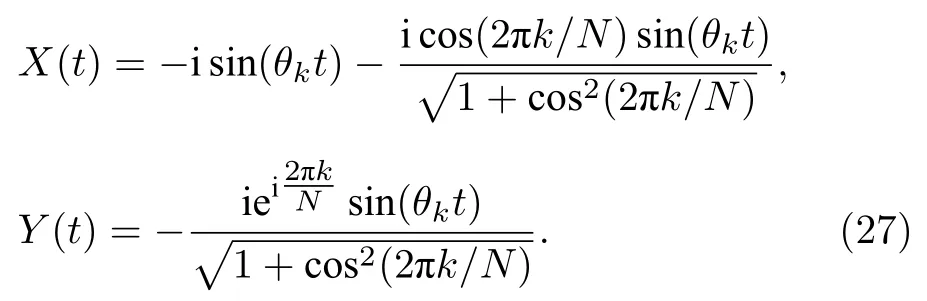
θk满足.

搜索目的是为了找遍空间中所有子群,即搜索到目标数据点的概率等于M/N.

得到:

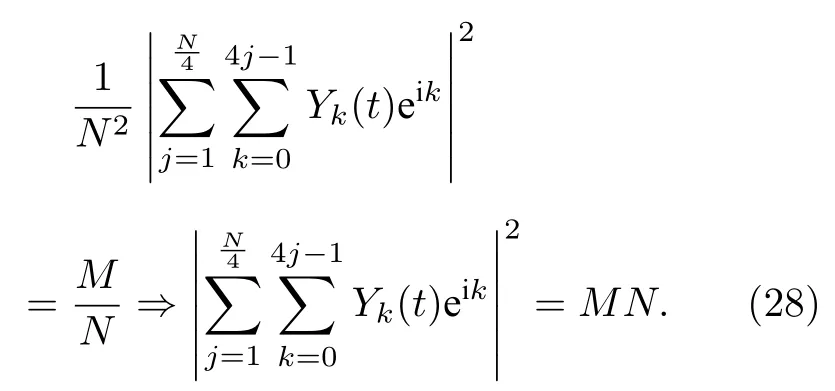
由于参数j与N有关,若取.求解方程(28)可得

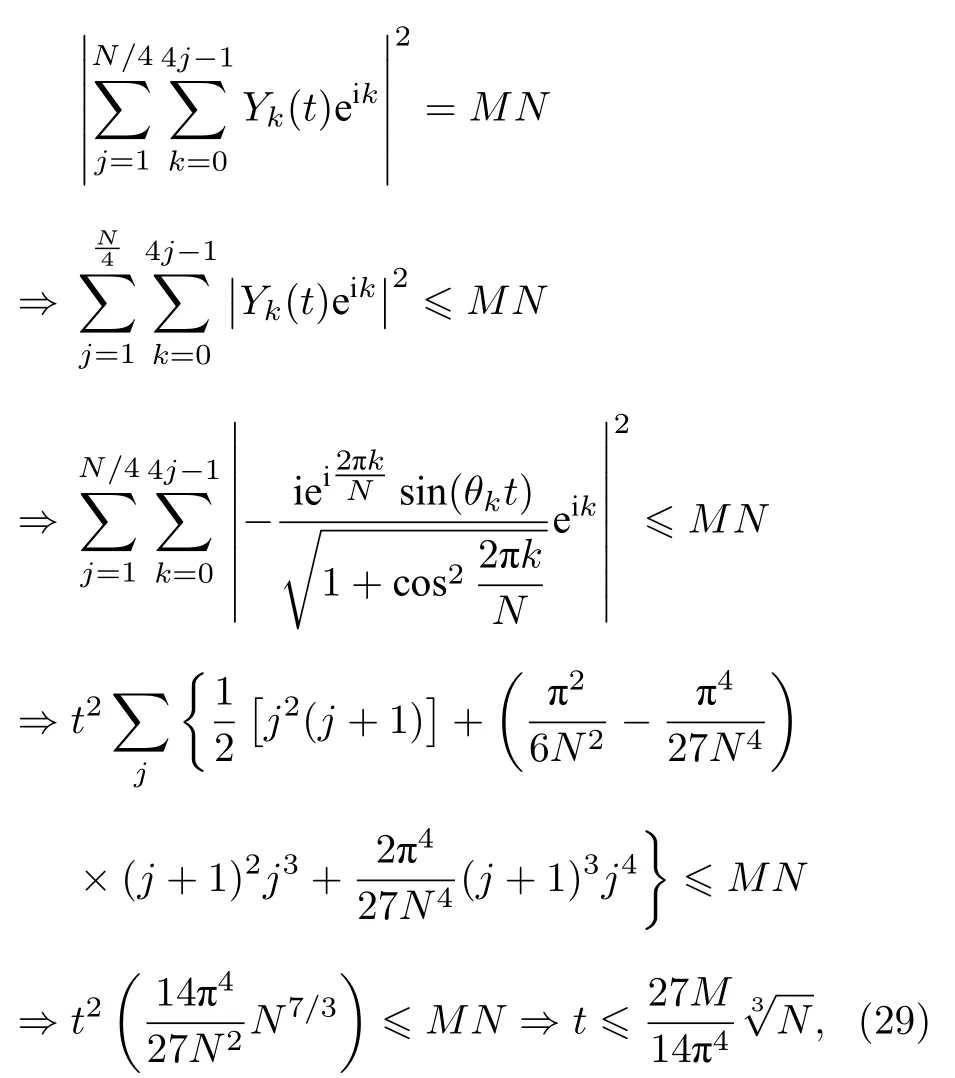
得出关于变量N的数值表达式tout(N)=,即得到关于变量N的数值表达式t(N)=.

5 数值仿真

将本文提出的量子行走搜索算法与Grover 搜索算法关于时间复杂度进行对比,设定参数M=10,N=200,得到图5 所示的对比曲线.从图5(a)得到量子行走搜索算法所用时间要比Grover 搜索算法所用时间短,即量子行走搜索算法的速率更高;从图5(b)得到量子行走搜索算法是满足原点条件和下确界条件的,即满足当N=0时,t=0;N=1时,t=1.

图5 两种搜索算法时间按复杂度的对比Fig.5.Comparison of the time complexity of two search algorithms.

为了直观地体现算法的高效性,下面用两种不同算法进行举例比较:一个采用标准的Grover-Long 算法[36],一个采用本文提出的量子行走搜索算法.N=64时,Grover-Long 算法需要=8次搜索,采用本文的方法,最多需要=4次搜索.

进而又对参数j对搜索的时间复杂度的影响进行了分析.选取了参数M=10,N=200 分别对参数j=1,j=2,j=3 三条曲线进行分析,得到图6 所示曲线.从图6(a)得到参数j与时间复杂度呈负相关,即参数j的取值越大,所用时间越短,搜索速率越快;从图6(b)得到参数j不影响量子行走搜索算法,且满足原点条件和下确界条件.

图6 参数j 对搜索算法时间复杂度的影响Fig.6.Influence of parameter j on the time complexity of search algorithm.

最后分析了变量参数j,N与时间复杂度t的关系,得到数值仿真结果如表2 所列.从表中数据进一步得出,参数与时间复杂度不是呈负线性关系.

表2 数据仿真结果Table 2.Numerical simulation results.

6 总结