Y型微通道内气泡非对称破裂行为的数值研究*
潘文韬 文琳 李姗姗† 潘振海
1) (上海应用技术大学香料香精技术与工程学院,上海 201418)
2) (上海交通大学机械与动力工程学院,上海 200240)
基于微通道两相流的微流控技术已得到广泛的应用,精确控制通道中气泡或液滴的尺寸对相关微流控系统的设计起到至关重要的作用.本文基于流体体积法重构Y型微通道内的气泡破裂行为,系统研究了气泡无量纲尺寸(1.2—2.7)、出口流量比(1—4)以及主通道雷诺数(100—600)对气泡破裂行为的影响.发现气泡非对称破裂过程分为3个阶段:延伸阶段、挤压阶段和快速破裂阶段.在气泡初始尺寸较小或出口流量较大的情况下,气泡不破裂,只经历延伸阶段和挤压阶段.进一步针对不同尺寸和出口流量比揭示了气泡的4种破裂模式:隧道-隧道破裂、阻塞-阻塞破裂、隧道-阻塞破裂和不破裂.随着出口流量比的增大,气泡的破裂过程逐渐变为非对称破裂,其破裂模式沿隧道-隧道破裂/阻塞-阻塞破裂、逐渐向隧道-阻塞破裂和不破裂方向转变.在此基础上获得了不同雷诺数和初始气泡尺寸下,气泡破裂的临界流量比以及气泡破裂后子气泡体积比随出口流量比的变化规律并提炼了相应的准则关联式,可为精确调控破裂后子气泡的尺寸提供理论指导.
1 引言
随着微纳米技术的快速发展,以气液/液液两相流为基础的微流控技术由于其高效、节能、安全、可控的优势,被广泛应用于微化学反应器[1−6]和芯片冷却[7−9]等领域.微流控技术通过生成适当尺寸的微气泡/液滴,利用其独特的尺度效应和流体力学特性来实现功能.研究人员通过控制分岔微通道中气泡/液滴的破裂形态来控制其尺寸,而分岔微通道中的两相流动通常伴随着气泡/液滴的形成、运动、变形、破裂、合并等[10−12]高度耦合的复杂非线性动力学行为,因此充分理解分岔微通道内两相流动行为具有重要意义.
近年来,许多学者对分岔微通道内两相流动问题进行了数值与实验研究.侯璟鑫等[13]和Tan等[14]基于Y型微通道结构,研究了微通道不同的入口角度对产生气泡尺寸的影响,发现不同通道结构下,与液体入口通道夹角为锐角时能产生最短气泡.刘赵淼等[15]研究了Y型入口处连续相毛细数和两相流量比对液滴生成的影响,发现毛细数越小生成液滴的尺寸越大;且随着流量比的增大,毛细数的影响减小,液滴的生成速度增大.学者们还研究了微通道中气泡和液滴的破裂行为.王维萌等[16]基于T型通道进行了可视化研究,将液滴在分岔处的破裂行为分为不破裂、隧道破裂、不连续阻塞破裂和永久阻塞破裂4种模式,并获得了液滴初始长度与破裂的临界毛细数之间的经验关联式.Ma等[17]通过实验研究发现,Y型微通道中的液滴破裂行为也遵循相似的破裂模式,并将破裂过程分为挤压阶段、过渡阶段和快速夹断阶段,研究了两相黏度比对各个阶段中液滴最小颈宽与时间的幂律关系的影响,发现幂律指数随两相黏度比的增大而减小.此外还发现液滴随毛细数和尺寸的增大趋向于破裂.已有的研究[18]表明,液滴的破裂机制在于Rayleigh-Plateau不稳定性,破裂与不破裂间的转化曲线依赖于初始的液滴体积与毛细数的大小.
当前针对微通道内气泡/液滴破裂行为的研究主要集中于对称破裂,针对非对称破裂现象的研究相对较少.Samie等[19]基于T型微通道,通过改变分支通道的宽度比,研究了液滴的非对称破裂过程,发现增大分支通道宽度比会使液滴更趋向于非对称破裂.Zheng等[20]通过研究分支通道的宽高比对气泡破裂的影响发现,气泡在相同毛细数下宽高比越大越难破裂.温宇等[21]还在此基础上研究了不同宽高比下,T型微通道内气泡的体积分配规律,发现随着气液流量比和母气泡体积的增大,子气泡体积分配比呈先增大后减小的非线性变化趋势.此外,分支通道的角度对微通道中的破裂行为也有影响.研究表明[22−24],气泡破裂的非对称性随驱动压力的增大而减小,随分岔角度的增大而增大;而分岔角度越大,气泡越不容易破裂.
综上所述,当前针对微通道内气泡非对称破裂行为的研究主要通过改变微通道的几何结构,构建非对称的几何约束条件加以实现.近年来,Lou等[25]基于格子玻尔兹曼方法,通过改变出口流量比,系统研究了二维Y型微通道内气泡的非对称破裂过程,提示合理调控出口流量比可实现对破裂后子气泡体积的精确控制.有鉴于此,本文基于VOF方法对微通道内的气泡破裂过程进行三维重构,揭示不同出口流量比、雷诺数以及初始尺寸下气泡破裂的动力学特征,定量描述了破裂后子气泡体积受以上3个参数的影响规律,旨在深化对微通道内非均匀出口流量引起的气泡非对称破裂行为的理解,为相关微流控系统的设计提供理论依据.
2 数值方法
2.1 物理模型
本文研究Y型微通道中非均匀出口流量引起的气泡非对称破裂行为,一个孤立的气泡沿主通道流向下游分岔处并破裂,产生的子气泡向两分支通道流出.如图1(a)所示,Y型通道横截面的宽和高皆为W=400 µm,主通道长度为30W,两分支通道的长度为14W,夹角为90°.在0时刻,一个气泡从距离主通道入口为6W处开始随流体流向下游.其初始截面直径d为0.88W,长度l0为1.5d—3d.水和空气在标准温度(20 ℃)下的物理性质见表1.
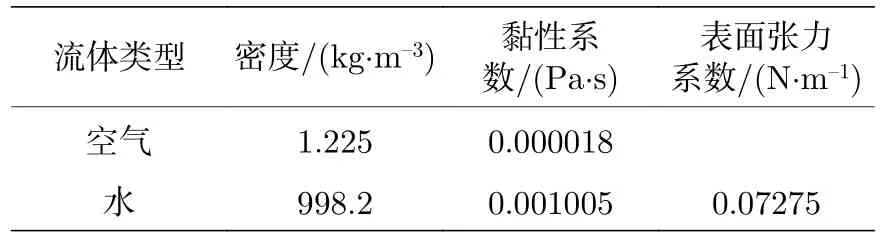
表1 水和空气的物理性质(20 ℃)Table 1.Physical parameters of water and air (20 ℃).
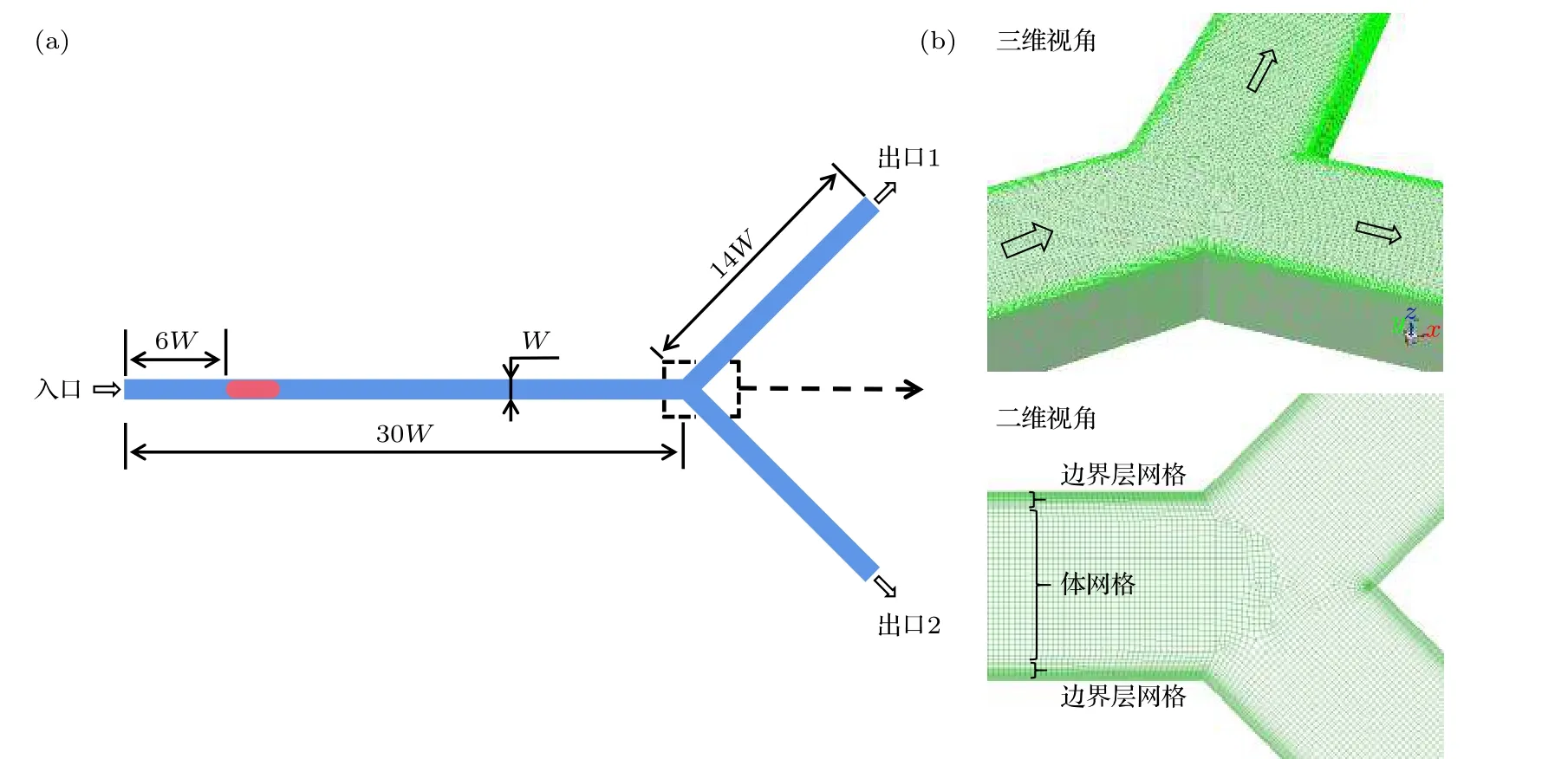
图1 (a) 孤立气泡通过Y型分支微通道的示意图;(b) Y型结区域的网格模型Fig.1.(a) Schematic illustration of an isolated bubble traveling through a Y-shaped branching microchannel;(b) mesh generation in Y-junction region.
本研究采用无量纲时间t∗,定义为

其中U为主通道平均速度.雷诺数Re表示微通道中流体的惯性力与黏性力之比,定义为:
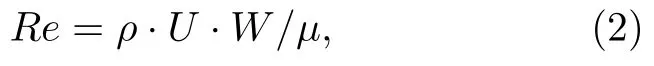
ρ为连续相密度,µ为动力黏度系数.两侧通道的出口流量比定义为:

其中U1和U2分别代表上侧支通道和下侧支通道的平均速度.气泡的初始无量纲体积V∗定义为气泡的初始体积V与以通道宽度为直径的气泡的体积之比:
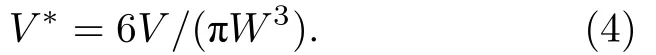
2.2 控制方程
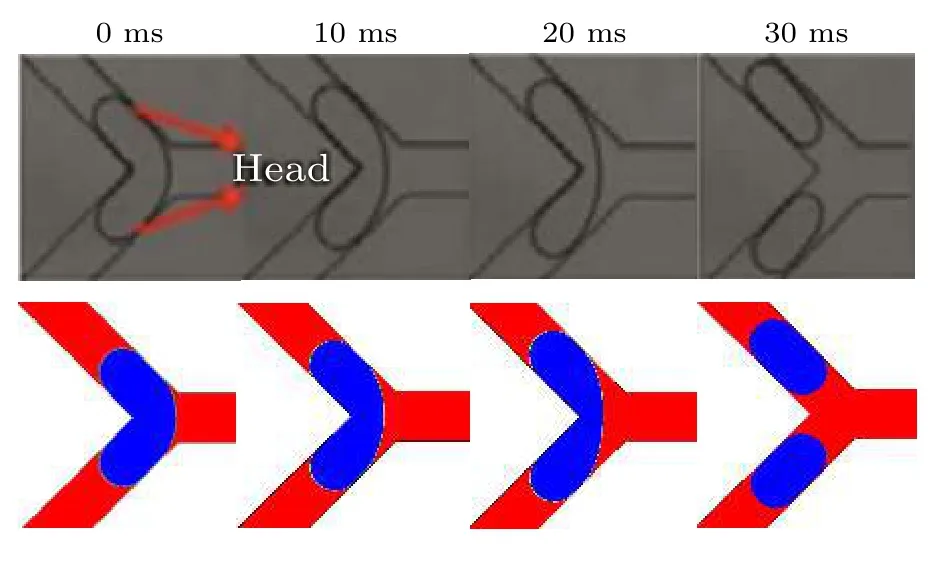
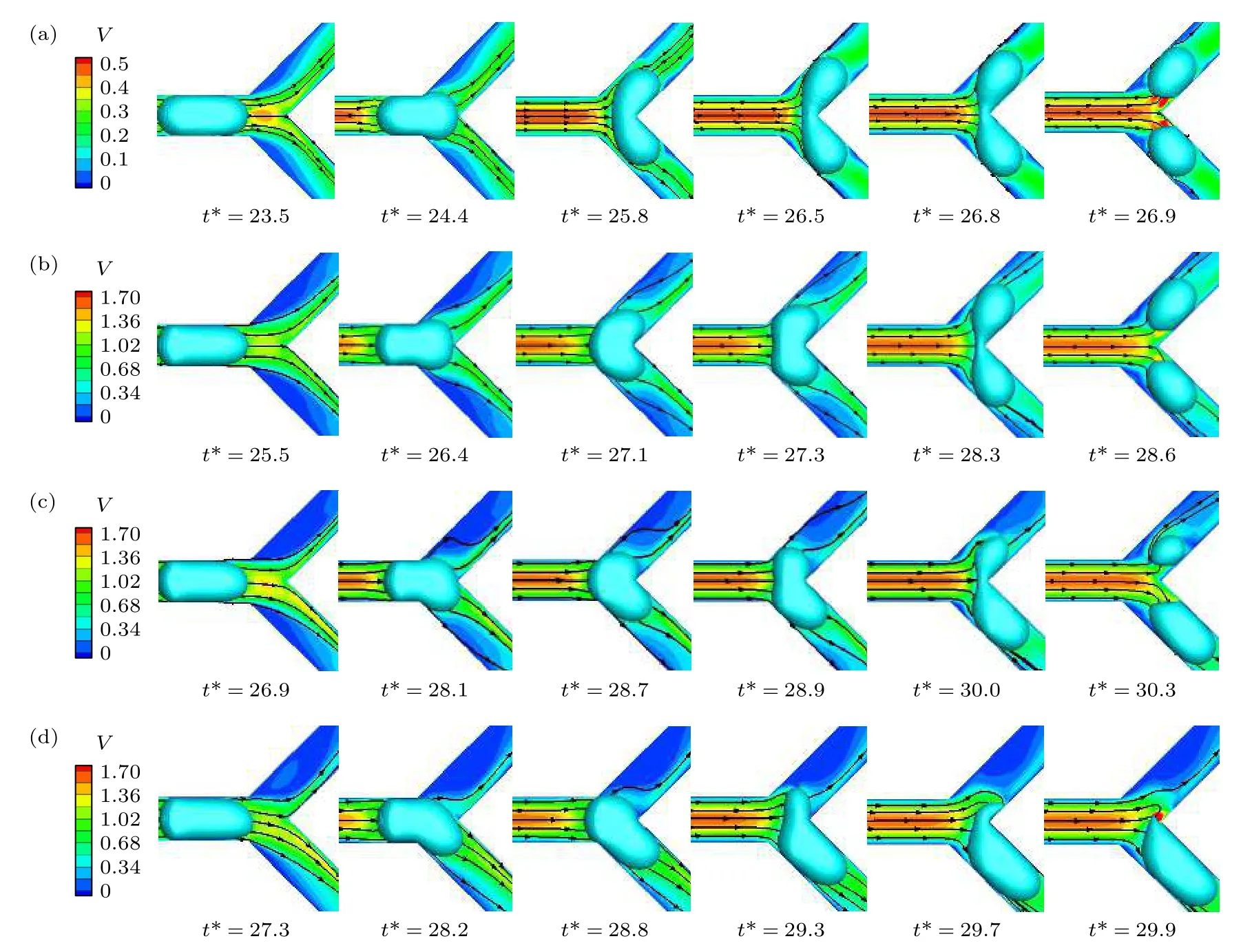
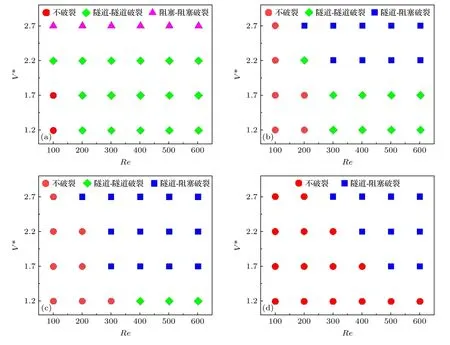
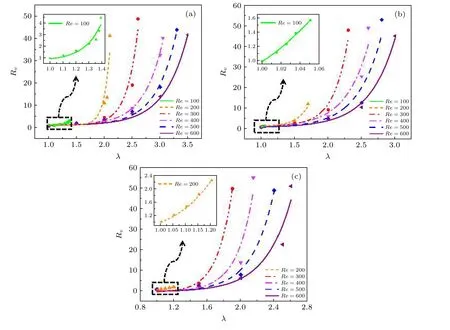
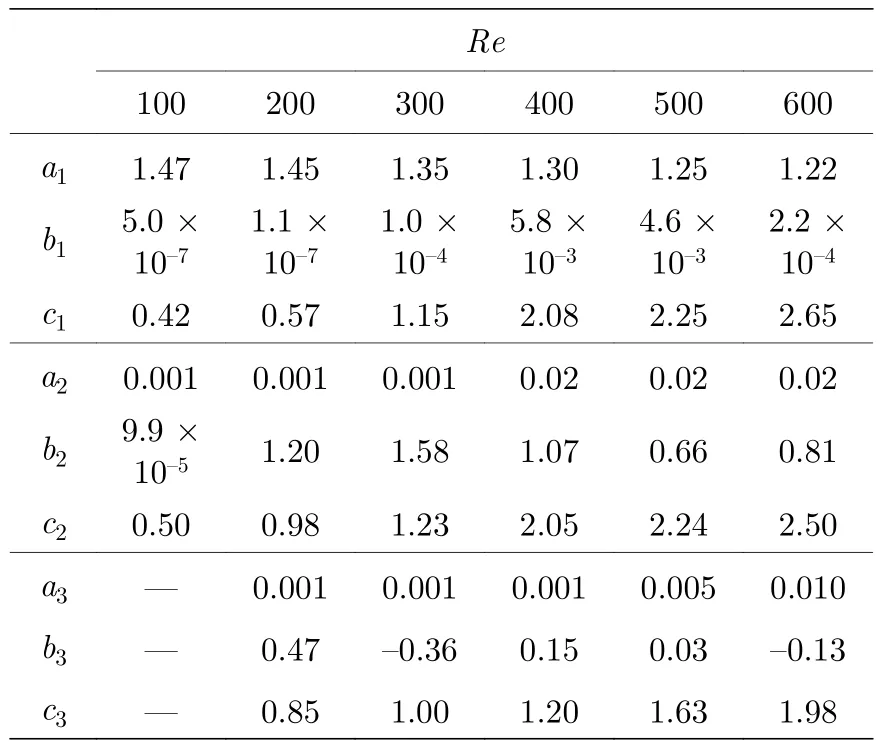
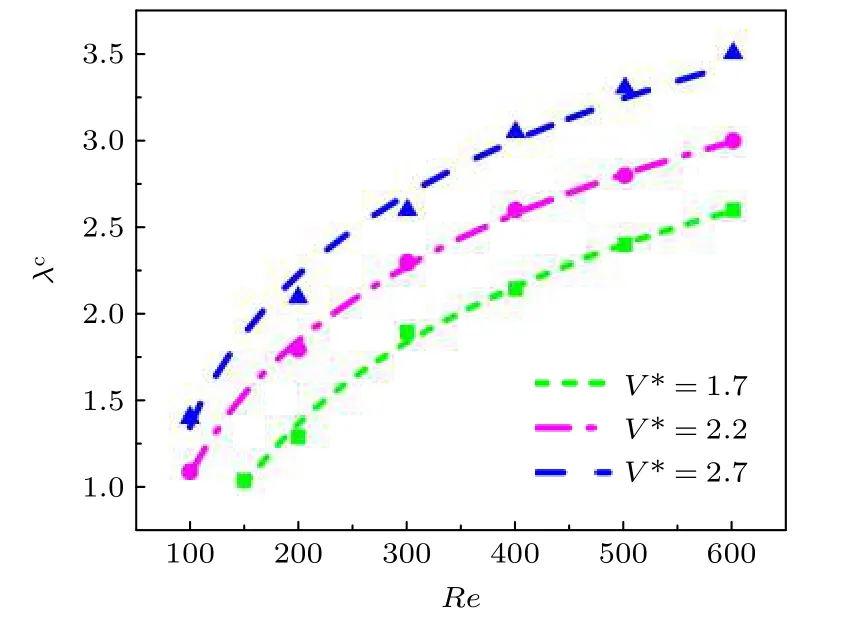
VOF模型被广泛应用于两相流的数值研究,通过引入一个函数C来表示被追踪相的局部体积分数,C=1表示单元格内充满该追踪相,C=0表示充满另一相,0 通过这种处理,两相的质量是守恒的,两相流动问题可以用单相公式来求解.对于牛顿流体和层流,连续性方程和动量方程可写为 式中FS为表面张力.流体的密度ρ和黏度系数µ由各单元体中气相和液相的体积分数加权平均值决定: 其中下标“g”“l”分别表示气体和液体.采用连续表面力模型[26](CSF模型)来求解表面张力FS,应用于体积分数梯度ΔC不等于0的单元体中,其求解方式如下: 其中σ为表面张力系数,κ为界面曲率. 通道内壁采用无滑移边界条件,水和空气分别设置为第一相和第二相.取静态接触角为180°,表明液相可充分润湿壁面.采用稳态单相流作为初始条件,入口设置为压力入口条件,其压力为标准大气压.出口为速度出口条件,通过改变出口截面垂直方向上的平均速度来调节主通道的雷诺数. 在数值模拟中,采用Ansys Fluent 17.0[27]中的基于压力的有限体积法(FVM)求解体积分数方程和动量方程,压力速度耦合插值采用PISO算法,采用Green-Gauss Node Based方法对标量梯度进行离散以提高计算精度.动量方程的离散化采用一阶迎风格式,采用Geo-Reconstruct方法保持界面的高分辨率,压力离散采用PRESTO格式,动量离散采用QUICK格式.为保证计算准确性,在计算中采用较小的时间步长(全局Count数始终小于0.1),其物理时间范围为1 × 10–9—1 × 10–7s. 为了验证本文所用物理模型在三维Y型通道中的准确性,模拟了孤立气泡通过Y型通道并破裂的整个运动过程.本次模拟依据Xu等[28]的实验条件进行设置,一个孤立气泡(长度为1.533 mm)在距离Y型通道(横截面宽度为400 µm,高度为50 µm)入口为6W的位置开始随液相(毛细数为8.493 × 10–4)向右运动,进入Y型分岔口逐渐破裂.如图2所示,将模拟结果与实验结果进行了比较,两者吻合较好,验证了模型的准确性. 图2 气液两相流模型的验证:数值结果与实验结果的比较[28]Fig.2.Validation of hydrodynamic model:Comparison between numerical results (by present model) and experimental results[28]. Y型微通道的计算域采用结构化网格,形成接近正方体的网格单元,如图1(b)所示.网格沿径向由管道中间区域到壁面逐渐细化,采用Gupta等[29]的建议,加密壁面相邻区域网格至5层以上来更好地捕捉气泡与壁面间存在的薄液膜区域.为减小计算量,将矩形通道分为上下对称的两部分,取上部划分网格进行计算.此外,体积分数梯度计算中的微小误差可能会导致在低雷诺数情况下,表面张力不完全垂直于界面从而产生虚假速度,故采用一种移动参考系的方法[30]来抑制虚假速度对结果的不利影响,参考系移动速度为1 m/s. 进一步对不同尺寸范围(从499890到2401453)的网格进行了无关性验证,以确定合适的网格尺寸.首先设定初始的气泡无量纲长度l∗(l/W) 为2.64,选取主通道雷诺数分别为100和600时,气泡前端即将进入Y型分岔口时(达到水动力平衡)的长度来进行比较.如表2所示,以网格4为基准,网格2和3的气泡长度偏差小于0.27%,可以忽略不计,网格1由于偏差过大则不予考虑.其次还对气泡进入Y型分岔口后的轮廓进行了对比,如图3所示(无量纲时间t∗=27.8),气泡轮廓随着网格总数的增大而收敛,当网格数达到1003170时,计算结果随网格总数的增大变化不大.根据上述网格无关性检测,并充分考虑随着网格的细化而增大的计算代价,最终选取尺寸为1003170的网格进行数值模拟. 表2 网格无关性验证:气泡长度对比Table 2.Mesh-independent study:Comparison of bubble length. 图3 网格无关性检验:t∗=27.8时的气泡轮廓Fig.3.Mesh independence study:Bubble profile at the dimensionless time instant of 27.8. 气泡在进入Y型分岔之前,在液相的推动下沿主通道运动,经过一段距离达到稳定状态后,形成弹状气泡,并持续向右移动.进入分岔后,在液相和通道结构的共同作用下破裂,根据气泡轮廓的演变,其破裂过程可分为延伸、挤压和快速破裂[17,31]3个阶段. 图4(a)展示了低雷诺数(Re=100)下,气泡在破裂过程中的形态演变与速度云图.在t∗=23.5时,气泡前端开始进入分岔处,由于Y型结的突然扩张,气泡前端不再受到壁面的束缚,其曲率变大,并不断向两侧通道扩张(t∗=23.5—24.4).这段时间定义为延伸阶段[17],其显著特点是气泡前端不受壁面的影响自由扩张.气泡随着液相继续向两端运动,颈部逐渐变细(t∗=24.4—26.5).这段时间被定义为挤压阶段[31],特点是气泡颈部外侧曲率变化不大且无凹陷.随后气泡颈部宽度进一步下降,颈部外侧原来光滑的曲线变为向尖锐壁面凹陷(t∗=26.5).在液相挤压力、表面张力和Y型分岔尖角的作用下,气泡颈部宽度迅速减小,直至气泡破裂(t∗=26.9),这段时间被定义为快速破裂阶段,特点是气泡颈部曲率剧烈变化,液相作用程度大大增强.图4(b)展示了较大雷诺数(Re=300)下,气泡在破裂过程中的速度云图.在该情况下,可以清楚地看到气泡在经历延伸阶段(t∗=25.5—26.4)后,极快地通过挤压阶段(t∗=26.4—27.3),然后进入快速破裂阶段(t*=27.3—28.6).将气泡进入挤压阶段到快速破裂阶段结束定义为气泡在分岔口的停留时间Δt∗,通过对比发现Re=300时的停留时间(Δt∗=2.2)要小于Re=100时的停留时间(Δt∗=2.5).这是由于液相的挤压力和剪切力随雷诺数的增大而增大,使气泡可以快速通过挤压阶段,进入快速破裂阶段,从而更快地破裂. 图4 Y型分支微通道中气泡轮廓的演化 (a) Re=100,λ=1;(b) Re=300,λ=1;(c) Re=300,λ=2;(d) Re=300,λ=4Fig.4.Evolution of bubble profile in Y-junction region:(a) Re=100,λ=1;(b) Re=300,λ=1;(c) Re=300,λ=2;(d) Re=300,λ=4. 流量比不同时,气泡的破裂过程也不同.如图4(c)所示(λ=2),由于下方分支通道的流速较大,气泡在延伸阶段(t∗=26.9—28.1)逐渐向下方通道运动,随后气泡碰到通道壁面进入挤压阶段(t∗=28.1—28.9),其两端继续向下游通道伸展,形成了不对称的心形.随着时间的推移,气泡颈部逐渐变薄(t∗=28.9—30.3),直至破裂并形成两个体积不同的子气泡.进一步增大流量比,如图4(d)所示(λ=4),发现气泡在还未进入Y型结时,其前端就不再关于中轴线对称,而是向下方偏移(t∗=27.3),进入Y型后其前端完全朝向下方通道(t∗=28.2).紧接着,气泡继续随着液相沿支通道方向伸展,进入下方通道的气泡体积远大于上方通道中的体积,在界面张力的作用下,整个气泡随着液相进入流量较大的下方通道(t∗=29.3—29.9).对比图4注意到,当两支通道的流量相等时,气泡对称破裂并形成两个完全相同的子气泡;当两支通道的流量不均匀时,气泡非对称破裂并形成体积不同的子气泡;当两支通道的流量比足够大时,气泡不再破裂并全部进入流速更大的分支通道. 通过数值模拟可观察到Y型结处4种不同类型的气泡破裂模式:隧道-隧道破裂、阻塞-阻塞破裂、隧道-阻塞破裂和不破裂.在模拟中,通过改变雷诺数、出口流量比和气泡初始尺寸可以观察到这4种破裂模式,如图5所示. 1)隧道-隧道破裂.如图5(a)所示,在分岔的尖角处,由于液相的推动,气泡在挤压力、剪切力和尖角的共同作用下逐渐变形,在快速破裂阶段对称地破裂为两个大小相等的子气泡,随后分别进入下游分支通道.该破裂模式最显著的特点是在气泡的整个破裂过程中,气泡与通道壁面之间存在间隙,主要受液相的挤压力和剪切力作用. 图5 气泡的4种破裂模式 (a) 隧道-隧道破裂;(b) 阻塞-阻塞破裂;(c) 隧道-阻塞破裂;(d) 不破裂Fig.5.Different flow patterns of bubble breakup:(a) Tunnel-tunnel breakup;(b) obstruction-obstruction breakup;(c) tunnel-obstruction breakup;(d) non-breakup. 2)阻塞-阻塞破裂.如图5(b)所示,类似于隧道-隧道破裂,气泡进入Y型分岔后,会在液相和尖角的共同作用下变形.随着时间的推移,气泡的颈部不断变薄并最终破裂成两个大小相等的子气泡.与隧道-隧道破裂不同的是,气泡与通道壁面之间没有间隙,主要受液相的挤压力作用. 3)隧道-阻塞破裂.如图5(c)所示,当流量比增大后,气泡的破裂模式为隧道破裂和阻塞破裂的结合.与前两者不同的是,气泡在延伸阶段就已经部分进入流量较大的通道,流量小的分支通道中,气泡与壁面之间有间隙,受挤压力和剪切力作用;流量大的分支通道中,气泡与壁面之间没有间隙,主要受液相的挤压力作用. 4)不破裂.如图5(d)所示,气泡运动至分岔处,流量大的下侧通道中气泡体积更大,大气泡在表面张力的作用下拖拽小气泡向下运动,使已经进入上侧通道的气泡退出并进入下侧通道.不同于以往将气泡不破裂后的流向归因于Rayleigh-Plateau不稳定性[18],该破裂模式最显著的特点是气泡的流向具有选择性,会进入流量较大的分支通道. 气泡在隧道破裂和阻塞破裂中主要受液相的挤压力和剪切力作用.如图6所示,挤压力主要分布在气泡尾部,表现为气泡前后压降的大小,由于气泡阻塞通道使下游液相的流速减小,阻塞-阻塞破裂的压降(575 Pa)小于隧道-隧道破裂的压降(690 Pa).由于液相通过隧道时的速度梯度较大,气泡在隧道破裂中受剪切力(125 Pa)作用明显,如图6(a)所示.而在阻塞破裂中气泡与壁面之间无剪切力分布,剪切力只出现在气泡与壁面接触界面的两端,对气泡破裂的促进作用较小,如图6(b)所示.对于隧道-阻塞破裂,有隧道的一侧压降大(805 Pa),受剪切力(150 Pa);阻塞的一侧压降小(460 Pa),气泡与壁面间无剪切力. 图6 液相的挤压力和剪切力分布 (a) 隧道-隧道破裂;(b) 阻塞-阻塞破裂;(c) 隧道-阻塞破裂Fig.6.Liquid-phase squeezing pressure and shear force distribution during bubble motion:(a) Tunnel-tunnel breakup;(b) obstruction-obstruction breakup;(c) tunnel-obstruction breakup. 基于Ma等[17]对Y型通道中液滴破裂模式的分类,图7展示了不同流量比下气泡破裂模式的分布.从图7可以看出,雷诺数、气泡尺寸和流量比对气泡的破裂模式有明显的影响.保持气泡尺寸不变,增大雷诺数或保持雷诺数不变,增大气泡尺寸,气泡都会由不破裂趋向于破裂:流量比为1时(图7(a)),气泡沿不破裂、隧道-隧道破裂和阻塞-阻塞破裂方向转变;流量比大于1时(图7(b)—(d)),气泡沿不破裂、隧道-隧道破裂和隧道-阻塞破裂方向转变.这是因为雷诺数的增大会使液相的推动力和剪切力增大,相对而言表面张力的作用减小,气泡更容易破裂;气泡尺寸的增大会使隧道逐渐消失,气泡堵塞通道也促进了破裂.这种过渡规律也类似于Wang等[32]在非对称T型通道中观察到的气泡破裂和Jullien等[33,34]在对称T型通道中观察到的液滴破裂.此外,气泡破裂的不均匀性随着流量比的增大而增强,若保持雷诺数和气泡尺寸不变,增大流量比,气泡沿隧道-隧道破裂/阻塞-阻塞破裂、隧道-阻塞破裂和不破裂方向转变. 图7 不同流量比下气泡的破裂模式相图 (a) λ=1.0;(b) λ=1.5;(c) λ=2.0;(d) λ=2.5Fig.7.Bubble breakup modes at different flow ratios:(a) λ=1.0;(b) λ=1.5;(c) λ=2.0;(d) λ=2.5. 由图4气泡的破裂过程(Re=300)可知出口流量比对气泡破裂后的体积分布有着显著的影响,基于此对子气泡体积比(Rv)与出口流量比(λ)之间的关系进行研究.如图8所示,子气泡的体积比随流量比的增大而单调增大,且呈指数增长趋势.这与前文所得到的结论一致,由于下方通道的流量增大,气泡在延伸阶段更多地进入下方通道,破裂后的体积比相应增大,当流量比接近临界值(气泡不破裂)时,子气泡体积比接近于无穷. 图8(a)给出了在气泡尺寸V∗=2.7时,主通道雷诺数对子气泡体积比的影响.从图8(a)可以看出,随着雷诺数的增大,子气泡体积比随流量比变化的幅度逐渐减小,曲线逐渐平缓.这是由于雷诺数越大,气泡在Y型分岔口停留的时间(Δt∗)越短,气泡随液相流入下端的体积越小(相较于小雷诺数下气泡流入下端的体积),破裂后子气泡的体积相差越不明显.此外,由于雷诺数较小(Re=100)时气泡的停留时间较长,对流量比的变化也更为敏感,气泡在流量比为1.4时就不破裂(与图8(b),(c)中雷诺数分别为100和200时的情况类似). 图8 不同流量比(λ)下分支通道中子气泡的体积比(Rv) (a) V∗=2.7;(b) V∗=2.2;(c) V∗=1.7Fig.8.Volume ratio (Rv) of daughter bubbles in branching channel with different outlet flow ratio (λ):(a) V∗=2.7;(b) V∗=2.2;(c) V∗=1.7. 在不同的无量纲尺寸下,子气泡体积比与出口流量比之间依然遵循着与V∗=2.7时相似的指数变化趋势.但随着气泡尺寸的减小,相同雷诺数下气泡可以破裂的流量比范围减小,流量比对气泡破裂的影响愈加明显,表现为增长的趋势逐渐变陡.这是由于气泡尺寸越小,液相挤压力和剪切力的作用面积越小,在表面张力不变的情况下气泡越不容易破裂. 基于子气泡体积比的指数增长趋势,提炼出了不同雷诺数下子气泡体积比(Rv)与出口流量比(λ)的对应关系: 其中a,b,c为拟合参数,具体数值如表3所示.该幂律关系在雷诺数为100—600的情况下具有较好的准确性,可用于预测不同流量比下气泡破裂后的体积分布. 表3 经验公式(11)的拟合参数值Table 3.Fitting parameter values of empirical formula (11). 通过以上分析可以发现,存在一个临界流量比λc,当等于或大于临界流量比时,气泡不破裂并完全进入下游通道;当流量比低于临界值时,气泡破裂并分别流向上下分支通道.图9给出了雷诺数(100—600)和临界流量比之间的关系.随着雷诺数的增大,气泡需要更大的流量比才能完全流入一侧通道(这与梁宏等[6]的结论是一致的).对比发现,在相同的雷诺数下,临界流量比随气泡尺寸的增大而增大,这与前文结论一致.3种气泡尺寸下,临界破裂流量比随雷诺数变化的趋势是相似的,且符合以下幂律关系: 图9 不同气泡尺寸下的临界破裂流量比(λc)Fig.9.Critical fracture flow ratio (λc) at different bubble volume. 其中i和j为拟合参数,具体数值如表4所示.通过应用该幂律公式,即可得到气泡可破裂的流量比范围. 表4 经验公式(12)的拟合参数值Table 4.Fitting parameter values of empirical formula (12). 本文基于VOF方法建立了三维Y型微通道中的气液两相流模型,重构了微通道内非均匀出口流量引起的气泡非对称破裂过程,系统研究了不同出口流量比、雷诺数以及初始尺寸下气泡破裂的动力学特征并定量描述了破裂后子气泡体积受以上3个参数的影响规律,获得以下主要结论. 1)气泡非对称破裂过程分为3个阶段:延伸阶段、挤压阶段和快速破裂阶段.在延伸阶段,气泡与分岔通道尖角处壁面无接触,自由扩张;在挤压阶段,气泡颈部外侧为光滑曲线;在快速破裂阶段,气泡颈部外侧曲率改变,液相作用程度增大.在气泡初始尺寸较小或出口流量比较大的情况下,气泡不破裂,只经历延伸阶段和挤压阶段. 2)气泡的破裂模式可分为隧道-隧道破裂、阻塞-阻塞破裂、隧道-阻塞破裂和不破裂4种典型模态.出口流量比为1时,气泡的破裂过程总是对称的.气泡尺寸较小时(V∗≤ 2.2)为隧道-隧道破裂,尺寸较大时(V∗>2.2)为阻塞-阻塞破裂.随着出口流量比的增大,气泡的破裂过程逐渐变为非对称破裂,其破裂模式逐渐向隧道-阻塞破裂和不破裂方向转变. 3)获得了不同雷诺数和初始气泡尺寸下,气泡破裂后子气泡体积比随出口流量比的变化规律并提炼了相应的准则关联式.由于子气泡体积比随出口流量比的增大而单调增大,因此可通过调节出口流量比可精确控制子气泡的尺寸.此外,定量获得了不同雷诺数与初始气泡尺寸下,气泡破裂与否的临界流量比.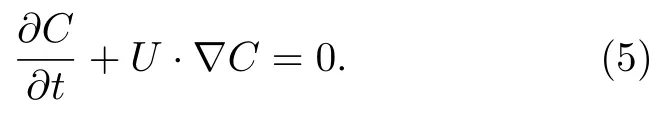
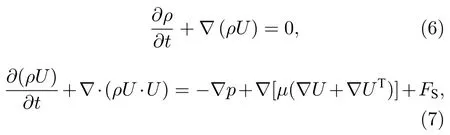
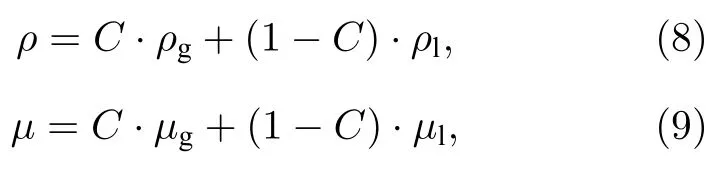
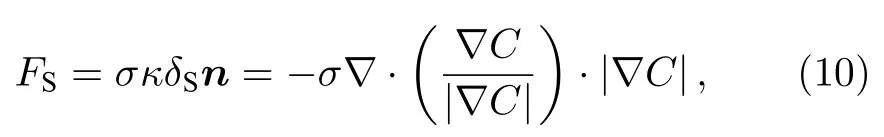
2.3 边界条件
2.4 模拟方法
2.5 模型和网格无关性验证


3 结果与讨论
3.1 气泡在Y型通道中破裂的动态过程
3.2 气泡在Y型通道中的破裂模式


3.3 气泡非对称破裂后的体积分布
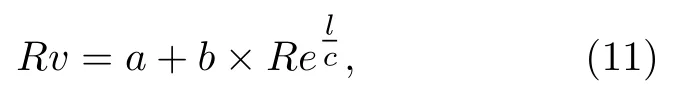
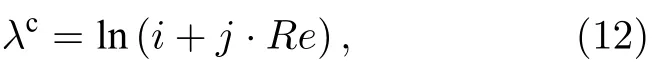

4 结论

