基于间隙度量的多模型过热汽温预测控制

齐卫祎，邓拓宇

（华北电力大学 控制与计算机工程学院，河北 保定 071003）

0 引 言

随着2030年“碳达峰”目标的提出，大力发展新能源发电已经成为必然。新能源发电存在随机性与不稳定性，需要火电机组来承担更多深度调峰的任务。传统的火电机组主汽温串级控制器的控制参数是在一定工况下整定得来的。当机组处于深度调峰的变负荷工况下，机组的运行参数变化幅度较大；同时，汽温对象本身具有大惯性、时滞性特性，再加上扰动的影响，这些因素会导致系统控制品质的恶化，使得过热汽温的动态偏差易超过允许安全范围，进而影响整个火电机组的安全运行[1]。

由于传统的PID串级控制难以适应当前机组深度变负荷的情况，故诸多先进的控制策略被引入主汽温控制中来，如模糊控制[2]、自抗扰控制[3]、神经网络控制[4]和预测控制[5-6]。预测控制[7]自被提出以来，已经在复杂工业过程中取得广泛的应用，其在处理工业过程中的大迟延、大惯性问题时显示出强大的优势[8]。

目前，有关学者已经对预测控制在主汽温调节中的应用做了大量的研究。文献[9]提出了一种基于ARX-Laguerre预测模型的预测控制算法，把PID控制器的性能指标引入到预测控制的优化指标中去，通过在线最小二乘辨识来提升系统的自适应性。文献[10]将迭代预测控制器引入过热汽温控制中，通过历史误差来修正控制器，实现了模型失配情况下的设定值跟踪。文献[11]提出了多模型切换的预测控制方法，即根据不同工况预先设计不同的控制器，再在变负荷时切换到最匹配的预测函数控制器。文献[12]提出了一种基于RBFNN的PFC控制策略，即通过径向基神经网络实时辨识被控对象来克服被控对象的时变；但文中方法神经网络在线计算量大，不易于实际应用。文献[13]提出了主汽温多模型预测控制策略，各控制器的权值计算方法是：计算实际汽温与预测汽温的差值，然后用递推贝叶斯公式计算得到各子模型与实际被控模型的匹配概率。文献[14]将PI控制与隐式GPC算法相结合，增强了控制器的鲁棒性。文献[15]基于多模型切换的锅炉汽温预测控制，首先选取多个典型工况设计动态矩阵控制器，通过各子模型输出与实际输出的误差计算 ITAE性能指标，并将其作为子控制器的切换准则；但该方法使用时需要选取的子模型足够多，否则各控制器在切换时会引入控制输出的振荡。

间隙度量理论能准确地描述不同模型之间的动态特性差异。本文提出基于间隙度量理论的多模型过热汽温预测控制策略：根据若干典型工况的固定模型，设计相应的局部控制器，计算得到每一个时刻的控制增量；通过间隙度量理论加权各个局部控制器在该时刻的控制增量，得到该时刻总控制增量并作用到被控对象上。仿真结果表明，该方法可以满足火电机组全工况运行的要求。

1 过热汽温喷水减温控制系统

过热汽温控制系统由汽包、一级过热器、屏式过热器、二级过热器和2级喷水减温器组成。

采用2级喷水减温结构对末级出口主汽温进行控制：一级喷水减温起粗调作用，二级喷水减温起细调作用。2个喷水减温系统的原理相同。图1所示为一级喷水减温示意图。

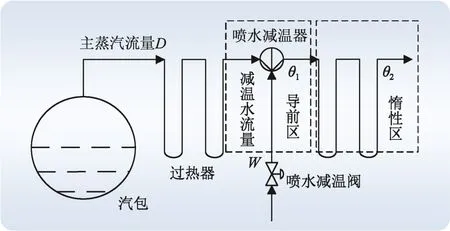
图1 过热汽温控制结构Fig.1 Structure of superheated steam temperature control

通过控制喷水减温阀的开度来控制减温水流量，进而调控过热蒸汽温度。图1中，减温水流量W和喷水减温器出口温度θ1为导前区，θ1到θ2之间的过热器管道为惰性区。

导前区传递函数：

惰性区传递函数：

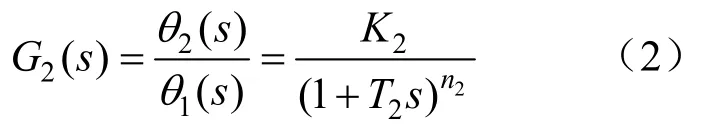
2 多模型预测控制策略

考虑过热汽温对象具有时变性，本文采用多模型切换方法。通过间隙度量理论加权多个控制器的输出。对于大迟延、大惯性的被控对象，采用动态矩阵控制。图2示出本文采用的多模型预测控制策略。

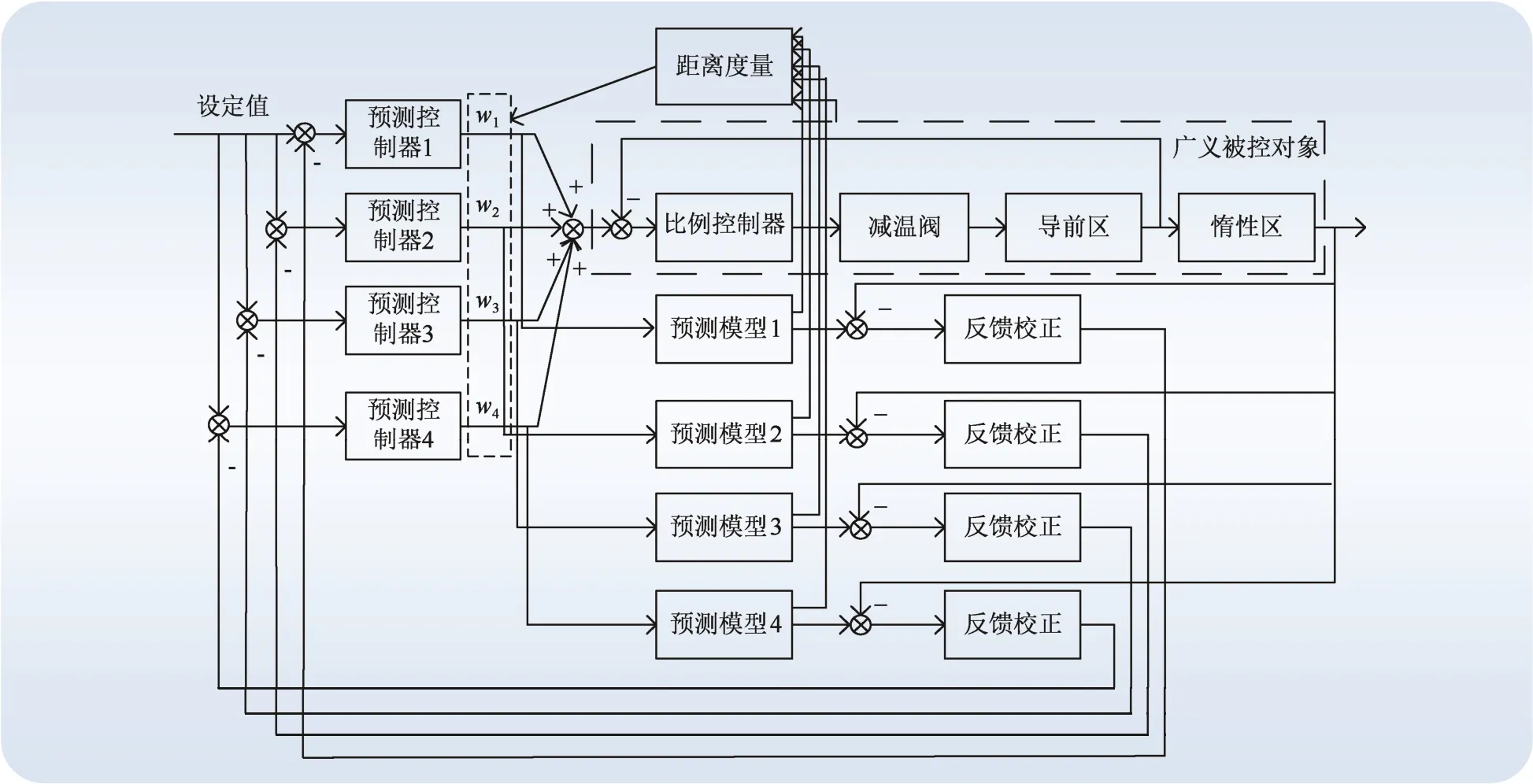
图2 多模型预测控制策略Fig.2 Strategy of multi-model predictive control

首先选取可以覆盖整个电厂负荷变化的4个典型工况。根据这4个典型工况分别建立局部动态矩阵控制器。局部预测控制器输出为当前这个时刻的控制增量Δui(k)(i=1,2,3,4)。当负荷偏离这4个典型工况点的时候，通过间隙度量理论计算当前工况偏离4个典型工况的程度，求得4个局部预测控制器的控制量权重wj(j=1,2,3,4)。

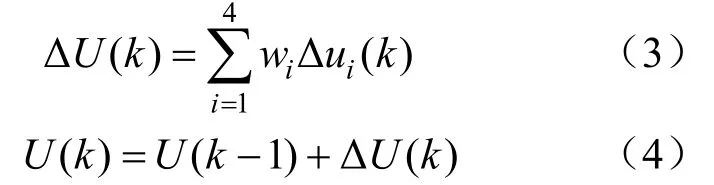
2.1 多个子模型的选取

对于过热汽温被控对象，影响模型参数变化最大的扰动是负荷变化。当火电机组负荷变化的时候，机组的燃煤量和给水量都会相应的发生变化。机组给水量的变化会影响过热器中的换热，导致过热汽温发生变化；机组的燃煤量发生改变以后，直接改变产生的热量，使得烟气温度变化，导致过热汽温改变。所以，需要选取几个典型工况下的过热汽温被控对象，建立模型集。

文献[16]给出了在4个典型工况下，过热汽温被控对象导前区和惰性区的传递函数，如表1所示。

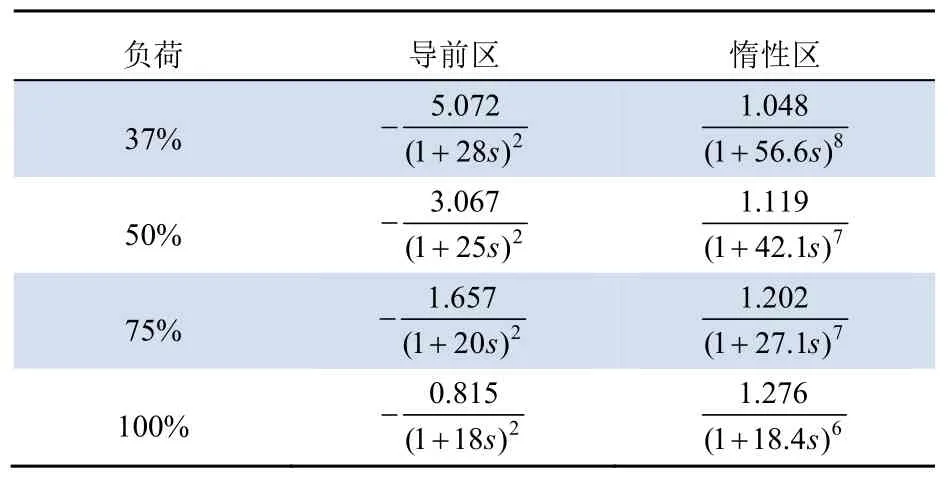
表1 不同负荷过热汽温参数Tab.1 Parameters of superheated steam temperature under different loads

2.2 多模型切换控制权重的确定

本文采用间隙度量理论[17]计算不同负荷下被控对象之间的距离，从而确定各控制器的输出权重。

假设M，N为巴那赫空间Z中的2个线性子空间。若K(s)是传递函数矩阵，则可以得到其正规化右互质分解：

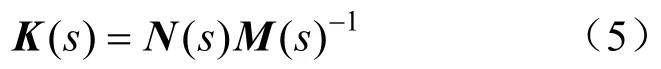
线性模型K1和K2之间的间隙度量值：

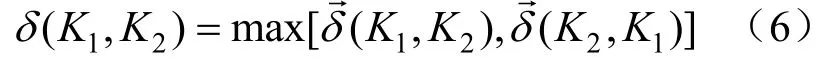
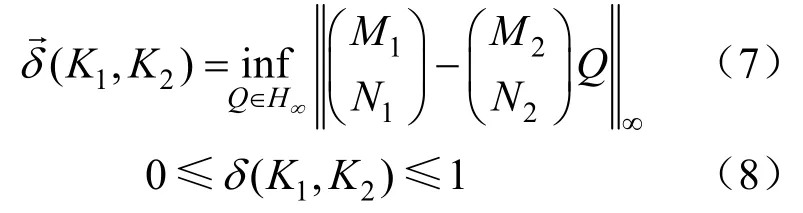
2个传递函数越相似，则间隙度量值越接近于0。间隙度量值与工况的相似程度呈反比。通过间隙度量值来确定各个控制器输出的权重：

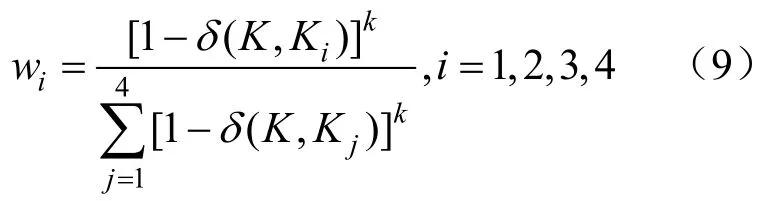
由式（9）可知，当运行工况接近某一工况的时候，则该工况的局部控制器输出最大。k为可调参数，k大于等于1，通过k以调整输出的权值。

2.3 动态矩阵控制

动态矩阵控制是一种基于系统阶跃响应的预测控制算法。因其以被控对象的阶跃响应系数为模型，所以避免了通常的传递函数模型参数的辨识过程，从而减少了计算量。采用多步预估技术能有效解决被控对象的迟延问题；按照使预估输出和给定值偏差最小的二次性能指标来计算控制增量，从而实现最优控制；通过计算预测值和实际的偏差，不断校正每一步的预测值，构成一个闭环，增强系统的稳定性。

2.3.1 预测模型

图3为被控对象的阶跃响应曲线图。对象的动态特性通过单位阶跃响应在采样时刻的值来描述，如a1,a2,···,ap。p为模型的时域长度，ap为接近稳态值的系数。

图3 被控对象阶跃响应Fig.3 Step response of the controlled object

通过阶跃响应可以采样得到p个时刻的采样值，进而可以构建反映系统动态特性的动态矩阵A。根据线性系统叠加的原理，可以由给定输入的增量来预测系统未来的输出。

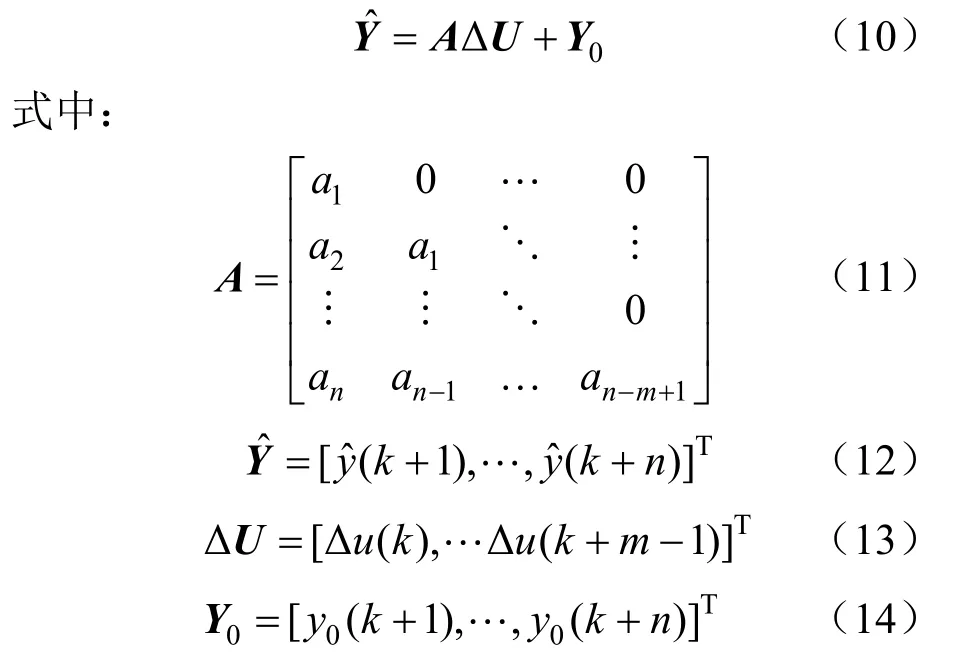
式中：n为最大预测长度；m为控制长度；ΔU为控制增量；Y0为控制作用保持不变时的初始预测值；为n步预测值。

2.3.2 滚动优化

滚动优化的目的是为了使输出预测值逼近设定值，并且尽可能减少控制量的波动。如式（15），构建二次性能指标函数来求取使得误差最小和控制量最小的控制增量。

式中：q(j)为误差的加权；r(j)为控制增量的加权。

将式（15）用向量形式表示：

式中：W为设定值的向量形式；Q误差加权矩阵；R为控制增量加权矩阵。

通过偏导为零求取极值点，获得控制增量值。

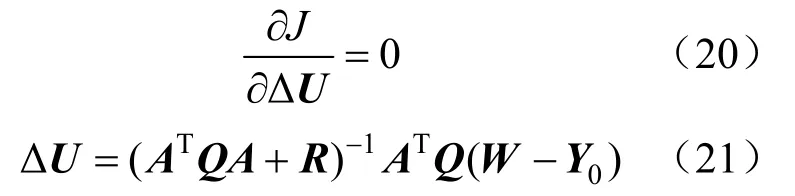
优化过程不是一次完成的。每次计算出最优控制增量以后，取当前的控制增量施加控制；每一步控制量只取当前的控制增量，滚动进行优化。

2.3.3 误差校正

由于实际运行中系统会存在扰动，使得预测值和对象的实际值产生较大的偏差，所以引入误差校正。

式（22）为k+1时刻实际输出和预测输出构成的预测误差。

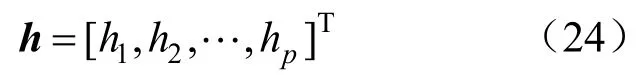
式中：h为误差校正向量。

在k+1时刻，时间基点的变动导致预测未来时间点也将移动到k+2,···,k+1+N；因此k+1时刻的初始预测值可以通过校正后预测值移位得到。

误差反馈校正的引入，使系统成为一个反馈控制系统，提升了系统的稳定性。

3 仿真实验

为了验证本文提出的多模型预测控制策略的有效性，通过 MATLAB进行仿真分析：分别与PID串级控制、单模型预测控制进行对比，从稳态性能、动态性能角度进行分析。

过热汽温模型的内回路采用比例控制，可以快速消除内回路的扰动。通过 ZN整定法求取比例系数。将整定好的内回路与惰性区传递函数作为广义被控对象，对其进行控制器的设计。多模型预测控制选用表1的4个典型工况作为预测模型。构建动态矩阵，建立4个局部动态矩阵控制器。控制器参数为采样时间T=5 s，预测步长P=200，控制步长M=10，误差加权矩阵Q=IP×P，控制量加权矩阵R=IM×M，误差校正向量hi=1(i=1,···,P)。

3.1 定负荷情况

当机组运行在典型工况负荷下，多模型预测控制与单模型预测控制效果一致。将多模型预测控制与PID串级控制进行比较。

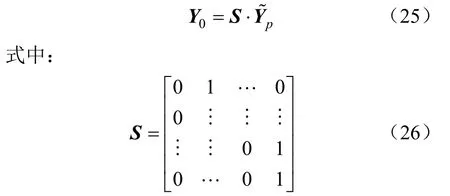
在负荷37%、50%、75%、100% 4种典型工况下，分别进行设定值阶跃变化实验。设定值起始值为10，在2 500 s变为5，仿真时间为5 000 s。PID串级控制的主控制器的参数采用ZN整定法。各负荷下，PID串级控制的主控制器参数如下：在 37%负荷时，Kp=0.97，Ti=541.1，Td=135.27；在 50%负荷时，Kp=0.99，Ti=371.69，Td=92.92；在 75%负荷时，Kp=0.95，Ti=251.03，Td=62.76；在100%负荷时，Kp=1.05，Ti=161.33，Td=40.33。图4所示为2种控制方法的仿真结果。

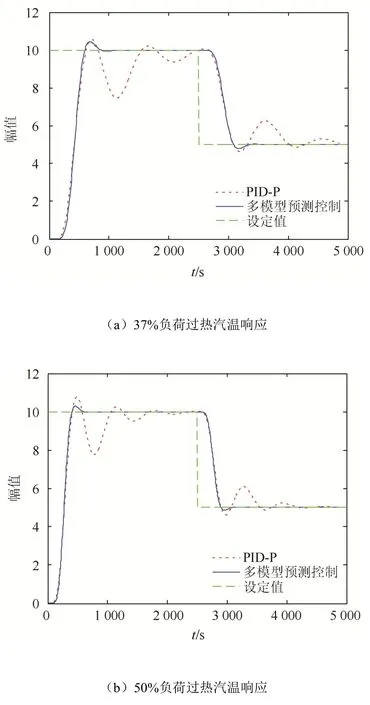
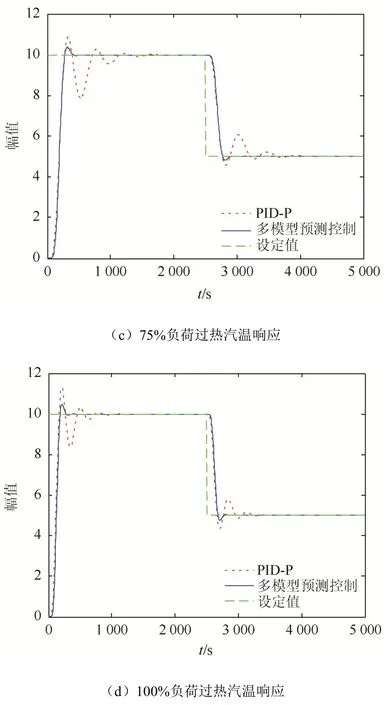
图4 各典型工况阶跃变化仿真曲线Fig.4 Simulation curves of step changes under typical operating conditions

参考图4，对比不同负荷下多模预测控制相较于 PID串级控制的超调量与调节时间：在37%负荷下，多模型预测控制的超调量为4.48%，减少了1.17%，调节时间为780 s，减少了1 570 s；在50%负荷下，多模型预测控制的超调量为3.06%，减少了4.63%，调节时间为685 s，减少了920 s；在75%负荷下，多模型预测控制的超调量为3.76%，减少了4.91%，调节时间为360 s，减少了720 s；在100%负荷下，多模型预测控制的超调量为4.90%，减少了8.11%，调节时间为255 s，减少了420 s。

由上可以看出，多模型预测控制的调节时间和超调量都明显小于PID串级控制，显示出更好的动态性能和稳态性能。

3.2 变工况情况

为了验证多模型预测控制在负荷变化时的控制特性，做机组负荷递减时的设定值阶跃仿真实验。假设机组刚开始运行在100%负荷下，在时间2 500 s，5 000 s，7 500 s，机组负荷分别递减为 75%，50%，37%。将获取的系统响应曲线与在 100%负荷下设计的传统串级控制器和单模型预测控制器响应曲线进行对比，如图5所示。

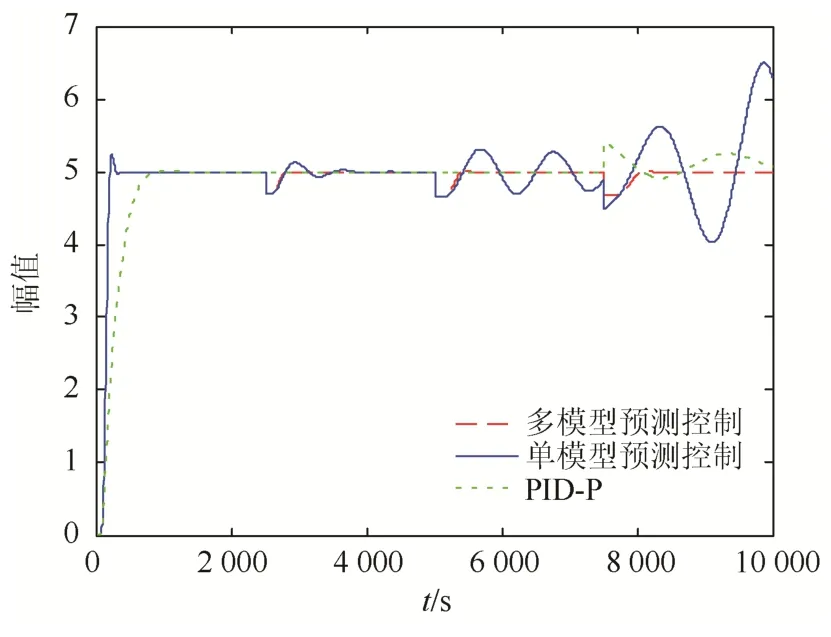
图5 工况递减下不同控制策略阶跃响应Fig.5 Step response of different control strategies under decreasing operating conditions

在机组负荷突变时，被控对象参数的变化导致模型失配，使得被控量发生波动，偏离设定值。由图5可见：多模型预测控制在机组负荷每次骤变之后，能够快速使被控量稳定到设定值；而单模型预测控制随着模型失配程度的增加，在每次机组负荷骤变之后，系统的被控量波动越来越大，系统的稳定性降低；传统的串级控制器由于其鲁棒性，在负荷大范围波动时，控制器可以保证被控值稳定不发散，但随着负荷变化越大，其控制性能开始变差。

考虑到在实际生产过程中，机组多数时间处于小范围负荷波动运行工况，所以做工况小范围波动实验，以观察多模型预测控制、单模型预测控制和PID串级控制对于小范围变工况的适应程度。假设机组在100%负荷稳定，而此时被控对象参数如表1所示。在仿真时间0时刻，负荷发生改变，被控对象参数发生变化：导前区参数K增益变为1.2，时间常数T变为19；惰性区参数保持不变。做设定值阶跃响应扰动实验，阶跃5个单位，获得系统响应曲线如图6所示。

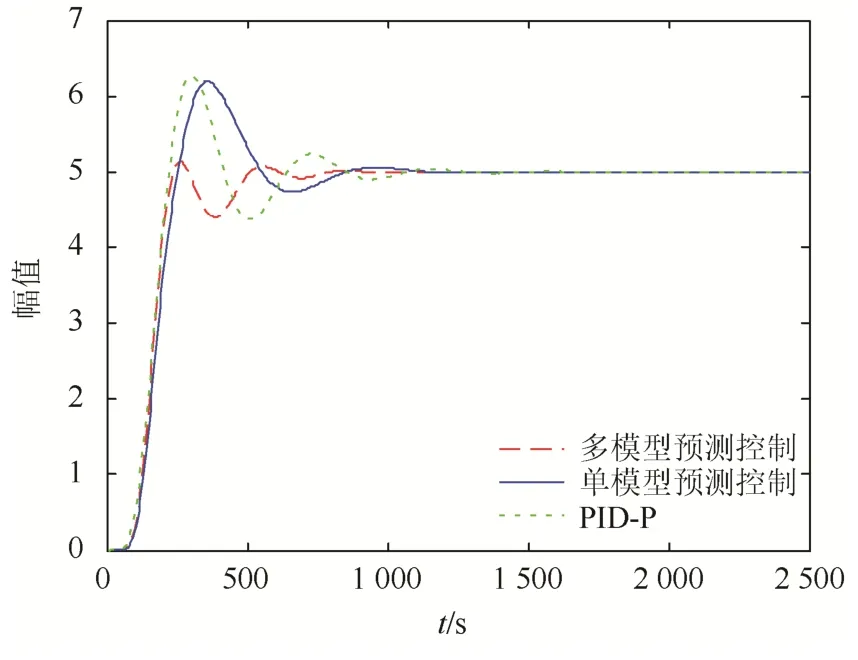
图6 变工况下不同控制策略阶跃响应Fig.6 Step response of different control strategies under variable conditions

由图6可以看出，多模型预测控制的超调量为1.51%，调节时间为480 s；单模型预测控制的超调量为23.92%，调节时间为780 s；PID串级控制的超调量为25.42%，调节时间为805 s。多模型预测控制在变工况的情况下能够更加快速平稳地使过热汽温达到设定值。

可以看出，本文所提出的多模型预测控制能够适应被控对象参数的时变，具有较好的鲁棒性。

3.3 扰动干扰情况

为了验证多模型预测控制的抗干扰性能，选用100%负荷下的过热汽温模型，在2 500 s给设定值加10倍(t)的阶跃扰动，并与PID串级控制进行对比。响应曲线如图7所示。

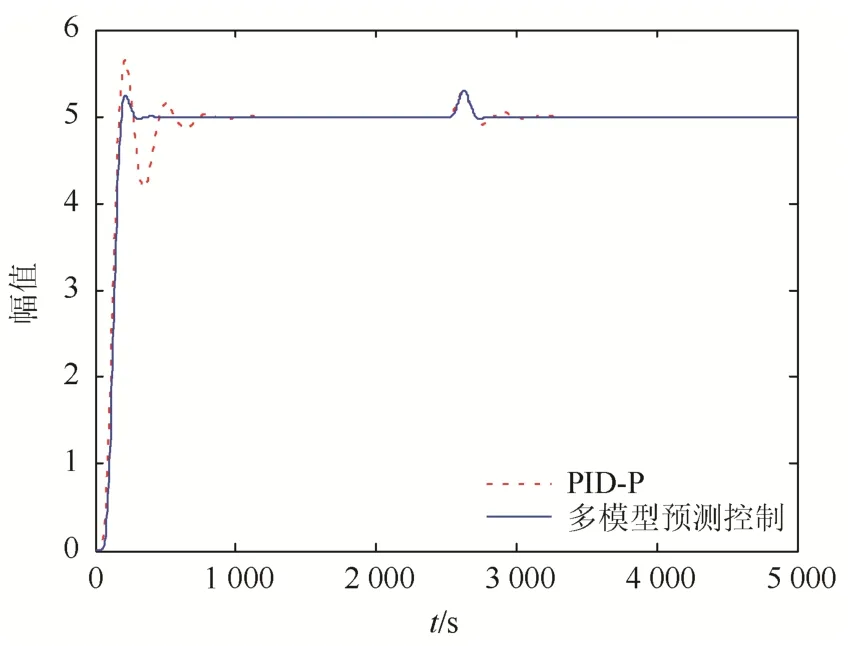
图7 过热汽温输入端扰动阶跃响应Fig.7 Step response of input disturbance of superheated steam temperature

从系统响应曲线可以看出，在系统受到外界干扰的情况下，多模型预测控制和PID串级控制均存在超调现象；但多模型预测控制的调节时间更短，可以使系统更快恢复设定值，拥有更好的抗干扰性能，鲁棒性更强。

4 结论

为应对火电机组深度调峰，提出了基于间隙度量的多模型过热汽温预测控制策略。

（1）在负荷不变的情况，多模型预测控制比PID串级控制更能快速稳定完成对设定值的响应。

（2）在负荷变化的情况下，多模型预测控制可以更好地适应负荷快速变化的情况，使过热汽温稳定在一定范围内。

（3）过热汽温系统输入扰动实验结果表明，相较与PID串级控制，多模型预测控制能够使过热汽温值更加快速回到设定值。