政府碳规制与重污染企业碳减排策略的动态演化博弈仿真分析
陆秋琴,于思颖,黄光球
(西安建筑科技大学 管理学院, 西安 710055)
自1965年以来,全球二氧化碳年排放量不断增加,到目前为止,全球二氧化碳年排放量已达340亿吨[1-2]。大量的二氧化碳排放是导致全球变暖的主要原因之一,为了共同应对全球气候变暖问题,所有国家都应共同承担其中的责任与义务[3-4]。2015年的《巴黎协定》指出,全球气温较前工业化时代的上升幅度应尽量控制在1.5 ℃以内,这进一步明确了全球气候问题的紧迫性和目标[5-6]。作为世界最大的发展中国家,我国的十四五规划制定了“2030年前碳达峰、2060年前碳中和”的目标[7]。因此,对政府来说,制定相应的碳规制政策引导企业积极碳减排十分必要;对企业来说,尤其是重污染企业,实施积极碳减排策略同样迫在眉睫。重污染企业是指从事特定重污染行业,在生产经营过程中可对环境造成严重污染的企业,这类企业往往也是主要的碳排放源之一[8]。因此,如何精准制定相关策略,在保证重污染企业经营的同时,促使企业加快技术升级,实现碳减排目标是亟待解决的难题。
Liu等[9]认为政府会通过碳交易、碳税和碳补贴等碳规制措施来促使企业进行碳减排;孟凡生等[10]通过研究低碳技术创新的投入补贴、碳税和碳排放权交易3种碳规制工具对企业低碳技术创新性的影响,认为政府必要的碳规制策略能够激励企业低碳技术创新;徐建中等[11]通过构建政府绿色创新投入补贴与征收碳税对制造企业绿色创新模式选择影响的演化博弈模型,认为绿色创新投入补贴与征收碳税均能提升企业开展突破式绿色创新活动;王文举等[12]基于有限理性假设,通过构建碳税机制下地方政府与企业减排行为的演化博弈模型,分析碳税税率对博弈双方策略选择的影响,结果表明碳税税率对于碳减排效果有重要影响;朱庆华等[13]通过引入政府动态惩罚和补偿策略来研究政企双方策略的互动机制,研究表明动态策略有助于系统实现Nash均衡;Govinda等[14]研究发现碳税与补贴政策同步实施可以遏制企业收益突降的问题,当碳税收入暂作补贴支出时,理论角度看碳税和补贴政策的共同作用能够提高企业减排的积极性;Asafu-Adjaye等[15]通过分析研究碳交易机制对澳大利亚煤炭及钢铁行业碳排放产生的影响,提出碳交易机制能有效地激励煤炭与钢铁行业碳排放的减少。针对碳减排实施过程中政府与企业的博弈关系,国内外学者主要运用了演化博弈模型和实证研究2种方法进行了研究,皆取得了一定的研究成果。但关于政府碳规制政策的研究不够全面,且研究大多采用静态演化博弈,而政企之间的相互影响并不是一个静态的过程,所以静态演化博弈并不能较好地分析研究此类问题。与之相比,动态演化博弈模型由于可以较好地分析政府与企业之间的互动机制,因此应用较为广泛。但由于动态演化更为复杂,因此模型求解较为困难,而系统动力学是专门处理复杂系统问题的工具,恰好适合于处理博弈双方复杂的动态演化问题[16-17]。
基于此,本文运用系统动力学与演化博弈模型相结合的方法,建立政府碳规制策略与重污染企业碳减排策略的演化博弈模型,全面分析政府的碳惩罚、碳交易、碳税和碳补贴政策与重污染企业碳减排技术创新的演化博弈,通过提出动态惩罚、动态碳价、动态碳税与动态碳补贴策略,并使用VENSIM软件来仿真分析研究系统的Nash均衡点,从而为政府和重污染企业的碳中和目标提供一定的参考。
1 政府与重污染企业演化博弈模型的假设与建立
1.1 演化博弈模型假设
1.1.1博弈参与方
在非信息对称条件下,博弈系统包含政府与重污染企业2个有限理性群体[18]。
1.1.2博弈双方行为策略
基于有限理性假设,政府可采取的策略有“积极碳规制”与“消极碳规制”,重污染企业可采取的策略有“积极碳减排”与“消极碳减排”。本文确定的政府对重污染企业碳规制的策略为:碳惩罚、碳补贴、碳交易与碳税。政府对于重污染企业的碳减排补贴,其本质相当于政府对于碳环境投资,对重污染企业的监督和惩罚机制相当于对碳环境的管理,其目的是实现经济发展与碳环境协调发展,以较低的环境成本获得较高的环境投资效益。碳交易市场是在政府监督下的,对于企业碳减排发挥激励作用的一种清洁发展机制,重污染企业在碳交易机制作用下受制于既定碳配额,超出既定碳配额会有碳交易惩罚成本,否则会有碳交易盈余收入,从而激励重污染企业采取积极碳减排行为策略。重污染企业采取积极的碳减排策略,会产生技术创新投入成本、运营成本与管理成本,影响企业收益,但同时会获得政府补贴与碳交易收益;企业采取消极的碳减排策略,会因碳排放过度产生碳交易成本,并且会损害企业形象,间接影响企业收益。政府与重污染企业双方博弈的成本收益参数假设及解释如表1所示。
1.1.3模型构建及相关参数假设
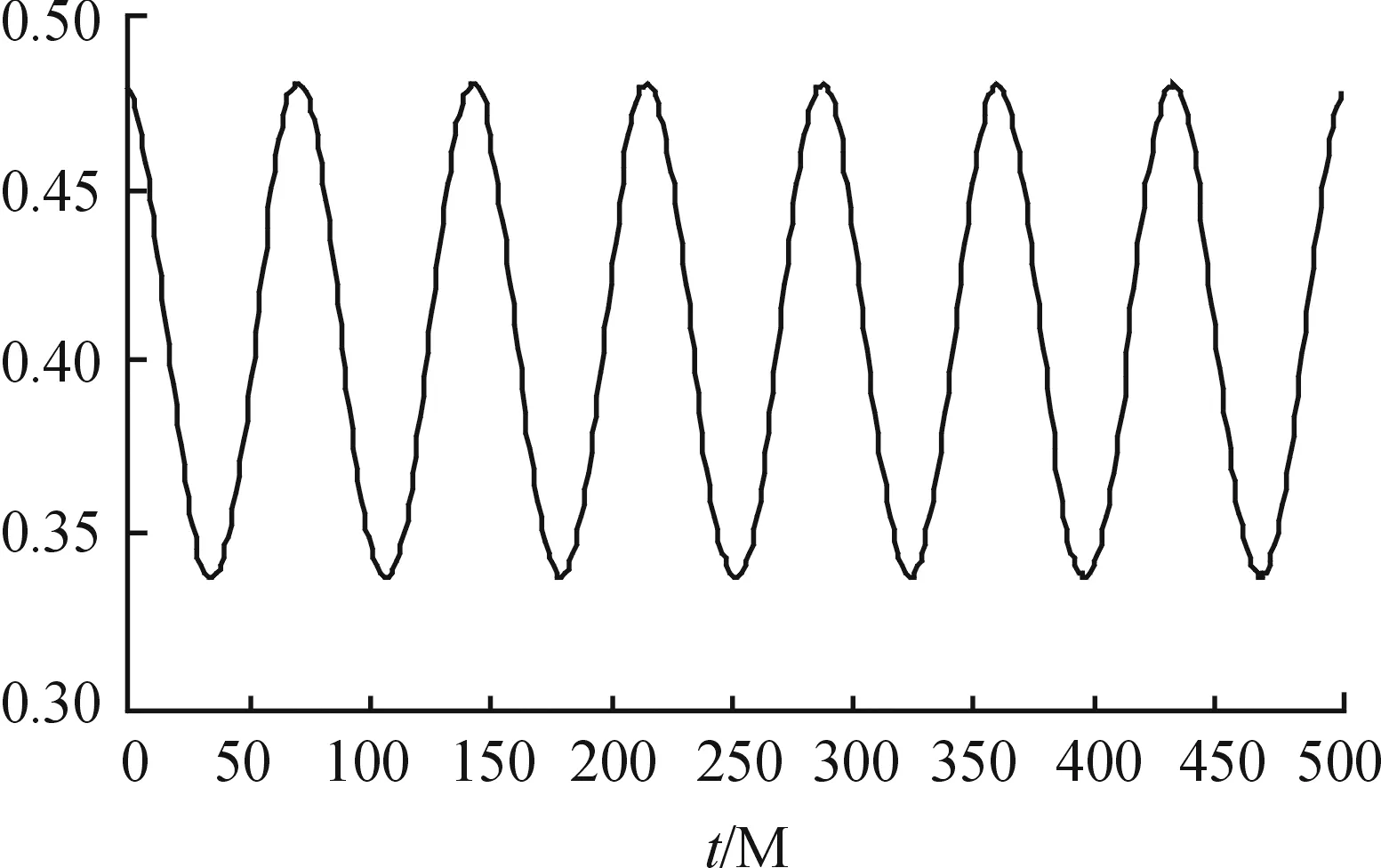
假设1基于重污染企业消极碳减排行为考虑,在碳减排初期,由于技术创新成本投入、碳减排处理成本过高,因此假设企业选择积极碳减排策略时,获得的碳减排收益小于成本,即R′ 假设3政府选择采取积极碳规制的概率为x,选择消极碳规制的概率为(1-x)。重污染企业选择采取积极碳减排策略的概率为y,选择采取消极碳减排策略的概率为(1-y),x(0≤x≤1)和y(0≤y≤1)分别是关于时间t的函数。 表1 博弈双方成本收益的参数假设及解释 根据政府与重污染企业演化博弈模型假设,双方演化博弈策略如图1所示。 图1 政府与重污染企业演化博弈策略示意图 政府与重污染企业博弈收益矩阵效益如表2所示。 表2 政府与重污染企业博弈矩阵收益 由于政府和重污染企业都是有限理性的群体,无法完全理性地判断对方选择的策略,所以依据演化博弈理论可知,政府选择积极碳规制策略、消极碳规制策略以及平均期望的收益分别为: U1M=y[Rg-αI+βQ′-C]+ (1-y)(βQ-C+P)= y[Rg-αI-β(Q-Q′)-P]+ βQ-C+P (1) U1N=yRg+(1-y)(-W)= y(Rg+W)-W (2) (3) 企业选择积极碳减排策略、消极碳减排策略以及平均期望的收益分别: (1-x)(R′-I)=x[αI-βQ′+ (4) (1-x)(R-S)=x[-βQ- (5) (6) 根据复制动态方程原理可得,政府积极碳规制概率为x、重污染企业积极采取碳减排策略概率为y的复制动态方程分别为: x(1-x)(U1M-U1N)= x(1-x){y[-αI-β(Q-Q′)- W-P]+(βQ+W+P-C)} (7) y(1-y)(U2M-U2N)= y(1-y){x[αI+(β+γ)· (Q-Q′)+P]+(R′-R-I+S)} (8) 根据上述动态复制方程可以得到二维动力系统方程: (9) 根据建立的政府碳规制与重污染企业碳减排策略的演化博弈模型,建立系统动力学模型如图2所示。 图2 政府与重污染企业演化博弈系统动力学模型示意图 根据上述政府碳规制和重污染企业碳减排策略的复制动态方程可知,政府碳规制策略的复制动态方程如式(10)所示: (10) (11) 2) 当C-βQ-W-P<0时,即政府积极规制的总成本小于碳税、政府信誉损失以及政府惩罚之和时,又可分为如下2种情况。 根据上述演化博弈情况,x的动态变化趋势及稳定性如图3所示。 图3 政府碳规制策略行为复制动态相位 根据式(9)可知,重污染企业碳减排策略的复制动态方程如式(12)所示: (12) (13) 根据上述演化博弈变化情况,y的动态趋势及稳定性如图4所示。 图4 重污染企业碳减排策略行为复制动态相位 3.3 政府与重污染企业混合演化博弈稳定性分析 根据前文所述,在不同的初始条件下政府与重污染企业分别存在3种演化稳定策略。当C-βQ-W-P<0时,即政府积极规制的总成本小于碳税、政府信誉损失与政府惩罚之和时,政府有x=1和x=0两种演化博弈稳定策略。当αI+(β+γ)(Q-Q′)+P>R+I-S-R′>0时,重污染企业有y=1和y=0两种演化博弈稳定策略。 重点讨论C-βQ-W-P<0、αI+(β+γ)·(Q-Q′)+P>R+I-S-R′>0条件下的政府和重污染企业混合策略的稳定性。 令F(x)=0,f(y)=0,当 (14) 根据Friedman的观点可知,通过系统雅克比矩阵的局部稳定性可以得出演化博弈均衡点的稳定性[19]。由政府和重污染企业演化博弈复制动态方程得到其相应的雅克比矩阵如式(15)所示: (15) 矩阵J行列式为: detJ=(1-2x){y[-αI-β(Q-Q′)-W-P]+(βQ+W+P-C)}(1-2y){x[αI+ (β+γ)(Q-Q′)+P]+(R′-R-I+S)}+x(1-x)[-αI-β(Q-Q′)- W-P]y(1-y)[αI+(β+γ)(Q-Q′)+P] (16) 矩阵J的迹为: trJ=(1-2x){y[-αI-β(Q-Q′)-W-P]+(βQ+W+P-C)}+ (1-2y){x[αI+(β+γ)(Q-Q′)+P]+(R′-R-I+S)} (17) 雅克比矩阵反映一个微分方程与给定点的最优线性逼近,通过分析系统的雅克比矩阵,可以判断系统稳定点是否为ESS,当满足detJ>0,且trJ<0时,系统处于稳定状态。对上述均衡点进行稳定性分析,结果如表3所示。 表3 复制动态演化系统稳定策略 由以上分析可知,该博弈模型有一个中心点和4个鞍点,分别是E1(0,0)、E2(0,1)、E3(1,0)、E4(1,1)及E5(x*,y*),点(x*,y*)对应的特征根λ1,λ2为一对纯虚根。(x*,y*)是稳定的平衡点,但不是渐进稳定的;系统演化轨迹是绕着中心点的闭轨线环,闭环线没有通过中心E5(x*,y*),不存在极限环。 表4 政府与重污染企博弈参数值设置 图5 不同初始值下重污染企业积极碳减排策略的概率演化曲线(初始值x=x*) 从图5中可以看出,当政府碳规制概率为Nash均衡值(x=x*)时,重污染企业采取碳减排的概率不存在稳定状态,呈现周期性波动,系统无法稳定到中心点(x*,y*),即(x*,y*)不是系统的演化稳定策略。重污染企业碳减排概率y的初始值不同,波动的幅度与周期性也有所不同,企业一方Nash均衡策略点为y=0.45,企业采取积极碳减排策略的概率值离均衡点越近,波动幅度越大,波动周期越小。 2) 当0 由图6、7可以看出,在这2种情况下,政府与重污染企业这在博弈过程中呈现出一种周期行为模式,政府碳规制和重污染企业碳减排行为不存在演化稳定策略。 图6 政府积极碳规制演化博弈概率波动曲线 图7 重污染企业积极碳减排演化博弈概率波动曲线 政府的碳规制策略主要有4种:碳惩罚、碳交易、碳税与碳补贴策略,这4种策略是对重污染企业碳减排行为的奖惩策略。在这4种静态碳规制策略的作用下,重污染企业选择积极碳减排策略与消极碳减排策略的概率波动曲线如图5、7所示,呈现周期性震荡,并未稳定在一个固定值。因此,为了使重污染企业采取积极碳减排的概率稳定在一个固定值,并为其提供理论指导,采用动态碳规制策略对上述静态碳规制策略做优化。政府动态碳规制策略存在4种方案:动态碳惩罚策略、动态碳税策略、动态碳交易策略与动态碳补贴策略。运用系统动力学的方法,在控制其他碳规制策略为静态策略时,对这4种动态策略逐一进行仿真模拟,观察重污染企业积极碳减排概率的波动情况。 4.1.1动态惩罚策略 若重污染企业不采取积极的碳减排策略,假设其造成的环境破坏程度(如碳排放过度、温室效应)与其不采取积极碳减排策略的概率成正比,则可用1-y表示重污染企业碳排放对环境的破坏程度;当重污染企业采取消极的碳减排策略,政府采取积极碳规制策略时,假设重污染企业受到的惩罚由原来的P变成f(y)=(1-y)Pm,其中Pm代表惩罚的最高力度,且Pm>I。 4.1.2动态碳补贴策略 政府采取碳补贴政策是为了鼓励重污染企业积极地进行碳减排技术创新,因此对于碳减排意愿较低的重污染企业,政府有很强的意愿对其实施激励举措,促使其加大碳减排技术创新投入,因此对这类企业,政府的补贴比例较高。相反,对于采取碳减排意愿比较强烈的重污染企业,政府需要适当减弱采取的激励措施,因此对于这类企业的补贴比例较低。综上所述,可假设政府对重污染企业碳减排技术创新投入的补贴比例与企业采取积极碳减排策略概率成反比,即当重污染企业采取积极的碳减排策略,政府实施积极的碳规制策略时,假设重污染企业得到的补贴比例由原来的α变为h(y)=(1-y)αm,其中αm代表碳补贴上限且0<αm<1。 4.1.3动态碳交易策略 政府采取碳市场交易政策是为了通过市场调节手段控制重污染企业碳排放量,在进行总体控制的前提下,允许企业进行碳排放权的交易,以市场为基础对环境经济进行刺激。政府根据企业性质,分配给重污染企业一定的碳配额,若企业实际的CO2排量超过给定的碳配额,则企业需购买超出碳配额部分的碳排放权;若企业实际CO2排量未达到碳配额,则可以出售剩余的碳排放权,以获得经济利益的回报。其购买成本与收益大小取决于超出量与碳市场碳交易价格。在企业碳排放量既定的前提下,企业获得碳减排收益与碳惩罚成本的关键取决于碳交易价格。因此对不积极采取碳减排策略的企业,政府可通过增加其碳价成本即较高的碳价,促使其实施低碳减排。对于积极碳减排的企业,通过增加碳价促使其碳减排的必要性减弱,因此给予这类企业较低的碳交易价格。综上所述,政府制定的碳交易市场价格与重污染企业积极碳减排的概率成反比,即重污染企业积极碳减排时,其碳交易价格将由原来的γ变为g(y)=(1-y)γm,其中γm代表碳价上限。 4.1.4动态碳税策略 政府采取的碳税政策是对企业碳排放量进行征税,政府的碳税政策本着惩罚高碳排企业,激励企业积极实施碳减排策略的目的。对于重污染企业这种碳排放高的企业征收较高的碳税,对于积极实施碳减排政策的企业实施低碳税甚至零碳税政策。因此政府碳税税率与重污染企业积极碳减排的概率成反比,即重污染企业采取积极的碳减排策略时,其受到的碳补贴价格由原来的β变为q(y)=(1-y)βm,其中βm代表碳价上限。 4.2.1动态碳惩罚策略稳定性分析 政府动态的碳规制策略改变了政府与重污染企业博弈的收益矩阵,对动态碳规制策略混合矩阵进行稳定性分析。首先进行动态碳惩罚策略的稳定性分析,将f(y)=(1-y)pm代替(9)中的P,得到碳惩罚动态系统的复制动态方程如式(18)所示。 (18) (19) 由上式可知0 (20) 令: a=R+I-S-R′ b=αI+(β+γ)(Q-Q)+(1-y*)Pm c=C-βQ-W-(1-y*)Pm d=-αI-β(Q-Q′)-W-(1-y*)Pm (21) 其中,A′、B′与C′分别为: (22) 4.2.2动态碳补贴策略稳定性分析 将h(y)=(1-y)αm代替(9)中的α,得到碳惩罚动态系统的复制动态方程如式(23)所示: (23) (24) 令x**与y**满足0 (25) 对式(25)化简整理可得: (26) (27) 其中A″、B″与C″如式(28)(29)与(30)所示: (28) (29) (30) (31) 由上述4种动态碳规制策略的系统稳定性分析可知,政府与重污染企业双方策略的演化博弈轨迹最终呈现螺旋轨线稳定于各自焦点。因此,为了证实上述理论分析,使用VENSIM软件进行动态碳规制策略的系统动力学模型仿真,模拟分析在政府动态碳规制策略作用下,重污染企业实施碳减排策略的演化博弈过程。设置政府与重污染企业采取积极措施的概率初始值分别为x=0.2,y=0.2。在4种动态碳规制作用下,政府与重污染企业双方策略演化博弈轨迹分别如图8~11。 图8 动态碳惩罚下政府与重污染企业演化博弈轨线 图9 动态碳补贴下政府与重污染企业演化博弈轨线 图10 动态碳价下政府与重污染企业演化博弈轨线 图11 动态碳税下政府与重污染企业演化博弈轨线 从图8~11可以看出,在政府实施动态碳规制策略的条件下,博弈双方的演化博弈轨线最终都螺旋的趋向于各自的稳定焦点,从而证实了上述系统稳定性理论分析,即政府实施动态碳规制策略有利于博弈双方达到系统的稳定均衡点。 为了进一步探讨在不同动态碳规制作用下重污染企业积极碳减排的概率变化,更好地为政府制定科学的碳规制政策,为重污染企业提供科学的碳减排策略建议,通过VENSIM软件模拟在动态碳规制作用下政府与重污染企业演化博弈过程,结果如图12、13所示。 图12 动态碳规制作用下的政府积极碳规制概率演化曲线(初始值:x=0.2,y=0.2) 图13 动态碳规制作用下重污染企业在积极碳减排概率的演化曲线(初始值:x=0.2,y=0.2) 如图12、13所示:在动态碳规制策略的条件下,政府实施碳规制策略与重污染企业实施碳减排策略的概率随着时间和博弈次数的增加而趋于稳定。如图12所示,在政府实施动态碳规制策略的作用下,不同的碳规制政策最终稳定的均衡点不同,如在实施动态碳惩罚策略下,重污染企业的积极碳减排概率达到稳定均衡点值为y=0.169;在动态碳价策略下,企业达到的稳定均衡点概率值y=0.363 6;在动态碳税策略下,企业达到稳定均衡点概率值y=0.238;在动态碳补贴策略下,企业达到稳定均衡点概率值y=0.238。从结果可以看出,在动态碳惩罚策略作用下,企业选择积极碳减排措施的概率值低于初始值,在动态碳价、动态碳税与动态碳补贴的作用下,重污染企业选择积极碳减排措施的概率最终稳定值高于初始值,且结果表现出动态碳补贴优于动态碳价优于动态碳税。因此,为了促进重污染企业积极实施碳减排创新技术投资,政府在进行碳规制策略时,可考虑动态碳规制策略优于静态碳规制,动态补贴策略优先于动态碳价,动态碳价策略优先于动态碳税策略。 1) 政府与重污染企业存在以下3个演化稳定策略:① 当C-βQ-W-P>0时,x=0是演化稳定性策略,其中C为当政府采取积极碳规制策略时的总成本,βQ为政府积极碳规制下,企业消极碳减排时政府征收的碳税,W为政府消极碳规制下企业消极碳减排时的政府信誉损失,P为政府积极碳规制下企业消极碳减排时受到的惩罚,即当总成本大于其余三者之和时,作为有限理性的政府最终会选择消极的碳规制策略,并且不依赖于重污染企业的选择策略。② 当R+I-S-R′<0时,则y=1是演化稳定策略点,其中R′表示企业采取积极碳减排策略时的收益,R表示企业采取消极碳减排策略时的收益,I为企业采取积极碳减排策略时的创新技术投入,S表示采取消极碳减排策略时的机会损失,即当企业采取积极碳减排策略时的收益与消极碳减排时的机会损失之和大于其余两者之和时,作为有限理性的重污染企业最终会选择积极的碳减排策略,且不依赖于政府策略的选择。③ 当R+I-S-R′>αI+(β+γ)·(Q-Q′)+P>0时,则y=0是演化稳定策略,其中αI为政府积极碳规制下,企业积极碳减排时享受到的补贴,(β+γ)(Q-Q′)表示碳税税率与碳价之和与重污染企业消极碳减排和积极碳减排时碳排放量之差的乘积,即表示当重污染企业消极碳减排时的收益R与积极碳减排时的创新投入I之和大于企业消极碳减排时的机会损失S与积极碳减排时的收益R′等五者之和时,有限理性的重污染企业最终会选择消极的碳减排策略,不依赖于政府策略的选择。 3) 当政府实施动态碳规制策略,即动态惩罚、动态碳税、动态碳价与动态碳补贴时,系统均存在4个鞍点与一个稳定点,且演化轨迹均以螺旋式趋向于稳定焦点,这表明政府选择实施积极碳规制策略的概率随着时间的增加逐渐收敛,最终稳定在混合策略的Nash均衡点,即说明政府对重污染企业进行动态碳规制策略时,政府与重污染企业的博弈可达到均衡。通过系统仿真分析,政府采取动态碳规制策略时,重污染企业选择积极碳减排措施的概率最终将大于初始值,且在结果表现出的优劣关系中,动态碳补贴优于动态碳价,动态碳价优于动态碳税。这将为政府在制定相关碳减排策略时提供参考,从而制定出更有效的市场监管策略,且重污染企业也可根据政府制定的相关碳规制政策调整自己的碳减排策略,最终在保证效益的同时减少碳排放,促进环境与社会经济的协调发展。

2.2 演化博弈模型建立
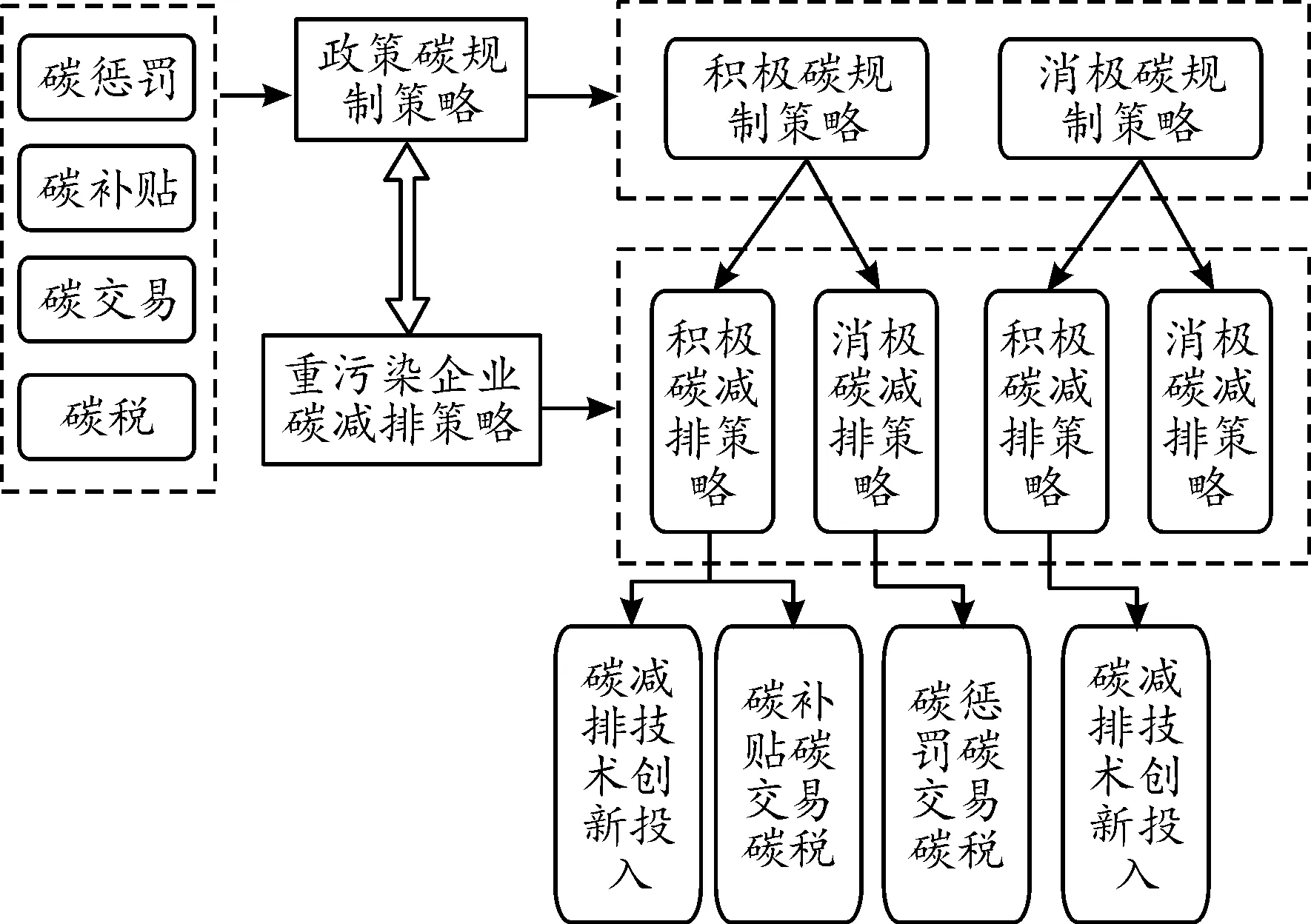



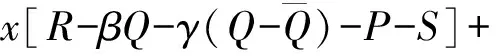
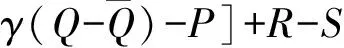

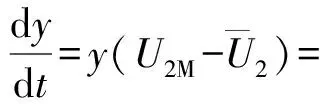

2.3 演化博弈系统动力学模型

3 政府与重污染企业演化博弈模型稳定性分析
3.1 政府单方策略稳定性分析


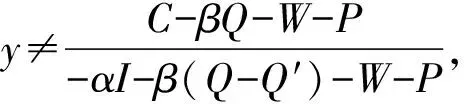
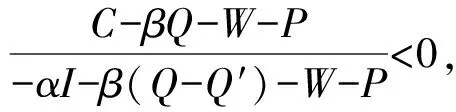

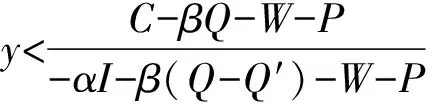

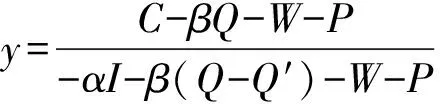
3.2 重污染企业单方策略稳定性分析
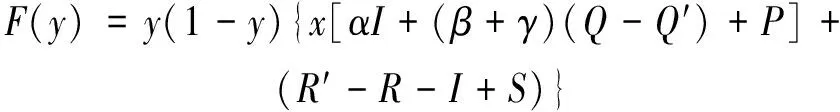




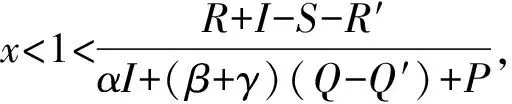





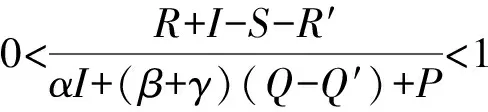

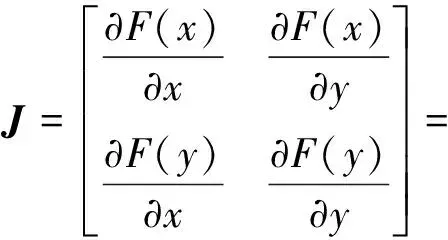
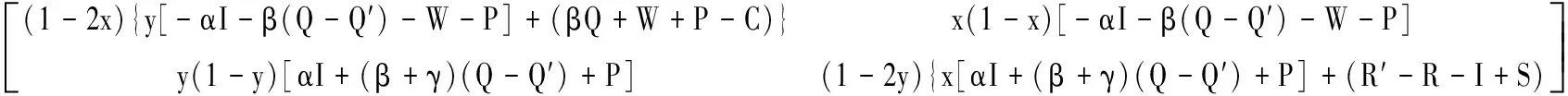

3.4 仿真模拟





4 不同策略方案仿真模拟
4.1 动态碳规制策略
4.2 政府动态碳规制策略的系统稳定性分析


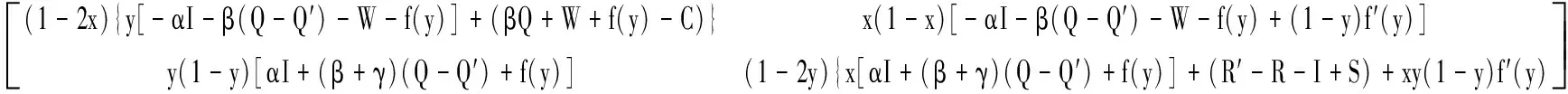

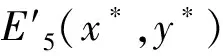



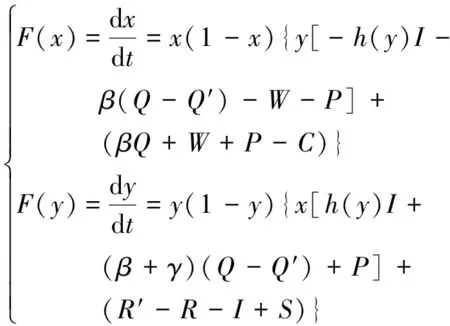


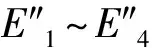
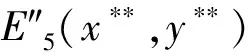



4.3 动态碳规制策略下的系统仿真分析






5 结论


