计及联合效益的分布式光伏并网接纳能力研究

喻 婷，曾成碧

(1.四川大学，成都 610065；2.国网四川省电力公司眉山供电公司，四川 眉山 620000)

随着经济的快速发展，我国对能源的需求量在加速增长。由于传统能源结构会对环境造成严重破坏，新能源替代传统能源成为大势所趋。在各种新能源中，太阳能具有清洁、安全、分布广泛、永不枯竭的优点，光伏发电在各种发电方式中所占比重也越来越大。但光伏发电过程中，光伏出力波动不稳定，随着环境变化，具有随机间歇等特点，对电网的安全稳定和控制调度等都是极大的考验，对光电并网产生的经济效益也有一定限制。

为了提升配电网中光伏的接纳容量，国内外相关专家进行了大量研究[1-3]。刘波等[4]通过功率变化引起电压波动来对地区配电网接纳光伏容量进行分析，发现平均功率因数越小，允许接纳能力越小，功率波动越大，对电网中的电压质量影响越大。武兆亮等[5]建立了分布式光伏最大准入容量模型，选取粒子群算法作为优化算法，对IEEE33节点配电系统进行模拟计算，考虑电压约束，得出最大准入容量为8.8MW。周良学等[6]针对光伏智能逆变器电压/无功控制，基于OpenDSS仿真平台进行实例分析，发现光伏逆变器/无功控制可有效改善电压和光伏接入容量。孙强等[7]研究分布式光伏出力同负荷相关性对接入容量的影响，采用模拟退火算法和前推回代算法进行研究，发现其接纳能力和负荷情况有很大关系。刘琳等[8]在研究中发现，配电网中适当接入分布式光伏系统能减少网络损耗，但当光伏并入电网的容量高于负荷容量的2倍时，分布式光伏接入电网反而会增加配电网的网络损耗。

针对分布式光伏接纳容量的研究重点考虑满足电网安全、稳定运行约束(或者电流约束和电压约束等)时的最大光伏接纳容量，未考虑光伏发电带来的经济效益。本文中考虑电网安全、稳定运行时，满足功率、电压和电流约束，使光电站和配电网的联合效益(包含环境效益)最大化的分布式光伏最佳接纳能力。采用鸡群算法对基于博弈论的配电网分布式光伏最优接纳能力的模型进行求解和分析。鸡群算法具有很强的收敛性，能精确求解复杂多目标优化问题。将分布式光伏接入IEEE 33节点配电网系统。由于24 h负荷具有正态变化，故各个节点在不同时间点的负荷不同。求解不同时间段的联合效益最大时的光伏最佳接纳能力。

1 基于博弈论的配电网分布式光伏最佳接纳能力

1.1 光电站和电网的博弈模型

光电站的初期投资成本较大。当光电站投入的容量越大时，光电站发电效益和环境效益越大，整体收益越好，所以光伏电站应尽可能提高输出容量以提高收益。光伏出力波动和间歇会给配电网带来冲击，影响配电网的稳定性和安全性，故电网在保证安全稳定运行的前提下会限制接纳光伏容量并网，以尽可能提高自身的经济效益。光电站和配电网寻求自身最大效益时，两者间会产生博弈问题。本文中，讨论前提是国家调控政策可以调整控制光电站和电网之间的收益。如果光电站和电网选择合作联盟，最优策略是联盟总收益最大，经过收益的再次分配，使两者的收益大于其他策略产生的收益；当光电站和电网选择合作，结成联盟时，配电网才能在满足系统负荷增长需求的同时满足一定的经济性。光电站和电网的博弈模型为：

1) 参与人：光电站和配电网，用W和G表示。

2) 参与人策略：在二者的博弈中，W和G的博弈策略都是接纳光伏的容量，记为PW。由于地理位置、海拔高度、温度、光照强度等外界条件的影响，光电站的建设规模会受到限制，因此策变量有上限和下限，即策略空间SW。

PW∈{SW=[PWMIN,PWMAX]}

(1)

式中：PWMIN为光电站容量下限；PWMAX为光电站容量上限。

3) 参与人收益：W和G的收益等于收入减去费用，记为IW和IG。

4) 均衡策略：PW*是博弈模型的最优均衡策略，能使总效益达到最高，满足式(2)：

IW(PW*)+IG(PW*)≥IW(PW)+IG(PW)

PW∈SW

(2)

其中：光电站和电网合作博弈的最终均衡策略是获得使联合系统经济效益达到最大的分布式光伏并网容量。

1.2 目标函数

分布式光伏发电并入电网后，光电站和电网之间的均衡策略是采取合作博弈，获得使联合系统的经济利益(环境效益)最大的分布式光伏接纳能力。常见的分布式光伏接纳容量分析重在考虑电网安全运行约束，包括电流约束和电压约束等。本文中定量分析光伏系统接入电网对光电站和配电网的成本和环境效益，以联合效益(含环境效益)最大化为目标，考虑电网安全运行约束，建立了分布式光伏发电最佳接纳模型。

目标函数以联合效益(含环境效益)最大化为目标：

CWj+CGOj+CGAj]

(3)

其中：V为联合系统净收益；N为光伏并网节点；IWC为光电站每年得到的国家补偿收益；IGS为光伏发电的环境收益；IGC为电网年获得的补偿收益；IEM为光电站每年出售电能获得的收益；CWC为光电站初期建设投资费用；CGj为光伏接网费用；CW为光电站每年的运行维护费用；CGA为电网每年的辅助服务成本；CGO为电网每年的运行维护费用；i为银行利率；TW为光电站的寿命年限；1-(1+i)-TW为等效年值系数；T为新修线路的运行年限。

1.3 约束条件

1) 盈利能力约束：V>0

2) 光电站和配电网的联合系统净效益等于总效益减去总成本，当净效益为0时，收益与成本相等，称之为盈亏平衡。只有当联合系统的净效益为正数时，策略可以被采纳。

3) 系统有功平衡约束为

(4)

式中：M为常规发电机组的台数；N为光电站数；PG.i为常规机组的有功出力；PW.i为分布式光伏并网容量；Pload为有功负荷；ΔPLOSS为有功网损。

4) 光伏发电容量上限约束为

Si≤Smaxi=1,2,3,4,…,n

(5)

式中：Si为第i个节点接入电网的光伏容量；Smax为节点接入配电网的光伏容量上限。

5) 节点电压约束为

Umin≤Ui≤Umax

(6)

式中：Ui为节点i的电压；Umin为节点电压约束的最低电压；Umax为节点电压约束的最高电压。

1.4 算法流程

1.4.1鸡群算法

常见的群智能优化算法如粒子群算法、蚁群算法等，选取的初始点大部分为均匀分布的随机值。在算法的迭代过程中，每个个体独立且没有相互约束，对目标函数没有过多要求，应用范围广，可解决复杂的优化问题。

鸡群算法(CSO)是一种基于鸡群搜索行为提出的新型全局优化算法，通过对鸡群的种类划分建立等级制度进行寻优。鸡群中存在公鸡、母鸡和小鸡，他们各自的寻优搜索策略不同，鸡与鸡之间也存在竞争和学习关系。在迭代中，每只鸡的适应度会发生变化，并建立新的等级关系。相比其他群智能优化算法，鸡群算法具有控制参数少、稳定性高等优点，在求解复杂多目标优化问题时更加精确和稳定。实验结果表明，鸡群优化算法在解决优化问题时，其准确性、鲁棒性均表现良好，性能优于粒子群算法。

鸡群中的每个个体对应求解的优化问题中的解。不同的鸡群，个体位置的更新公式也不同。公鸡是鸡群中适应度最佳的个体，它找寻食物的范围更广，相应的位置更新表示为

(7)

式中：Randn(0,σ2)产生均值为0、标准差为σ2的正态分布的随机数；fk表示第k只公鸡的目标函数值；ε表示一个比较小的数。

母鸡的位置更新表示为

(8)

其中：rand函数产生[0，1]范围均匀分布的随机数；r1为第i只母鸡所在群中的公鸡；r2为所有种群中公鸡和母鸡中的任意一个个体，且r1不等于r2。

小鸡的位置更新表示为

Xij(t+1)=Xij(t)+F×[Xmj(t)-Xij(t)]

(9)

其中：m为第i只小鸡对应的母鸡；F(F∈[0,2]) 为小鸡跟随母鸡的行走步长，即跟随系数。

鸡群算法基本流程见图1。

图1 鸡群算法基本流程框图

1.4.2罚函数

针对多约束优化问题，提出了一种结合罚函数的改进鸡群优化算法，借助罚函数将约束优化问题转化成鸡群优化算法可以求解的无约束问题。

罚函数法是解决约束优化问题的一种关键方法，它通过设立惩罚项将包含多种约束的目标函数求解问题转化成求解无约束极小化问题，是一种制约函数法。遵循鸡群进化机制，根据鸡群中可行解的躲闪、个体约束违反程度对鸡群里个体的适应度做出适当修正：

Fi(x)=di(x)+pi(x)

(10)

式中：Fi(x)为个体x目标i的修正适应值。其中：di(x)为个体x对目标i的距离值，表示个体离可行解的距离；pi(x)为目标的惩罚值，表示个体可行性的惩罚因子。

1.4.3分布式光伏接纳能力优化流程

步骤1初始化每个光电站的装机容量，采集当地负荷消纳能力、常规机组装机容量，得出各光电站出力情况。

步骤2进行光电站小时发电量的计算，获得只和光伏发电量有关的目标函数。光电站的成本和效益包括光电站投资建设成本、运行维护费用、国家给予的补贴效益；电网方面的成本和效益包含光伏接网费用、运行维护成本、出售光电获得的收益、国家给予的补偿收益和光伏发电带来的环境效益。

步骤3进行电力系统33节点潮流计算。检查校验结果是否满足电压电流和功率约束条件，若满足，累积该时段联合系统的成本效益分子；否则，运用罚函数做校正控制，满足电网安全稳定运行约束后确定电力系统新的运行点，确定各节点的光伏接入容量，并输出该时段的成本效益分子。

步骤4用鸡群算法和罚函数优化最终得到的联合净收益最大时的分布式光伏最佳接纳容量和最大效益，即为光伏最佳接纳方案。

步骤5选取1天的几个时间段，重复步骤1～4，得到不同时间段的最大光伏出力和经济效益。

分布式光伏接纳能力优化流程见图2。

2 算例结果分析

2.1 算例分析

采用IEEE33节点配电网系统，拓扑结构包含32条支路，5个联络开关，1个电源。负荷参数为原模型参数，配电网的网络总负荷为5 086.26+j2547.32 kVA。在除平衡节点外的32个节点分别并入光伏，首端基准电压为12.66 kV，三相功率基准取10 MVA，Uimin=0.93UN，Uimax=1.07UN，光伏发电容量上限为Spv.max=1 000 kW；电流约束上限为300 A。鸡群算法种群数pop=10，最大迭代次数M=100。

图2 分布式光伏接纳能力优化流程框图

在鸡群算法中，鸡群规模通常取决于经验，鸡群数量过少不利于求解最优解，鸡群数量过多则会增加算法成本。Meng等[14]将种群数量设定为100，本文中分别将种群数5、50、100、200、500代入Matlab进行计算后发现，种群数达到100后，目标数值精度差距较小。

对于目标函数最大联合经济效益，光电站、电网、环境相关成本和效益的计算如下：光伏电站的成本主要为初期建设成本(8.2元/W)、运行维护费用(196万/年，224元/时)；光伏电站效益分为3部分，一部分是国家给予的新能源补贴，补贴电价为0.42元/kW·h；一部分是节省的用电费用，电价为1元/kW·h；一部分是多余的电量上网费用，电价是0.8元/kW·h。配电网成本主要考虑收购光电运行成本，为0.086元/kW·h；电网购光电成本 为0.8元/kW·h；配电网的效益主要包含电网售电收益，约为1元/kW·h；国家给予补贴 为0.02元/kW·h。另外，还需考虑环境效益，环境效益表达式为

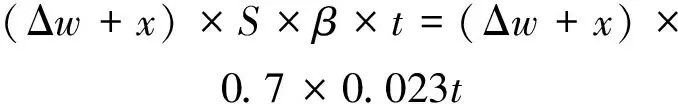
(11)

其中：Δw为减少(或者增加)的网损；x为全部接入的光伏容量。

综上，将总的效益减去成本可得到系统总效益和目标函数。目标函数表示为

(12)

其中：x为光伏接入总量；z为接入光伏后的网损增减量。

2.2 加入光伏后潮流分析

在配电网中加入光伏后，用Matlab和鸡群算法计算系统总效益(包含环境效益)最大时分布光伏的最佳接纳能力，并获得各个节点在加入光伏后的电压增减情况和网损情况。在除平衡节点外的其余32个节点并入光伏，联合效益在鸡群算法中的迭代进化过程曲线见图3，联合效益迭代进化过程中获得的分布式光伏节点安装容量见表1。

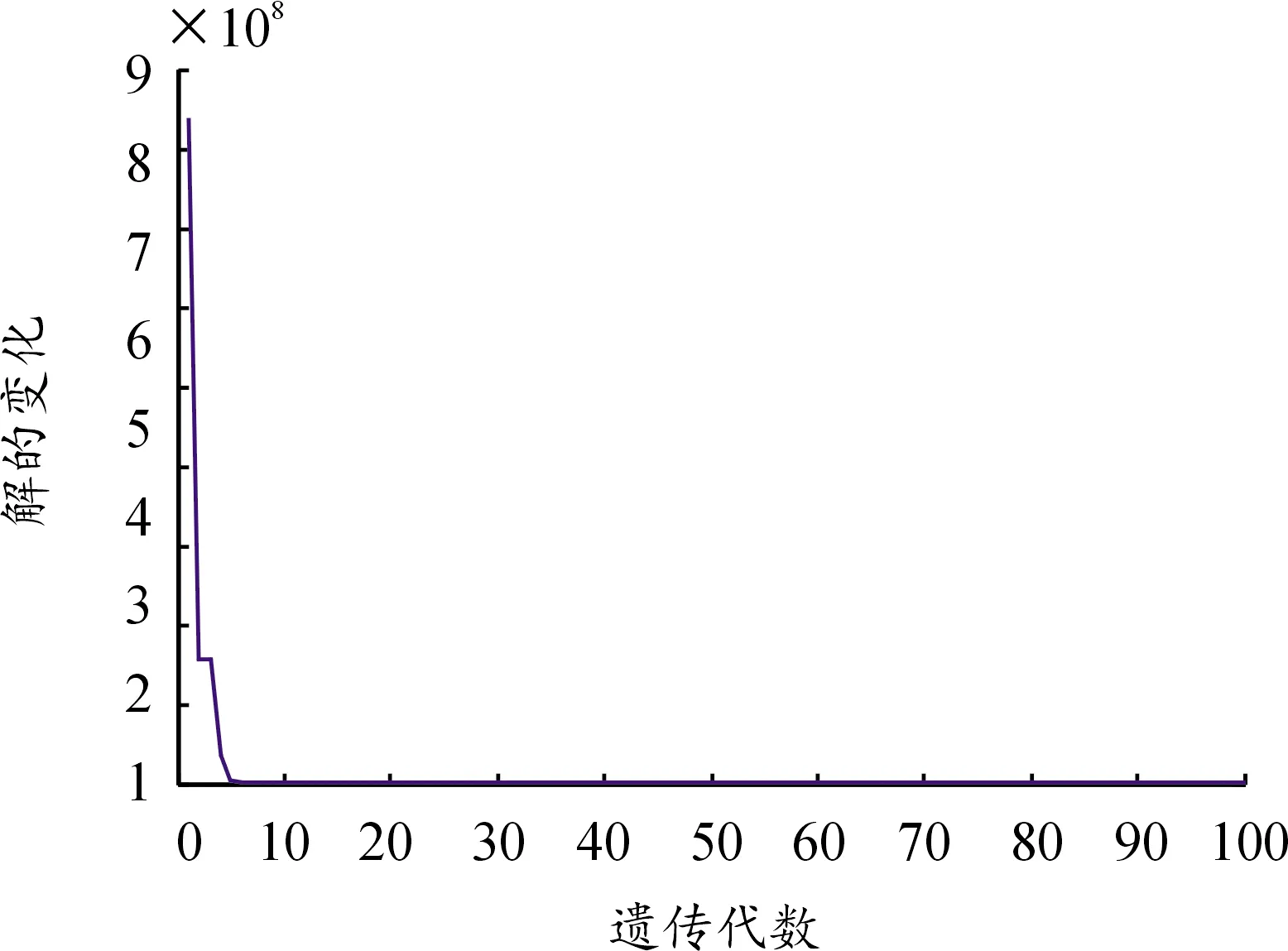
图3 联合效益迭代进化过程曲线

表1 分布式光伏节点安装容量

节点数光伏容量/kW电压UN12253.8620.971317.239 250.964140.000 347 60.962150.997 6270.96116962.162 70.9591700.95818120.008 80.95719984.739 31.03720801.413 61.03321381.814 31.0322240.880 171.032

节点数光伏容量/kW电压UN23115.855 51.0224189.672 11.012250.000 41.0112616.383 20.992788.967 70.98828124.561 70.9772938.376 010.96930135.096 60.965310.000 70.961322.066 340.9613313.249 50.96

由表1的数据得知，分布式光伏接入总量为5.844 MW，最大光伏量接入节点为19节点，984.739 3 kW，接入光伏后的网损为0.185 2 MW，单位小时的联合效益(包含环境效益)为 23 713.259 9元。

2.3 加入光伏后考虑时序的潮流分析

加入分布式光伏后，由表1的数据可知：配电网系统的最低节点电压和平均电压都在一定程度上有所提高。最低电压由0.913 1UN提升到0.957UN；平均电压由原来的0.948 5UN提升到0.990 7UN；系统的有功网损从原来的0.206 7 MW降至0.185 2 MW。加入分布式光伏后，原有电压不合格节点的电压值均在(0.93～1.07)UN范围之内，满足电压偏差的要求，支路电流满足电流约束。

选取一天24 h中具有代表性的时间段，研究不同时间段联合效益最大时的光伏最佳接入容量。由于1 d内负荷变化服从正态分布，各节点在不同时间的负荷不同(见表2)，选取6∶00、8∶00、10∶00、12∶00、14∶00、18∶00时间段来研究光伏出力和系统效益。各个节点在各时段的负荷数据见表2。

各节点在 1 d内不同时段的负荷是不同的，接入的光伏容量也不同。将每个时段的负荷量在Matlab中重新计算，得到总的光伏出力和环境效益(见表3)。

表2 各时间段各节点负荷

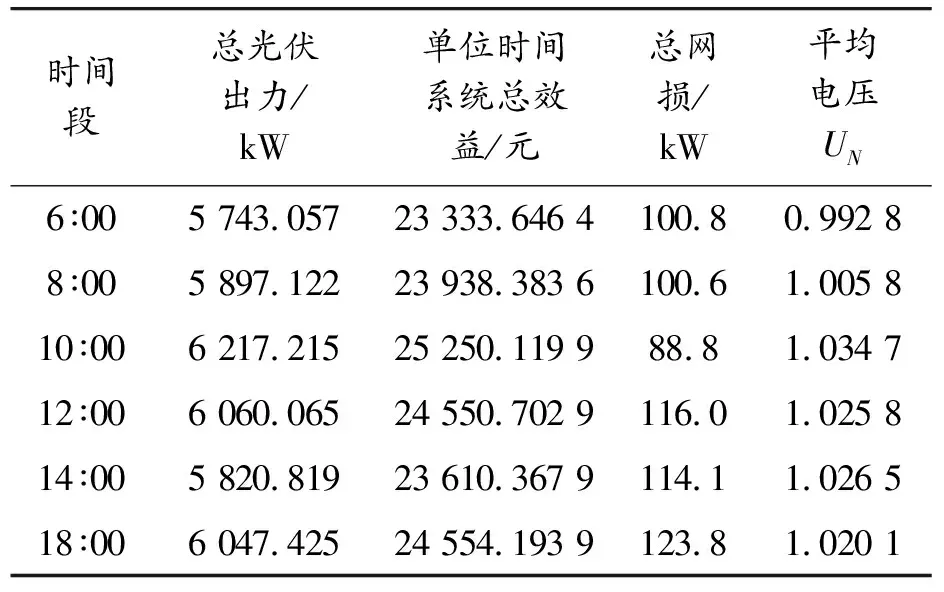
表3 不同时段的光伏出力、总效益、网损和电压

由表3可知，随着配电网中负荷容量的增加，各节点的光伏接入容量也随之增加，单位时间内的系统总效益随着光伏总接纳容量的增加而增加，且并入电网的光伏容量越大，提升电压越高,平均电压也会提高。网损随着并入光伏容量的不同而不同，在10∶00时刻，总光伏出力最大，为6 217.215 7 kW；总网损最少，为88.8 kW，系统总效益最高，为25 250.119 9元。

通过对不同时间段光伏最佳能力接纳模型的计算分析，得到节点负荷变化下满足最大经济效益的动态时序最佳光伏出力。相较传统的研究方法，本研究重点考虑光伏并网的经济性，在满足安全约束的情况下，以获得最大经济效益为目标得到最佳光伏接纳能力。

3 传统的光伏最佳接纳能力

将光伏建设初期成本调整为10元/W，利用最佳接纳模型进行计算，获得不同节点光伏最大接纳容量，如图4所示。联合效益最大时，分布式光伏接入总量为5.324 MW，网损为0.152 8 MW，系统单位小时的总效益(包含环境效益)为20 588.324 1元。

图4 系统效益最大时各节点光伏接纳容量

传统的光伏最佳接纳模型[7]在保证节点电压和线路电流不越线的条件下以净收益为目标，采用布谷鸟算法得到光伏最大接入容量和经济效益。当光伏建设成本为10元/W时，采用IEEE123节点算例，得到各节点光伏接入容量(见图5)，联合效益最大时，分布式光伏接入总量为2.990 MW，最大日均净收益为5 364.1元。

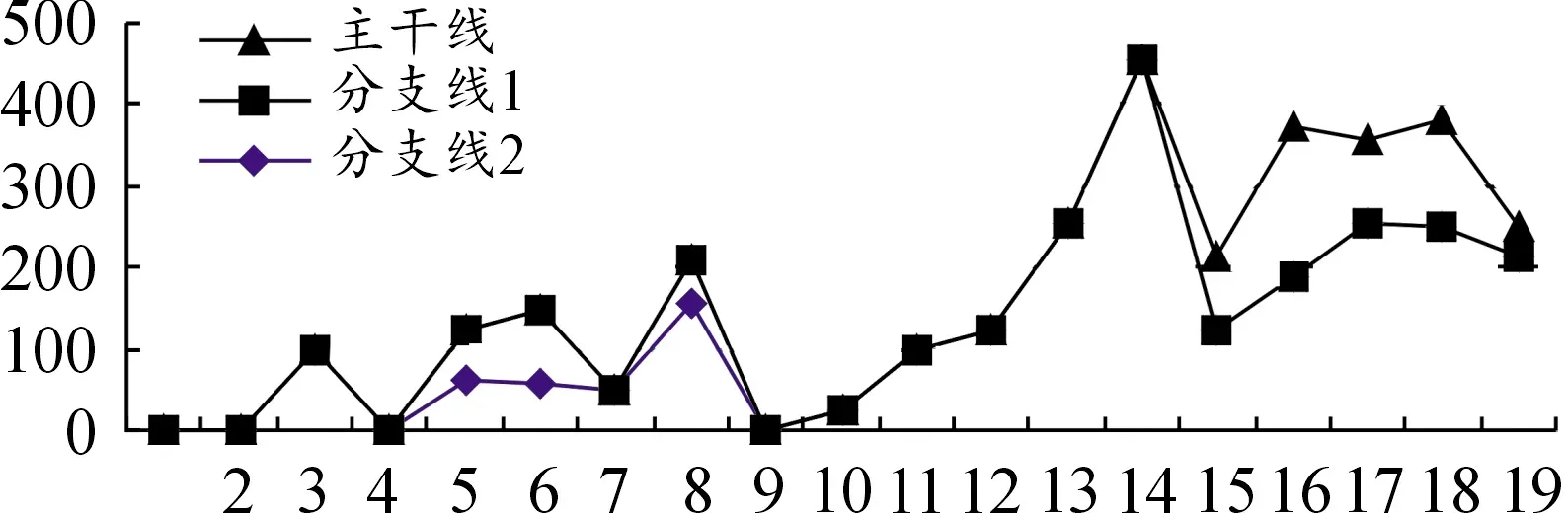
图5 系统效益最大时各节点光伏接纳容量

由图4、5可知，本文中建立的模型和方法与传统的模型都能在满足系统安全稳定约束的前提下得到最大的联合经济效益。本文中采取合作博弈的形式，利用鸡群算法进行优化，得到的最大经济效益优于传统模型，可同时得到光伏接入量不同时的网损量。

4 结论

建立了基于博弈论的配电网分布式光伏最佳接纳模型，并构造鸡群算法对不同时间段光伏最佳接纳能力进行计算和分析，得出配电网光伏最佳接纳能力方案和各节点光伏并网与电压、网损、总效益之间的关系。相比其他方法，本文中提出的基于博弈论的配电网分布式光伏最佳接纳模型除考虑光伏并网的安全约束外，还考虑光伏发电的经济效益，最终在有效提高配电网光伏最佳容量的同时，得到最大的经济效益。与传统方法对比发现，新方法的经济效益更高，采用的鸡群算法具有很强的收敛性，能较为精确地求解复杂多目标优化问题，性能优于传统的多目标算法，能更加有效地避免陷入局部最优。

下一步工作中，将使用实际电网进一步验证和研究分布式光伏最佳接纳能力模型的作用。