考虑变分模态分解残差量的电力负荷预测研究

张 莲，李 涛，宫 宇，杨洪杰，张尚德，贾 浩

(1.重庆市能源互联网工程技术研究中心， 重庆 400054; 2.重庆理工大学 电气与电子工程学院， 重庆 400054)

随着我国社会和经济的发展，电力市场化改革成为必然的趋势和要求，节能减排，实现碳达峰、碳中和是国家的重要目标。在这样的背景下，提高电力负荷预测的精度对于电力供需平衡、电力系统稳定、合理安排发电计划、减少不必要的能源消耗有着重要意义[1-2]。

相关研究者对电力负荷预测做了大量研究，提出了多种预测方法，例如自回归积分滑动平均法[3]、随机森林法[4-5]、支持向量机法[6]、神经网络法[7-11]等方法。随着深度学习的兴起与发展，各种具有深度学习功能的神经网络被广泛应用于电力负荷预测领域。张宇帆等[12]利用深度长短期记忆神经网络预测负荷功率，展示了深度LSTM神经网络在负荷数据特征学习方面的优越性。在以往的浅层神经网络中，只有隐藏层的神经元数量可以改变，而在LSTM神经网络中，可以改变网络的宽度和深度，因此在传统神经网络中的局部最优问题可以通过预训练的方式得到缓解。

对于具有高度随机、波动等特性的电力负荷序列，采用单一的预测方法往往不容易达到理想的预测精度。目前，各种组合预测方法在电力负荷预测领域得到了广泛应用，其中经验模态分解(EMD)算法可以有效地对原始负荷序列进行分解，达到平滑序列和非平滑序列互相分离的目的，然后再结合预测方法分别预测各个本征模态[13-14]分量。但是，EMD分解算法容易造成模态混叠，并生成虚假IMF分量，会对预测结果产生不利影响。文献[15]采用变分模态分解算法将负荷数据分解为具有不同特征的模态函数，可有效避免模态混叠，提升了信号的分析效果。

然而，以往采取VMD分解算法建立的组合预测模型直接抛弃了信息丰富的VMD分解后剩余残差量，这限制了模型的预测准确性。因此，提出了考虑VMD残差量的VMD-LSTM组合预测模型，改善VMD-LSTM组合模型的整体预测精度。

1 基本原理

1.1 VMD算法

2014年，Konstantin团队提出了一种自适应的数据处理算法——变分模态分解[16]，该算法通过迭代搜索变分模态的最优解，每个模态函数和中心频率不断更新，进而得到一系列具有一定带宽的模态函数。变分模态分解是对EMD算法的改进，可更好地避免模态混叠和端点效应等问题。

VMD算法将信号分解为预先定义的K个本征模态分量IMF，即IMF被重新定义为一个输入信号的模态函数uk(t)：

uk(t)=Ak(t)cos(φk(t))

(1)

式中：Ak(t)为瞬时幅值，Ak(t)≥0；φk(t)为相位。

φk(t)对t求1阶微分，得到uk(t)的瞬时频率ωk(t)：

(2)

具体的步骤如下：

步骤1对分解得到的每个uk(t)做HHT变换来计算其相关的解析信号及边际谱：

(3)

式中：δ(t)为单位脉冲函数。

步骤2 通过加入一个预估的中心频率e-jωkt，将各个uk(t)的频谱变换到其对应的基带；

(4)

步骤3 通过计算梯度的L2范数的平方来估计相应模态的带宽，构造出如下的约束变分问题：

(5)

式中：{uk}表示分解后的模态集合{u1,u2,…,uk}；{ωk}表示分解后的各模态对应的中心频率集合{ω1,ω2,…,ωk}； *为卷积符号；f(t)为输入信号。

步骤4 为了求解式(5)，引入二次惩罚项α和Lagrange乘数λ(t)，由此把问题转换成如下的无约束的变分问题：

(6)

(7)

(8)

(9)

式中：n为迭代次数。

步骤5 规定最大的迭代次数为N，使得正数n满足n≤N，存在任意ε>0，满足：

(10)

时，完成迭代，否则返回步骤4。然后对式(7)求解得到的K个IMF的频域结果进行反傅里叶变换，得到时域信号。

1.2 LSTM神经网络算法

在LSTM神经网络中有3个称之为“门”的控制结构，分别是遗忘门、输入门和输出门。其中输入门和遗忘门对LSTM神经网络能够记忆长期依赖关系至关重要。LSTM网络结构如图1所示[17]。

遗忘门决定了将丢弃多少过去的状态信息，其利用Sigmiod函数参考前面的结果和目前的内容：

ft=σ(Wf[ht-1,xt]+bf)

(11)

式中：ft为遗忘门的状态；ht-1表示上一次输出的结果；xt表示当前输入的信息；Wf和bf为遗忘门权重矩阵和偏置项；σ表示Sigmiod函数。当ft的值愈加接近于0，被遗忘的信息越多。

图1 LSTM网络结构示意图

输入门决定了记忆单元中将保存多少当前时刻网络的状态信息：

it=σ(Wi[ht-1,xt]+bi)

(12)

(13)

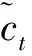
(14)

式中：ct为当前时刻的记忆单元；符号“∘”表示哈达玛乘。

最后，输出门决定了当前时刻内部状态中将输出多少信息给外部状态：

ot=σ(Wo[ht-1,xt]+bo)

(15)

式中：ot为输出门的状态；Wo和bo为输出门权重矩阵和偏置项。ot值越趋近于1，则当前时刻的外部状态ht就会从当前时刻的细胞状态ct中接收越多的信息。

2 建立模型

如前文所述，电力负荷序列通常具有非平滑、非线性和其他复杂的特性，使用单一的预测方法精度有限。VMD分解技术可以将复杂的信号分解成多个正则模态分量，降低原信号的复杂程度。因此，如果采取常规预测方法对VMD分解后的各个模态分量进行预测建模，那么预测精度会大幅度提高[18-19]。然而，以往的研究没有考虑VMD分解后残差量仍然含有的丰富信息，直接抛弃了残差量，从而降低了模型的预测精度。本文中提出在VMD分解的基础上充分考虑分解剩余残差量，结合LSTM神经网络的组合预测模型，其建模流程如图2所示。详细建模步骤如下：

步骤1对输入电力负荷序列数据进行归一化处理。

步骤2采用VMD算法分解归一化后的电力负荷序列，得到各个IMF，然后用分解前负荷序列数据减去各IMF数据之和，得到VMD分解剩余残差量。

步骤3对分解后的各IMF和残差量数据划分出合适的训练样本与测试样本，输入LSTM神经网络进行训练，得到各IMF和残差量的预测结果。

步骤4将各IMF及残差量的预测结果叠加并反归一化后得到最终预测结果。

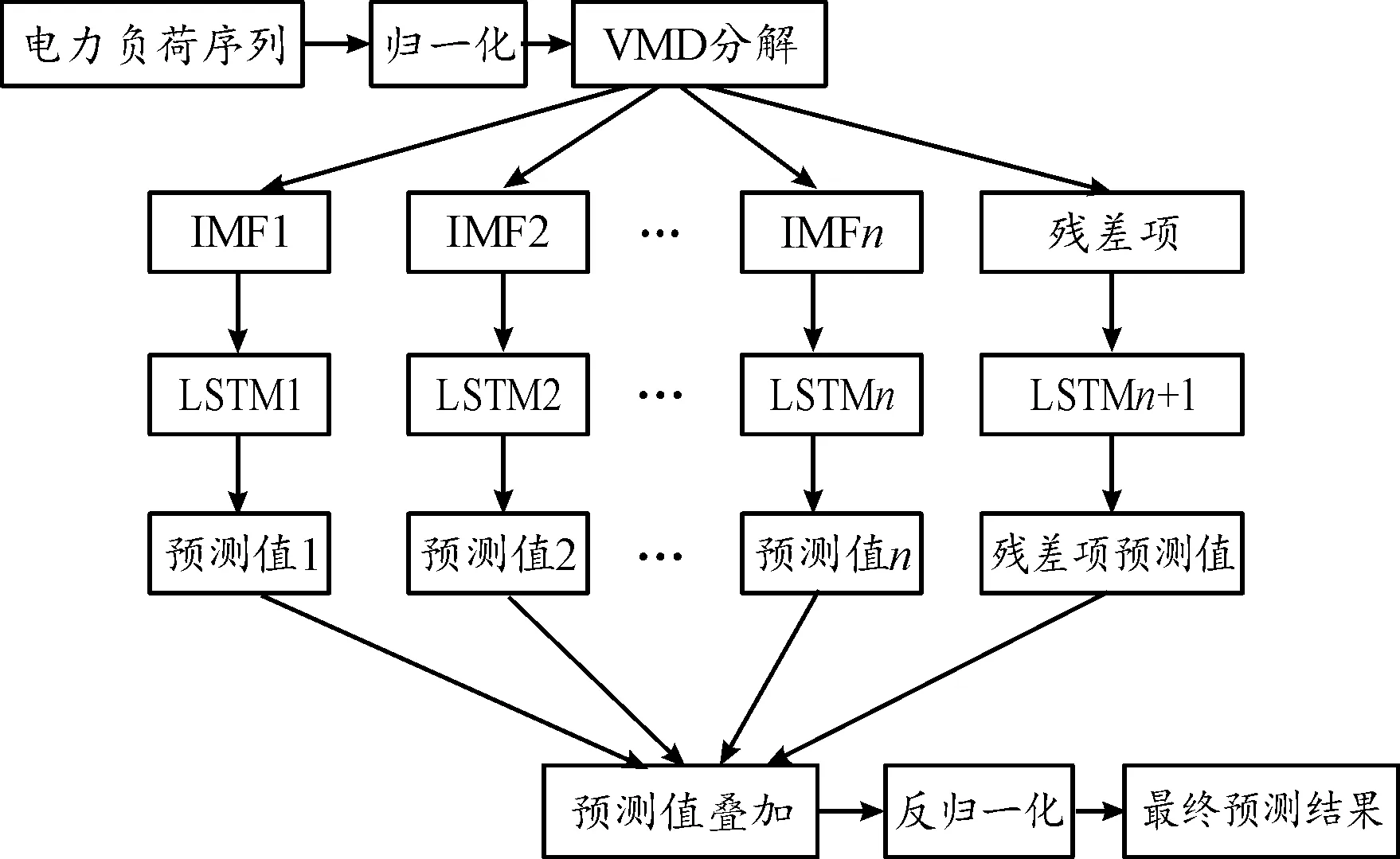
图2 预测模型流程框图

3 算例分析

3.1 实验数据和实验平台

实验以2016年电工数学建模竞赛[20]中提供的某地区2014年4月7日—22日的电力负荷为原始负荷数据，数据的采样周期为15 min，每天产生96组数据，共1 536组数据。以2014年4月7日—20日数据为LSTM神经网络的训练样本，以2014年4月21日的负荷数据为LSTM神经网络测试样本。预测2014年4月22日的电力负荷，并与实际负荷进行对比。

使用Intel Core I5处理器，16G内存，512G固态硬盘作为实验所用的硬件设备；使用Windows平台的Python3.8语言实现各种算法，采用Keras框架下的LSTM模型。

3.2 电力负荷数据归一化及分析

神经网络采用基于梯度下降的反向传播算法进行训练，数据过大或过小都难以寻找到最优解[21]。因此，采取归一化处理将样本数据转化为无量纲的纯数值，这样不仅能够提升模型的收敛速度，而且可以提升模型的精度。归一化公式为：

(16)

式中：Z′为归一化后的样本值；Z为原样本值；Zmax为原样本集中的最大值；Zmin为原样本集中的最小值。归一化后的原始电力负荷数据如图3所示。

图3 原始电力负荷数据曲线

从图3中可以看出，电力负荷数据有相似的波动规律，总体上与时间存在一定的周期关系。

3.3 评价指标

目前用于评价负荷预测结果的主要评价指标为平均绝对百分误差和均方根误差，其中MAPE反映了模型的拟合度，RMSE反映了预测的准确性。这两个指标的数值越小，模型的预测效果越好[22]，2种评价指标的表达式如下：

(17)

(18)

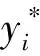
3.4 实验分析

通过多次实验测试，VMD算法参数设置如下：模态个数K=4；惩罚因子α=2 000；收敛判据r=10-7；起始中心频率ω=0。归一化后的电力负荷数据由VMD算法进行分解，分解后得到各模态如图4所示，残差量如图5所示。

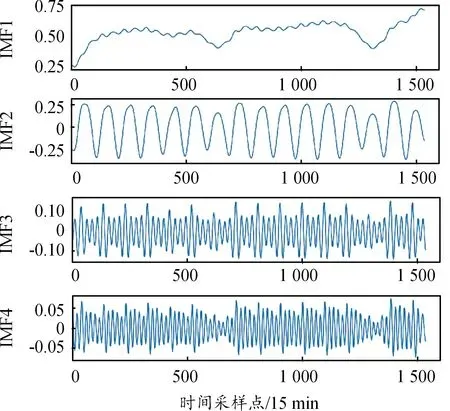
图4 VMD分解后的模态曲线

图5 VMD分解后的残差量曲线

从图4中可以看出，经过VMD算法分解后各模态分量的规律性比图3中原始负荷的规律性更强，更有利于神经网络对电力负荷数据特征的学习。从图5中可以看出，分解残差量介于模态分量IMF3与IMF4之间，残差量中含有丰富的信息，如果在建立模型时直接抛弃残差量，将会对模型的预测效果造成不利影响。

通过多次训练对比，选取LSTM模型参数值如表1所示。

Dropout参数随机抛弃每个输入的一些特征来增强模型的鲁棒性。这是通过不断改变网络的结构，使神经网络记住隐藏在数据中有规律的特征，而不是训练数据本身。在输入中使用过拟合参数，即输入到每个LSTM模块的数据将以一定的概率在正向激活和反向权值更新过程中失去其特征。

表1 网络主要超差数值

将分解后的各分量输入LSTM预测模型进行预测，得到各分量的初始预测值；然后，对初始预测值反归一化得到实际预测值；最后，各成分的预测值相互叠加，得到最终的预测结果。

为了评估模型的精确度，进行LSTM模型、VMD-LSTM模型和考虑分解残差量的VMD-LSTM模型预测值与实际值曲线对比，如图6所示。

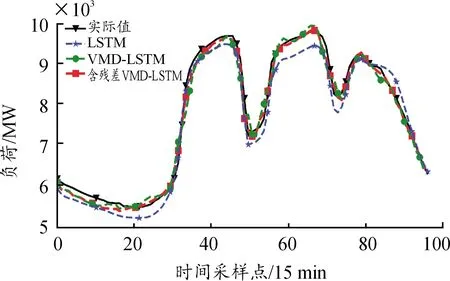
图6 3种模型预测曲线

经计算，得到3种预测模型预测结果的MAPE值和RMSE值，如图7所示。

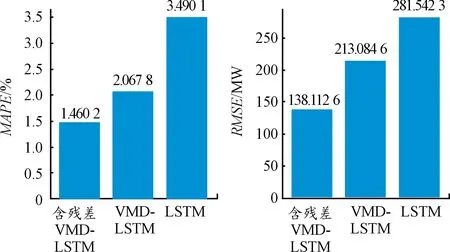
图7 3种模型预测结果的直方图

从图6、7可以看出，在考虑VMD分解残差量时的VMD-LSTM预测模型预测效果最好，MAPE值为1.460 2%，RMSE值为138.112 6 MW，验证了使用该方法预测精度有一定提升。

4 结论

针对电力负荷特性建立了考虑VMD分解残差量的VMD-LSTM预测模型。采用VMD算法对电力负荷进行分解，得到不同频率的IMF分量和分解残差量。使用LSTM神经网络对分解的各IMF分量和残差量数据进行预测，将预测结果叠加，得到电力负荷预测结果。实验结果表明，该预测模型具有较高的预测精度，电力负荷的趋势预测更加准确。下一步，将对研究方法做进一步改进和完善，在模型输入中加入气象、节日等影响负荷变化的因素，使预测效果更加符合实际需求。