固相反硝化微生物系统处理低碳污水动力学性能及经验模型研究

吴 恒，赵婷婷，陈爱玲，张 千

(重庆理工大学 化学化工学院， 重庆 400054)

水体富营养化是发生范围最广、危害程度最大的主要污染问题之一，而地表水体中氮素积累的重要原因之一是城镇污水厂尾水过量氮排放[1-2]。为降低氮素排放，城镇污水厂被要求进行提标改造，尾水水质必须达到一级A排放标准[3-4]，但城镇生活污水低碳化趋势给污水厂的提标改造带来了巨大压力[5-6]。目前，为了应对低碳源条件下总氮去除不达标的问题，大多数城镇污水厂采取增设深度处理工艺的方式，如生物滤池工艺，但该工艺在处理低碳污水时存在反硝化过程缺少电子供体的问题，导致脱氮效果差[7-8]。为此，城镇污水厂常采用外加碳源的方式对工艺补充碳源，虽然保证了脱氮效果，但易造成二次污染、运行成本高[9-10]，对适用于低碳源废水处理的脱氮新技术的研发显得尤为急迫。

鉴于此，研究以PBS作为BDPs，构建了SPD脱氮工艺，通过序批式实验探究了该工艺单位生物膜硝化、反硝化性能，同时，通过非线性拟合获得了碳源静态释放动力学方程。此外，在单级经验模型基础上推导了多级经验模型表达式，并将实测数据与预测数据进行了相对误差计算以判断其准确性，以期为SPD脱氮工艺的工程应用提供实践与理论基础。

1 材料与方法

1.1 实验装置

如图1(a)所示，SPD反应器由厚度为5 mm的有机玻璃材料构成，高20 cm，直径18 cm。反应器共分2层，外层水浴保温层，保持反应器温度恒定；内层内径8 cm，为反应器主体部分，PBS固体碳源填充率30%，废水有效体积为0.58 L，底部安装微孔曝气盘提供氧气。 如图1(b)所示，浸出性能实验装置采用密闭磨口锥形瓶，短管与弯长管分别用于取样与曝氮气。

1.2 实验用水

图1 SPD工艺实验装置示意图

1.3 实验填料

PBS购自深圳光华伟业公司，具体参数如表1所示。

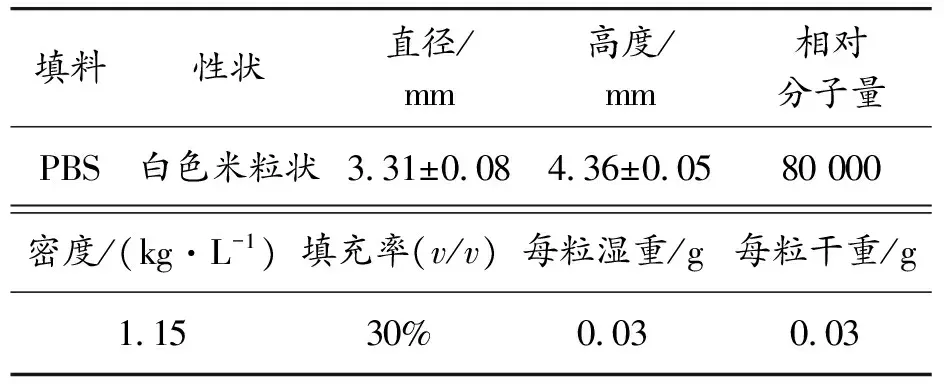
表1 碳源填料参数

1.4 研究方法

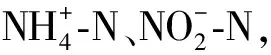
(1)

(2)

浸出性能实验：在温度为25～30 ℃条件下，取250 mL磨口锥形瓶进行PBS碳源的浸出性研究，取10.00 g PBS放置于加有100 mL蒸馏水的锥形瓶中，排空后密封，置于暗处，每天换蒸馏水，第1 d测定COD(chemical oxygen demand，COD)值，此后每隔5 d测1次，连续测52 d[19]。

1.5 分析项目及方法

2 结果与讨论

2.1 硝化反硝化动力学研究

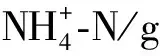
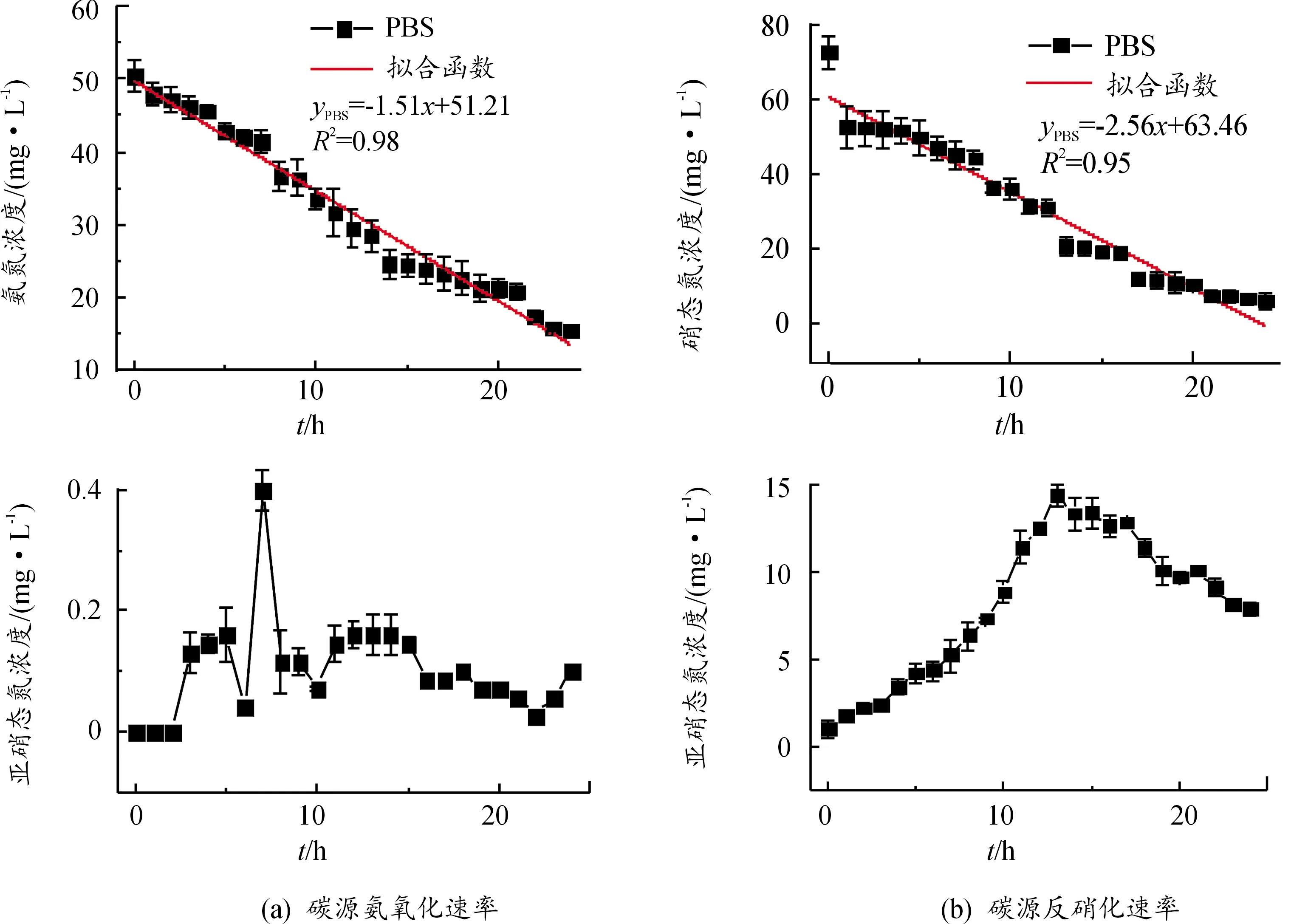
图2 脱氮动力学测定曲线

2.2 碳源静态释放动力学模型

探究了PBS在静态条件下的COD的释放规律，由图3可以看出，PBS第1 d COD释放量较低，第6 d COD释放达到峰值295.83 mg/L，这可能是此类聚合材料被浸泡后逐渐释放COD的缓释达峰过程，可见PBS的缓释达峰过程为6 d，第16 d后COD释放趋势逐渐平稳，第41～52 d，碳源释放浓度稳定在10～20 mg/L之间，第52 d仅为12.50 mg/L。有研究报道碳源在有微生物的条件下可以被靶向降解[16-17]，而此条件下采用蒸馏水进行实验，无微生物干扰，因此，碳源释放浓度逐渐降低且趋于平缓。但PBS在初期COD释放波动较大，说明在工艺启动初期可能会造成有机物超标的风险。需要注意的是，初期的过量碳源释放可以通过增加曝气量或延长水力停留时间来提高碳源利用率和COD去除率[25]。将第6～52 d的碳源浸出数据进行非线性拟合，可以发现PBS的碳源浸出规律符合对数方程y=-72.15ln(x)+273.02，说明在启动6 d以后，PBS在不同时间释放的COD浓度可以进行预判，对于基于PBS的SPD工艺启动过程具有一定的指导作用，以防止工艺在启动初期存在出水有机物超标的风险。因此，SPD工艺启动初期需要采取措施管控出水有机物浓度，而6 d以后可以通过模型进行COD释放预判。

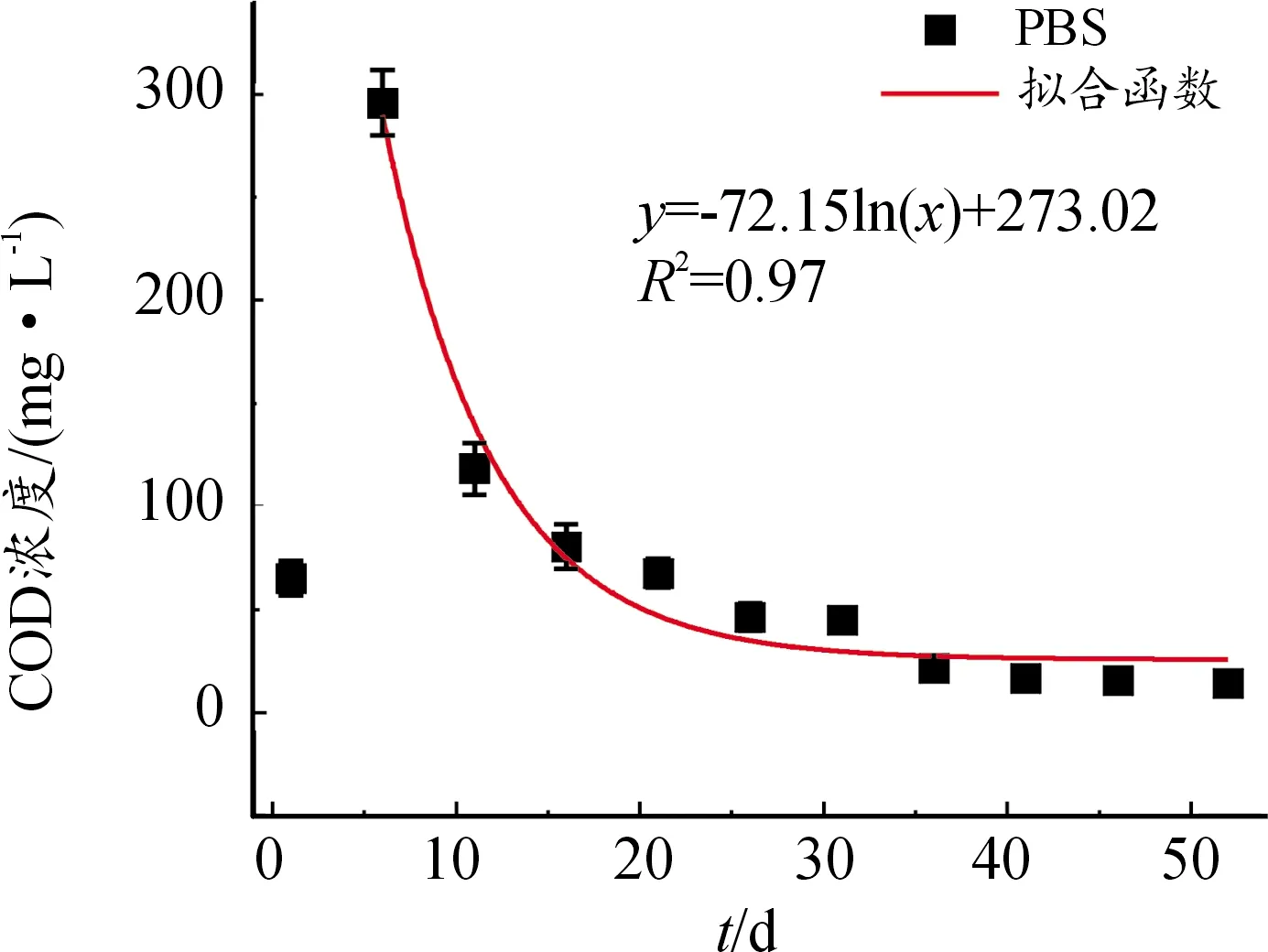
图3 碳源静态浸出性能曲线

2.3 SPD工艺模型建立

米门方程常用于生物膜反应器基质降解过程的推导，本文也根据该方程进行模型推导，在实验数据基础上计算模型参数，从而获得经验模型。齐勇等[26]采用米门方程进行了推导，认为在反应器内微生物系统对机智的降解过程符合一次反应关系，其生物反硝化动力学表达式为：

V=Vmax·Se/(Ks+Se)

(3)

将V=-ds/dt代入式(3)得：

-ds/dt=Vmax·S/(Ks+Se)

(4)

-ds/dt=Vmax·S/Ks

(5)

令K=Vmax/Ks，

得到

-ds/dt=K·S

(6)

当水力混合特性为推流时，积分得：

Se=S0exp(-Kt)

(7)

2) 反应器的特性接近推流。本研究采用的小试在时间上符合推流模式，符合要求；

对式(7)两边求对数得：

ln(Se/S0)=-Kt

(8)

根据ln(Se/S0)对t作图，见图4，得出K=0.08，因此可以得出：

S1=S0exp(-0.08t)

(9)

图4 ln(Se/S0)与t之间的关系图

2.4 多级SPD工艺模型建立

为了对本单级经验模型进行拓展，结合了相关的理论基础进行推导。徐斌等[27]对连续流的生物膜反应器进行了经验模型推导，本实验在其基础上进行了调整。在本实验中，不考虑反应器内的水动力学变化，仅从宏观上以连续运行的方式进行考虑，可以得到方程(10)，其中Q为进水流量；A1和A2分别为第1级、第2级反应器体内填料总体积；S0、S1和S2分别为原水、第1级和第2级反应器内的硝酸盐浓度，V1和V2分别为第1级、第2级反应器的体积。

QS0-V1A1=QS1

(10)

QS1-V2A2=QS2

(11)

对于多级串联反应器，其中的K级反应动力学方程为：

QSk-1-VkAk=QSk

(12)

其中：Vk需要进行推导。

实际上，根据式(9)可以进行以下变形：

(S1-S0)/t=[S0exp(-0.08t)-S0]/t

可以得出：

V=[S0exp(-0.08t)-S0]/t

(13)

QSk-1-[S0exp(-0.08t)-S0]/tAk=QSk

(14)

S1=(QS0-V1A1)/Q

S2=(QS0-V1A1-V2A2)/Q

S3=(QS0-V1A1-V2A2)/Q-V3A3/Q=

(QS0-V1A1-V2A2-V3A3)/Q

…

即为多级模型的具体表达式：

Sk=(QS0-V1A1-V2A2-…-VkAk)/Q

(15)

因此，根据上述可以整理得出基于米门方程的SPD工艺多级经验模型为QSk-1-[S0exp(-0.08t)-S0]/tAk=QSk，具体表达式为Sk=(QS0-V1A1-V2A2-…-VkAk)/Q。

2.5 模型应用与预测

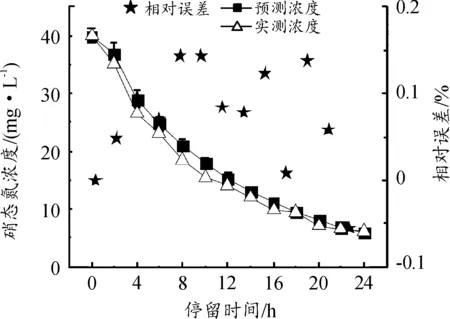
图5 模型预测实测对比图

3 结论

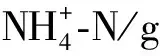
2)在SPD工艺启动初期需要采取措施以管控碳源出水浓度，如增加曝气、延长水力停留时间等。碳源释放峰值期后的碳源浸出规律符合对数方程y=-72.15ln(x)+273.02，可以据此预判碳源释放情况。

3) 基于米门方程推导出SPD工艺的单级经验模型为S1=S0exp(-0.08t)，而多级经验模型表达式为QSk-1-[S0exp(-0.08t)-S0]/tAk=QSk。

4) 该模型最大误差为13.80%，随着运行时间越久会出现2个趋势：误差随运行时间的变化可能越大，由正误差转为负误差。模型在长时间预测方面需要进行改进，但是对于SPD工艺的应用具有指导意义。