卷绕式锂离子电池单体有限元建模方法研究与实验验证

曲 杰，黄美华，王 超，刘明建，杜显赫

(1.华南理工大学 机械与汽车工程学院， 广州 510641； 2.维沃移动通信有限公司， 广东 东莞 523000)

在锂离子电池的设计制造过程中，系统设计师和制造商使用的方法往往是先测试、再制造。若要将锂电池作为部件置于手机或其他电子设备中进行整体仿真计算，则需要开发一个具有高计算效率和准确性的计算模型，这对于减少昂贵的测试费用、缩短测试周期是必不可少的。

兰凤崇等[1]对车用动力电池进行局部球痕挤压和平面挤压试验，采用均质化建模方法建立的电池模型预测了2种工况下的载荷-位移曲线及短路失效时刻。Wang等[2]建立了一种袋式锂离子电池的各向异性均质化有限元模型，该模型的18个参数通过不同加载条件进行标定，最终建立的模型能够合理预测电池整体屈曲行为。Sheikh等[3]针对18650圆柱形锂离子电池采用同心分层成型方法建立了一种电池分层模型，每层厚度为0.3 mm，共模拟了27层，仿真结果表明所开发的模型能够准确捕获电池的机械和热响应。Wang等[4]基于18650圆柱形电池中正负极、隔膜等部件的实际试验结果建立这些部件材料的本构模型，以及包含隔膜、正极、负极和电池外壳的电池详细计算有限元模型，所建立的模型能够很好地预测电池在径向压缩、压痕、弯曲和轴向压缩下的力学行为，并在加载条件下很好地捕捉单元的变形，为基于隔膜应变状态进行电池短路预测提供了参考。Lee等[5]通过考虑材料的非线性，包括应变率效应和材料各向异性引起的硬化，开发了一种非线性机械详细分层(NDL)模型，以准确预测由于LIB电池的非线性行为和隔膜破裂而产生的内部短路。该模型准确预测了在3种不同直径压头的准静态压痕试验下由于隔膜断裂所引起的载荷-位移响应和内部短路时刻。Kulkarni等[6]提出并分析了堆叠锂离子电池的不同有限元建模方法，包括非均质方法、均匀方法、混合方法和夹层方法。对于每种建模方法，均创建了一个电池模型，并从模型复杂性和仿真时间2个方面对模型进行了分析比较。Orhan等[7]提出了一种袋式电池单元力学建模方法，通过建立均质材料模型来表征单元的压缩、拉伸特性以及失效准则，并通过准静态和冲击载荷验证了电池有限元模型的有效性。所建立的电池有限元模型同时具有考虑单元的压缩和拉伸特性、易于原型化、节省时间等优点。Raffler等[8]提出了一种基于参数化梁单元的圆柱形锂离子电池力学建模方法，并通过离散梁公式定义各向异性材料行为。在仿真过程中，建立了考虑电池正极变形和径向变形的短路预测准则。所建立的电池模型与由实体及壳单元组成的典型单元模型相比，可以减少90%的总CPU计算时间。

目前，锂离子电池建模研究中的电池类型主要为卷绕式圆柱形电池、层叠式方形电池，而对卷绕式方形锂离子电池的建模研究较少。现有文献中关于锂离子电池建模的方法主要有2种，一种是均质化建模，另一种为细致化建模[9-10]。但在现有研究中，采用均质化建模方法来建立电池均质化模型以预测电池的机械响应、热响应或者内短路故障的相关研究居多，在电池细致化建模和电池模型简化方法研究中，一种兼求高计算效率、仿真结果准确的电池模型建模方法仍属空白。

本文中基于拆解的卷绕式方形锂离子电池的具体结构，采用代表体元法开发了一种包含铝塑膜、电池电芯、底黄胶、热熔胶、极耳等部件的精细化电池有限元模型，同时进一步将电池电芯的每个微观层按比例放大，得到2种简化的电池有限元模型。对电池进行平面挤压试验，对3种电池模型进行平面挤压仿真，通过对比实验和仿真结果验证仿真模型的有效性。通过分析3种模型计算时的耗时、内存占用率比较其计算效率。采样局部球头挤压试验以验证简化模型受局部载荷下的机械响应的准确性。构建的精细化电池模型可为不同机械载荷条件下的力学响应特性、内部短路机理和失效破坏研究提供基础。简化的电池模型可被置于汽车中或电子设备中进行相关性能的整体仿真分析。该电池模型的简化方法可为电池有限元模型的简化研究提供思路。

1 锂离子电池的结构及建模基础

1.1 电池结构

常见的锂离子电池可按照电池外形分为圆柱形锂离子电池、方形锂离子电池和纽扣式锂离子电池；按照外壳材质分为钢壳锂离子电池、铝壳锂离子电池和铝塑膜锂离子电池；按照电芯生产工艺的不同分为卷绕式和层叠式。电池内部主要由含锂化合物的正极材料、电解质、隔膜、负极材料(石墨)和外壳等5个部分组成。其中，正极片由正极集流体和涂覆在集流体表面的正极活性涂层组成，负极片由负极集流体和涂覆在集流体上的负极活性涂层组成，较厚的涂层可实现更高的能量存储，较薄的涂层可提高功率性能，隔膜则处于正极片和负极片之间以避免正负电极的直接物理接触，防止电路短路，同时保证电解质内锂离子尽可能地在正极和负极之间自由传导。正负极片和隔膜经堆叠或者卷绕成电池电芯后装入电池外壳中，经注液、封口、化成及老化等工序后批量生产出锂离子电池。图1所示为研究的卷绕式方形锂离子电池。

锂离子电池在承受各种载荷时的机械性能取决于其“形状因素”，“形状因素”主要由电极/隔膜等组件的特定布置决定。所研究的方形软包锂离子电池的电芯由石墨阳极、钴酸锂阴极和隔膜卷绕而成，最外层由铝塑膜进行包裹。电池基本特性：长度为84.6～85 mm,宽度为58～60 mm,厚度为4.5～4.6 mm，额定容量为4 920 mAh/18.94 Wh，典型电容量为5 000 mAh/19.25 Wh，放电温度为≤70℃，标称电压为3.85 V，充电截止电压为4.4 V，电池质量为135 g。

1.2 电池电芯微观代表体元模型

如图2所示，对电池进行拆解，研究电池的内部具体结构。当展开拆解后的电池电芯时，可以看到电池电芯由阴极-隔膜-阳极交替组成，采用卷绕折叠工艺而不是堆叠工艺制成。除此之外，还发现阳极和阴极涂层很容易从集流体上断开，类似于1叠卡片。同时，可以观察到共有15块独立的铜阳极板、13块双面涂层铝板和4块单面涂层铝板，中间由隔膜隔开，如图2所示。

图2 电池拆解图

组成电池电芯的集流体、隔膜和活性物质的微观力学性能对电池的力学特性和失效机理影响很大。因此，建立高精度的锂离子电池有限元模型的关键在于建立电池电芯的细致模型。由于电池电芯由隔膜、活性物质和集流体组成，且隔膜的各向异性和其独特的分层结构导致整体表现出各向异性，因此虽然隔膜非常薄(8 μm)，与电极的铝/铜箔的强度相比较弱，但它对整体强度的贡献仍不可忽视[11]。

综上所述，该电池电芯由多个微观层状物质卷绕而成，每层包含8个重复单元，称之为代表体元(representative volume element，RVE)[12]。1个RVE层包括2层阴极活性物质，2层阳极活性物质，1层阴极集流体(主要是铝箔)，1层阳极集流体(主要是铜箔)和2层隔离膜。通过对电池进行拆解发现，研究的电池电芯由15个RVE单元组成，即120层微观层组成。将电池进行拆解，并在实验室测量获得电芯各层的微观材料厚度，结果如表1所示。

表1 RVE及各层厚度 μm

2 卷绕式锂离子电池有限元模型开发

2.1 建模分析及单元选择

正极片由铜箔和涂覆在铜箔表面的活性涂层组成，负极片由铝箔及涂覆在铝箔上的负极活性涂层组成。本文中所研究的电池铝箔厚度为8 μm，铜箔厚度为7 μm，涂层厚度大约是集流器厚度的7～8倍。当电池在承受机械载荷时，主要承载能力依靠铝箔和铜箔，涂层作为一种多孔材料起到辅助作用，因此铝箔及铜箔的性能非常重要[13]。

从已发布的文献来看，部分学者采用均质化建模方法，将正极、负极、隔膜采用共节点法建模为一均化的物质，这种建模方式网格数量可控，但难以将电芯微观特性表示清楚。还有学者将活性物质涂层、铝箔、铜箔和隔膜采用实体单元单独建模，但根据有限元理论，单元的2个方向尺寸比应在5:1以内才能有较准确的结果。由于铝箔、铜箔的厚度通常只有几微米，因此要求模型网格尺寸非常小。这种建模方式计算精度高，但用于解决实际工程问题时计算效率低，难以直接应用。

为解决上述问题，将铜箔、铝箔划分为壳单元，既可以有效减少网格数量，也满足有限元理论的要求。涂层采用实体单元划分。对于锂离子电池的隔膜，其在18650等大部分类型的电池中的厚度为20～25 μm，因此国内外学者常采用实体单元对隔膜进行建模[14]。由于本文中研究电池的特殊性，隔膜的厚度仅为8 μm，故考虑到网格数量的控制，将电池模型中的隔膜也划分为壳单元。经实验室测量验证，电芯外面包裹的铝塑膜厚度为86 μm，同时考虑到铝塑膜边缘的不规则性及其在受到机械载荷时容易产生褶皱的问题，若划分为实体单元不易得到准确的褶皱变形效果，故最终将其划分为壳单元，且壳单元可以减少计算量。考虑到极耳、热熔胶、底黄胶对电池强度具有重要影响，因此建立的电池模型(包括上述部件)均采用实体单元进行网格划分。

2.2 网格划分

基于各部件的单元类型分析，将采用三维建模软件Catia建立的电池三维模型导入Hypermesh软件中,并对其进行网格划分。有限元网格划分是进行有限元数值模拟分析中至关重要的一步，它直接影响后续数值计算分析结果的精确性。网格数量直接影响计算精度和计算时耗，网格数量增加会提高计算精度，但计算时耗也会增加。当网格数量较少时增加网格，计算精度可明显提高，但计算时耗不会明显增加；当网格数量增加到一定程度后，再继续增加网格时精度提升很小，计算时耗却大幅度增加。因此，在确定网格数量时应权衡这两个因素进行综合考虑。

综合考虑计算精确性和计算速度后，在划分网格时将电池中间部分的尺寸划分为4 mm，对面内尺寸单元进行选择性改进，对边缘部分网格和卷绕部分网格进行多次局部加密，加密部分网格尺寸为0.3～0.7 mm。二维网格均采用四节点四边形单元，三维网格采用八节点六面体单元。1个RVE单元的网格数量为1.35 万，电池总的网格数量为22 万。建立的电池有限元模型如图3所示，各部件实体单元网格尺寸如表2所示。

图3 电池有限元模型示意图

表2 实体单元网格尺寸 mm

2.3 材料参数

由于所建立的电池有限元模型中的接触非常复杂且材料呈高度非线性，因此采用Abaqus显式模块模拟电池在外载荷作用下的响应。其中，铝塑膜、铝箔、铜箔、极耳、热熔胶、底黄胶用弹塑性材料属性定义。材料的属性参数从已发表的文献[15]及制造商处获得，如表3所示。

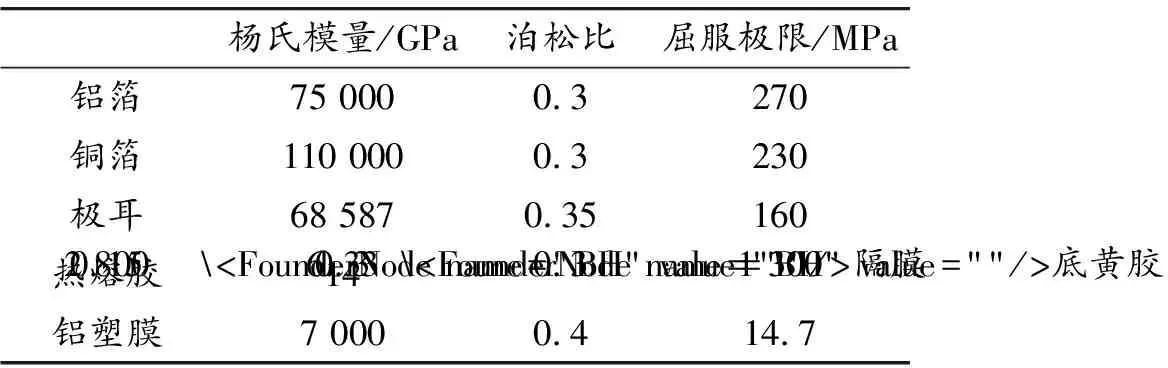
表3 材料属性参数

涂覆在正极集流体和负极集流体上的活性物质较为特殊，由于活性物质疏松多孔，几乎不能承受拉力方向的载荷，因此只需考虑压缩方向的屈服，用可溃缩泡沫材料来定义活性物质，材料参数如表4所示。

表4 活性物质材料参数

隔膜的弹性性质表现为正交各向异性弹性[16]，图4所示为隔膜拉伸和压缩的应力-应变曲线。国内外学者用可溃缩泡沫来定义隔膜。ABAQUS中可溃缩泡沫只能用于实体单元。鉴于所研究电池的特殊性，隔膜厚度只有8 μm，并划分为壳单元，因此用正交各项弹性模型表征隔膜的弹性行为，用各向异性Hill48屈服准则表征隔膜的塑性行为。

Hill48屈服准则为：

(1)

其中：F、H、G、L、M、N是和材料有关的常量，可以通过沿隔膜不同方向进行拉伸试验获得，即：

(2)

(3)

(4)

(5)

其中R11、R22、R33、R12、R13、R23为各向异性屈服应力比。正交各向异性弹性材料本构模型如式(6)所示。隔离膜材料参数见表5。

(6)

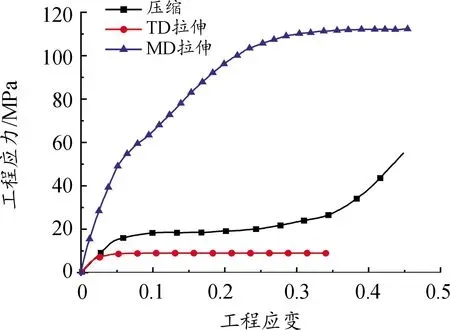
图4 隔膜拉伸和压缩应力应变曲线

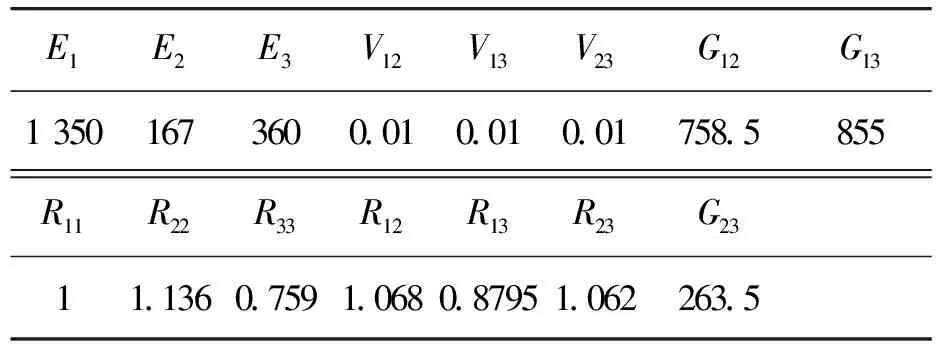
表5 隔膜材料参数

2.4 模型简化

拆解后的电池电芯共有15个RVE结构。按照1∶1建立详细电池有限元模型。考虑到实际工程应用，提出一种电芯模型简化方式，将每个微观层的比例近似放大(两层相当于每层的相应厚度)。用这种方法得到1个60层的电池有限元模型。随后，利用相同的方法对60层的电池进行同样步骤的简化，最终得到30层的电池有限元模型，为保留电池卷绕式结构最小单元，简化为30层后停止。简化原理如图5所示。

图5 模型简化原理示意图

最终建立3种电池有限元模型。第1种为由电池1∶1建模而成的120层详细模型，网格总量为22 W；第2种为对电池内芯的微观层每层比例放大2倍得到的60层电池模型，网格总量为11 W；第3种为对电池内芯的每层比例变厚4倍得到的30层电池模型，网格总量为5.6 W，其剖面如图6所示。

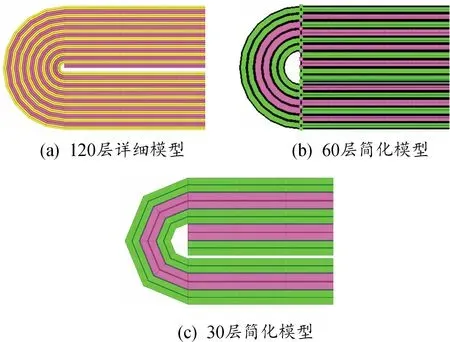
图6 电池电芯3种模型的剖面示意图

3 模型验证

3.1 平面挤压试验及电池模型比较验证

为了验证3种锂离子电池有限元模型的准确性，采用平面挤压试验来进行实际验证。由于实际情况下电池容易受到厚度方面的挤压，因此设计了沿厚度方向的平面挤压试验，试验设备包括1台MTS万能试验机和1台控制电脑。万能试验机用来加载力和位移，试验力的量程为0～100 kN，位移测量分辨率为0.01m，加载方向沿电池的厚度方向，加载速度为1 mm/min。由于实验室条件限制，加载力至85 kN停止。平面挤压试验实物如图7所示。

图7 平面挤压试验实物图

通过试验发现，整个过程没有发生内短路。当挤压即将结束时，力的大小接近MTS试验机的负荷极限100 kN。在这种情况下，电解液被从电池中挤出，有较浓的电解液味道，使电池体积发生了变化。活性颗粒的孔隙率可高达60%，空隙通常填充有电解质。尽管没有进行精确测量，但观察到样品在横向方向上的尺寸没有明显增加。这表明涂层材料的泊松比比较低。

在ABAQUS平台采用动态显示求解器对所开发的3种卷绕式方形锂离子电池模型进行平面挤压仿真计算。为确保整个过程保持准静态，质量缩放系数设置为1.5,平面挤压仿真图如图8所示。最终得到不同模型的仿真力-位移曲线及实际平面挤压试验的力-位移曲线(如图9所示)。

图8 平面挤压仿真图(隐藏上压板)

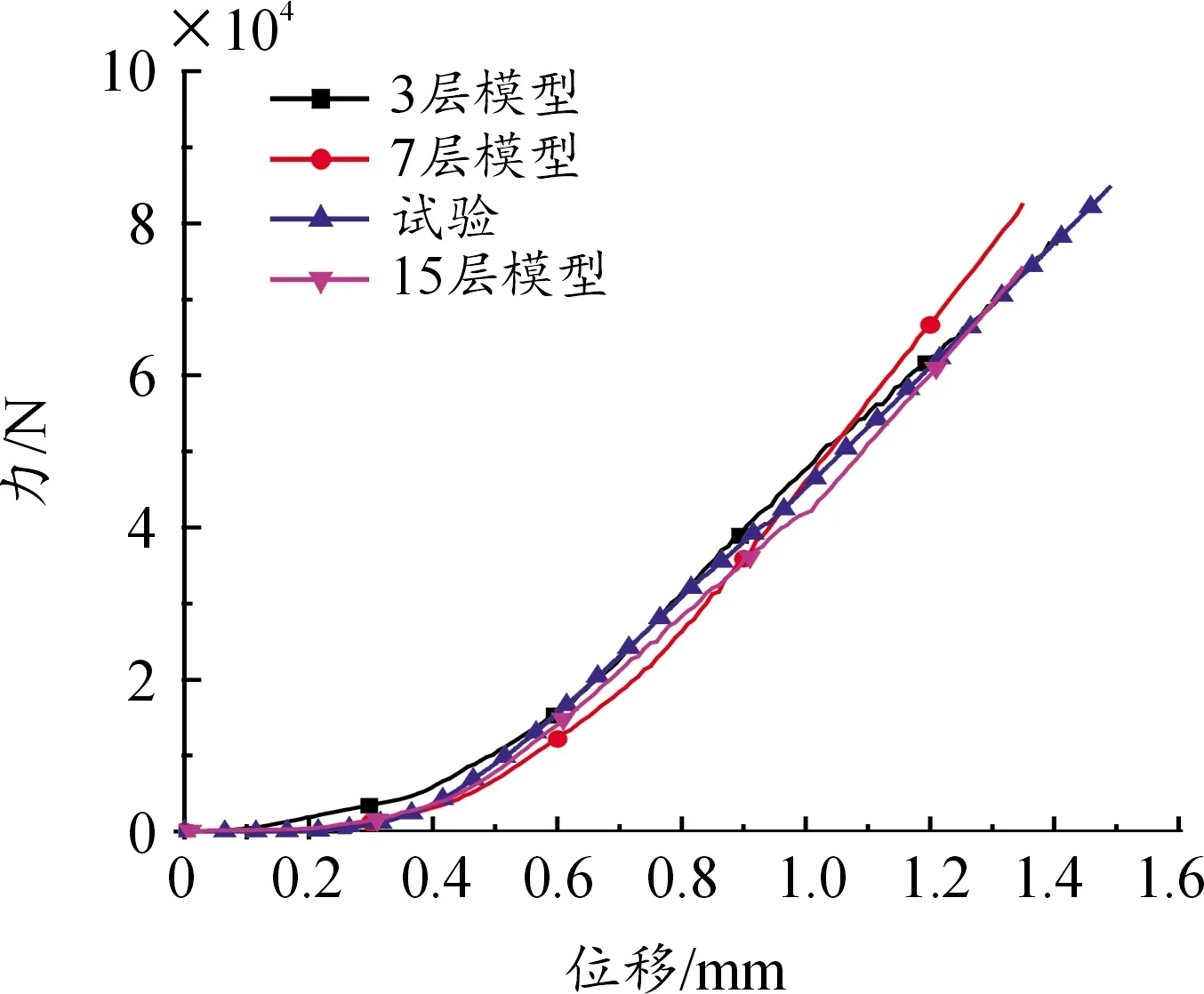
图9 不同模型仿真及实际试验下的力-位移曲线

由图9可知，3种模型的平面仿真结果与实际平面挤压试验结果一致，证明3种模型都是可靠的。不同模型的计算用时及能量耗散如表6所示。由表6可知，在10个CPU计算条件下，120层精细化模型计算时间为1 260 min，经过1次简化后，60层模型计算时间为138 min，而30层最简模型计算时间为58 min,即最简模型时间效率提升90%以上。同时，3个电池模型的动能、伪应变能与内能之比均在5%以内，说明沙漏可控且满足ABAQUS对准静态仿真的要求。仿真结果表明，30层简化模型相比120层模型的计算效率提高90%以上，内存占有率减少85%，所开发的3种模型可在误差允许范围内预测出电池在平面压缩情况下的力位移响应。综上所述，在不损失仿真精度的前提下，30层简化模型的计算效率和内存占用率为最优，也说明本文所提出的锂离子电池电芯模型简化方法的有效性。

表6 3种电池模型的计算耗时及能量耗散

3.2 局部球头挤压试验及电池简化模型验证

为进一步验证所建立的30层简化锂离子电池模型在局部载荷下能够准确反映相关力学响应，对30层简化模型进行局部球头挤压仿真,在锂离子电池相同位置进行局部球头挤压试验，得的载荷-位移曲线如图10所示。由图10可知，模拟结果和试验结果吻合较好，载荷峰值偏差不超过5%。仿真过程中伪应变能、动能与内能曲线如图11所示。由图11可知，伪应变能、动能与内能相比，均不超过5%，进一步证明了简化锂离子电池模型的有效性和可靠性。

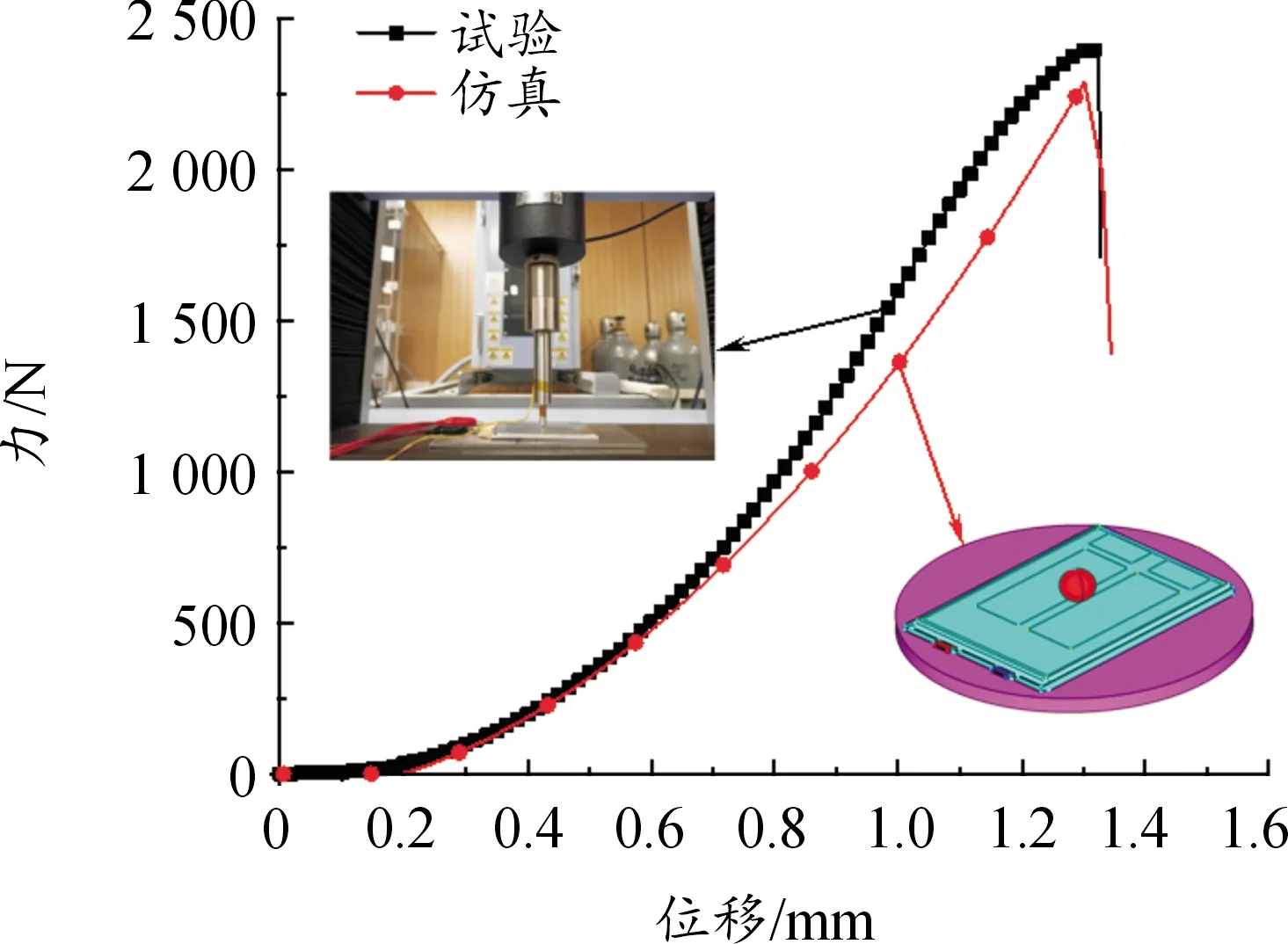
图10 局部球头挤压试验及仿真中的载荷-位移曲线

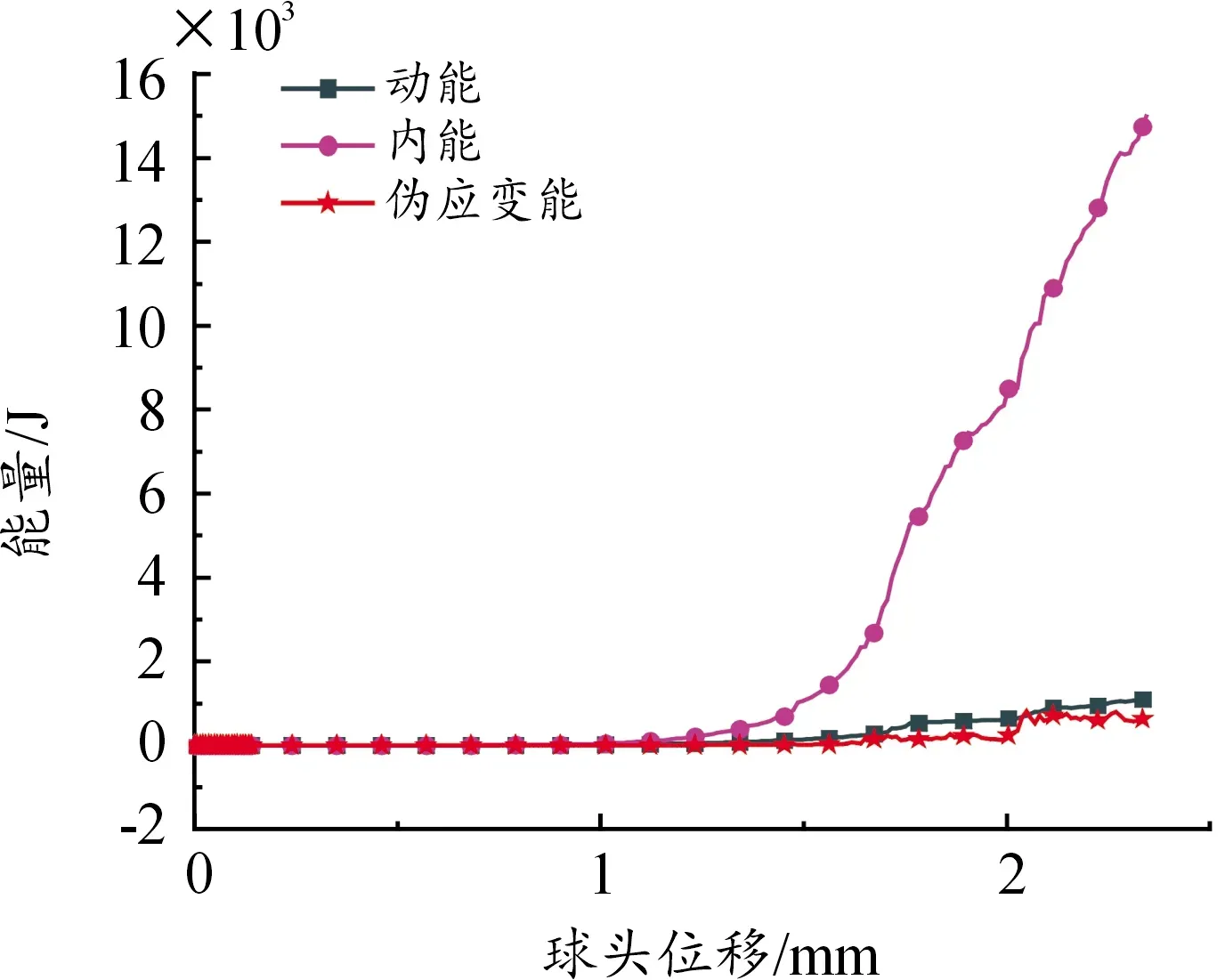
图11 球头挤压仿真时动能、内能及伪应变能变化曲线

4 结论

在基于卷绕式方形软包锂离子电池的详细结构组成及微观结构的基础上，开发了卷绕式方形软包锂离子电池的精细化有限元模型。该模型包括活性材料、集流体、隔膜等部件的详细表示，并进一步基于代表体元法开发了2种新的简化模型。所建立的3种电池有限元模型都能合理预测它们在平面压缩作用下的力学响应，但简化模型的计算效率和内存占用率更优。采用局部球头挤压试验进一步验证简化模型在局部载荷下的机械响应。研究结果为卷绕式方形锂离子电池在机械载荷条件下的变形响应特性提供了参考，对提高锂电池的安全性有重要的工程意义。研究这种简化模型的意义在于:

1) 开发高计算效率的计算模型可减少昂贵的测试费用，缩短测试周期。简化有限元模型可置于手机、汽车或其他电子设备中进行整体有限元仿真分析。

2) 为未来锂离子电池模型进一步简化提供思路。所开发的电池有限元模型也可用于模拟多层单元和模块RVE试样的力学试验。