基于Van der Pol方程的双脉冲射流控制机理研究

陆惟煜，李秋锋，傅 鑫

(1.南京工业大学 数理科学学院, 南京 211800; 2.中国飞行试验研究院, 西安 710089; 3.南京航空航天大学 能源与动力学院, 南京 210016)

压气机是航空发动机中的核心部件之一，提高压气机负荷是提高航空发动机推重比的有效途径。在目前的材料及气动设计水平下，提高压气机负荷面临着流动分离风险，需要引入高效的流动控制手段对流动分离加以抑制。

由于非定常流动控制相比定常方法能大幅节约能量注入[1]，因此其作为流动控制领域的前沿方向，受到国内外学者的广泛关注。针对非定常流动控制技术的研究主要分为3个方面：一是流动控制措施的研究，目前的流动控制措施主要包括声波激励[2]、合成射流[3]、脉冲射流[4]、振动壁面[5]、等离子体激励[6]等，这部分研究主要针对激励器(产生非定常激励的装置)结构形式、自身特性进行研究；二是针对各种流动控制方式参数的优化及流场相应特性的研究[1]，研究通常将流场视为黑盒子，采用数值模拟(如采用URANS[7])或实验的手段获取流场控制的总体效果(总压损失、升阻比等参数)与激励参数间现象层面的关系，并对激励参数进行定量层面的优化；三是针对非定常流动控制更深层次的机理研究，若将非定常激励视为对流动不稳定性的利用，通常可以采用线性稳定性理论中的经典稳定性分析(平行流O-S方程)[8]或二维全局不稳定性(bi-global)分析[9]预测最佳激励频率，若将非定常激励视为与流动非定常拟序结构发生了相干作用，通常可以采用POD[10]或DMD[11]方法分析激励作用前后流动拟序结构的变化，这些基于简化模型或拟序结构分析的方法不再将流场视为黑盒子，从而能够获得一定的流场控制内在机理。

本文研究针对上述非定常流动控制技术的第二、三方面展开。即针对现存非定常流动控制技术进行参数优化，以期提升控制效果；以及针对非定常流动控制理论模型欠缺及流动控制机理不明的问题，发展简化的非定常流动控制模型，揭示流动控制机制。具体而言，在常规的单脉冲射流技术的基础上，探索了双脉冲射流的参数选取规律，并基于流动的弱非线性稳定性理论，发展了适合于双脉冲射流的受迫Van der Pol模型，以用于初步解释双脉冲射流流动控制特性，揭示双脉冲射流流动控制的机制，为后续非定常流动控制技术的参数设计及机理研究提供理论参考。

1 理论模型与数值模拟方法

1.1 理论模型推导

首先针对双脉冲射流流动控制建立简化的理论分析模型，用于指导双脉冲射流的参数设计并揭示流动控制机理。由于非定常流动控制与流动不稳定性密切相关[12]，线性稳定性理论尽管发展较为成熟，却只能反映不稳定波演化的初始阶段，不能反映不稳定波的饱和阶段和旋涡卷起的过程。采用弱非线性流动稳定性理论中的S-L模型，该模型能近似反映不稳定波的饱和及受外界激励作用下的响应[13]。

流动分离中的大尺度分离涡由流动不稳定性产生，主导频率不稳定波的演化方程可表达为：

u(t)=A(t)sin(ω0t)

(1)

式中，A(t)为扰动幅值，ω0为扰动波频率。根据S-L理论[14]，扰动幅值的演化方程为：

(2)

(3)

将式(2)及其对时间的导数代入式(3)可得：

(4)

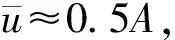
(5)

该方程即为自由Van der Pol方程[15]，其在初始扰动下能产生一定频率的自激运动，和流动不稳定性的物理本质相一致。对于双脉冲射流而言，扰动波的演化发展受外界周期性激励的作用，该作用可等效为在自由Van der Pol方程中增加2个受迫项，如下所示：

(6)

其中：Ae、ωe和φe分别表征外界周期性激励(此处为脉冲射流)的幅值、角频率和相位，下标1、2则用于区分双脉冲射流。为了便于分析，可将上式无量纲化，得到：

(7)

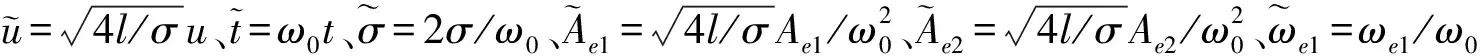
2.2 模型参数与评价指标

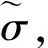
最后，为了将模型和实际流动控制相联系，需要引入模型的评价指标。通常在实际流场中引入总压损失系数评价流动品质，由于该模型具有不稳定性，在以K-H流动不稳定性为主导特征的自由剪切流中，常用卷入比衡量剪切流主导涡结构对高、低速主流间动量的传递率[1]。参考卷入比的概念，本文引入扰动波的有效值(均方根)的概念，其定义如下：

(8)

该式反映了利用流动不稳定性对动量的输送程度。该值越高，通常流动控制效果越好(分离区的低能流得到更多主流的动量补充)，为了和实际流动的总压损失系数变化趋势相一致，模型采用δ的相对减少量作为评价指标：

(9)

式中：δn和δc分别为无控和有控情形下模型的δ值。δ的具体计算首先利用Matlab软件求解不同参数下式(7)所示非线性常微分方程，再依据式(8)计算δ的具体数值，从而制作δ随各个激励参数的变化曲线。

2.3 物理模型与计算方法

本文基于典型具有分离流动的二维扩压通道，对双脉冲射流流动控制下通道内部流动进行了非定常数值模拟研究，以获得不同射流参数下双脉冲射流的流动控制特性，并与基于Van der Pol方程的理论模型进行对比分析。

扩压通道的几何造型如图1所示，其包含进口段、弯曲扩张段(仿叶片段)及出口段，进、出口宽度分别为34.3 mm和55 mm，弯曲段长(仿叶片弦长)为80 mm。在通道进口马赫数为0.1时，弯曲段背风侧出现流动分离，双脉冲射流即针对该流动分离进行抑制。

此外，本文在数值模拟中采用相对总压损失系数评价流动控制效果(与模型的评价指标-δ相对应)。其中，通道的总压损失系数的定义为：

(10)

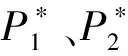
(11)

其中：ωn和ωc分别为无控和有控情形下通道的总压损失系数。

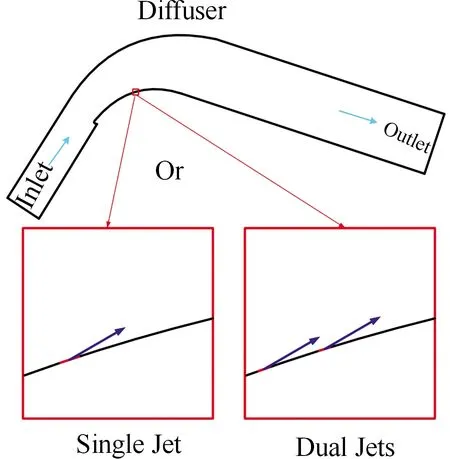
图1 扩压通道及双脉冲射流示意图

2 结果分析与讨论

2.1 无控特性

无控情形扩压通道的瞬时涡量云图如图2所示。

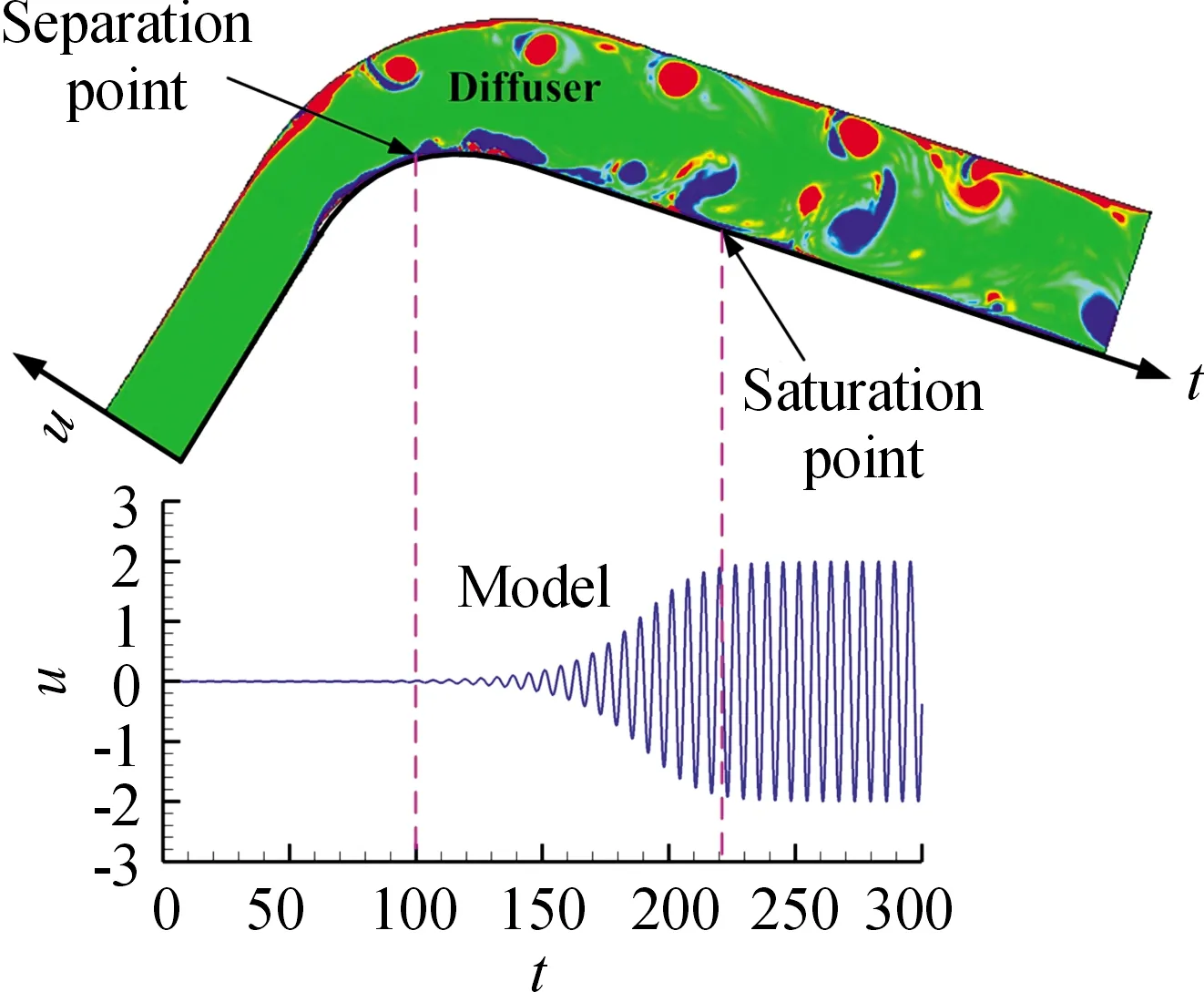
图2 无控情形下具有流动分离弯曲扩压通道模型

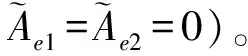
此外，无控状态下理论模型与扩压通道分离区数值模拟监测点处静压的FFT(快速傅里叶变换)频谱图如图3所示。其中，数值模拟结果已进行了无量纲处理。可以看出，理论模型与数值模拟结果都具有一个突出的主频(无量纲频率为1)，但数值模拟中除主频外的杂频相对理论模型更为突出。这是由于实际流动的复杂性所致，理论模型的模化作用则起到过滤这些杂频，仅保留与非定常流动控制密切相关的主导流动模式的目的。

图3 无控情形下数值模拟及模型产生的频谱图

因此，非受迫Van der Pol理论模型可以粗略地与实际非定常分离流发展的3个阶段相对应。这样施加合理表征外激励项的受迫Van der Pol理论模型有望描述脉冲射流流动控制的现象及机制。

2.2 有控频率特性

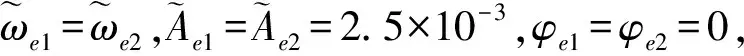
如图4所示，数值模拟的结果表明：控制效果在脉冲射流折合频率为1时最好，流动损失减少量达到9.2%，而其他激励频率下，总压损失变化量约在-3%～3%，控制效果较差，甚至有负效果。理论模型有着类似的预测结果，在激励折合频率为1时，损失减少量达到8.8%，而在其他激励频率下，损失变化量约在±1%之间。上述分析表明，脉冲射流的最佳激励频率与流场自然频率或系统主频密切相关，具有该频率的激励能更好地利用流动不稳定性达到流动控制目的。

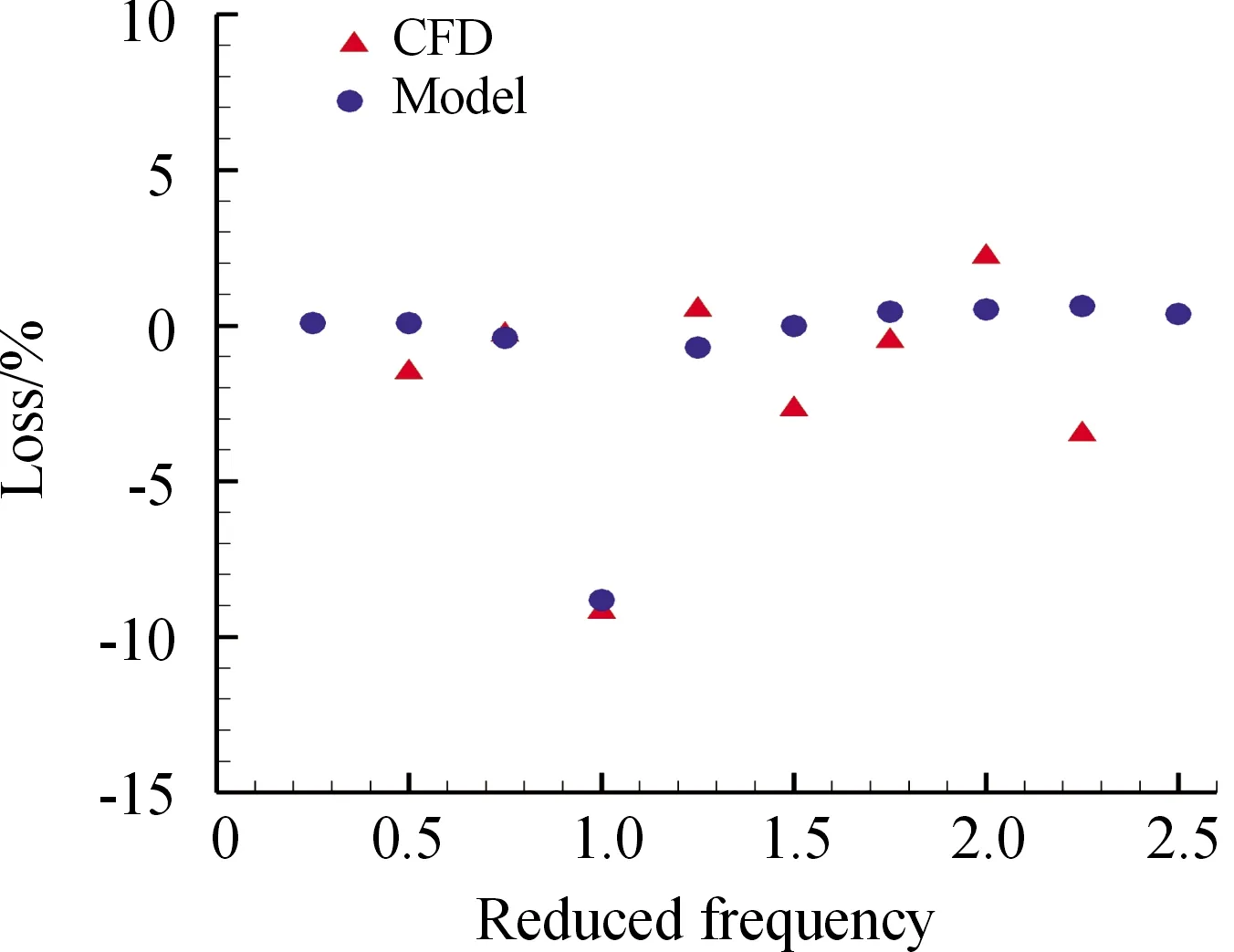
图4 不同频率下的相对损失系数(数值模拟及模型结果)

2.3 有控相位特性

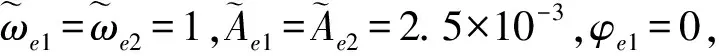
如图5所示，数值模拟与理论模型结果的总体趋势吻合得较好，都反映出双脉冲射流在同相时(Δφe=Δφe2-Δφe1≈0)控制效果最佳，而在反相时(Δφe≈±π)控制效果最差。在本文算例中，双脉冲射流相距位置较近，该结果表明：脉冲射流存在类似波的干涉效应，同相位脉冲射流能发生叠加，从而产生更好的控制效果，而反相位脉冲射流则发生相消，使激励的非定常性减弱，从而无法利用非定常流动控制“四两拨千斤”的效应。从数值模拟和理论模型中也可看出，在反相工况附近，控制效果接近零。

双脉冲射流的相位特性表明了非定常流动控制多个激励作动器间相位差控制的重要性，设计原则应使激励相叠加，而非抵消。

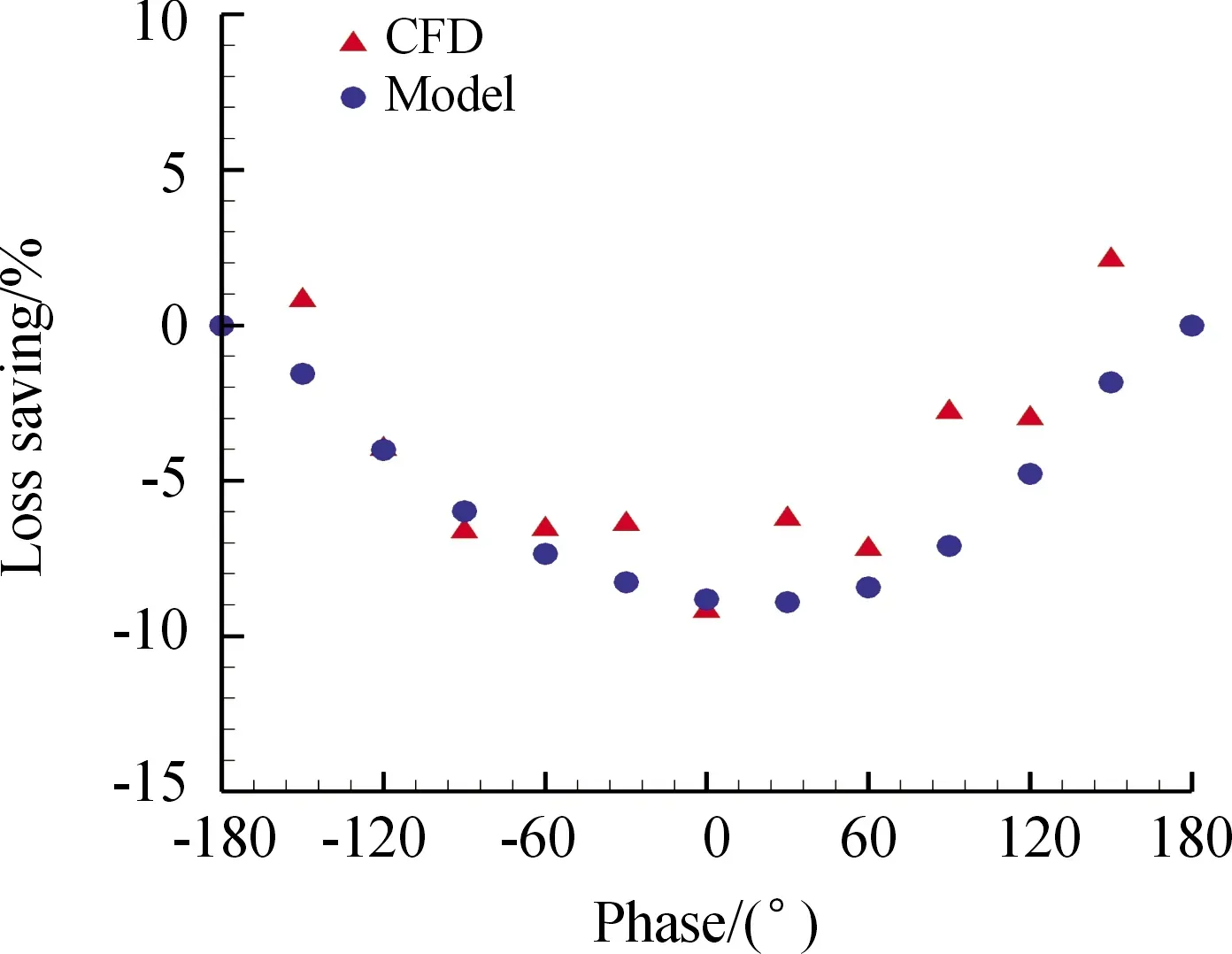
图5 双射流不同相位差下的相对损失系数(数值模拟及模型结果)

2.4 单、双脉冲射流对比及机理分析

本节重点分析双射流由于作用位置差异带来的影响。如表1所示，分别布置于分离点前后、折合频率为1的同相双脉冲射流(如图1所示)可产生9.2%的总压损失减少。而布置于分离点处、动量系数为双脉冲射流之和、折合频率为1的单脉冲射流只能产生5.4%的总压损失减少。这说明，由于双脉冲射流前后布置，其不能完全等效为单脉冲射流，双脉冲射流前、后的布置关系会带来额外的控制效果增益。

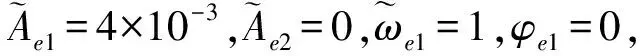
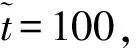
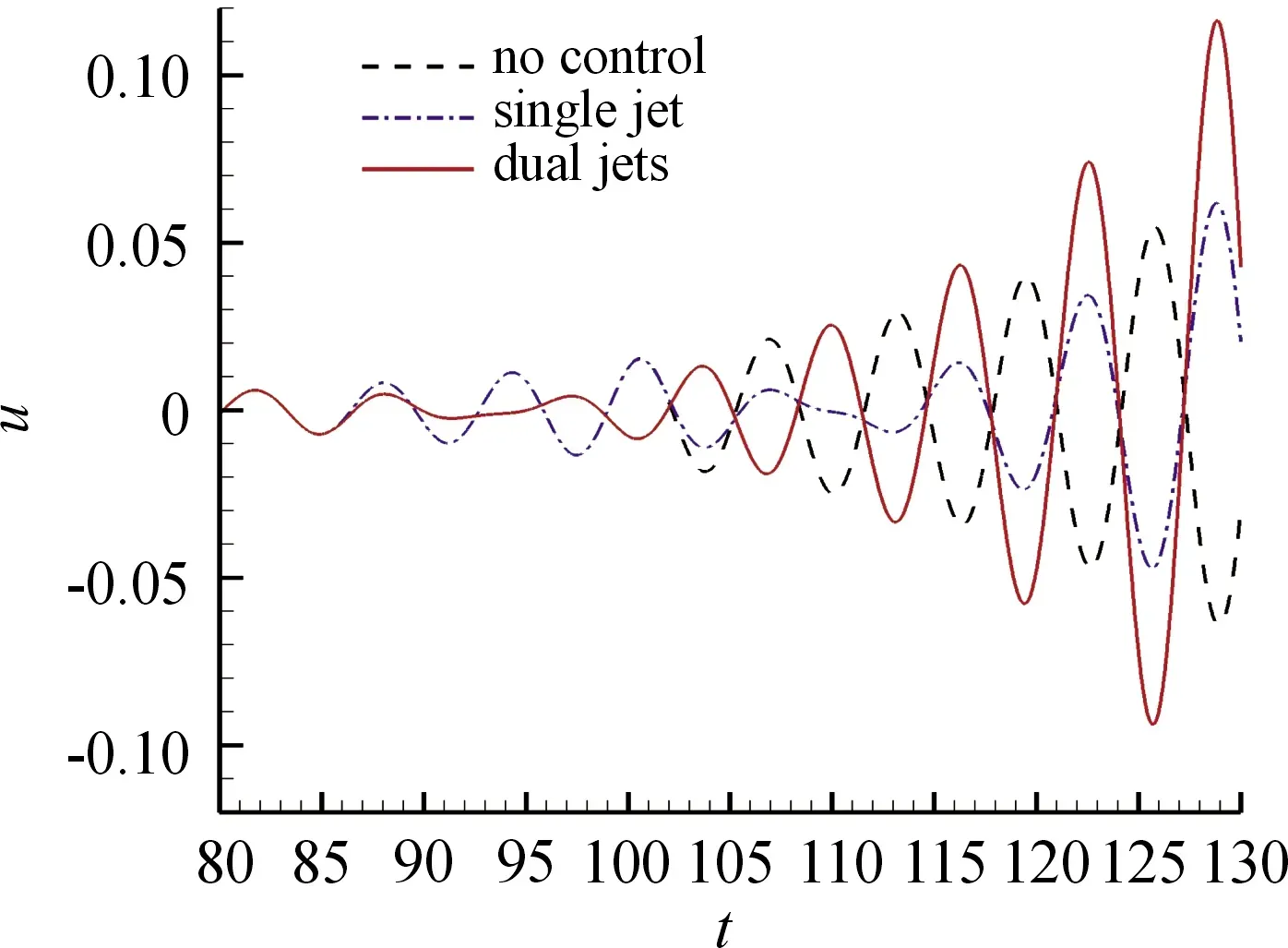
图6 无控、单射流、双射流情形下模型的时域曲线

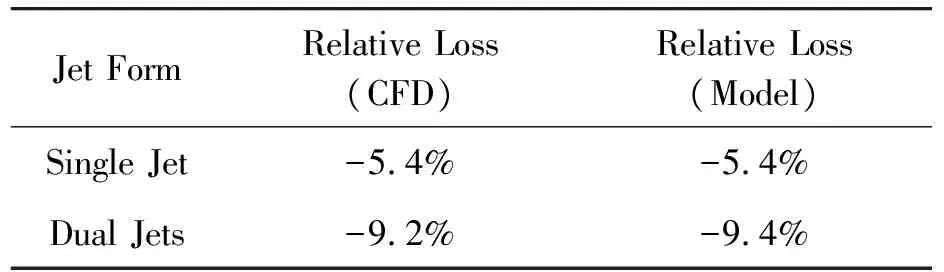
表1 单射流与双射流对比

3 结论

1) 提出了一种带两个受迫项的基于Van der Pol方法的理论模型，用以刻画双脉冲射流流动控制的频率特性及相位特性。理论和数值模拟均表明：布置于分离点附近的双脉冲射流折合频率为1，且相位相同时控制效果最佳。

2) 结合理论模型和数值模拟，本文认为双脉冲射流流动控制机制如下：频率特性表明，脉冲射流激励需利用分离流主导频率表征的不稳定性增强不稳定涡结构；相位特性表明，双脉冲射流间会发生相干作用，同相相叠加，异相相抵消；此外，双脉冲射流依靠上游射流的预同步机制，使射流更高效地向不稳定涡结构注入能量，利用该涡结构将主流动量传递至分离区，以达到抑制流动分离的目的。