交叉旋翼悬停气动性能和流场干扰

吴伟伟, 马存旺, 张 练

(中国航天空气动力技术研究院彩虹无人机科技有限公司, 北京 100074)

引 言

交叉旋翼是一种独特的旋翼构型, 具有结构紧凑、气动效率高的特点, 并且采用该构型旋翼的直升机重量效率很高, 如K-MAX直升机, 空重只有2 330 kg, 极端情况下可吊起3 100 kg的货物.

相对于单旋翼、共轴双旋翼等常规构型, 交叉旋翼的两幅旋翼旋转轴呈一定角度, 旋转中心距离很近.两幅旋翼的流场交叉影响, 互相处在对方下洗和尾迹涡中, 存在严重的涡-涡、桨-涡干扰等复杂的流动现象.

目前, 国内外对于共轴旋翼、纵列旋翼的气动及流场特性研究相对较多.谭剑锋等[1]采用非定常面源法和黏性涡粒子法研究了共轴刚性双旋翼非定常气动特性.文献[2-8]采用CFD方法对共轴旋翼的流场及气动特性进行了研究, 文献[9-13]采用实验方法对共轴旋翼气动特性进行了研究, Coleman[14]对各国在共轴旋翼的气动方面的实验研究进行了介绍.黄水林等[15-16]采用实验和数值方法研究了纵列旋翼的流场及气动特性.而对于交叉旋翼气动特性方面的研究较少, 文献[17]对交叉旋翼总体设计和测试进行了介绍.

交叉旋翼气动效率较高, 但相互之间存在气动干扰, 同时交叉旋翼之间的交叉角度受结构限制, 因此, 分析交叉旋翼之间的气动干扰作用, 确定合适的交叉角度对于指导工程研制具有重要意义.

因此, 本文首先建立了适合于交叉旋翼的非定常干扰流场模拟的数值方法, 采用该方法模拟了交叉旋翼在几种不同状态下的流场特性, 并与单旋翼、共轴旋翼的气动特性进行了对比.

1 数值计算方法

流场控制方程采用三维非定常Reynolds平均Navier-Stokes(RANS)方程, 积分形式为

式中,V为控制体体积;Q为守恒变量矢量;σ为控制体表面积;F为通过表面σ的净通量矢量, 包含黏性项和无黏项;n为表面σ的单位外法向矢量.

采用有限体积法对控制方程进行空间离散, 时间采用2阶隐式格式.湍流模型采用有曲率修正的两方程SSTk-ω模型.

采用动态嵌套网格方法模拟旋翼运动, 其中背景网格采用非结构网格, 并在旋翼附近局部加密, 桨叶网格采用C-H型网格, 边界层网格第1层网格厚度为桨叶弦长c的5×10-5, 桨叶网格与背景网格之间以及桨叶网格之间通过交界面交换流场信息.流场边界采用远场边界条件.

文中旋翼拉力系数CT、扭矩系数CQ、悬停效率η定义如下

式中,T为旋翼拉力,ρ为空气密度,Ω为旋翼转速,R为旋翼半径,Q为旋翼扭矩.

2 数值方法的验证

交叉旋翼方面的实验数据较少, 共轴旋翼与交叉旋翼同样具有强烈的气动干扰, 因此采用共轴旋翼实验数据对计算方法进行验证.

式中：i1、i3分别为流经阀1和阀3的瞬时电流，其中：i1=ik，i3=Id-ik，vb-va=vab。将其代入式(3)中并对等式两边积分，得到下式：

共轴旋翼悬停状态验证算例采用文献[14]中的共轴旋翼悬停实验结果.旋翼半径R=0.38 m, 桨叶弦长c=0.06 m, 翼型为NACA0012, 上下旋翼各两片桨叶, 间距h=0.1 m, 旋翼转速Ω=3 100 r/min.图1为共轴旋翼网格, 图2为计算值与实验值对比.

图1 共轴旋翼网格

从图2可以看出, 上下旋翼CT-CQ的计算值与实验值符合性较好, 其中拉力系数计算值相比实验值略小.

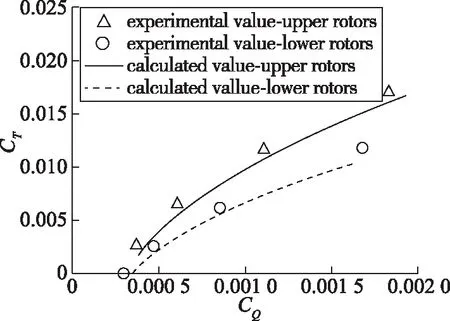
图2 共轴旋翼CT-CQ对比

3 交叉旋翼气动计算结果分析

交叉旋翼桨叶模型采用文献[18]的旋翼桨叶模型, 旋翼直径D=2.286 m, 旋翼桨叶数为两片, 桨叶弦长c=0.190 5 m, 桨叶翼型为NACA0012翼型, 桨叶为平直桨叶, 无扭转.拟定标准状态两幅旋翼的中心距离L=0.3R, 旋转轴夹角γ=24°, 旋翼锥度角β=3°, 总距角θ=5°, 转速Ω=1 750 rpm, 两幅旋翼分别绕各自局部坐标系旋转轴旋转, 旋翼桨叶初始交叉角为θjx=90°, 见图3.两幅旋翼旋转方向相反, 从上向下看, 旋翼1逆时针旋转, 旋翼2顺时针旋翼.

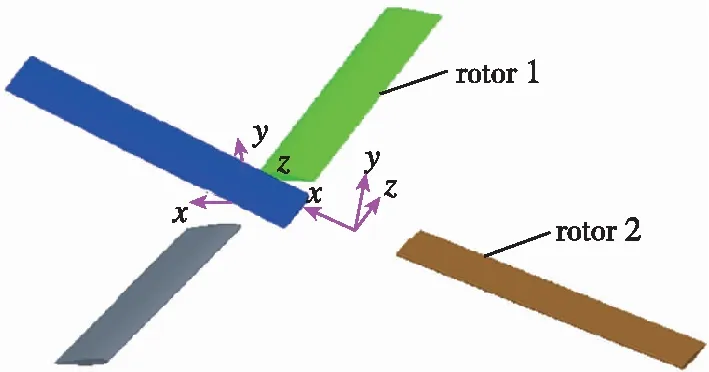
图3 交叉旋翼示意图

交叉旋翼计算网格见图4, 与单旋翼和固定翼网格不同, 由于旋翼距离较近, 交叉旋翼网格不仅与背景网格嵌套, 旋翼桨叶网格之间也相互嵌套.

3.1 标准状态计算分析

标准状态旋翼1和旋翼2拉力系数、扭矩系数随方位角变化见图5, 图中方位角以旋翼1初始位置为0°.

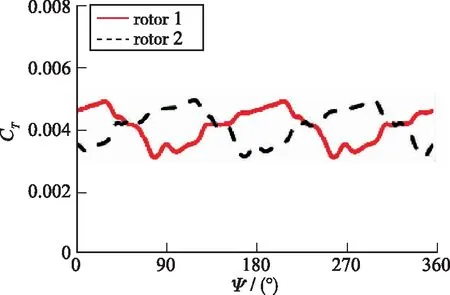
(a)Thrust coefficients

从图5可以看出, 单套旋翼拉力和扭矩系数以180°为一个周期变化, 旋翼1拉力系数在方位角Ψ=30°/210°附近达到最大值, 在方位角Ψ=90°/270°附近达到最小值, 旋翼2相比旋翼1延迟90°方位角.

图6所示为旋翼1桨叶在不同方位角时桨叶载荷分布情况.从图中可以看出, 由于旋翼之间的气动干扰, 0.9R以内180°方位角处桨叶剖面载荷明显大于90°和270°方位角处桨叶剖面载荷, 0°方位角处桨叶剖面载荷在0.6R以内明显小于其余3处方位角处的桨叶剖面载荷, 0.6R～0.9R之间则大于90°和270°方位角处桨叶剖面载荷.

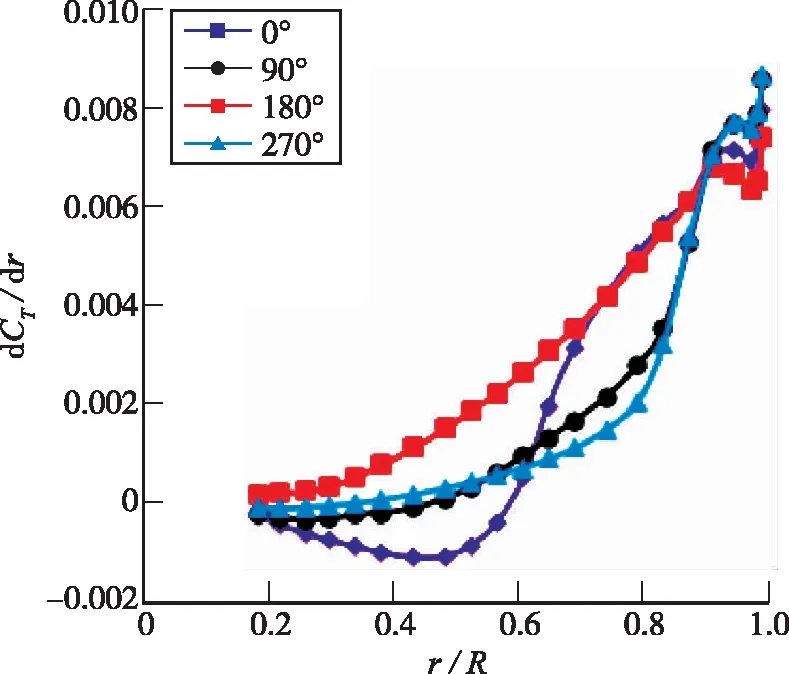
图6 不同方位角处桨叶展向剖面载荷分布

图7给出了旋翼1方位角Ψ=0°时的交叉旋翼流场Q等值面图, 其中7(a)为整体视图, 7(b)为侧视图.图8给出了x=0 m截面的涡量云图.

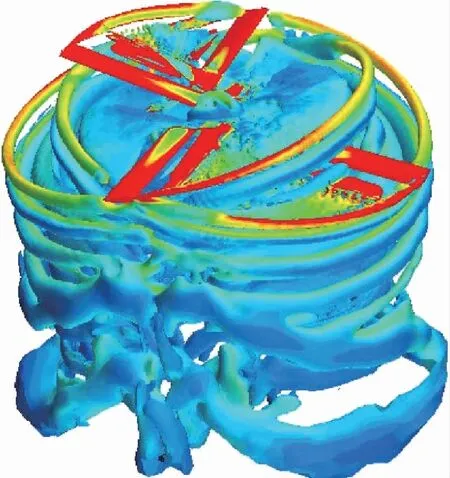
(a)Isometric view

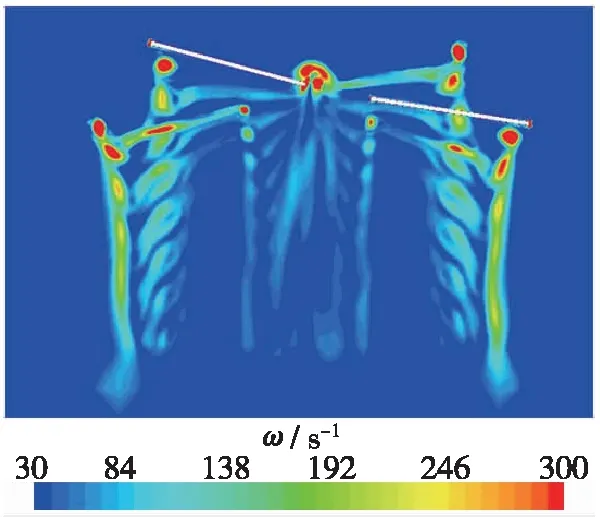
图8 截面涡量云图(x=0 m)

从图7，8可以看出, 悬停状态的交叉旋翼流场存在复杂的桨-涡干扰和涡-涡干扰现象.从图7可以看出, 旋翼1和旋翼2的桨尖涡各有一部分处于对方流场范围内, 并在方位角90°/270°附近相交, 两幅旋翼在方位角90°/270°附近穿过对方的桨尖涡.两套旋翼的流场相互影响, 桨尖涡在相交后形状发生了较大变化, 桨尖涡尺寸增大且涡量强度迅速减弱.总体上看, 外侧桨尖涡首先向内收缩,然后近似直线向下, 内侧桨尖涡收缩或扩张不明显, 呈现近似直线向下的状态.

图9为旋翼1在方位角为0°时x=0截面的桨尖涡位置, 图中采用的坐标系为旋翼1局部坐标系, 坐标原点为旋翼1旋转中心,y轴为旋翼1旋转轴.

图9 旋翼桨尖涡涡核位置

从图9可以看出受旋翼2流场影响, 旋翼1桨尖涡位置左右不对称.位于旋翼2流场内的旋翼1左侧桨尖涡向内收缩, 位于旋翼2流场外的旋翼1右侧桨尖涡先向内收缩然后向外扩张, 同时右侧桨尖涡向下运动速度大于左侧桨尖涡.旋翼2桨尖涡位置变化特点与旋翼1桨尖涡相似.

3.2 不同旋翼中心间距计算分析

旋翼交叉角度保持θjx=24°不变, 改变两幅旋翼中心间距.图10为交叉旋翼气动特性随旋翼中心间距变化趋势, 可以看出随着旋翼中心间距增大, 交叉旋翼拉力系数、扭矩系数均呈现增大, 但交叉旋翼扭矩系数增量较拉力系数增量小, 因此, 交叉旋翼悬停效率随着旋翼中心间距增大而增大.这主要是由于随着旋翼中心间距增大, 两幅旋翼之间的相互干扰逐渐减弱.

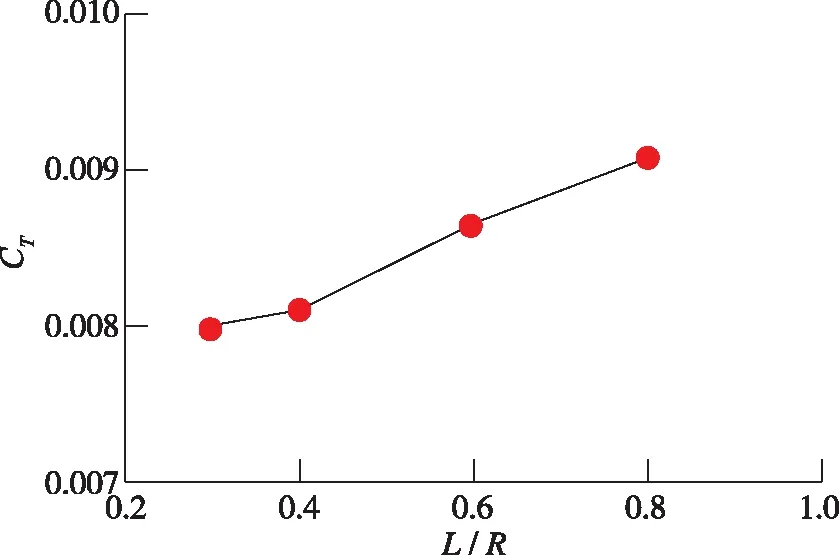
(a)Thrust coefficient

图11，12分别为旋翼1处于0°方位角时x=0截面和y=-0.5R截面处诱导速度分布.从图中可以看出,L/R=0.3时旋翼之间的气动干扰更为明显, 旋翼之间诱导速度叠加,L/R=0.3旋翼诱导速度明显增大, 导致桨叶迎角减小.L/R=0.8时, 旋翼中心距离较远, 旋翼气动干扰较弱, 旋翼诱导速度相对较小.同时, 从图11(a)可以看到, 旋翼1处于0°方位角处, 桨叶0.6R以内处于旋翼2诱导速度影响区域, 导致桨叶截面迎角减小, 升力降低, 而0.6R以外则不受旋翼2诱导速度影响, 升力恢复正常, 和图6所示结果一致.

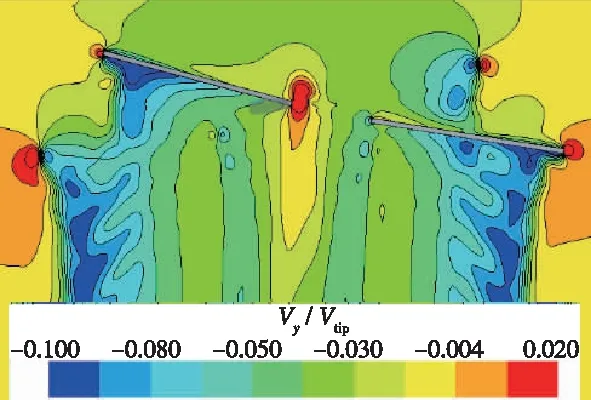
(a)L/R=0.3

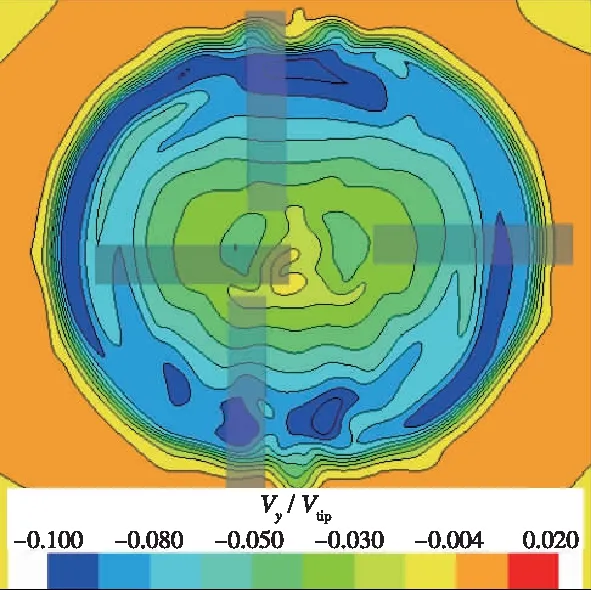
(a)L/R=0.3

3.3 不同交叉角度计算分析

两幅旋翼旋转中心间距保持L=0.3R不变, 改变旋翼旋转轴交叉角度.交叉旋翼气动特性随交叉角度变化见图13.可以看出, 在一定角度范围内, 交叉旋翼拉力系数、扭矩系数及悬停效率随交叉角度变化较小.

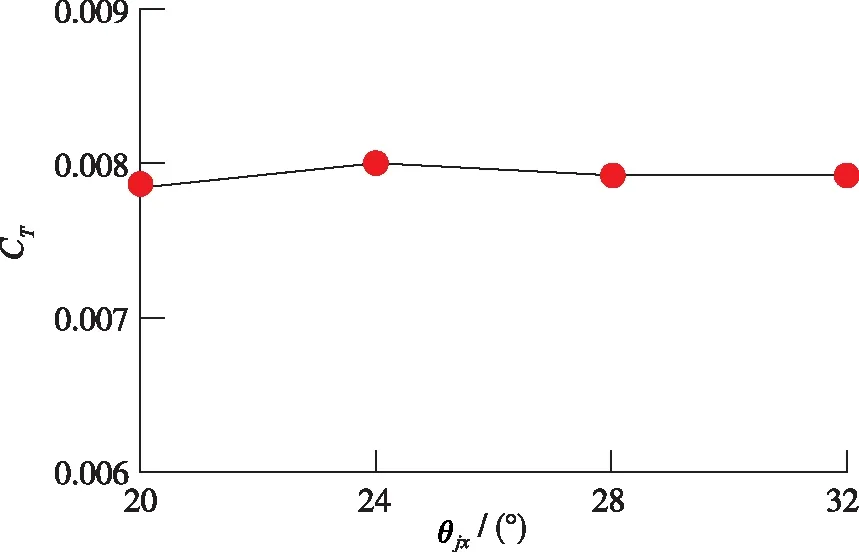
(a)Thrust coefficient

图14，15分别为旋翼1处于0°方位角时x=0截面和y=-0.5R截面处诱导速度分布.从图中可以看出,θjx=24°和θjx=32°分别在x=0和y=-0.5R诱导速度分布基本一致.θjx=32°分别相比θjx=24°交叉角度较大, 桨尖距离相对较远, 因此θjx=32°时旋翼诱导速度相对略小.同时θjx=32°旋翼拉力垂向分量相比θjx=24°旋翼拉力垂向分量略小, 共同作用结果是θjx=24°和θjx=32°时的交叉旋翼拉力基本一致.

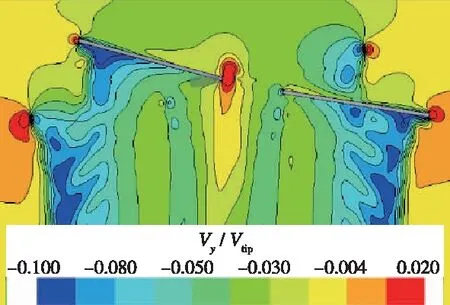
(a)θjx=24°

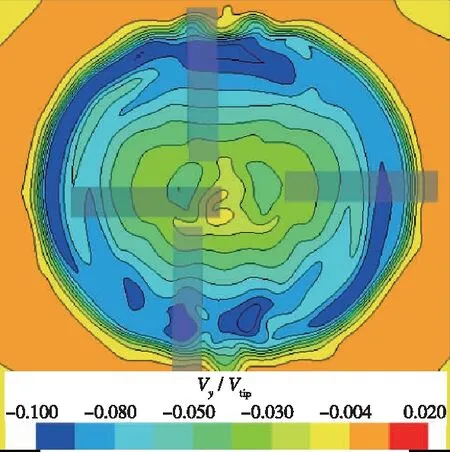
(a)θjx=24°

3.4 和其他类型旋翼气动特性对比

图16为不同类型旋翼气动性能计算结果对比.交叉旋翼和共轴旋翼、单旋翼均为4片桨叶, 旋翼总距角θ分别为5°和10°, 旋翼转速Ω均为1 750 r/min.其中, 交叉旋翼的旋翼中心间距L=0.3R, 交叉角度γ=24°; 共轴旋翼上下旋翼中心间距h=0.2R.

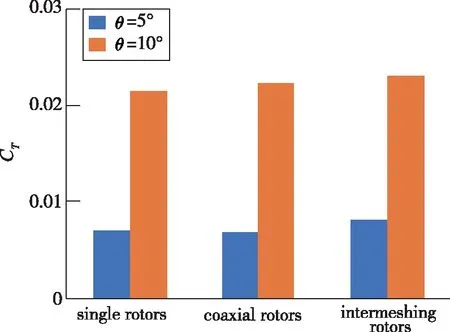
(a)Thrust coefficient

从图16可以看出, 交叉旋翼的拉力系数和悬停效率均大于相同总距角下单旋翼和共轴旋翼的拉力系数和悬停效率, 其中, 总距角θ=5°时拉力系数增大约15%, 悬停效率高6%～8%, 总距角θ=10°时拉力系数增大5%, 悬停效率高3%～6%.

4 结论

本文使用动态嵌套网格方法计算模拟了交叉旋翼的流场特征, 分析了交叉旋翼拉力与悬停效率随旋翼交叉角和中心距的变化规律.本文计算分析结果对交叉旋翼工程设计具有指导意义.具体结论如下:

(1)相同交叉角度下, 随着旋翼中心间距增大, 交叉旋翼两幅旋翼的干扰减弱, 交叉旋翼拉力系数和悬停效率有增加趋势; 相同旋翼中心间距下, 交叉旋翼拉力系数和悬停效率随交叉角度变化较小.

(2)交叉旋翼的桨尖涡在左旋翼方位角90°-右旋翼方位角270°附近相交并相互干扰, 桨尖涡尺寸变大, 涡量强度迅速减弱.同时, 单套桨尖涡的位置相对旋转轴左右不对称, 位于外侧桨尖涡向下运动速度大于内侧桨尖涡.

(3)相同旋翼半径、总距角和桨叶数量下, 交叉旋翼悬停效率相比单旋翼和共轴旋翼高 3%～8%.