基于转捩SST模型凸起圆柱绕流数值研究

吕代龙, 陈少松, 周 航, 徐一航

(南京理工大学能源与动力工程学院, 江苏南京 210018)

引 言

圆柱绕流是钝体绕流的重要研究案例, 是流体力学的经典问题.圆柱绕流问题是研究流动分离、涡流和涡脱落的重要基础, 在航空航天、船舶海洋以及兵器科学等领域有着重要的工程应用价值, 例如弹箭表面的电缆罩会引起流动分离, 使弹箭产生侧向力, 该问题可以简化为带有局部凸起的圆柱绕流问题.

圆柱绕流问题在早期的研究过程中局限性大, 研究的成果也相对简单, 大多以模型实验研究为主.国内外许多学者围绕圆柱绕流问题做了大量研究工作, 总结了不同Reynolds数下圆柱绕流的气动特性及变化规律.Aguirre-López等[1]采用直接数值模拟(direct numerical simulation, DNS)方法对Re=1.46×105带凸起的圆柱绕流问题进行了数值模拟, 得到了对圆柱气动特性影响最大的凸起位置.但是对于高Reynolds数下带凸起的圆柱绕流近壁面流动特征、涡的产生与脱离及流动机理等方面的研究相对较少, 对流动过程中边界层转捩的影响也很少关注.

边界层转捩现象是流体力学研究中一个难点问题, 是流体从层流到湍流状态的过渡阶段.尽管关于边界层转捩的基础理论和发生机理仍在研究发展中, 但其在工程实践应用中的重要性日益突出.而对于带有电缆罩的弹箭, 当电缆罩处于弹箭的非对称位置(如弹箭的侧面), 弹箭气动特性的不对称便会使弹箭产生侧向力, 这种现象在大攻角状态下更为明显.因此准确预测转捩点的位置、以及壁面的流动分离可以改善弹箭气动特性.

1 数值计算方法

1.1 转捩动量厚度Reynolds数输运方程

转捩动量厚度Reynolds数是转捩起始点的决定因素, 其输运方程为[11]

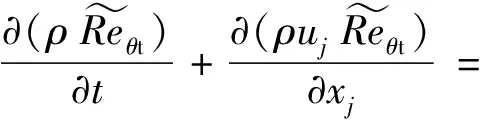
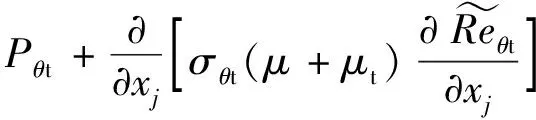
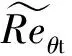
输运方程的生成项为

式中,cθt为常数;Fθt为开关函数, 该函数的值从边界层内部到外部由1逐渐变为0;Reθt为当地转捩Reynolds数, 该变量由来流湍流度Tu和压力梯度参数λθ拟合的经验公式得到.

1.2 间歇因子输运方程

边界层的转捩、湍流模型中的涡黏性系数等均由间歇因子控制, 其输运方程为[6]

式中,Pγ为生成项,Dγ为耗散项,γ为间歇因子.

1.3 SST k-ω湍流模型

SSTk-ω湍流模型的输运方程如下[13]

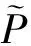
2 数值模拟条件及网格

2.1 数值模拟条件

本文研究的是来流速度U∞沿x轴正方向流向直径为D的二维带凸起的圆柱绕流问题, 如图1所示.图中θ为圆柱表面的方位角, 当θ=45°时, 圆柱表面上带凸起.分别取来流Re=1.4×105(亚临界区)，2×105，5×105(临界区)，1×106(超临界区), 根据实验条件选择来流的湍流强度为0.8%.

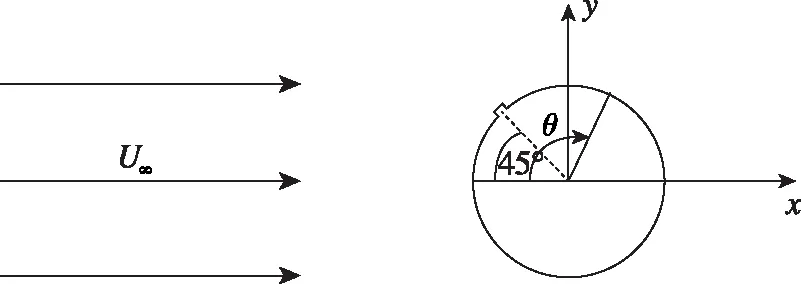
图1 流动示意图

时均阻力系数CD, Strouhal数St, 时均摩擦力系数Cf和时均压力系数Cp分别可由下列各式确定

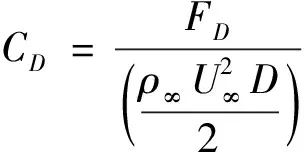
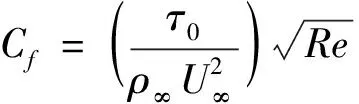
式中,FD为圆柱受到的时均阻力,f为涡脱落的频率,τ0为壁面剪切应力.

2.2 计算网格及边界条件

如图2所示, 采用尺寸为55D(来流方向)×40D(横流方向)的矩形区域作为计算域, 计算域上下边界和计算域左边界与圆柱中心的距离均为20D, 计算域右边界与圆柱中心的距离为35D.该尺寸保证了计算域足够大, 可有效避免边界对流场产生影响.物面法向第1层网格高度由y+～1确定.图3为圆柱表面附近网格的示意图.

图2 整个计算域网格示意图

图3 圆柱表面附近网格示意图

计算边界条件定义如下: 计算域的左边界为速度入口边界条件, 在此边界上指定均匀流速为u=U∞且v=0, 其中u和v分别是x和y方向上的速度分量; 圆柱表面采用壁面无滑移边界条件, 即u=v=0; 计算域的上下边界采用对称边界条件; 在计算域的右边界选用流动出口边界条件.

3 数值模拟结果

3.1 亚临界区数值模拟结果分析

表1给出了Re=1.4×105时, 通过数值模拟计算得到的二维带凸起圆柱的时均阻力系数CD和Str-ouhal数St的值, 也给出了Schewe[11]和Cantwell[14]通过实验测得的结果及苑明顺[10]数值模拟计算结果.对比表1中CD和St值, 可以看到所得结果与实验测得的结果基本符合, 说明在亚临界区采用转捩 SST模型能够很好地模拟二维圆柱绕流问题.

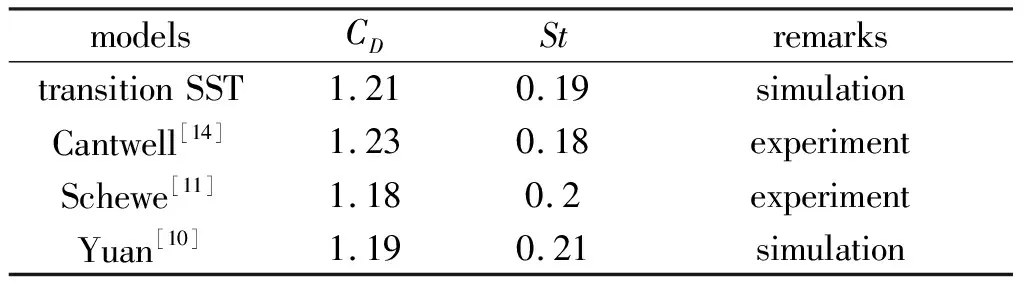
表1 亚临界区二维圆柱时CD和St数值模拟计算结果

图4给出了Re=1.4×105时通过转捩 SST与LES模拟得到的二维圆柱上下表面的时均压力系数Cp的分布曲线, 与Aguirre-López 等[1]通过DNS 模拟得到的结果进行对比可以看出: 与LES相比, 圆柱表面Cp的数值模拟结果与DNS得到的结果吻合较好, 在θ=40°～320°范围内, 上表面的Cp值小于下表面, 同样从图5压力云图可以看出, 圆柱上表面的压力小于下表面的压力, 这是由于在上表面凸起位置的前后产生了3个反向旋转的漩涡, 形成了背风面低压区, 如图6所示.同时由于涡的存在, 使涡上方流体的流通通道变窄, 造成流动速度增大、压强降低, 而在边界层内, 沿物体表面的法线方向压强保持不变, 即等于外边界处自由流的压强致使上表面的压强相对于下表面较低.

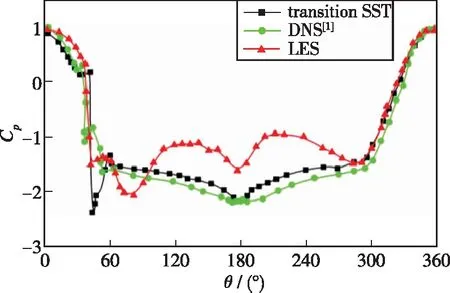
图4 亚临界区圆柱表面时均压力系数Cp分布曲线

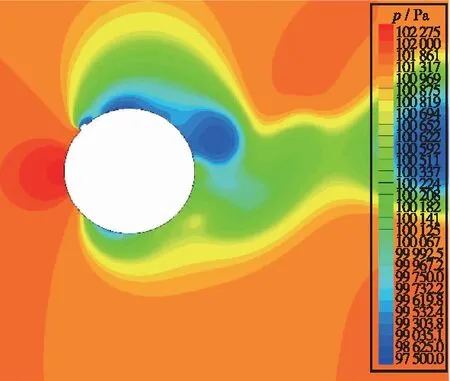
图5 亚临界圆柱表面压力云图

图6 漩涡流线图

图7给出了Re=1.4×105时通过数值模拟得到的二维圆柱上下表面的时均摩擦力系数Cf的分布曲线, 与Aguirre-López等[1]通过DDES方法得到的结果进行对比.由图4, 7可知, 转捩 SST模型能够相对准确地模拟圆柱绕流背风面压力和摩擦力的变化情况, 与DNS得到的结果相差不大.

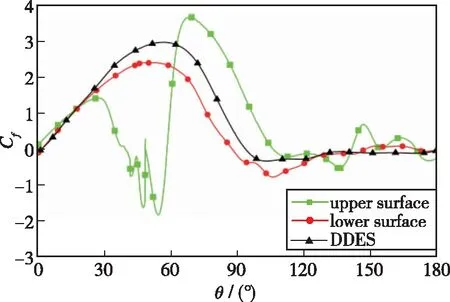
图7 亚临界圆柱表面时均摩擦力系数Cf分布曲线

从图7可以看出, 采用转捩 SST模型模拟得到的下表面计算结果在θ=88°时Cf由正变为负, 这表明此位置发生了流动分离现象; 而计算结果在θ=90°～130°范围内与DDES方法得到的不同变化的原因, 是由于流动处于亚临界区向临界区的过渡阶段, 流动分离之后有一个分离再附的趋势, 即有一个形成分离泡的趋势.上表面在θ=38°处Cf的正负符号发生了变化, 这表明在凸起的影响下, 流动在θ=38°处发生了流动分离; 在θ=38°～60°范围内Cf处在负区间, 这是由于凸起的影响, 流动在凸起前后流动产生了漩涡; 在θ=60°～106°范围内Cf随θ先增大后减小, 在θ=73°时Cf达到最大值, 说明流动分离之后在此范围内再附; 而在θ=106°处Cf的正负符号又发生了改变, 流动在这个位置又产生流动分离现象; 此处之后, 与下表面相比, 上表面的Cf围绕Cf=0上下震荡, 是因为表面凸起的影响, 流动分离后再附产生了分离泡现象.

对于圆柱绕流问题, 尾迹区的近壁区流动特征主要是分离与局部二次分离产生不同尺度漩涡的合并、成对、分叉等强烈的相互作用, 漩涡脱落的过程实际上是多个涡间及与剪切层相互作用的结果.在高Reynolds数下, 漩涡只要强度足够大或者距离壁面足够近, 二维或三维漩涡皆可在近壁区诱导产生局部分离, 形成新的漩涡.

图8给出了凸起圆柱在背风面尾迹区流动的一个周期内的变化过程.t1时刻尾迹区圆柱上表面附近产生的漩涡距离壁面非常近, 由于其诱导作用, 使尾迹区圆柱下表面在t2时刻发生了流动分离, 产生了新的漩涡, 且在尾迹区上表面附近的漩涡随着时间的发展逐渐变大并沿流向向后发展, 由于其与尾迹区下表面附近的剪切层相互作用, 在t3时刻尾迹区圆柱下表面附近产生了3个小漩涡, 并且这3个小漩涡与之前上表面附近产生的小漩涡由于旋向以及来流的影响开始合并, 在t6时刻完成合并, 成为一个正向旋转的漩涡.同时, 由于涡间以及来流的影响, 在t6时刻形成的正向漩涡和之前由诱导作用产生局部分离形成的漩涡开始合并, 在t7时刻完成合并, 发展成为一个大的分离涡, 然后随着时间的推移发生漩涡脱落.

图8 临界区圆柱尾迹区一个周期的变化过程

综上所述, 转捩 SST模型对流动分离和压力梯度等因素敏感, 能很好地模拟二维凸起圆柱表面的压力、摩擦力变化以及尾迹近壁区的流动分离等流动特性.

3.2 临界区数值模拟结果分析

图9为流动处于Re=2×105和Re=5×105时数值模拟计算所得的圆柱上下表面时均压力系数Cp分布曲线.可以看出, 两个Reynolds数下Cp的分布曲线趋势大致相同,Cp的值都是逐渐减小, 这也符合其变化规律; 对比两个Reynolds数下圆柱表面的分布曲线, 由于凸起的影响, 在凸起附近的压力系数发生突变, 之后的压力系数逐渐与光滑表面的相近.与亚临界区流动相同, 临界区的圆柱上表面时均压力系数Cp与下表面相比, 也要稍小, 其原因与亚临界区流动相同.

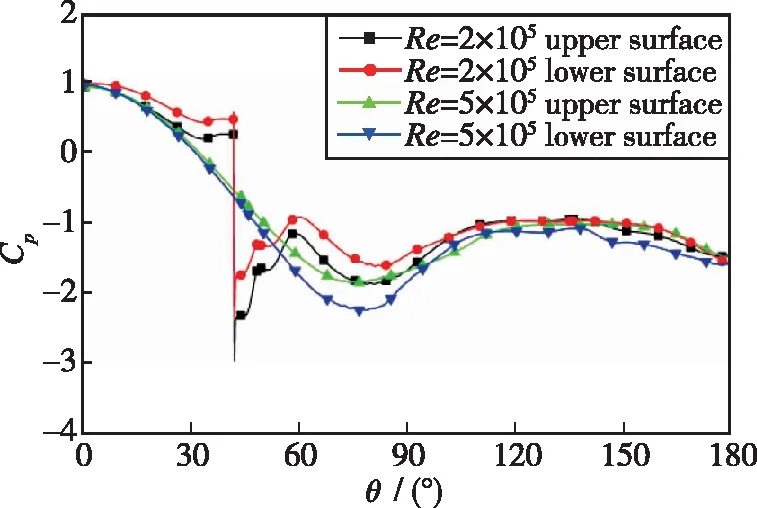
图9 临界区圆柱表面时均压力系数Cp分布曲线

图10为流动处于Re=2×105和Re=5×105时数值模拟计算得到的圆柱表面时均摩擦力系数Cf分布曲线, 可以看出, 数值模拟得出了圆柱表面时均摩擦力系数Cf突然增大又回落减小的过程, 也就是圆柱边界层的转捩过程.

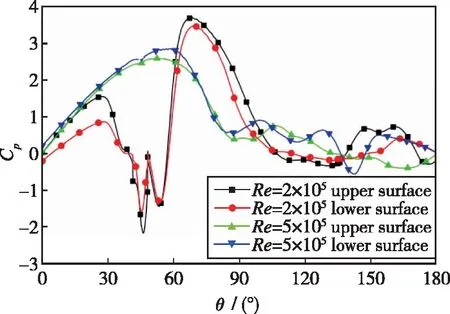
图10 临界区圆柱表面摩擦力系数Cf分布曲线

流动处于Re=5×105时下表面时均摩擦力系数Cf在圆柱下表面θ=130°～150°范围内由正变负再变正, 表明边界层内发生了流动分离和再附的过程, 产生了分离泡.Cf在圆柱上表面θ=30°～60°由正变负又变正, 这就表明由于凸起的影响, 边界层在此处发生了流动分离, 产生了漩涡现象; 之后Cf的值突然变大, 又回落减小, 这说明流动重新附于圆柱表面上; 在圆柱上表面θ=105°～146°时Cf由正变负又变正, 这就表明在边界层流动发生了分离和再附的过程, 即产生了分离泡.同时, 与流动处于亚临界区时上表面产生流动分离现象的位置大致相同.

图11为流动处于临界区时圆柱上表面附近流动区域的速度矢量图, 从左至右依次为a,b,c,d,e点.从a可以看出, 在此区域内流向圆柱上表面外法线方向的速度梯度逐渐变大, 使流向圆柱上表面剪切应力逐渐增大, 导致时均摩擦力系数Cf逐渐变大.

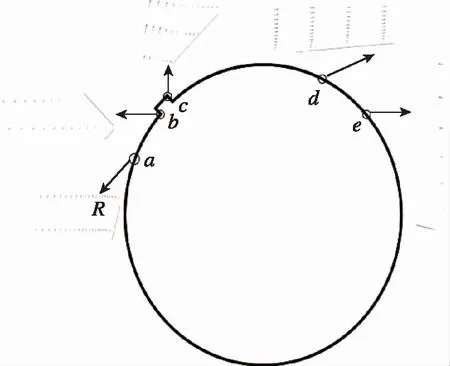
图11 临界区二维凸起圆柱速度矢量图

从b和c可以看出, 在圆柱上表面θ=30°～60°这个区域内沿流向圆柱上表面气流的速度梯度在逐渐减小, 速度矢量方向与来流方向先相同后相反再相同, 这就使得沿流向上表面时均摩擦力系数Cf逐渐减小, 最终由负又变正.

从d和e可以看出, 在此区域内圆柱上表面气流的速度矢量方向与来流方向先相同后相反再相同, 说明在流动发生了分离后再附, 形成了一个分离泡.

通过采用转捩 SST模型对临界区凸起圆柱绕流问题的计算分析, 可以看出, 气流在凸起前后形成了3个反向旋转的漩涡, 形成了背风面低压区, 之后随着上表面θ的增加, 气流先是发生了流动分离现象, 产生了分离泡, 然后发生了转捩, 并发生了流动分离.

3.3 不同Reynolds数下模拟结果对比

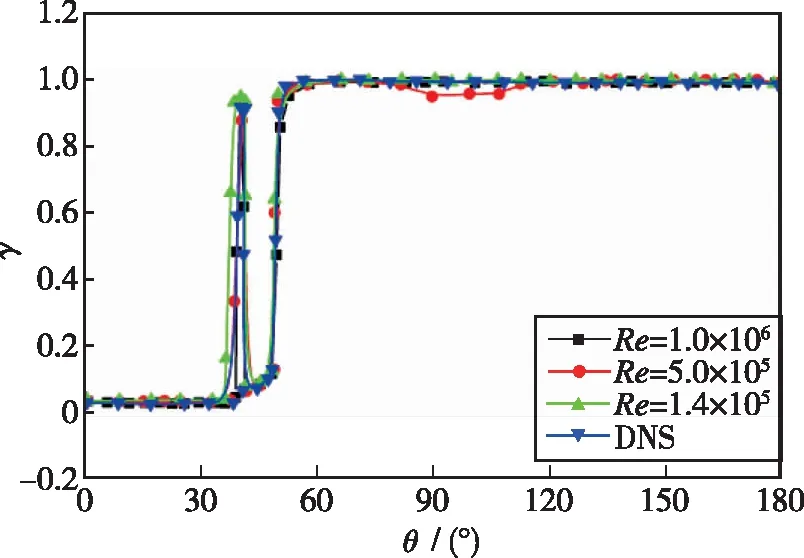
图12给出了在不同Reynolds数下得到的圆柱表面时均摩擦力系数Cf的分布曲线, 图13为不同Reynolds数下圆柱边界层的间歇因子γ的分布曲线, 与采用DNS模拟得到的γ的分布曲线吻合较好.

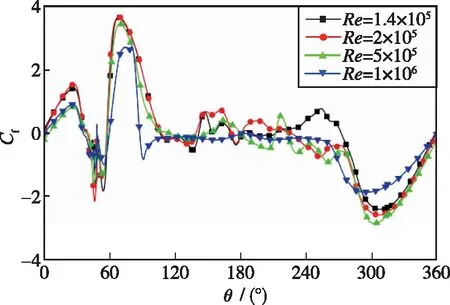
图12 不同Reynolds数下圆柱表面时均摩擦力系数Cf分布曲线

(a)Upper surface of cylinder

从图12可以看出, 在凸起前后, 圆柱上表面时均摩擦力Cf的符号为负, 这说明流体在此发生了流动分离, 产生了分离涡, 结合流场结构可以得出, 在凸起处形成了3个逆向旋转的小涡.同时随着Reynolds数的增加, 气流发生分离再附的位置逐渐向前.

当流动处于Re=2×105时, 在圆柱上表面θ=50°处的时均摩擦力系数Cf先增大后减小, 且由图13(a)可得, 在此处边界层的间歇因子γ从0突变到1, 表明流动在θ=50°处发生了转捩.而在圆柱下表面, 转捩的位置在下表面θ=90°左右处, 明显比上表面的转捩位置滞后, 这表明凸起可以使流动转捩过程提前.从图13(b)可以看出, 当Re=5×105和Re=1×106时, 圆柱下表面边界层内发生了转捩过程, 其转捩点分别位于下表面θ=89°和θ=85°处, 说明当Reynolds数处于临界区和超临界区时, 随着Reynolds数的增加, 圆柱边界层转捩点的位置逐渐向来流方向移动.

综上所述, 对于不同Reynolds数下的圆柱表面, 气流会在圆柱表面凸起处产生3个反向旋转的小漩涡, 发生流动分离现象.同时圆柱上表面的凸起可以使气流的转捩提前发生, 并且随着Reynolds数的增加, 圆柱边界层转捩点的位置逐渐向后移动.

4 结论

本文采用转捩 SST模型对不同Reynolds数下的二维凸起圆柱绕流问题进行了数值模拟计算, 在Re=1.4×105时, 通过对圆柱表面时均压力系数、时均摩擦力系数和间歇因子等与DNS结果进行比较, 验证了转捩 SST模型在模拟圆柱绕流问题方面的准确性.之后采用该模型对不同Reynolds数下的凸起圆柱绕流问题进行了计算分析, 得到了不同Reynolds数下圆柱近壁区的流动特性和变化规律, 可以得到以下结论:

(1)当来流Reynolds数处于临界区时, 气流在圆柱上表面凸起处形成了3个反向旋转的漩涡, 并在之后随着θ的增大, 发生了流动分离和流动转捩现象.

(2)对于不同Reynolds数的来流, 圆柱上表面的凸起可以使气流发生转捩的位置提前, 并且随着Reynolds数的增加, 其转捩位置逐渐后移.

(3)上表面凸起位置的前后产生了3个反向旋转的漩涡, 形成了背风面低压区.同时, 由于涡的存在, 使涡上方流体的流通通道变窄, 造成其流速增大、压强降低, 从而导致圆柱产生升力, 随着来流Reynolds数的增大, 其升力逐渐变大.