边条翼后掠角对钝头细长旋成体非对称流动的影响

袁起航, 王延奎, 李 乾, 齐中阳

(1.北京航空航天大学航空科学与工程学院, 北京 100191; 2.北京航空航天大学宁波创新研究院先进飞行器与空天动力创新研究中心, 浙江宁波 315800)

引 言

随着现代战争中精确打击要求日益提高, 导弹的作用愈发明显[1-2].用于夺取制空权的空战中使用的空空导弹，由于其攻击目标特点而要求具有高机动性[3-4], 为保证高机动性能, 空空导弹通常在改变飞行方向时采用大迎角机动[5-6].目前空空导弹的弹身结构多为钝头细长旋成体, 在弹身侧面不同位置安装弹翼、舵面, 各组翼面联合操纵满足导弹的机动需求.当导弹大迎角飞行时, 弹身对弹翼等控制面存在阻挡作用, 导致弹翼的控制效率大幅度降低, 因而高效飞行控制成为导弹大迎角机动的基本要求.此外, 在大迎角飞行时导弹周围往往伴随着大范围的分离流动, 出现由分离面卷起的旋涡[7-10].研究表明, 大迎角下细长体表面的流动会逐步演化为非对称流动(见图 1), 这种非对称流动通常不确定且不可预测, 导弹在这种流动的诱导下产生方向不确定的侧向力, 造成了导弹在大迎角飞行时受到的控制不可靠, 极易导致导弹射击任务失败[11].

图1 钝头细长旋成体大迎角非对称流动

前人开展了大量关于细长旋成体大迎角非对称绕流的研究.20世纪50年代初, Allen等在细长体大迎角无侧滑绕流流场显示实验中首先观察到细长体非对称背涡的现象[12], 并指出产生侧向力的原因为细长体的非对称背涡结构.20世纪70年代后, 对飞行器大迎角机动性能的需求使得细长体大迎角绕流非对称性问题成为空气动力学界研究的热点[13-16].由于绕流主控因素的多样性, 研究很难获得可重复的实验结果, 大量的风洞试验结果表明, 大迎角绕流对各种模型头部细微的干扰(细微几何偏差、表面粗糙度等)非常敏感, 其中模型头部极小的加工偏差都可以成为非对称流动的来源[15,17-21].邓学蓥等[17-18]、Hartwich等[20]、马宝峰[22]通过在模型头部施加固定位置的颗粒扰动, 得到了确定的非对称流动现象, 并且确定了非对称流动结构随扰动颗粒的位置不同呈现出不同的稳态流动形式, 即模型的非对称流动受到头部扰动颗粒的主控[23-27].

目前, 国内外针对细长体大迎角非对称流动的研究多集中在尖头细长体模型, 而对钝头细长体, 尤其是带有弹翼钝头细长体绕流的研究极少[28].本文在钝头细长体模型的头部设置人工微扰动, 产生确定的非对称流场, 在头部附近安装边条翼, 通过改变边条翼前缘后掠角, 测量各截面的物面压力, 积分得到不同边条翼前缘后掠角条件下各截面时均侧向力系数, 结合粒子图像测速实验获得空间流场分布变化情况, 分析了边条翼后掠角对绕模型非对称流动的影响及原因.

1 模型与研究方法

本文实验在北京航空航天大学D4低速回流式风洞中完成, 风洞实验段截面尺寸为1.5 m ×1.5 m, 自由来流的湍流度小于0.08%.用于实验的钝头细长旋成体模型尺寸、坐标系定义及测压截面位置如图 2所示, 图中长度单位为mm.模型总长为1 240 mm, 等直段直径D=100 mm, 头部钝度为0.82, 在距模型头部顶点160 mm处安装了一组边条翼, 每个边条翼弦向长度为110 mm, 展向长度为30 mm.模型共有3组可互换的边条翼, 各组边条翼的前缘后掠角χ分别为0°，30°，60°.模型头部表面附有颗粒人工微扰动以保证大迎角条件下实验结果的确定性[17-18,23-27].颗粒尺寸为直径Dp=0.8 mm(Dp/D=0.008), 人工微扰动的安装位置由模型头部子午角σ及周向角θp确定, 角度定义见图 2.本文实验中的人工微扰动周向角、子午角均唯一确定,θp=270°,σ=10°.测压模型表面沿x轴方向布置6个测压截面, 每个测压截面沿周向均布24个垂直于模型当地表面的测压孔, 各孔的周向位置由周向角θ确定.本文的测压实验中传感器的测量精度为满量程(1 psi)的0.10%.实验中的采样频率设置为50 Hz, 采样时间为12 s.实验中的自由来流条件均为Re=150 000(特征长度以模型等直段直径D计算), 模型的迎角为α=50°, 侧滑角为β=0°.

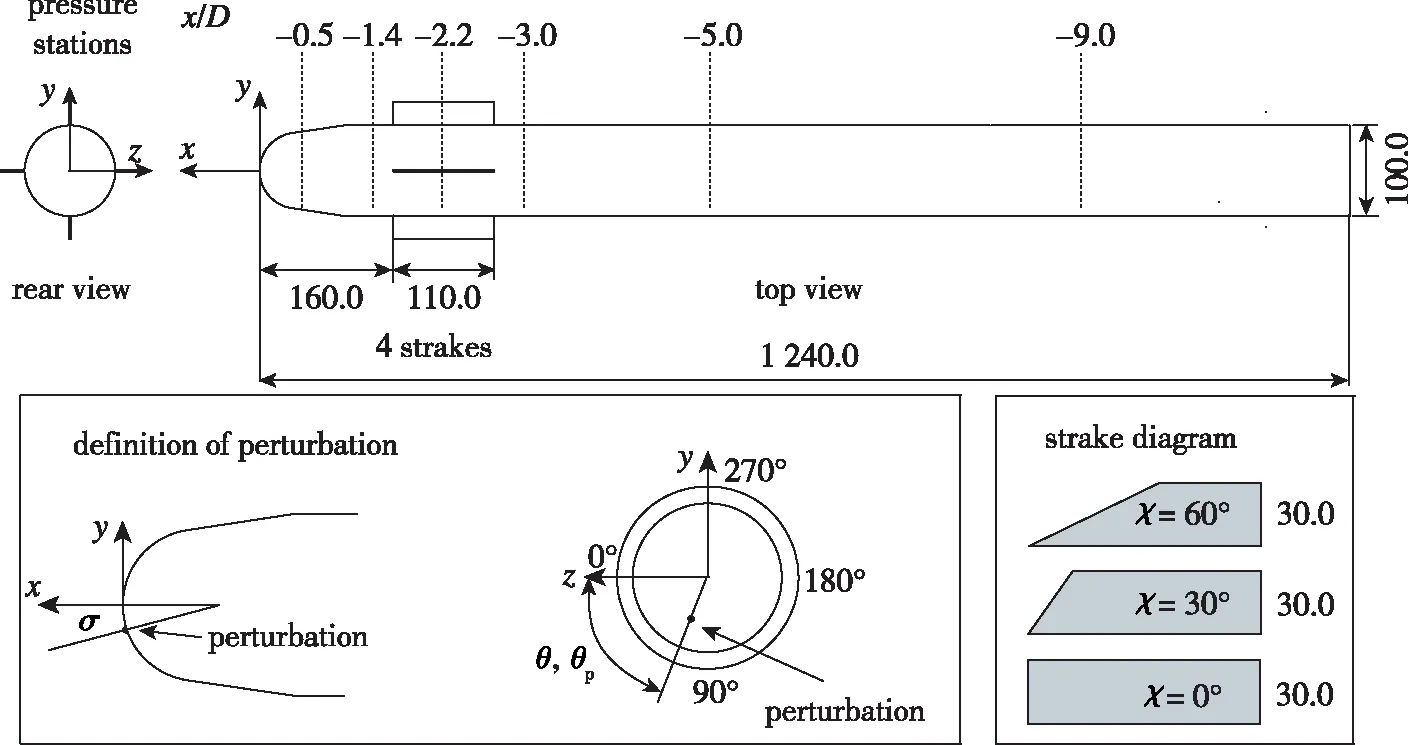
图2 实验模型示意图

粒子图像测速(particle image velocimetry, PIV)实验中片光与模型x轴垂直, 为使诊断窗口中的粒子数量达到最佳(各诊断窗口中粒子个数不小于10)[29], 激光在拍摄区域内的平均片光厚度调整为5 mm, 两束激光之间的时间间隔设置为30 μs.PIV实验采集频率为10 Hz, 采样点为200个.拍摄视场尺寸为350 mm×221 mm(3.5D×2.2D), CCD传感器像素为1 920 pix×1 200 pix, 即采集图像的分辨率为5.48 pix/mm, 互相关运算的最终诊断窗口尺寸为 64× 64, 窗口重叠率为50%, 最终矢量图中的每个矢量的尺寸为3.01 mm.除了x方向的涡量ωx=∂w/∂y-∂v/∂z分布以外, 本文还利用Q准则计算了涡量分布[30]

Q=-0.5[(∂v/∂y)2+(∂w/∂z)2]-(∂v/∂z)(∂w/∂y)

仅展示流场中Q>0的部分以排除涡量中剪切层对判断旋涡位置的干扰, 公式中的v,w分别表示y,z方向的速度分量.

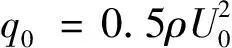
2 结果及分析

2.1 边条翼后掠角χ=0°

图3, 4分别为χ=0°条件下不同截面的时均压力系数与时均涡量分布, 其中仅保留涡量图中Q>0的部分.

图3 边条翼χ=0°条件下的各截面压力系数

从钝头细长旋成体头部开始, 受到人工微扰动的作用, 流动发生非对称分离形成前体非对称涡, 产生局部侧向力[24-27].在前体非对称涡向下游发展的过程中, 与边条涡之间产生复杂的诱导和耦合效应[28].在边条翼前缘产生的旋涡关于模型纵向对称面基本呈对称状态, 且其涡位比前体非对称涡更靠近钝头细长旋成体左、右两侧物面, 使得钝头细长旋成体前体非对称涡与边条涡之间的诱导和耦合绕流对钝头细长旋成体物面的非对称诱导作用减弱, 进而导致钝头细长旋成体截面侧向力减小.

在边条翼所在的3个截面(x/D=-1.8,-2.2,-2.6), 两片相邻边条翼之间的旋成体背风区物面上存在由边条翼与前体涡共同诱导产生的二次涡, 二次涡的强度较小且所在位置远离模型左、右两侧θ=90°，270°区域, 因此对截面侧向力的贡献较小.

2.2 边条翼后掠角χ≠ 0°

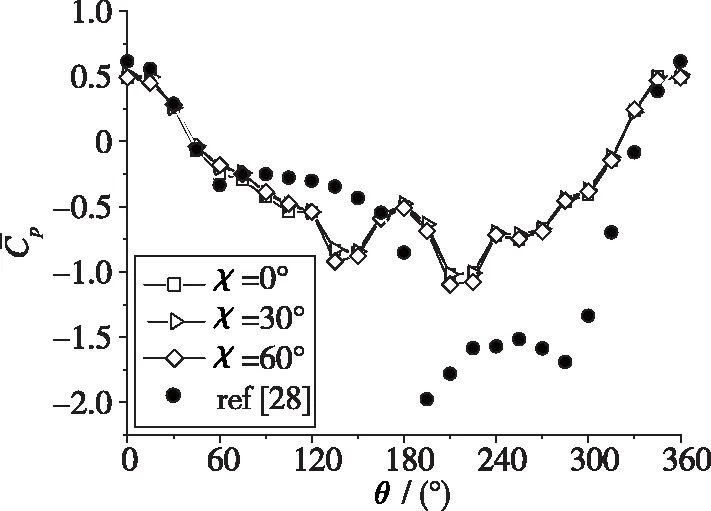
图 5所示为不同边条翼前缘后掠角条件下的模型截面侧向力沿体轴变化曲线, 图 5(a)中包括了未安装边条翼的钝头细长旋成体数据作为参考[28].图 5(b)清晰展示了3种不同边条翼后掠角条件下的截面侧向力系数, 特将图5(a)局部放大.

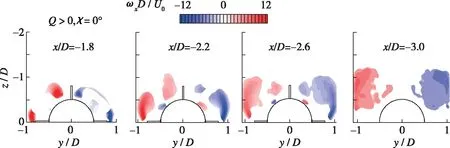
图4 边条翼χ=0°条件下的各截面涡量分布

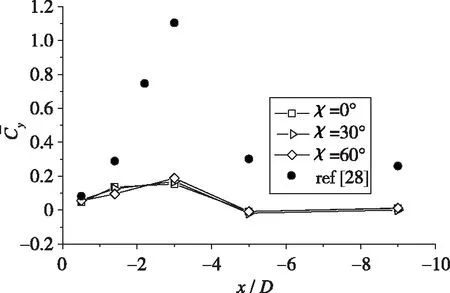
(a)Time-averaged sectional side-force coefficient of a slender body with and without strakes of different swept leading edges

在不同边条翼前缘后掠角的条件下, 侧向力系数沿模型体轴从前至后均呈现减幅类正弦曲线式变化.边条翼后掠角对侧向力系数的影响主要体现在边条翼上下游截面.侧向力系数随边条翼前缘后掠角的变化趋势: 在x/D=-1.4截面, 边条翼前缘后掠角越大, 截面侧向力系数越小; 在x/D=-3.0截面, 边条翼前缘后掠角越大, 截面侧向力系数越大.对于远离边条翼的下游截面, 后掠角对截面侧向力的影响极小.

图 6(a),(b)分别展示了边条翼上游x/D=-1.4截面的时均压力分布及各测压点对侧向力的贡献, 其中包括了未安装边条翼的钝头细长旋成体数据作为参考[28].迎风面(θ<90°及θ>270°)流动中, 边条翼前缘后掠角增大时, 相同周向位置的物面压力更低.随着边条翼前缘后掠角增大, 可能造成迎风面逆压梯度降低, 模型迎风面相同周向位置的速度更大、物面压力更低.

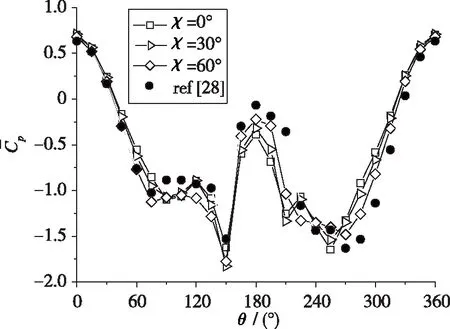
(a)Time-averaged pressure coefficient

模型背风面(90°<θ<270°), 由于人工微扰动位于θp=270°, 模型左侧为前体高涡, 右侧为前体低涡.前体高涡随前缘后掠角变大而分离提前, 如在χ=60°条件下流动在θ=90°附近发生分离, 另外两种边条翼发生分离的位置为θ=120°.前体低涡随前缘后掠角变大分离也提前, 如在χ=60°条件下在θ=240°发生流动分离, 而另外两种后掠角条件下分离发生在θ=225°.

在各测压点对侧向力的贡献中, 位于θ=0°，180°附近的测压点对侧向力贡献接近0, 而对侧向力贡献较大的位置是θ=90°，270°附近的测压点.随着后掠角的增大, 模型左侧受到的吸力逐渐增强而右侧逐渐减弱, 因此本截面模型受到的侧向力随着后掠角增大而减小.

为了观察对侧向力贡献最大的周向位置流场, 图 7展示了x/D=-1.8截面的时均涡量分布, 仅保留涡量分布图中Q>0的部分.可以看出, 一对边条涡位于对侧向力贡献最大的周向位置.

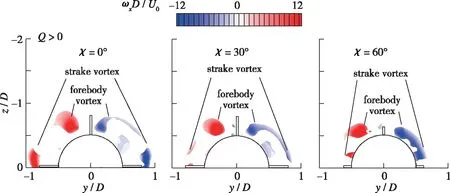
图7 x/D=-1.8截面时均涡量分布

图 8为x/D=-1.8截面的边条涡涡量最大值及最大值处的展向位置随后掠角变化.χ=0°边条翼诱导出一对边条涡对称分布于边条翼侧缘的背风面, 而前体非对称分离产生的旋涡位于模型背风区靠近θ=180° 处; 随着边条翼后掠角增大, 模型左右两侧的边条涡均靠近模型纵向对称面, 且边条涡位置基本对称, 同时边条涡涡量的最大值有下降趋势.

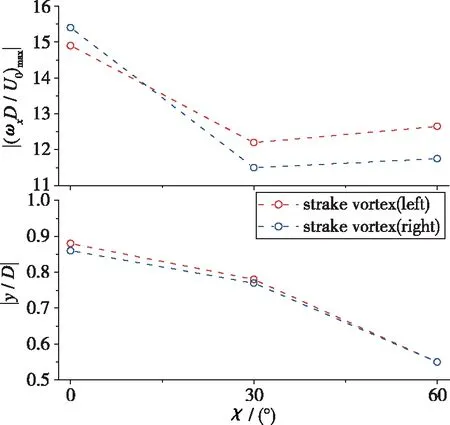
图8 x/D=-1.8截面边条涡的涡量最大值及对应展向位置随后掠角变化

随边条翼后掠角增大, 其产生的边条涡更靠近物面, 对物面流动的诱导作用增强, 由于其自身关于模型纵向对称面对称发展, 因此诱导物面流动使流动趋于对称化, 这一规律可以解释图 6在边条翼开始前的x/D=-1.4截面压力分布中χ=60°曲线θ=90°附近的吸力增大, 而θ=270°附近的吸力减小, 减弱了流动的非对称性, 以及图 5中x/D=-1.4 截面的截面侧向力系数随后掠角增大而减小.

图 9, 10展示了边条翼中点位置x/D=-2.2截面的时均压力分布及涡量分布, 其中包括了未安装边条翼的钝头细长旋成体数据作为参考[28].图 11为x/D=-2.6截面的涡量分布, 涡量仅保留涡量分布图中Q>0的部分.

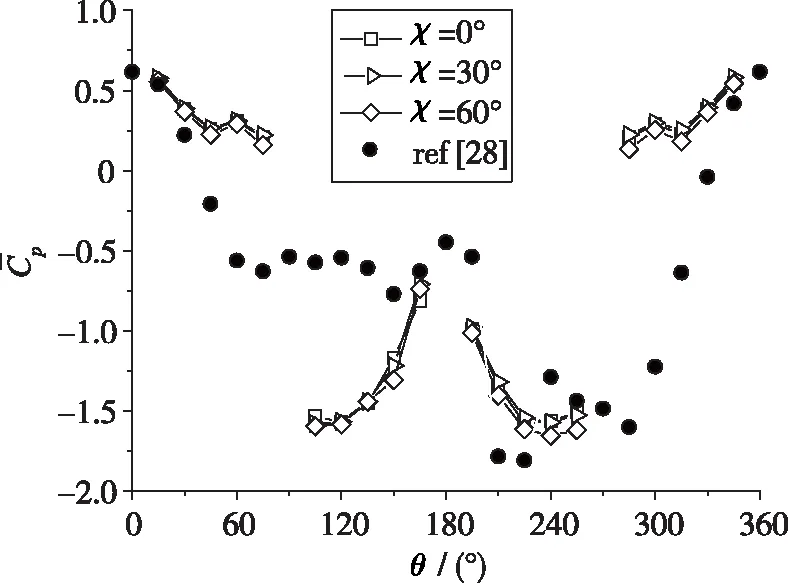
图9 x/D=-2.2截面时均压力系数

相比于上游截面,x/D=-2.2截面的3条压力分布曲线重合较好.随着边条翼后掠角增大, 本截面迎风面各点的压力均略下降, 说明在此过程中边条涡的诱导作用增强.从x/D=-2.2截面开始, 前体非对称涡与边条涡的空间位置逐渐接近.

图 11中的x/D=-2.6截面, 随着边条涡发展逐渐占据边条翼背风侧的大部分区域, 前体涡与边条涡继续接近, 左(或右)侧的前体涡与同侧边条涡之间相互诱导: 受前体涡影响, 边条涡出现了非对称现象; 受边条涡影响, 前体涡远离模型纵向对称面向边条涡靠近.边条翼后掠角越大, 这种相互诱导的作用越明显.

图 12(a),(b)分别是边条翼下游x/D=-3.0截面的时均压力分布及各测压点对截面侧向力的贡献, 其中包括了未安装边条翼的钝头细长旋成体数据作为参考[28].图 13为该截面的涡量分布, 仅保留涡量分布图中Q>0的部分.

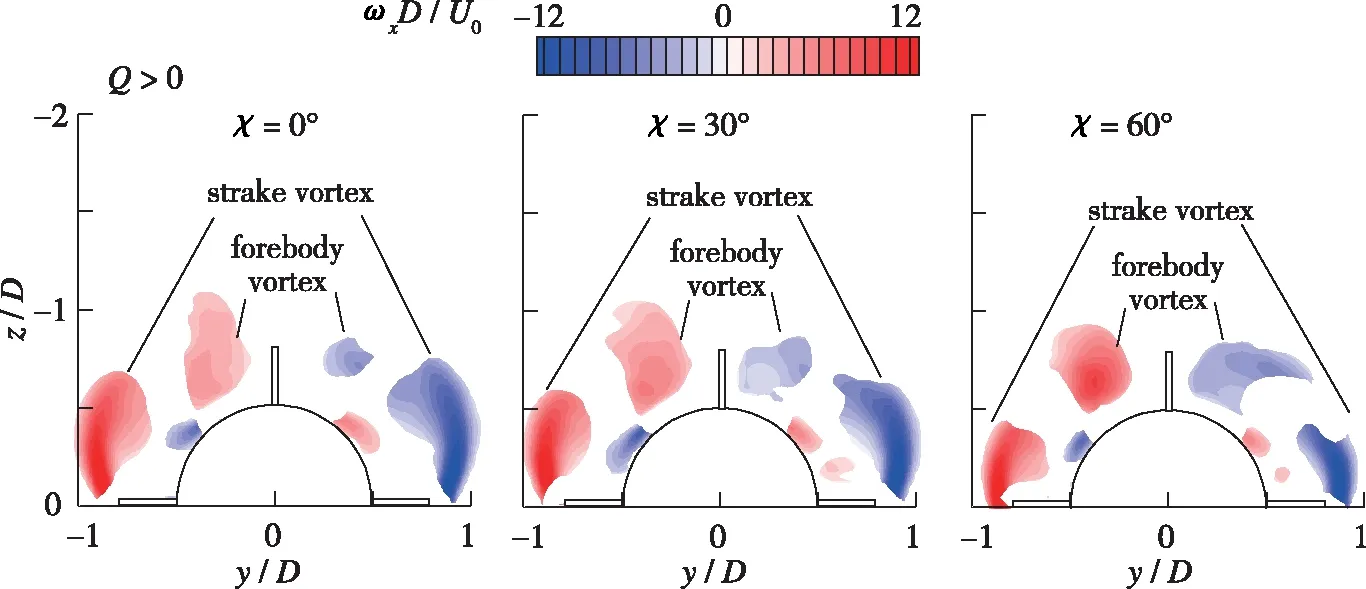
图10 x/D=-2.2截面时均涡量分布

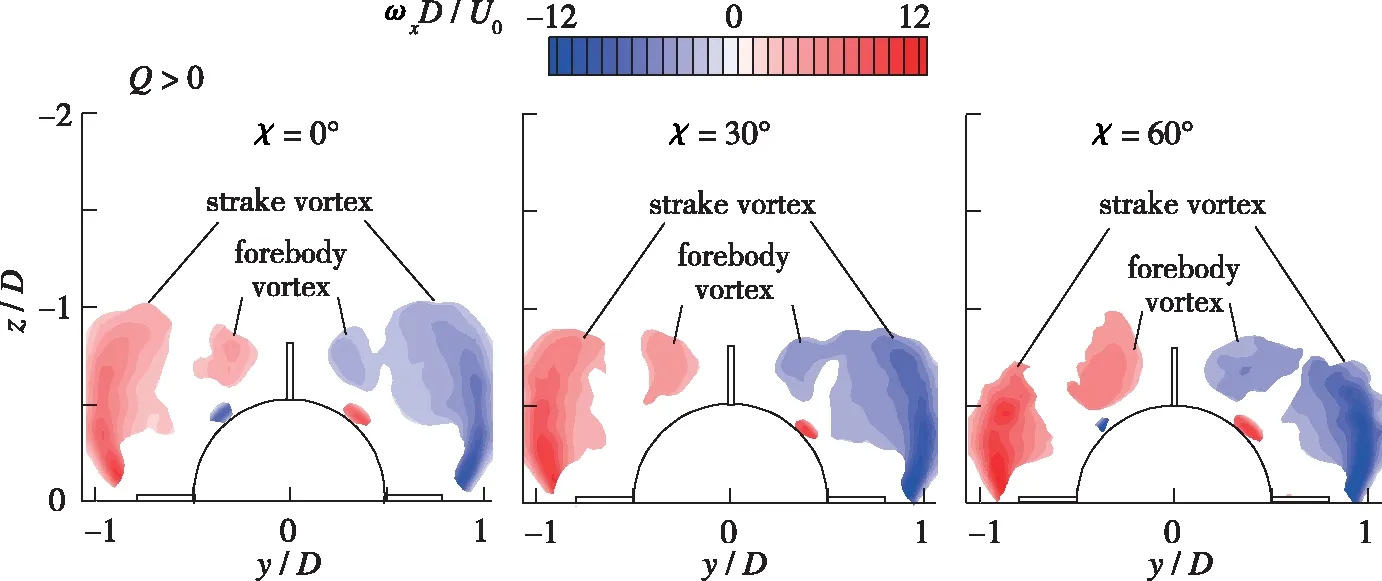
图11 x/D=-2.6截面时均涡量分布

(a)Time-averaged pressure coefficient

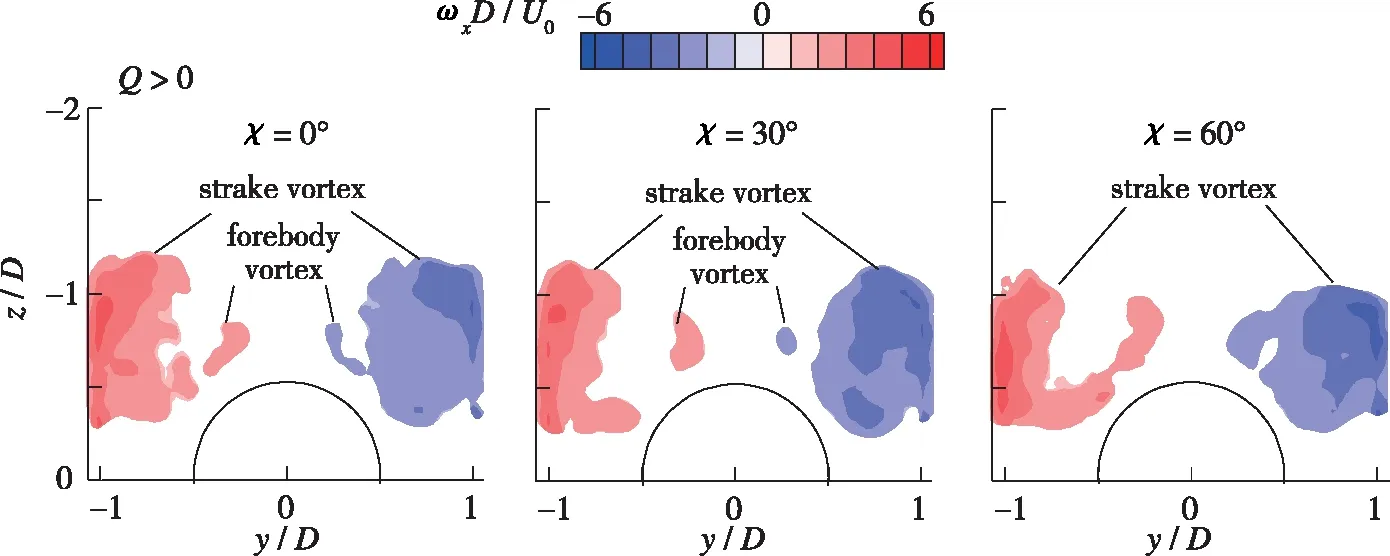
图13 x/D=-3.0截面时均涡量分布

3种边条翼后掠角条件下, 流动均在θ=105°，255°发生分离, 并在θ=135°，225°附近产生吸力峰, 低涡侧的吸力峰更强，因此产生的负压绝对值更大, 对截面侧向力起主要贡献的是θ=135°，225°附近的吸力峰.该吸力峰是由前体非对称涡与边条涡产生耦合流动.随着边条翼后掠角增加, 耦合流动的非对称性增强, 导致截面侧向力系数增大(见图 5), 这与边条翼开始之前x/D=-1.4截面的侧向力随后掠角变化规律相反.

3 结论

本文在亚临界Reynolds数条件下, 对带有边条翼的钝头细长旋成体模型进行风洞实验研究, 分析了边条翼的前缘后掠角对钝头细长旋成体大迎角非对称流动的影响.得到了以下结论:

(1)随着边条翼前缘后掠角的增大, 不仅边条涡与旋成体机身之间距离减小, 而且边条涡的涡轴线基本平行于边条翼后掠前缘, 与钝头细长旋成体的机体纵轴夹角减小, 因此不同后掠角的边条涡对于不同流向位置处的钝头细长旋成体前体非对称涡系的诱导和耦合作用也不同.

(2)在边条翼上游区, 大后掠角边条涡涡位更靠近钝头细长旋成体物面且对称性更好, 因此对前体非对称涡系的诱导作用更强, 使得前体物面的压力分布更加对称, 截面侧向力减小; 在边条翼区, 大后掠角边条翼对前体非对称涡系的诱导作用也更强, 使得旋成体物面的压力分布更加对称且吸力更大; 在边条翼下游区, 大后掠角边条涡涡位远离钝头细长旋成体物面, 因此对旋成体非对称涡系的诱导作用减弱, 使得旋成体物面的压力分布不对称性加剧, 截面侧向力变大.

致谢本文受到国家自然科学基金(11972060, 12002022)、国家自然基金创新群体(11721202)、宁波市自然科学基金(202003N4177)、非定常空气动力学与流动控制工业和信息化部重点实验室开放课题(KLUAFC-E-201902)资助.