Ar介质感应耦合等离子加热器能量转化与流动特性

朱兴营, 陈海群, 曾 徽, 董永晖, 周 法, 刘金涛

(中国航天空气动力技术研究院电弧等离子体应用装备北京市重点实验室, 北京 100074)

引 言

高频感应耦合等离子体(induc ively coupled plasma, ICP)是通过强烈的电磁耦合放电产生的, 不存在电极与等离子体相互接触作用, 因此气氛纯净可控, 同时其仍具有热等离子体高温(～104K)的特点, 且弧区较大, 温度分布比较平坦, 属于“软”的等离子体.基于以上优点, 已有不少利用高频感应耦合等离子加热器设计的高温高焓风洞, 在地面上模拟航天飞行器几近真实的飞行热环境, 进行飞行器热防护材料烧蚀考核试验、防热结构考核试验、材料表面催化特性研究等方面研究工作的报道[1-3], 同时, 高频等离子加热器在材料制备与处理等工业领域同样具有很好的研究和应用价值[4-7].

产生高频等离子体的加热器从结构形式上分为圆柱形和平面形两种, 文中提到的航天及材料工业领域中研究和应用较多的主要是圆柱形结构, 又称H型放电结构, 其工作原理为: 施加在感应线圈上的高频交变电流在等离子加热器内形成磁场, 磁场又进一步感应出环形电场, 环形电场诱导出环形电流, 通过电流的Ohm加热使介质气体被加热和电离形成等离子体[8].从功率上讲, 受高频功率电源现状限制, 目前高频感应耦合等离子加热的功率从数十千瓦到兆瓦量级[9].同时, 通过现有研究可以发现, 目前高频感应耦合等离子加热器的设计主要是基于多年发展起来的感应加热理论、经验公式和试验探索实现的[10], 对加热器内的能量转化与传递特征、流动过程等全局性特征并未过多考虑, 当然, 这很有可能与感应耦合等离子体具有很高的温度且存在强烈的电磁场, 采用传统实验方法难以对加热器内能量分布、温度场、流场等进行全方位的测量和诊断分析是有很大关系的.相比之下, 随着计算技术的发展, 数值模拟趋于快速、准确, 成为可行有效的研究手段之一.通过数值模拟得到高频感应耦合等离子加热器能量和流场分布等特征, 对分析和了解加热器内能量转化过程、热量传递过程和气体流动过程能够起到直观的帮助作用.同时, 随着高频功率电源技术的发展及应用需求的提高, 发展功率更大、工作气体更广泛、应用适用性更强的高频等离子加热器必将成为其未来的发展方向, 对加热器能量转化与流动特性的研究和系统认识也必将对大功率高频等离子加热器结构的设计、气动布局设计、加热器稳定运行等起到积极的作用.

感应耦合等离子体的数值计算研究已经过了几十年的发展, 最早于20世纪60年代, Freeman等[11]，Eckert[12]建立了求解简单的一维热传导方程和一维电磁场方程的一维模型, 之后Boulos发展了求解二维连续、动量与能量方程耦合一维电磁场方程的准二维非自洽模型[13], 之后Mostaghimi等[14-15]和Chen[16]在前面研究的基础上建立了完全二维自洽模型, 该模型综合考虑了磁场的轴向分量和径向分量, 得到满足Maxwell方程的完全自洽电磁场方程, 相较于其他模型, 能够在感应热等离子体的流场结构、温度分布、电磁场特性、线圈结构和工作频率等参数对等离子体特性的影响等方面进行更为准确的计算, 近来年已得到了广泛的应用.本文以完全二维自洽模型为基础, 以中国航天空气动力技术研究院等离子实验室自主研发的百千瓦级柱状感应耦合等离子加热器为对象, 应用COMSOL Multiphysics软件对其进行数值模拟研究, 得到感应耦合等离子加热器内的流场、温度场、能量分布等, 并对能量转化和传递过程、气体流动过程进行分析, 为加热器的发展设计和实际应用提供理论指导和参考.在进行数值模拟计算时, 等离子加热器工作介质为Ar, 计算域扩展到等离子加热器外部有限大小的空气域以模拟外部无限空间的电磁场发展, 此外, 对部分模拟结果与可行实验测量结果进行了对比, 一定程度上验证了数值计算模型建立的合理性.

1 数值模型

1.1 几何模型及网格

本文针对实验室自研的百千瓦级柱状感应耦合等离子加热器建立的几何模型及网格划分如图1所示, 加热器在几何结构上简化为二维轴对称结构, 感应线圈由5匝平行载流圆环构成, 忽略线圈的轴向部分.等离子加热器由中心向外依次包括载气、内环气和外环气3层介质气体, 对应几何结构上包括中心石英管、内环石英管和外环石英管, 等离子加热器外部取与外环石英管长度相同的空气域纳入计算域, 几何模型结构特征尺寸如表1所示.

图1 感应耦合等离子加热器几何结构及网格划分

表1 模型结构特征尺寸

为提高计算的准确性, 对几何模型进行网格划分时, 对感应线圈边界和等离子区域边界划分边界层网格, 对等离子加热器入口处网格进行加密处理, 整个几何模型包含13 347个网格单元.

1.2 控制方程组

通常情况下, 认为感应耦合热等离子体既具有流体属性, 又具有电磁属性, 可采用磁流体力学(magnetohydrodynamic, MHD)方程组对其进行描述, 该方程组包括了质量、动量和能量守恒定律和Maxwell电磁场方程组.同时, 为了在保证计算合理的前提下简化模型, 降低计算量, 做如下假设:

(1)加热器内等离子体为层流、定常流动, 忽略其湍流行为、黏性耗散项和压力做功项;

(2)加热器内等离子体处于局部热力学平衡(local thermodynamic equilibrium, LTE)状态, 此时电子温度、离子温度、原子(或中性离子)温度相等, 可用统一的等离子体温度T来表示.

(3)加热器内等离子体为光学薄, 忽略等离子体对自身辐射能量的吸收, 单位体积等离子体辐射功率是温度的函数.

(4)等离子体为电中性, 忽略Maxwell方程组位移电流项.

基于以上假设, 采用以下二维柱坐标(r-z)系条件下的MHD方程组，对感应耦合等离子体进行描述:

(1)连续性方程

(2)动量守恒方程

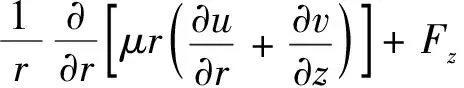
(3)能量守恒方程

(4)电磁场方程

式中,u和v分别为轴向(z)和径向(r)速度分量;ρ,μ,λ,Cp和T分别为等离子体密度、黏性系数、导热系数、比热容和温度;Fz和Fr分别为轴向和径向Lorentz力分量;QJ和QR分别为Joule热和辐射热损耗项;μ0为自由空间磁导率;E和B分别为电场强度和磁感应强度;Jc和Ji分别为线圈电流密度和感应电流密度;t为作用时间.

(1)

(2)

式中,σ为等离子体电导率, i为复数单位,ω为线圈电流角频率,ω=2πf,f为线圈电流驱动频率,a,b分别为Aθ实部和虚部分量.

通过方程式(1)和(2)计算出磁矢势Aθ, 继而计算得到磁感应强度B和电场强度E, 耦合项轴向Lorentz力Fz, 径向Lorentz力Fr和Joule热QJ则分别通过下式计算得到

在利用COMSOL进行数值模拟时, 软件中添加磁场、流体传热和层流3个物理场, 通过对各物理场控制方程进行耦合求解, 得到感应耦合等离子加热器内磁场分布、速度分布、温度分布等特性.

1.3 边界条件

计算时, 中心轴线上电场、温度场及流场边界条件均采用轴对称边界, 即∂u/∂r=∂T/∂r=0,A=0; 入口采用速度入口条件, 载气速度v1、内环气速度v2和外环气速度v3分别为5.5，0.3和3 m/s; 出口采用压力出口条件, 出口压力p为70 kPa; 壁面采用无滑移边界条件, 壁面温度T为350 K; 线圈能量采用功率激励方式, 功率Pw为80 kW(面板功率), 驱动频率f为3 MHz.

2 结果与讨论

2.1 温度分布

图2显示的是高频感应耦合等离子加热器内的温度分布, 从图中可以看出, 等离子体最高温度可达1.06×104K, 最高温度区域轴向上分布在感应线圈所对应的区域, 径向上并不在等离子加热器中心而是对称分布在两侧距外石英管一定距离处, 离开感应线圈所覆盖的区域后, 随着气流的不断下行, 加热器内气体温度整体呈现中心高, 沿径向从中心向两侧温度逐渐降低的趋势, 且在中心较大范围内温度是趋于一致的, 这正是文中提到的高频等离子体弧区较大, 温度分布比较平坦的特点.图3(a),(b)分别显示的是感应耦合等离子加热器内的Joule热分布和电导率分布, 从图中可以看出, 在线圈所覆盖的加热器区域内, Joule热和电导率的分布规律与温度分布是一致的, 即最高值区域分布在线圈覆盖区的外石英管壁附近, 图2, 3结果可综合利用感应放电的趋肤效应进行解释: 等离子体暴露于高频辐射中时, 高频能量与等离子体的相互作用主要发生在表面相互作用层, 称为趋肤深度, 在这里, 高频能量被大量吸收、反射或散射, 因此气体的电离和电热转化也主要发生在趋肤深度区, 电导率高, 感应电流密度大, 产生的Joule热和温度高.加热器中心区气体则主要是通过与趋肤深度区高温气体的热交换进行加热, 因此温度比趋肤深度区低.随着气流下行离开感应线圈所覆盖的区域后, 气流混合逐渐充分, 气流温度趋于一致.

图2 感应耦合等离子加热器内温度分布

(a)Joule heat

图4给出的是感应耦合等离子加热器内z坐标分别为-250，-200，-150和-100 mm的横截面上的温度分布曲线, 其中z=-250 mm截面为加热器出口截面,z=-100 mm截面位于最上匝线圈下沿附近.图中可以看出, 截面上的温度分布如前所述, 呈两侧高中心低的马鞍形状分布, 从截面z=-100 mm 到截面z=-150 mm, 中心温度与两侧的温度差有所增大, 这可能与此段加热器外环冷气由上而下不断被加热有关, 之后随着气流的下行, 中心温度与两侧的温度差不断减少, 在z=-250 mm的截面上, 两者几乎相同, 且呈现由中心向外不断降低的趋势.同时, 对出口截面温度分布曲线进行分析, 当温度降低到最高温度的98%时, 所在截面径向坐标为r=11 mm, 我们可以认为r=11 mm的范围内为加热器出口气流的均匀高温区, 这一区域对于加热器出口气流的利用具有较为重要的意义.

图4 感应耦合等离子加热器内不同横截面上的温度分布曲线

图5给出的是感应耦合等离子加热器上数第2匝与第3匝线圈中间点所在径线(z=-143.5 mm)上的温度分布, 图中实验值是在LTE假设条件下采用发射光谱法测量得到的.从图中可以看出, 数值模拟得到的最高温度区比光谱测量得到的值略高, 两者最大相差240 K左右, 而中心区域温度模拟值则比实验值偏低, 两者最大相差350 K左右.与此同时, 从整体分布上看, 数值模拟得到的温度分布与光谱测量得到的温度分布规律具有良好的一致性, 即最高温度区位于距外石英管一定距离处, 中心温度略低, 相较于实验值, 数值模拟最高温度区更接近于管壁, 两者相差约3.4 mm, 这可能与实验过程中外环石英管外部送入了少量的防止线圈匝间打弧的冷却风, 使得外石英壁面存在一定程度的能量耗散有关.综合以上数值模拟结果与实验结果的比对来看, 采用数值模拟得到的感应耦合等离子加热器内的整体温度分布是比较合理的.

图5 感应耦合等离子加热器内径线上温度分布(z=-143.5 mm)

2.2 速度分布

图6是感应耦合等离子加热器内的速度分布, 从图中可以看出, 最大气流速度为 38.1 m/s, 气流高速度区域分布在最底匝感应线圈及下游的加热器中心区域, 分析原因为介质气体进入感应耦合等离子加热器后, 经过线圈覆盖区域时, 受Ohm加热及对流、传导加热影响, 气体受热温度升高并产生膨胀, 气体速度提高.与此同时, 从图中可以发现, 在等离子加热器内上游几匝线圈所覆盖的区域存在明显的回流区, 该回流区可能是由加热器内感应线圈区域的气流受热膨胀产生的负压力梯度、带电粒子在磁场环境内受到的Lorentz力和Joule加热现象共同作用下产生的[17].

图6 感应耦合等离子加热器内速度分布

图7给出的是气流轴向速度(vz)在感应耦合等离子加热器中心轴线上的分布,vz为负值表示气流向下, 从图中可以看出, 在等离子体加热器中轴线上的气流, 自中心石英管下缘(z=-73.5 mm)开始由上而下, 气流向下流动但速度不断降低, 一段区域内vz变为正值, 即气流向上流动, 之后气流再次向下流动且速度不断增加, 因此, 可以将分布曲线上vz=0的两个点分别作为回流区在等离子加热器中轴线上的上下边缘位置.图中显示, 回流区在中轴线上的上下边缘位置z坐标分别为-85 mm和-125 mm, 即回流区最下缘距离第3匝线圈上端约3.5 mm.

图7 感应耦合等离子加热器内轴心线上轴向速度(vz)分布

针对感应耦合等离子加热器内存在回流区这一问题, 若利用其进行防护材料烧蚀考核等方面的研究时, 加热器下游气流已经过充分发展, 其影响可以不予考虑, 但若利用其进行球形粉末制备等方面的研究和应用时, 则需要穿过回流区再进行送粉而不是在回流区上游或回流区内送粉, 否则送入的粉体容易被气流携带进行反向运动, 继而黏附在石英管内壁上, 倘若粉体是金属材料时, 黏附在内壁上的粉末会形成电磁屏蔽层, 影响等离子加热器的正常运行, 这一点与笔者利用本等离子加热器进行试验研究时出现的现象是高度一致的.

3 结论

本文利用COMSOL对Ar介质条件下百千瓦级柱状感应耦合等离子加热器进行了多物理场耦合的数值模拟研究, 得到等离子加热器内的流场、温度场、能量分布等, 并对能量转化与热量传递、气体流动过程进行了分析, 同时对部分模拟结果与可行实验测量结果进行了对比分析, 得到以下结论:

(1)模拟结果显示, 由于趋肤效应, 感应耦合等离子加热器内最高温度区域对称分布在感应线圈覆盖区距外石英管一定距离处, 加热器中心区域温度略低, 等离子体最高温度可达1.06×104K.随着气流的下行, 气体温度整体呈现中心一定区域内高温且均匀, 向两侧温度逐渐降低的趋势.

(2)发射光谱法测量得到的温度分布与数值模拟得到的温度分布规律具有良好的一致性, 数值模型建立的合理性得到一定验证, 从整体来看, 采用数值模拟手段得到感应耦合等离子加热器内的整体温度分布是比较合理的.

(3)最底匝线圈及其下游的等离子加热器中心区域为气流高速区, 最大气流速度为38.1 m/s, 等离子加热器上游存在回流区, 回流区最下缘距第3匝线圈上端约3.5 mm.