并行建表化学加速算法研究及其在气相斜爆轰模拟中的应用
吴锦涛, 吕一品, 董 刚, 王 帅, 唐 科
(1.北京宇航系统工程研究所, 北京 100076; 2.北京电子工程总体研究所, 北京 100854; 3.南京理工大学瞬态物理重点实验室, 江苏南京 210094)
引 言
高超声速的可燃气流在障碍物作用下可形成驻定于障碍物的爆轰, 即斜爆轰(oblique detona-tion wave, ODW).斜爆轰的本质是激波和对流预混火焰组合成的复合波, 这种由激波主导的燃烧, 具有很高的燃烧效率和传播速度(达几千米每秒).作为一种新型的能量转换模式, 研究斜爆轰为发展高效的热力推进(如斜爆轰发动机,(oblique detona-tion wave engine, ODWE))提供了技术支持[1-3], 因此开展相关研究工作具有重要的科学价值和应用前景.
为精确捕捉斜爆轰波的流场特性, 数值模拟时通常采用详细的化学反应机理对反应源项进行计算, 因此, 对源项的计算过程转化为求解多个由反应速率方程组成的强非线性常微分方程组.由于不同组分的生成/消耗的速率(反应时间尺度)相差很大(实际燃烧和爆轰问题中尺度相差可达9个数量级[4]), 对该方程组的直接积分(direct integration, DI)求解呈现出强烈的刚性现象, 并花费大量的计算用时, 因而需要寻找减少化学反应计算时间的方法.在此基础上, 通过合理的约束条件对详细化学反应机理进行简化的方法应运而生[5-6], 然而, 简化机理的约束条件并不适用于燃烧和爆轰问题中所有可能的化学热力学状态, 可移植性较差.此外, 流场中的部分痕量物质(如某些代表化学反应活性的自由基)的特征时间尺度通常较小, 采用简化机理方法时, 这些组分会被认为满足约束条件而删减, 导致求解过程的失真.
基于此, 通过改进计算方法以在采用详细机理的同时提升化学反应过程的计算效率, 成为避免直接积分求解刚性方程组的又一途径, 动态自适应建表(in situ adaptive tabulation, ISAT)方法[7]就是其中之一.与简化化学反应机理的方法不同, ISAT方法通过在计算机内存中建立化学反应数据表的方式, 将流场内出现的化学动/热力学状态以数据节点的形式进行插入、问询和取回等操作, 取代原直接积分求解.由于对数据节点的存/取操作耗时远远小于求解刚性方程组的耗时, ISAT方法可以很大程度地减少化学反应过程的计算时间.同时, 由于动态建表技术对内存的占用需求不大, 该方法具有很好的可移植性.在低Mach数条件下的定常燃烧数值模拟中, 考虑到流场中一个时间步长内化学反应热力学状态的变化较小, 数据表内的绝大多数节点可以被成功问询并取回利用, 因此, 在这类问题中ISAT方法的计算效率很高.在均质压燃(homogeneous charge compression ignition, HCCI)发动机的计算中, ISAT方法的化学反应加速比可达100倍; 而在配对搅拌发生器(pairwise mixing stirred reactor, PMSR)的计算中, 采用ISAT方法计算化学反应的时间仅为DI的1/42.
然而, 原始的ISAT方法主要局限于低Mach数下的稳态燃烧问题和均相问题的计算中, 其在高Mach数条件下可压缩流的非定常燃烧/爆轰问题中的性能表现仍有待检验.事实上, 可压缩流场中一个时间步长前后化学热力学状态的变化较大, 数据表内的大量节点无法被成功问询和取回, 导致ISAT方法的计算效率下降.同时, 数据表内不断插入的冗余节点(未被取回利用)势必导致表容量的过度增长, 进而突破计算机内存上限, 造成计算过程的中断.为了避免这种情况, Dong等在ISAT方法的基础上作了进一步改进, 即, 添加了整体删除和节点删除两种删除机制, 并基于此提出一种动态存储/删除建立热力学数据表算法[8-9].在激波引发CH4/O2预混气体爆轰问题的二维数值计算中, 动态存储/删除算法计算化学反应源项的加速比达17.88, 总加速比达4.75.
通过上述研究发现, ISAT方法在使用详细化学反应机理的数值模拟中, 具有较好的可移植性, 但其计算效率因物理问题而异.随着近年来大型计算设备的发展, 大规模并行计算日益盛行, 而以ISAT为代表的建表方法也不断被应用于并行数值模拟中.不同于串行执行方式, 在并行执行方式(以MPI并行通讯协议为例)的基础上, 数值计算的每个分区都相当于一个独立的计算区域, 如何在并行环境中生成和构建数据表、并完成各数据表之间的协同合作, 是建表技术在并行计算中应用的一个关键.Lu等[10]首先开展了基于ISAT建表技术的并行计算策略的研究, 在其提出的所有策略中, 最直观的策略是在每个MPI分区内各自独立地生成数据表, 计算过程中, 每个分区的化学热力学状态均在各自对应的数据表内进行插入、问询和取回, 彼此之间没有数据传递.这种并行策略被称之为纯粹本地建表(purely local processing, PLP).此外, Lu等还提出了快速问询(quick try, QT)、均匀随机分布(uniform random distribution, URAN)和优先分配(preferential distribution, PREF)等策略, 并将其应用在CH4/O2预混气体多重混合搅拌发生器的计算中.然而, 针对不同的计算工况, 尤其是流场内热力学状态分布不均匀且随时空变化较大的计算工况, 这些并行策略在计算效率上的表现并不令人满意.这进一步说明, 在并行计算中采用基于建表的化学加速方法, 其计算效率同样取决于具体研究的物理问题, 针对二维斜爆轰这类流场内热力学状态分布严重不均匀且随时空剧烈变化的反应流计算, Lu等[10]提出的策略显然有待进一步的检验.
不同于稳态燃烧问题, 并行计算中爆轰波流场的各个分区的计算负担往往差异很大(如由波阵面组成的间断区和由波后燃烧产物组成的光滑区), 因而在提出并行策略时, 应考虑如何建立与并行分区相应的数据表, 以保证计算过程中不同数据表操作之间的负载平衡性.此外, 由于爆轰问题的特殊性, 计算时数据表中不断有新节点插入, 如何将数据表删除机制[8-9]与并行策略相结合, 以在提升计算效率的同时避免因某个数据表容量突破内存上限导致计算中断.
本文针对二维2H2+O2斜爆轰数值模拟, 提出了几种不同类型的并行策略, 并将这些并行策略与带节点删除机制的动态存储/删除建立热力学数据表方法相结合, 从而形成了适用于瞬态可压缩反应流问题的并行建表化学加速算法, 并从计算精度和计算效率两方面分析了并行策略选取对算法性能的影响.
1 计算方法
1.1 基于ISAT的动态存储/删除建表
考虑带K种不同组分的可压缩反应流流场, 其化学热力学状态向量表达如下
Φ=(Y1,…,Yk,…,YK,T,ρ)
=(φ1, …,φk, …,φK,φK+1,φK+2)
(1)
式中,Yk(k=1, …,K)是组分k的质量分数,T和ρ分别是反应体系的温度和密度.在燃烧过程中, 流场内某单元的Φ0在固定步长Δt内因化学反应带来的状态变化为R(Φ), 具体表达形式为
(2)
式中,Φ0和Φ1分别代表更新前后的热力学状态,S为化学反应源项.式(2)给出了状态方程的DI求解过程.在爆轰等可压缩反应流的计算过程中, 由于不同组分生成/消耗的速率相差很大, 其参与反应进程的时间尺度分布范围在10-9~1 s之间, 这使得S具有强刚性.在对化学反应过程进行DI求解时, 耗时巨大.
不同于直接积分求解, 原始的ISAT方法通过对表中数据的问询/取回操作替代ODE的直接积分求解过程, 从而获取化学变化的近似解.考虑流场中一个待问询的化学热力学状态矢量Φq, 如果数据表中存在某一状态Φ(j)的节点与其足够接近, 那么, 在实际ISAT计算过程中,Φq所对应的化学变化R(Φq)可由存储在数据表中的Φ(j)和对应的R(Φ(j))通过Taylor级数展开获得, 形式如下
R(Φq)=
(3)
其中, ΔΦ=Φq-Φ(j).式(3)对∂R(Φ(j))/(∂Φ(j))的计算和存储产生了节点j状态的梯度映射矩阵A, 通过对矩阵A进行容差判据(εtol)的设定进而可以构造一个以Φ(j)为中心的超椭误差域(ellipsoid of accuracy, EOA).如果状态矢量Φq落在Φ(j)所对应的EOA范围内, 则R(Φq)将通过式(3)获得的R(Φ(j))线性近似值, 这一过程称为取回.由于对数据表的问询/取回操作所耗费的时间明显小于直接积分式(2)求解的计算用时, 因此, ISAT能够起到加速化学反应计算的效果.
值得注意的是, 原始ISAT方法采用线性近似的目的在于让数据表内节点所存储的热力学状态尽可能接近直接积分的结果, 然而, 当流场内化学反应过程十分剧烈(如二维斜爆轰流场)时, 设定EOA判据会导致表中节点难以在后续计算时被成功问询并取回, 进而影响其计算效率.Veljkovic[11]对比了线性近似和常数近似的计算结果发现, 采用零阶精度的常数近似方法, 可以在保证计算精度的基础上改善建表算法在瞬态问题中的计算效率.因此, 本文所采用的动态存储/删除建立热力学数据表算法使用了常数近似取代原ISAT方法中的线性近似, 表达如下
R(Φq)=R(Φ(j))+O(|ΔΦ|)
(4)
在此基础上, 本文重新定义了关于节点Φ(j)的误差范围, 如下

(5)
式中,e+(Φ(j))和e-(Φ(j))分别代指热力学状态Φ(j)的误差上限和误差下限, 等式右边为状态空间内各分量的误差上下限.上述定义实际上构造了一个超矩形误差域(hyper-rectangle of accuracy, ROA), 并且避免了式(3)中梯度映射矩阵A的计算和存储, 计算效率因此得到进一步的提升.此外, 在包含间断的瞬态可压缩反应流问题中, 随着时间的进行, 流场内的热力学状态变化巨大, 表中的大量数据无法被成功取回, 这势必导致数据表内节点数量的急剧上升, 甚至可能会达到计算机内存的使用上限并导致计算中断.针对这一问题, Dong等[8-9]在改进后的ISAT算法中引进了节点删除机制, 有效地控制了数据表的生长.基于以上对ISAT方法的改进, 本文动态存储/删除建表算法的执行流程可以描述如下:
(1)计算开始之前, 首先在计算机内存中建立一个空的数据表.表中第1个节点j的热力学状态矢量由式(2)直接积分而来, 随后, 节点j将记录并保存该状态矢量Φ(j)及其对应的化学变化R(Φ(j))和初始误差数组上下限e±(Φ(j)).
(2)计算开始后, 对流场中每一个待问询的状态矢量Φq, 都首先在数据表中进行查找和比较, 如果表中存在某个节点Φ(j), 使得Φq中的所有分量都能同时满足

(k=1,…,K,K+1,K+2)
(6)
则执行式(4)中的常数近似操作, 将数据表中存储的R(Φ(j))取回, 作为Φq化学反应更新后的变化量, 即R(Φq).这种情况被称为取回成功.
(3)如果式(6)中的条件不能得到满足, 需要通过式(2)中的直接积分求解获取Φq的新的化学变化量R(Φq).同时, 记录并选取在Φq查找路径上的与之最接近的状态矢量Φ(n), 将积分求得的R(Φq)和最接近节点中存储的R(Φ(n))所包含的所有状态分量进行比较, 形式如下
(7)

对节点数据中的ROA误差域执行放大操作是动态存储/删除建表算法中的关键步骤.虽然在当前时间步内, 式(7)中的放大操作无法保证待问询的状态矢量Φq从表中成功取回, 但它能够提高之后的时间步中状态矢量Φ(n)在问询过程中被成功取回的概率.假设下一步计算中某个待问询的状态矢量为Φq′, 如果它能够与在上一步中经过放大ROA范围得到的状态矢量(更新后的Φ(n))满足式(6)中的条件, 这意味着
Φq′=Φ(n)+R(Φq)
(8)
另一方面, 对节点n而言, 经过化学反应更新后的状态矢量Φn′又满足
Φn′=Φ(n)+R(Φ(n))
(9)
因此, 结合式(8),(9)可以发现, 组成Φq′和Φn′的所有状态分量共同构成放大后的ROA误差域的边界, 即
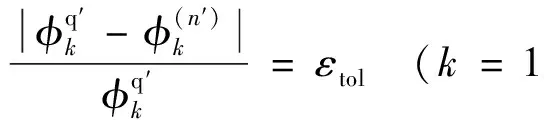
(10)
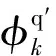
式(5)中的误差数组上下限可以进一步表示成
(11)
其中, 相对误差和绝对误差的初始值在本文中分别给定为εr=1×10-3和εa=1×10-8.当问询矢量满足式(5)的条件时, 节点数据在ROA误差域内的取回精度由εr的值决定.否则, ROA误差范围将被一定程度地放大, 因而在随后的计算中, 经过放大操作的ROA误差域所对应的新的取回精度将由式(10)中εtol而非εr决定.换句话说, 数据表中节点的初始εr越小, 计算过程中可能发生的放大操作越多, 因而该节点实际的取回精度最终将取决于εtol的设定; 相反, 数据表中节点的初始εr越大, 对ROA的放大操作发生的次数就越少, 因而该节点内部所存储的热力学状态将主要取决于初始εr的设定.
实际计算过程中, 通常会设定相同的εr和εtol, 以保证节点参数的取回精度不受放大操作的影响.不同的是,εr的值在节点插入数据表的时刻已经给定, 因而只能局部地影响该节点的数据取回精度; 而εtol可以在整个计算过程中动态地控制数据节点的ROA误差范围, 因而具有全局的影响.考虑到εtol对动态存储/删除建表算法精度有明显影响, Dong等[8]在激波聚焦引发爆轰波起爆的数值模拟中, 研究了不同容差判据(εtol)下建表加速算法的表现.结果表明, 一味地增大εtol虽然能够明显地提升计算效率, 但势必会导致计算精度的下降.为同时兼顾建表加速算法在计算精度和计算效率上的表现, 本文将容差判据设定为εtol=1×10-3, 该大小的容差判据在瞬态可压缩反应流问题[8-9]中被证明是可靠的.另外, 通过设定绝对误差(εa=1×10-8)保证数据节点中状态矢量各个分量φ(j)的非负性.在实际计算过程中, 对任意分量k, 需要满足φk(j)≥εa/(1-εr)≈1.001×10-8, 因此, 本文设定一个足够小的下限指标1.005×10-8, 当计算过程中φk(j)小于这个值时, 令φk(j)=1.005×10-8, 以保证反应系统中所有化学热力学状态分量在给定误差数组上下限时的物理真实性.需要注意的是,εa的量纲随着状态分量的量纲而发生改变.当φi(j)代表组分浓度时φa是一个无量纲量(φa=1×10-8); 当φk(j)代表温度时,εa等于1×10-8K; 当φk(j)代表密度时,εa等于1×10-8kg/m3.
(4)针对包含复杂流场结构的瞬态可压缩反应流问题(如本文中的气相爆轰波传播), 流场内化学热力学状态随时空的变化十分剧烈, 这会导致数据表中已插入的大量数据节点无法被成功取回利用.因此, 随着计算的进行, 不断有新的节点会插入到数据表中并导致其过度增长.对于有限的计算机内存空间而言, 持续增长的数据表尺寸最终将达到计算机内存的使用上限, 从而导致整个计算过程被迫中断.为了避免这一现象, 本文提出一种数据表尺寸控制策略, 该控制策略由单表尺寸(single table size,Msin)控制方法和总表尺寸(total table size,Mtot)控制方法组成.其中, 单表尺寸控制方法意味着通过单个数据表内节点数量的删除上限来控制表的尺寸, 计算过程中, 当某个数据表中节点数量到达Msin时, 节点删除操作将被激活, 并检查表内已插入的所有数据节点, 将之前的计算过程中未被重复取回利用的节点删除.总表尺寸控制方法则是针对并行计算多数据表专门提出的控制方法, 其通过所有数据表内节点数量总和的删除上限来控制表的尺寸.在计算的每一个时间步内, 首先统计所有数据表中的节点数量总和, 当总和大于Mtot时, 节点删除操作将在全局范围内激活, 并清除所有数据表内未被重复取回的节点.此外, 本文进一步优化了原节点删除机制[12], 当数据表内节点数量到达上限(Msin或Mtot)后, 整个之前的计算过程(而非上一时间步)中被重复利用过的节点数据, 都将被保留.优化后的节点删除机制虽然会导致数据表内节点的累积, 但却能够进一步减少重复的直接积分运算.
1.2 并行策略
在基于MPI通讯协议的并行化学反应流数值模拟中, 原本完整的计算区域被分成若干个计算分区, 因此, 在数值模拟的过程中往往存在多个数据表, 每个数据表对其中的一个分区进行操作, 故实现并行加速算法的重要手段是需要考虑并行计算中各个数据表的操作及其之间相互作用的方法或策略.其中, 最直观和最易实现的一种并行策略是Lu等[10]提出的纯粹本地建表(purely local process-ing, PLP)策略, 见图1(a).在PLP策略中, 所有ISAT数据表均建立在其本身所对应的计算分区中, 在实际计算过程中, 所有数据表操作只能在对应的(即本地的)分区内执行, 彼此之间没有数据传递.在有些燃烧问题中, 由于流场内不同并行计算分区之间的热力学状态分布相似, 因此, 各分区内的数据表所承担的计算任务相当, 各个数据表的表操作效率基本相同, 从而使得PLP策略能够满足化学加速计算的需求.然而, 在包含间断的瞬态可压缩反应流问题中, 不同分区之间的化学热力学状态分布可能差异很大, 并且随时间会发生剧烈变化, 因此, 传统的PLP策略[10]并不总能保证各分区所对应的数据表在化学反应处理(操作效率)上的均衡, 从而导致计算效率的下降.因此, 本文针对二维爆轰波数值模拟提出了一种全新的并行策略, 转置建表策略(transposed processing, TP), 如图1(b)所示.在该策略中, 数据表(T1-Tn)按序建立在其对应分区(S1-Sn)转置后的位置上.
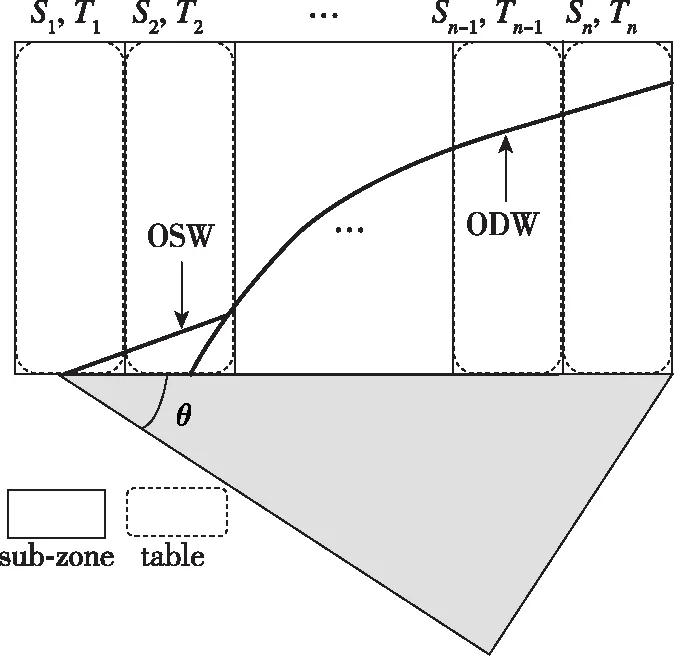
(a)Purely local processing strategy
在二维数值模拟中, 当爆轰波传播方向与分区边界相垂直, TP策略可以均匀划分包含间断的剧烈反应区, 并将它们分配到各数据表中以保持表操作的负载均衡.相应地, 当爆轰波传播方向与分区边界平行时, PLP策略同样具有上述计算优势.因此, PLP策略和TP策略被认为是两个等价策略.针对流场中不同的爆轰波构型, 选取合适的并行策略可以有效地提升数据表操作之间的负载均衡性.因为这两种策略决定了并行计算中各数据表的初始结构, 本文将PLP策略[10]和TP策略合称为底层建表策略.
在实际计算过程中, 二维爆轰波的传播方向并不总与分区边界正交(如本文所研究的二维斜爆轰计算), 这意味着, 针对某种爆轰波构型, 即使选取了适用的底层建表策略, 仍不能总保证每个数据表在操作效率上的一致.另外, 考虑到瞬态问题中化学热力学状态分布的随机性和不稳定性, 在某个具体的时间步内, 各数据表所执行的表操作并不完全一致.当随机性和不稳定性发生在流场内化学反应比较剧烈的区域时, 这种不一致性会愈发明显.在此基础上, 本文提出了另一类并行策略, 即, 负载均衡策略, 以进一步改善数据表操作上的负载均衡性.所提出的负载均衡策略包括数据分摊策略(data apportion processing, DAP)和数据交换策略(data exchange processing, DEP), 两种策略的原理见图2.

(a)Data apportion processing strategy
DAP策略的基本思想可以理解为: 对计算过程中的每个时间步, 通过比较不同数据表的表操作时间, 将操作时间长(操作效率低)的数据表中的一部分计算任务通过MPI协议函数分摊到操作时间短(操作效率高)的数据表中, 让后者帮助前者处理.当针对这部分任务的数据表操作完成之后, 再将其返回到原数据表中, 以尽可能提高不同数据表操作效率之间的一致性.DAP策略的具体执行方式如图2(a)所示.在每个时间步(大于等于第2步)计算开始之前, 首先对所有数据表操作耗费的累计CPU时间(墙上时间)做统计和排序.依次地, 将耗时最长的数据表(记为Tmax)中一半的节点通过分摊操作传递给耗时最短的数据表(Tmin), 将耗时第二长的数据表的一半节点分摊给耗时第二短的数据表, 直到所有数据表都完成配对为止.需要注意的是, 当并行计算中分区/数据表的个数n为偶数时, 配对数量为n/2; 当n为奇数时, 配对数量为(n-1)/2, 而剩余的单个数据表因其计算效率恰好居中, 不对其进行数据分配的操作.以上数据传递过程结束之后, 各个数据表所需处理的计算任务将不完全相同, 从数量上来看, 作为接收方的数据表需要承担的计算任务是作为发送方的数据表任务的3倍; 但是, 从计算时间上来看, 配对数据表双方在该时间步内进行表操作所耗费的CPU时间将比分摊之前更加接近, 这是由各数据表在操作效率上的差异导致的.当此时间步内所有数据表的化学反应计算完成之后, 被分摊的一半节点将返回原数据表, 该时间步内的计算结束.接下来, 在下一个时间步的化学反应计算开始之前, 再对各数据表操作的累计CPU时间重新排序, 然后再进行分摊操作.可以看出, DAP策略的根本目的在于改善数据表操作效率上的负载均衡性, 而其中每个表需要处理的计算任务多少相互之间并不相同.
相应地, DEP策略同样依赖于MPI通讯协议对各数据表的计算任务进行重新分配, 但该策略是在数据交换操作的基础上完成的.DEP策略的具体执行方式如图2(b)所示, 在每一计算时间步开始之前, 数据表根据操作时间进行排序和配对的方式和前面的DAP策略相同, 但不同的是配对后的两个数据表的数据传递将从DAP中的单向传递关系变化为DEP中的双向传递关系.因此, DEP策略能够在提升数据表操作负载均衡性的同时, 保证各个数据表所需处理的任务量一致.需要注意的是, 数据表在化学反应操作中耗费的CPU时间主要依赖于热力学状态的分布而非计算任务的多少, 因此, 单独比较DAP和DEP策略, 并不能直接得出谁更好的结论.通常认为, 当各个数据表需要处理的操作任务(流场内的化学热力学状态分布)差异较小时, DEP策略的计算效率要高于DAP策略, 反之, 则DAP策略的效率更高.
2 二维斜爆轰数值模拟
2.1 控制方程和计算格式
针对二维2H2+O2斜爆轰问题的数值模拟, 本文采用基于理想气体的带二维详细化学反应机理的多组分Euler方程求解, 控制方程表达如下
(12)
其中

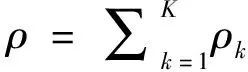
计算时采用分裂算法将控制方程(12)中的对流项和化学反应源项解耦处理, 在规定的每个计算时间步内, 首先在不考虑化学反应的情况下计算流动过程, 然后利用流动过程更新后的流场参数计算化学反应过程.针对反应源项S采用经典2H2+O2详细机理[14], 其中包含9种化学反应组分和19个基元反应, 分别通过并行建表化学加速算法和直接积分方法求解.流动过程(F和G)采用Lax-Friedrichs通量分裂格式结合高精度9阶WENO格式[15]计算.最后, 采用3阶显式Runge-Kutta方法处理时间项U, 计算的定时间步长为1.0×10-9s.
2.2 计算模型
针对二维斜爆轰波流场建立的数值计算模型如图3所示.图中矩形区为计算区域,x方向上的长度(Lx)为15 mm,y方向上的长度(Ly)为 7.5 mm.初始来流为当量比H2∶O2∶N2=2∶1∶4的超声速可燃预混气体, 初始温度和初始压力分别设置为T0=298.15 K和p0=1 atm(1 atm=1.013 25×105Pa).图3中楔形区域(灰色部分)的半锥角θ代表了来流与楔平面之间的角度, 本文计算中设定来流Mach数和半锥角分别为Ma=7.0和θ=30°.计算初始时刻, 斜激波和斜爆轰波在流场中的位置和角度可以根据Ma和θ由斜激波关系式[16]求出.在整个计算区域中, 楔形表面对应的边界采用绝热滑移刚性壁面条件, 其他边界均采用零梯度边界条件.为精确捕捉二维斜爆轰流场内的波系结构, 使用尺寸为Δx=Δy=0.01 mm的均匀正交网格覆盖图3所示的整个计算区域范围.基于该网格尺寸, 流场内半反应区的长度包含了约24个网格, 足以描述斜爆轰波流场的精细结构.

图3 二维斜爆轰流场示意图(OSW—斜激波, ODW—斜爆轰波, CW/DW—燃烧/爆燃波)
计算开始后, 由于可燃预混气流的超声速传播, 首先会在图3所示的楔面上方形成以楔形顶点为起点的OSW, 楔面与斜激波之间的角度由来流的Mach数决定.此后, 来流中的可燃预混气体被斜激波诱导燃烧, 并通过化学反应释放能量支持斜激波传播, 进而在流场(见图3)下游形成ODW.从OSW到ODW的发展过程, 通常伴随着流场内复杂的波系结构变化, 包括DW和CW.此外, 计算初期斜爆轰波阵面在下游所处的位置并不驻定.为了避免上述这些非物理过程的影响, 本文选取稳定阶段的10 000个时间步(8 000~18 000)作为斜爆轰波数值模拟的一个完整的计算过程.图4给出了计算结束时刻(时间步18 000), 采用直接方法计算化学反应得到的斜爆轰波流场密度分布图, 图中清晰地显示了包含斜激波、斜爆轰波、爆燃波以及它们汇聚形成的三波点等波系结构.定义从楔顶点到三波点的水平距离(x方向)为斜爆轰波的诱导区长度, 经统计, 本文数值模拟的诱导区长度为5.0 mm, 这与文献[16]中计算得到的诱导区长度一致, 表明了本文计算模型和数值方法的合理性及可靠性.

图4 直接积分求解的计算结束时刻(时间步18 000)2H2+O2斜爆轰波流场的密度分布图
3 结果与讨论
为考察基于不同并行策略的化学加速算法在二维斜爆轰波数值模拟中的表现, 本文分别采用了基于PLP策略的3种算法与基于TP策略的3种算法, 对化学反应过程进行加速计算, 并与DI求解化学反应过程的结果对比, 考察并行建表化学加速算法在计算精度和计算效率两个方面的表现, 见表1.
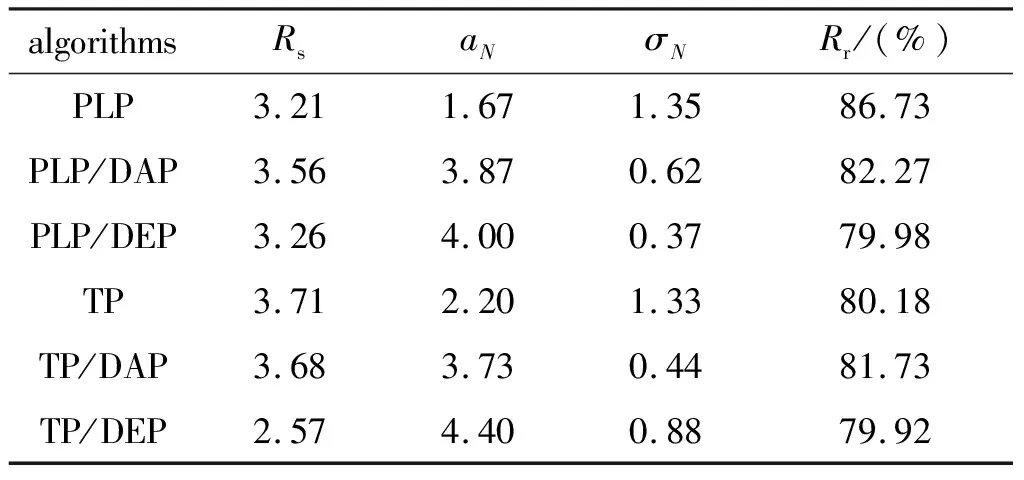
表1 并行建表化学加速算法在二维斜爆轰波数值模拟中的计算性能
本文所有算例(包括直接积分算例)均采用15个MPI并行分区, 每个分区对应一个数据表, 且将数据表的容差判据统一设定为εtol=1×10-3.根据计算机内存空间上限, 将总表尺寸和单表尺寸分别设置为M5=12.0×107和Msin=1.8×107.
3.1 计算精度
在二维斜爆轰波流场中, 由斜激波和斜爆轰波连接组成的波阵面与计算区域的两个方向(x和y方向)存在明显的倾斜角(见图4).在此基础上, PLP策略和TP策略在本文流场中的应用效果存在“先天的”相似性, 故基于两种策略的各算法在计算精度上的表现也比较相似.因此, 本文只考察基于TP策略的3种并行建表化学加速算法(TP,TP/DAP和TP/DEP)的计算精度.图5首先给出了计算结束时刻(时间步18 000)3种算法计算的2H2+O2斜爆轰波二维流场图, 并将其与对应的直接积分结果作对比.结果表明, 基于TP策略的3种算法计算得到的压力、密度和温度的分布结果均与DI的结果高度一致, 反映了本文提出的并行建表化学加速算法在斜爆轰数值模拟中的精确性.
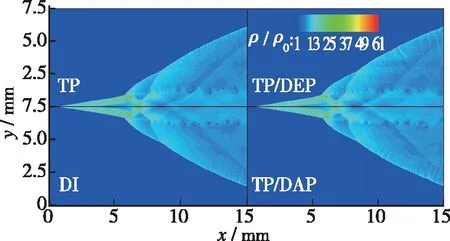
(a)Density
为定量分析带数据表尺寸控制策略的并行建表化学加速算法在二维斜爆轰波数值模拟中的计算精度, 图6给出了结束时刻(时间步18 000), 基于TP策略的3种算法和DI计算的紧靠楔形表面的一层网格内(y=0 mm), 压力、温度以及组分OH和H2O2的质量分数沿x方向的分布曲线.结果表明, 基于TP的3种算法对不同物理量的计算结果均与DI结果保持高度一致, 再次反映了并行建表化学加速算法的精确性.图6中的结果还指出, 各算例(包括DI)对应的积分量分布曲线在流场下游位置均存在一定程度的波动.这是由瞬态反应流问题本身的数值不稳定导致的, 与并行建表化学加速算法的使用无关.综上, 通过与DI计算结果的对比发现, 并行建表化学加速算法在二维斜爆轰数值模拟中的计算精度可靠, 因而可以进一步考察算法在斜爆轰波数值模拟中的计算效率.

(a)Pressure
3.2 计算效率
为考察带数据表尺寸控制策略的并行建表化学加速算法在二维斜爆轰波数值模拟中的计算效率, 图7首先给出了各算法在整个计算过程(时间步8 000~18 000)中的加速比Rs曲线, 加速比定义为采用直接积分求解化学反应过程的时间与采用加速算法求解化学反应过程的时间之比.总体来说, 各算法的加速比曲线都经历了初始阶段的持续增长过程, 且计算初期的增长率更高.对比两种由底层建表策略(PLP和TP)直接构成的算法可以发现, 纯粹TP算法的加速比明显高于纯粹PLP算法, 这表明TP算法通过转置操作带来的数据传递有利于提升不同数据表操作之间的负载均衡性.

图7 2H2+O2斜爆轰波数值模拟中各并行建表化学加速算法在整个计算过程(时间步8 000~18 000)中的加速比曲线
此外, 比较纯粹算法和复合算法在加速比上的差异可以发现, 当选择不同的底层建表策略时, 负载均衡策略(包括DAP和DEP)对计算效率的作用也不同.在基于PLP策略的算法中, 复合算法PLP/DAP和PLP/DEP的加速效果均高于纯粹PLP算法; 而在基于TP策略的算法中, TP/DAP和TP/DEP两种复合算法的加速比反而不如纯粹TP算法.计算结束时刻(稳定阶段), 各算法的化学反应加速比取值见表1, 所有算例中, 纯粹TP算法的计算效率最高(Rs=3.71).
为了分析不同算法在计算效率上的差异, 图8选取了加速比最高和最低的两种算法(纯粹TP算法和TP/DEP算法), 绘制了几个典型数据表(T4,T6,T13和T14)在整个计算过程中的建立/删除成长过程曲线.在选取的4个典型数据表中,T4和T6对应的流场区域内均包含有部分爆轰波阵面; T13对应的区域为流场内的已燃气体; 而T14对应的区域内包含了三波点和反应诱导区.图8的结果表明, 纯粹TP算法中不同数据表执行节点删除操作的次数具有一定的差异; 而TP/DEP算法中4个典型数据表执行节点删除操作的次数几乎相同, 说明叠加DEP策略可以有效改善数据表计算负载上的不均衡.此外, 通过观察图8中不同数据表执行节点删除操作的时间步可以发现, 引入数据表尺寸控制策略, 表操作尤其是节点删除操作发生的时机具有很高的同步性, 避免了计算过程中不同数据表操作之间相互等待的时间耗费.

(a)Single TP algorithm
表1给出了不同算法中所有15个数据表执行节点删除次数的标准差(σN)取值, 用于表征各算法在数据表操作负载均衡性上的差异.结果显示TP/DEP算法的取值要低于纯粹TP算法, 再次验证了DEP策略对负载均衡性的提升.然而, 通过表1中数据表执行节点删除操作的平均次数(表1中aN)可以发现, 纯粹TP算法在整个斜爆轰数值模拟过程中所有15个数据表节点删除操作的平均次数只有2.2次, 明显小于TP/DAP和TP/DEP两种复合算法.节点删除操作的次数代表了计算过程中数据表内插入节点的频次, 通常由数据表内节点的重复取回比例决定, 更小的节点删除操作次数意味着表内更多的节点被取回, 也即直接积分插入节点的数量更少.表1进一步给出了各算法中所有15个数据表内节点取回率(定义为数据节点成功取回次数与数据查询次数的比值)的平均值, 可以发现不同算法在平均取回率上的表现相近, 而纯粹TP算法中数据节点的插入次数明显更少, 意味着其中数据表节点的取回次数更高.综合来看, 纯粹TP算法中各数据表的计算负载比较均衡且同步性较高, 在此基础上, 通过DEP策略只能一定程度地提升计算效率.同时, 由于纯粹TP算法执行节点删除操作的平均次数更少, 意味着需要重新积分插入新节点的次数也相对更少, 在数据节点取回率相近的基础上, 控制节点插入的数量可以有效避免大量直接积分求解刚性方程的时间, 提升化学反应过程的计算效率.
图9进一步给出了纯粹TP算法中, 几个典型数据表(T4,T6,T13和T14)在状态空间中的可达区域和可重复区域, 以表征2H2+O2斜爆轰波数值模拟中流场不同位置对应的数据表内的热力学状态分布.可达区域(图9中灰色散点)可以理解为整个计算过程中斜爆轰波流场内实际出现的所有化学热力学状态的集合; 可重复区域(图9中黑色散点)则可以理解为整个计算过程中流场内重复出现的化学热力学状态的集合.

图9 纯粹TP算法中典型数据表(T4, T6, T13和T14)在化学热力学状态空间中的散点分布图
从可达区域的范围来看, 不同数据表内出现的化学热力学状态范围明显不同, 包含三波点和反应诱导区在内的数据表T14的可达区域范围明显比其他数据表更为复杂.从可重复区域对可达区域的覆盖情况来看, 数据表中能够重复取回利用的热力学状态范围较大, 尤其在数据表T14对应的计算区域内, 大量数据节点可以被重复取回利用(经统计纯粹TP算法中数据表T14的取回率达到91.35%).考虑到该区域内的化学热力学状态十分复杂且变化剧烈, 对应数据表内可重复区域的覆盖率高意味着直接积分操作的次数少, 进而解释了纯粹TP算法更高的化学反应加速比.
结合表1的结果可以发现, 更大的可重复区域范围使得数据表中能够取回重复利用的热力学状态更多, 计算过程中节点删除操作的平均次数更少.在此基础上, 每个数据表内包含的有效节点数量已经基本涵盖了对应分区内的热力学状态, 而通过DAP和DEP进行数据传递后, 表内被引入大量其他计算区域对应的化学热力学状态节点, 导致了数据表内节点插入和删除的次数增加, 影响了化学反应过程的计算效率.因此, 纯粹TP算法在2H2+O2斜爆轰数值模拟中的计算效率更高.
4 结论
本文以带节点删除机制的ISAT方法为基础, 针对可压缩反应流的大规模并行数值模拟手段, 构造了几种基于数据表操作的并行策略, 并由此提出了一系列并行建表化学加速算法, 将其运用到二维2H2+O2斜爆轰数值模拟中, 考察了其在计算精度和计算效率上的表现.研究结果表明, 本文提出的基于不同策略的所有并行建表化学加速算法, 均能在不损失计算精度的基础上有效提升化学反应过程的计算效率.对比不同算法的化学反应加速比发现, 并行策略的选取对计算效率具有明显的影响.在包含15个分区的所有算例中, 基于PLP策略的复合算法(PLP/DAP和PLP/DEP)比纯粹PLP算法的计算效率更高; 而基于TP策略的复合算法(TP/DAP和TP/DEP)则比纯粹TP算法的计算效率更低.在所有算例中, 纯粹TP算法在计算结束时刻的化学反应加速比最高(Rs=3.71).通过分析斜爆轰流场化学热力学状态空间的分布规律发现, 状态空间内可重复区域对可达区域的覆盖率越高, 数据表内节点被重复取回利用的次数就越多, 整个计算过程中数据表执行节点删除操作的次数也就越少, 并最终体现为更高的化学反应加速比.
致谢感谢国家自然科学基金(11702032)和航天一院CALT联合基金(CALT2020-ZD01)对本文的大力支持.

