基于多轴联动控制的内齿珩轮强力珩齿齿向修形工艺研究

王少杰, 夏 链, 韩 江, 刘海军

(合肥工业大学 机械工程学院,安徽 合肥 230009)

由于受到安装误差、制造误差和齿轮变形等因素的影响,齿轮在传动过程中易产生啮入、啮出冲击以及噪声和振动。实际生产中大多数齿轮都需要进行齿向修形,使其在传动时受载均匀、减少啮合冲击。珩齿工艺因其对热处理后的齿轮有很好的误差修正能力而得到广泛采用[1],珩齿修形加工后的齿轮具有良好的齿面精度和传动性能。

文献[2]提出对齿轮进行齿向修形以改善齿轮的接触特性和承载能力;文献[3]研究了3种附加运动进行齿向修形的方法及其对齿形的影响;文献[4]基于五轴数控成形磨齿机,提出将机床各轴运动拟合为高阶多项式对齿轮进行齿向修形;文献[5]提出用B样条曲线对砂轮轴向廓形进行拟合,再基于机床各轴敏感性分析的高阶修正模型对齿轮进行拓扑修形;文献[6]研究了接触线与齿向修形的关系,通过调整砂轮安装角对接触线进行优化，以提高齿向修形的精度;文献[7]针对齿向任意修形齿轮的精密加工问题,提出一种连续展成磨削运动轨迹规划方法;文献[8]提出用与工件齿轮相同齿面的金刚石修整轮修整珩轮的方法来得到目标工件齿轮;文献[9]提出将珩齿机床运动拟合为高阶多项式形式对齿轮进行拓扑修形。

综上所述,许多学者对齿轮修形加工工艺进行了大量研究,但主要集中在磨齿加工上。珩齿修形加工目前仍是采用专用的金刚石修整轮修磨珩轮,将修形参数复映到工件齿轮上,不同的修形参数需要制造不同的金刚石修整轮,这种加工方式成本昂贵、齿轮生产周期长。

本文基于已有的研究,根据珩齿加工运动机理提出通过多轴联动的方式来进行齿向修形,实现不需要调整金刚石修整轮,仅需根据修形曲线调整机床运动即可加工出所需的修形齿轮。

1 内齿珩轮齿面数学模型

内齿珩轮和工件齿轮啮合属于交错轴斜齿轮啮合,加工时珩轮表面磨粒通过滑移和挤压的方式去除工件表面材料。在珩齿加工过程中,首先要用金刚石修整轮对珩轮齿面进行修整,再利用修整后的珩轮对工件齿轮进行展成加工。因此,需要根据金刚石修整轮修整加工机理构建内齿珩轮齿面数学模型。

1.1 金刚石修整轮齿面方程

金刚石修整轮齿面是标准的渐开线螺旋面,如图1所示。

根据渐开线螺旋面的形成原理,在坐标系Sd(Od-xdydzd)中,金刚石修整轮齿面上任意点M的位置矢量和法向量可以表示如下:

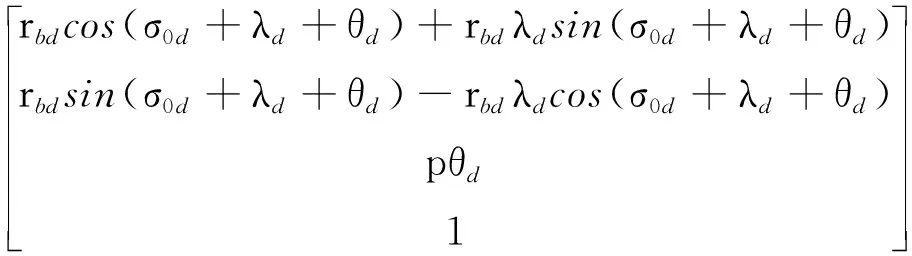
(1)

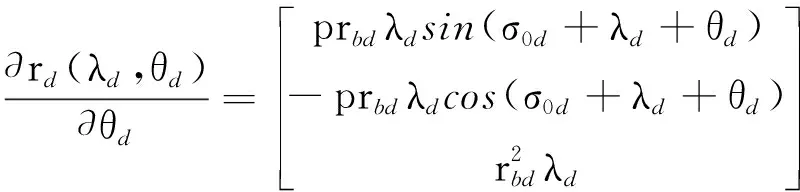
(2)

其中:p=rd/tanβd=rbd/tanβbd为齿面螺旋参数;rbd为修整轮基圆半径;θd为螺旋增量角;λd为渐开线增量角;σ0d为渐开线起始角。

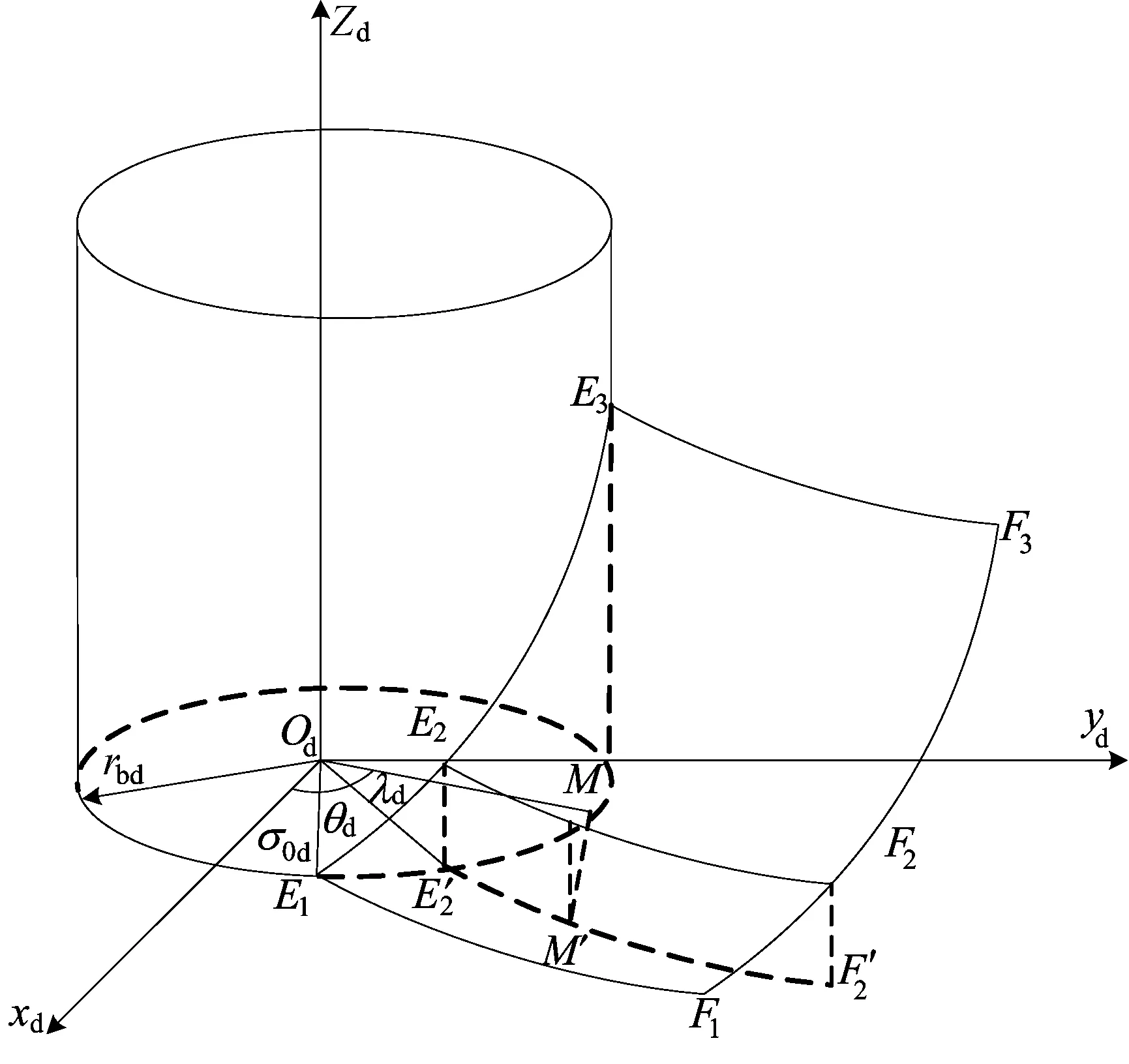
图1 金刚石修整轮齿面坐标系

1.2 金刚石修整轮修整运动模型

内齿珩轮强力珩齿机床(如Y4830CNC型)有7个运动轴,如图2所示。

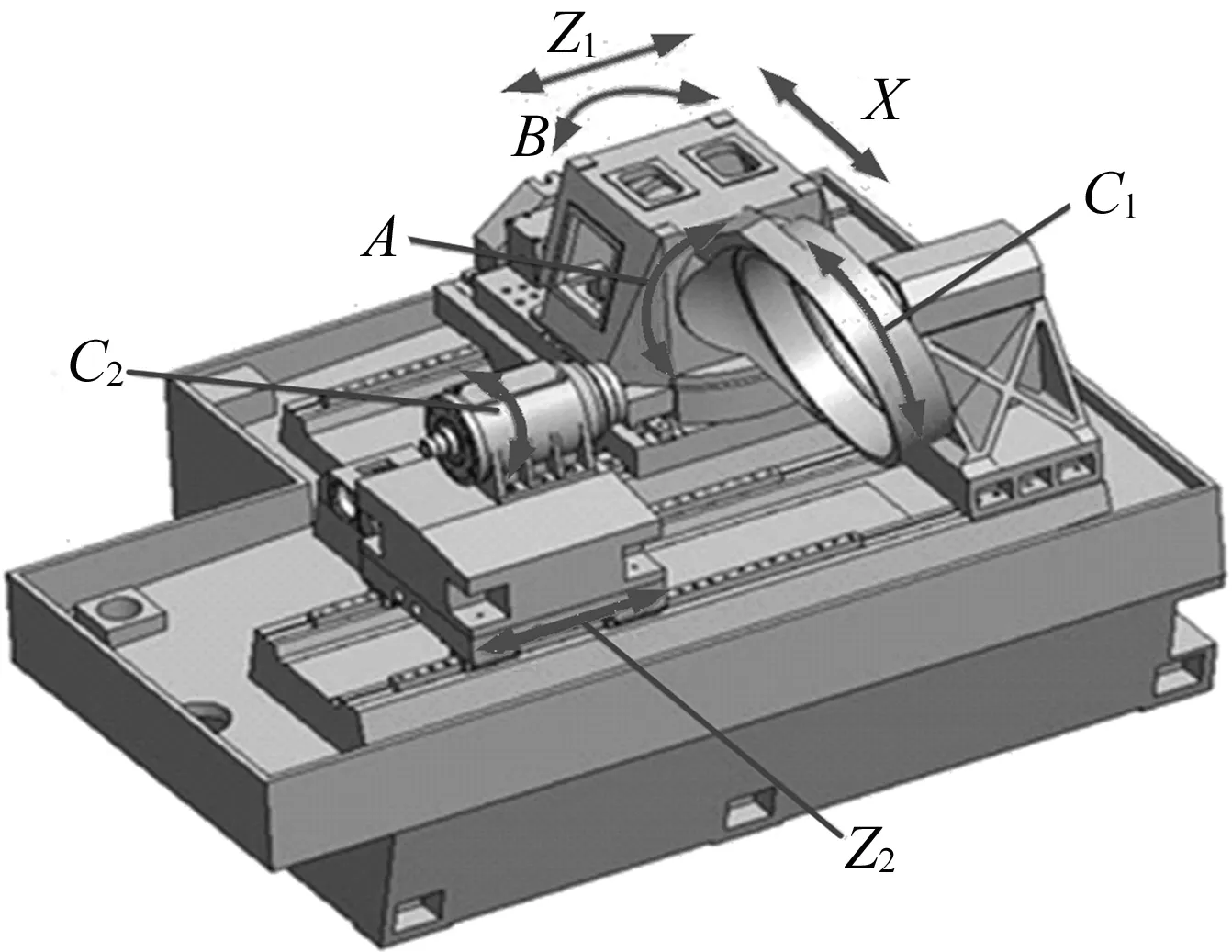
图2 Y4830CNC内齿珩轮强力珩齿机模型

图2中:X轴为珩轮径向进给轴;Z1轴为珩轮轴向进给轴;Z2为工件移动轴;A轴为轴交角调整轴;B轴为珩轮摆动轴;C1轴为珩轮旋转轴;C2为工件旋转轴(金刚石修整轮旋转轴)。

根据机床结构和各轴运动关系建立金刚石修整轮修整加工运动坐标系,如图3所示。其中:坐标系Sd(Od-xdydzd)和Sh(Oh-xhyhzh)为固联于金刚石修整轮和内齿珩轮的运动坐标系;坐标系S1(O1-x1y1z1)和S2(O2-x2y2z2)为方便于坐标变换的辅助坐标系。

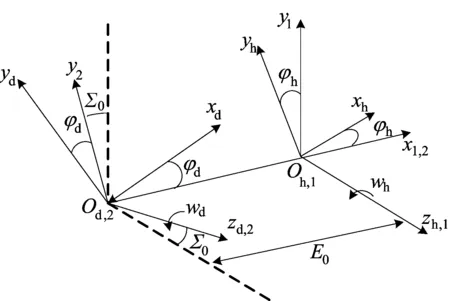
图3 金刚石修整轮修整加工运动坐标系

通过坐标系间的坐标变换,在坐标系Sh(Oh-xhyhzh)中珩轮齿面的位置矢量和法向量可以表示如下:

Mhd(φd)rd(λd,θd)

(3)

Lhd(φd)nd(λd,θd)

(4)

Mhd=Mh1M12M2d,

(5)

(6)

其中:Mhd为坐标系Sh(Oh-xhyhzh)和Sd(Od-xdydzd)的坐标变换矩阵;Lhd为Mhd去除最后一行和最后一列的子矩阵;E0为金刚石修整轮与珩轮的中心距;φd、φh分别为金刚石修整轮和珩轮的旋转角;Zd、Zh分别为金刚石修整轮和珩轮的齿数;Σ0为金刚石修整轮和珩轮的轴交角。

根据齿轮啮合原理[10],可以得到珩轮和金刚石修整齿轮的啮合方程如下:

(7)

珩轮齿面的位置矢量和法向量可以通过联立(1)～(7)式求解得到。

2 工件实际修形齿面数学模型

内齿珩轮强力珩齿齿向修形运动过程中,C1轴、C2轴、Z1轴、X轴、A轴进行联动,A轴为机床设定参数,附加径向(X轴)运动量由修形量决定。

2.1 附加径向运动量

本文根据修形曲线调整机床运动来实现齿向修形的方式如下:在机床珩削标准齿轮(未修形齿轮)时各轴运动的基础上,通过在机床径向运动(X轴的运动)上添加附加运动,达到修形的目的。不同齿宽位置处的齿向修形量不同,珩轮沿工件齿宽方向进行轴向进给的时候,径向运动轴需要根据齿向修形曲线附加不同的运动量,从而完成整个齿面齿宽方向的修形。附加径向运动量与齿向修形量的关系如图4所示。其中:M为分度圆与渐开线的交点;r、rb分别为工件分度圆半径和基圆半径;黑色虚线为修形前廓形(即标准渐开线);红色实线为修形后廓形。

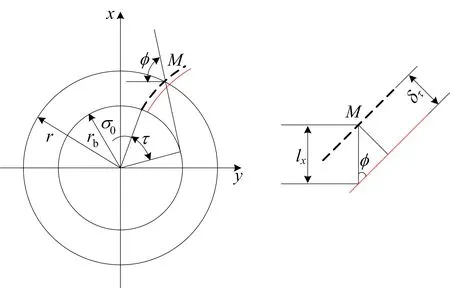
(a) 轮齿端截面 (b) 修形量与附加径向运动量关系图4 修形量与附加运动量关系示意图

附加径向运动量与修形量的关系式为:

(8)

其中:δ为修形量;β为工件分度圆螺旋角;lx为附加径向运动量;σ0为渐开线起始角;τ为渐开线展成角。

2.2 内齿珩轮强力珩齿齿向修形运动模型

根据机床结构和各轴的运动关系,建立内齿珩轮齿向修形加工运动坐标系,如图5所示。

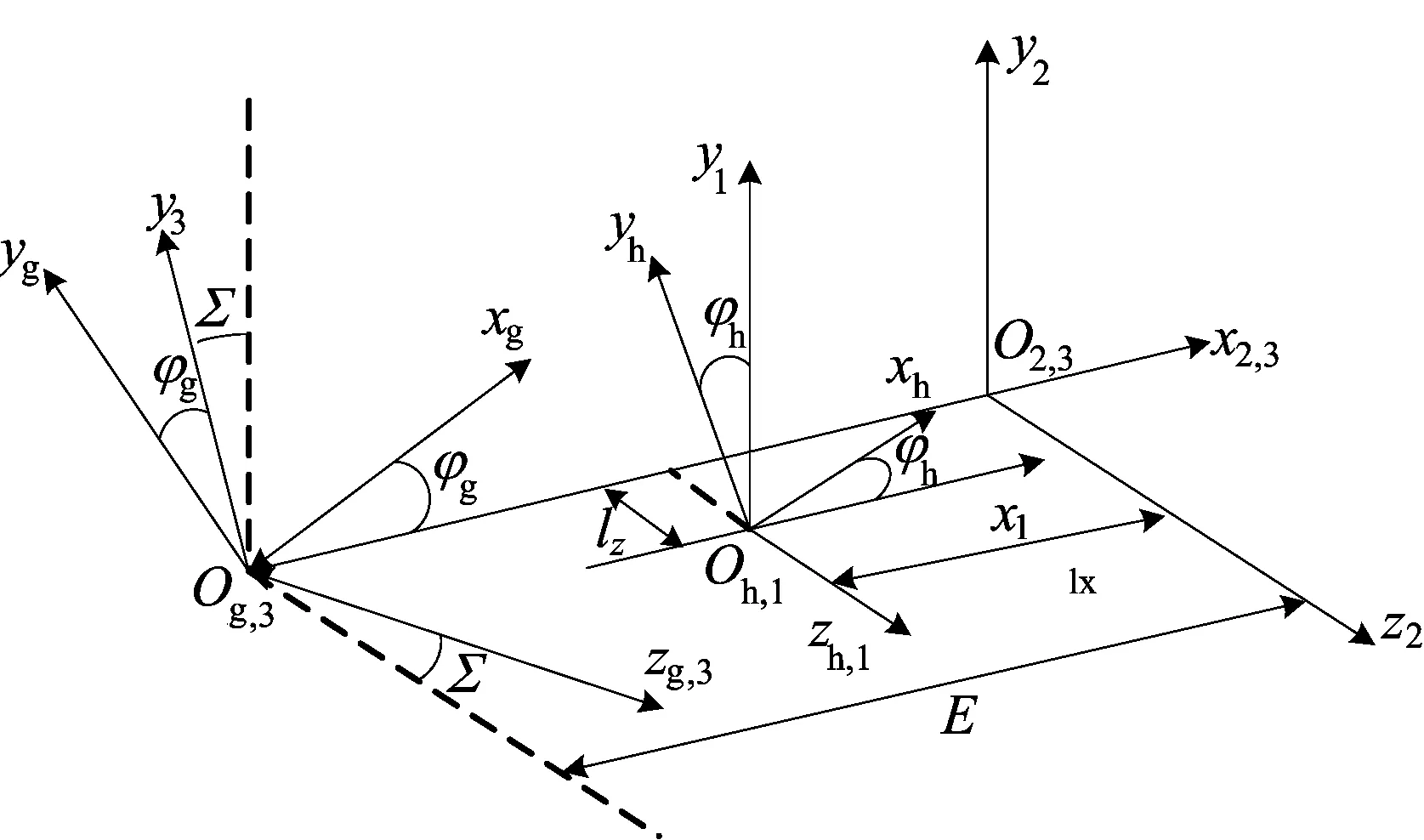
图5 内齿珩轮齿向修形加工运动坐标系

坐标系Sh(Oh-xhyhzh)和Sg(Og-xgygzg)分别固联在珩轮和工件齿轮上,坐标系S1(O1-x1y1z1)、S2(O2-x2y2z2)、S3(O3-x3y3z3)为方便于坐标变换的辅助坐标系;φh、φg分别为珩轮和工件的转角;lz、lx分别为珩轮的轴向位移和径向位移(附加径向运动量);Σ为珩轮与工件的轴交角,坐标系Sh(Oh-xhyhzh)和Sg(Og-xgygzg)的坐标变换矩阵如下:

Mgh=Mg3M32M21M1h

(9)

其中

珩轮在坐标系Sh(Oh-xhyhzh)下的位置矢量和法向量与工件在坐标系Sg(Og-xgygzg)下的位置矢量和法向量的关系式为:

Mgh(lx,lz)rh(λd,θd,φd)

(10)

Lgh(lx,lz)nh(λd,θd,φd)

(11)

由齿轮啮合原理可知,珩轮与工件齿轮在齿向修形过程中的啮合方程为:

(12)

工件转角φg、珩轮转角φh以及珩轮轴向位移lz的联动关系式为:

φg=(Zh/Zg)φh+(tanβg/rg′)lz

(13)

工件齿轮实际修形齿面的位置矢量和法向量可以联立(8)～(13)式求解得到。

3 算例与分析

本文以具体齿轮修形加工为例,对提出的修形方法进行详细的分析。

3.1 算例1

齿向鼓形修形由于设计简单、加工方便且修形效果明显得到了广泛应用。本文以齿向鼓形修形为例,齿向鼓形抛物线修形曲线如图6所示。

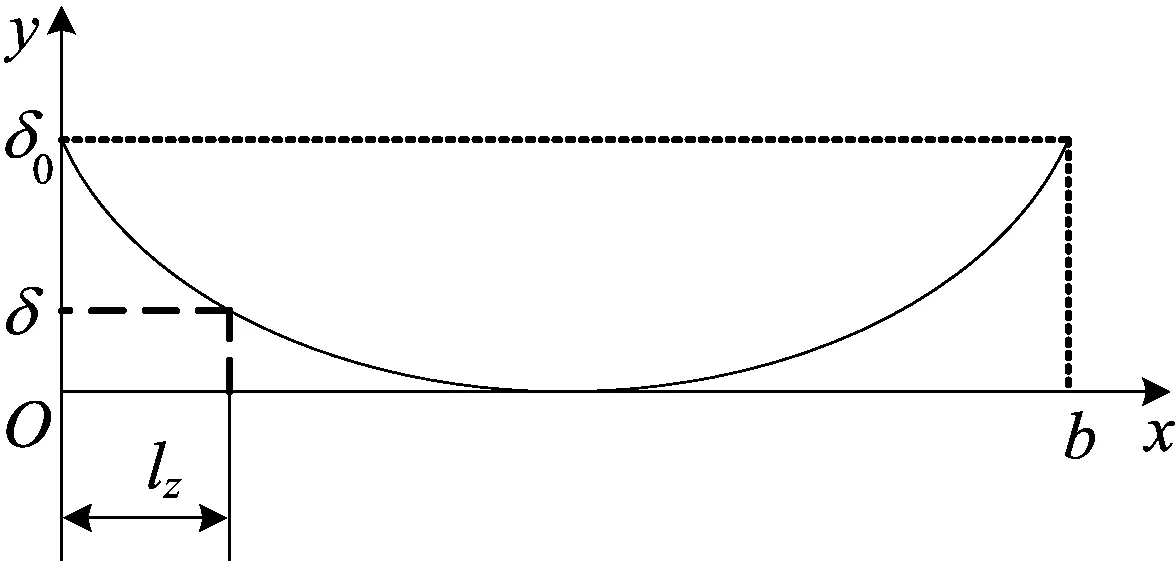
图6 鼓形抛物线修形曲线示意图

修形曲线函数为:

δ=(4δ0/b2)(lz-b/2)2

其中:δ为修形量;lz为珩轮沿齿宽方向位移量;b为齿宽;δ0为鼓形量。

珩轮、金刚石修整轮、工件齿轮的参数见表1所列。

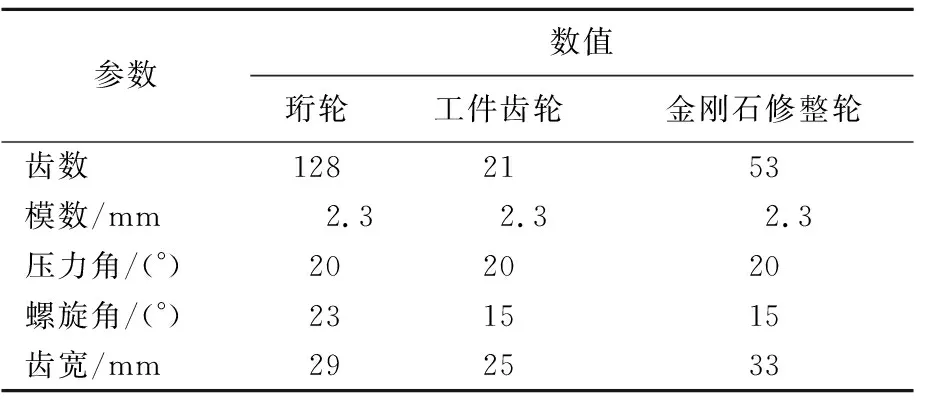
表1 珩轮、工件、金刚石修整轮参数

表1中：鼓形量取30 μm;珩轮、工件、金刚石修整轮旋向均为左旋。

为了直观描述实际修形齿面的形状,将齿面进行网格划分(本文将齿面划分为5×9个网格点)并求解网格点处实际修形齿面与标准齿面的齿面偏差。

将表1参数和修形参数输入实际修形齿面数学模型,并在Matlab中编程求解得到实际修形齿面和标准齿面的齿面偏差,结果见表2、图7所示。图7和表2中:粗实线网格面为实际修形齿面;细实线网格面为标准齿面;网格点间的线段长度表示齿面偏差;字母序号表示齿高方向上不同齿高的位置;数字序号表示齿宽方向上不同端截面的位置。

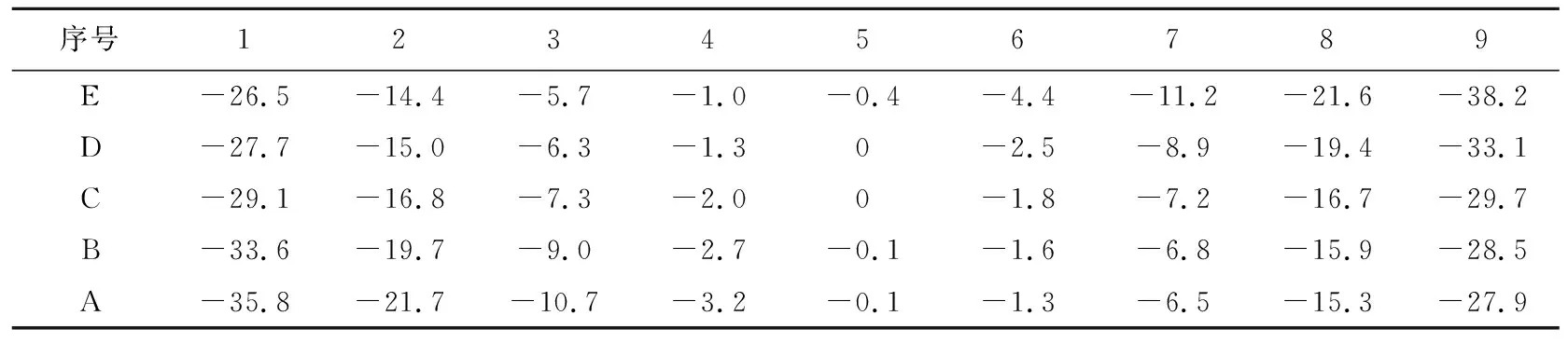
表2 算例1实际修形齿面与标准齿面网格点处齿面偏差值 单位:μm

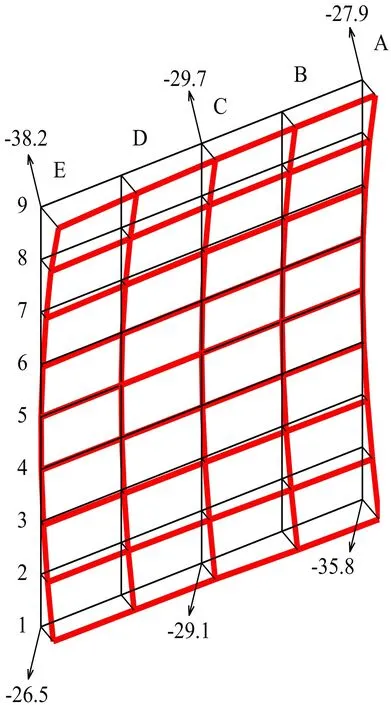
图7 算例1修形齿面与标准齿面的齿面偏差

由表2和图7可知:修形量沿齿宽两端向齿宽中心逐渐递减,在齿宽中心处修形量接近于0,在齿宽两端修形量较大且最大值为38.2 μm;修形后的齿面在齿宽方向上呈鼓状,修形效果明显;实际修形齿面与理论修形齿面存在齿面误差,主要体现为齿面扭曲误差,网格点处齿面误差最大值为8.2 μm,实际修形齿面与理论修形齿面网格点处齿面误差平方和为226.44 μm2,修形精度满足要求。

3.2 算例2

在算例2中采用的修形曲线如图8所示,修形曲线由1条抛物线和2条直线组成。

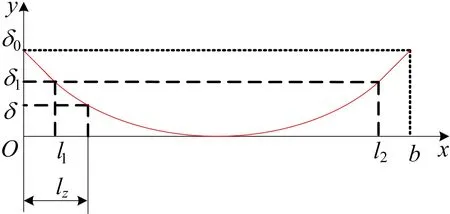
图8 齿向修形曲线示意图

修形曲线的函数为:

其中:δ0=25 μm;δ1=8.33 μm;l1=6.25 mm;l2=18.75 mm;b=25 mm。将各参数输入实际修形齿面数学模型,求解得到实际修形齿面与标准齿面的齿面偏差,结果见表3、图9所示。

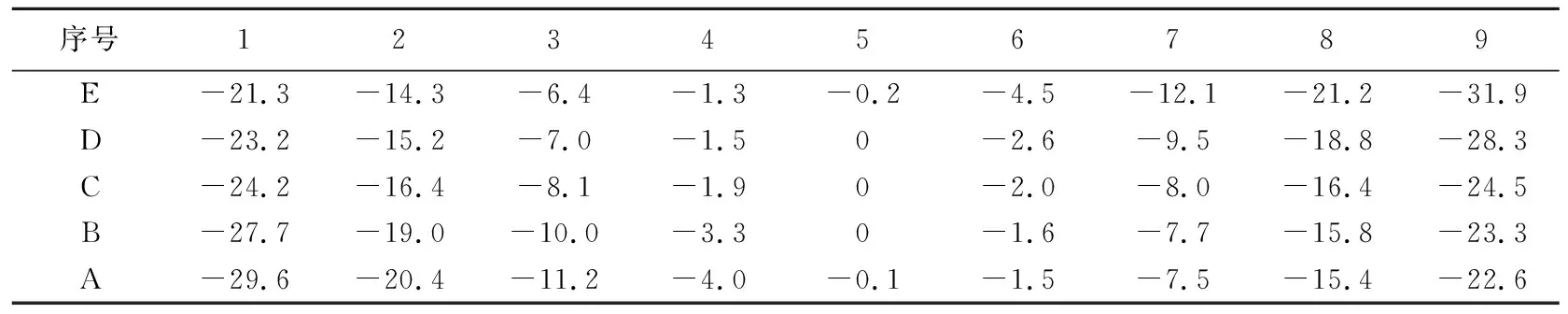
表3 算例2实际修形齿面与标准齿面网格点处齿面偏差值 单位:μm

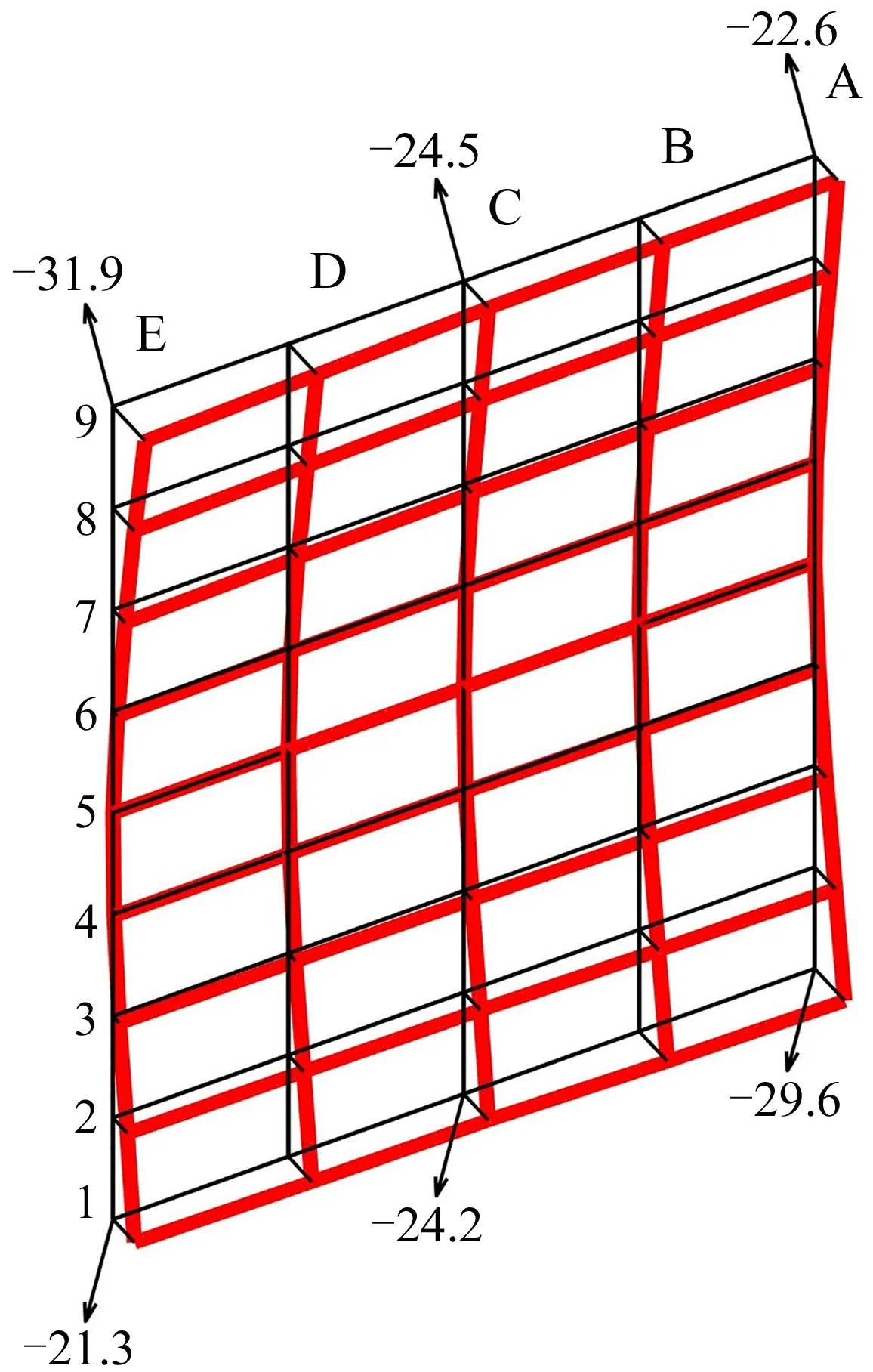
图9 算例2修形齿面与标准齿面的齿面偏差

由表3和图9可知:实际修形齿面最大修形量为31.9 μm,齿面修形效果明显;实际修形齿面与理论修形齿面存在齿面误差,主要体现为齿面扭曲误差,网格点处齿面误差最大值为6.9 μm,实际修形齿面与理论修形齿面网格点处齿面误差平方和为214.13 μm2,修形精度满足要求。

4 结 论

本文提出在珩齿加工过程中的径向运动上添加附加运动,通过多轴联动的方式对齿轮进行齿向修形加工。首先根据金刚石修整轮修整加工机理建立了内齿珩轮齿面数学模型;然后根据珩齿修形加工机理建立了工件实际修形齿面数学模型;最后通过算例对修形效果进行了验证。

根据算例仿真结果可知,利用本文提出的修形方法进行齿向修形加工后,实际修形齿面的修形效果明显,实际修形齿面与理论修形齿面存在齿面误差,主要体现为齿面扭曲误差,算例1和算例2中的实际修形齿面与理论修形齿面的齿面误差最大值分别为8.2 μm和6.9 μm,网格点处实际修形齿面与理论修形齿面的齿面误差平方和分别为226.44 μm2和214.13 μm2,修形精度满足要求。因此利用本文提出的齿向修形方法可以实现对工件齿轮的珩齿修形加工,从而提高金刚石修整轮的通用性。